华师大版 八年级上册 13.2.4角边角 课件(共19张PPT)
文档属性
| 名称 | 华师大版 八年级上册 13.2.4角边角 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 09:56:14 | ||
图片预览






文档简介
(共19张PPT)
角边角
一天,小明的妈妈叫他去玻璃店买一块三角形玻璃,小明不小心把买的三角形玻璃打碎成了三块,他为了省事,他从打碎的三块玻璃中选一块去,小明想法能办得到吗?若能,你认为小明应该拿哪块玻璃去呢?为什么?请同学们小组讨论一下.思考后请同学们回答?
1.边角边公理:
边-角-边(S-A-S)
如果两个三角形有两条边及其夹角分别对应相等,那么这两个三角形全等.
如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?
两种情况:
角-边-角
角-角-边
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等吗?
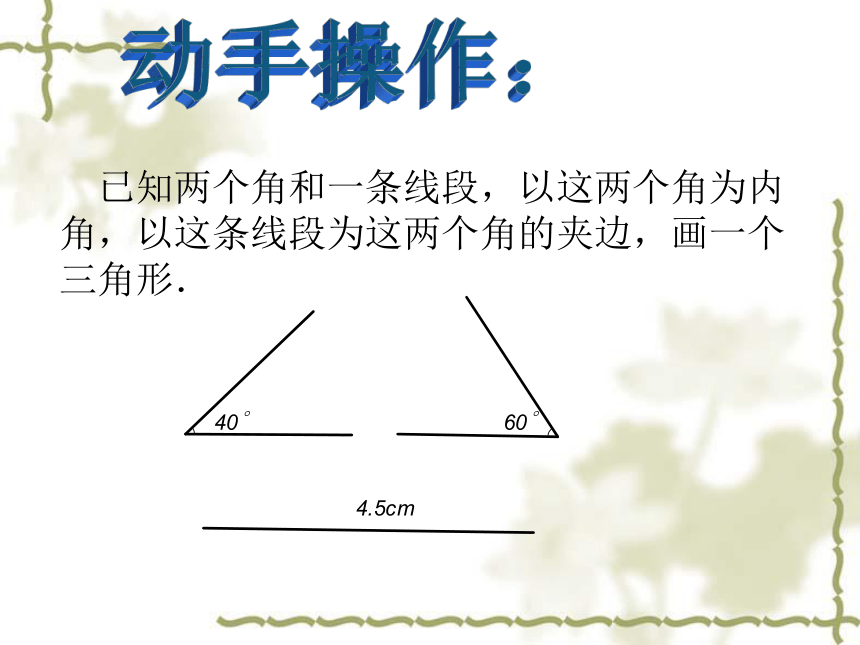
已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.
1.画线段AB,使它等于4.5cm.
2.以A为顶点,AB为一边,画∠MAB=40°.
3.以B为顶点,BA为一边,画∠NBA=60°,交AM于点C.
△ABC即为所求.
如图,在 ABC和 DEF中,已知,BC=EF,∠B=∠E,∠C=∠F. ABC和 DEF能完全重合吗?
D
F
E
A
C
B
( )
( )
( )
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等,简写成:“角边角”或“A.S.A”.
≌
符号语言
一天,小明的妈妈叫他去玻璃店买一块三角形玻璃,小明不小心把买的三角形玻璃打碎成了三块,他为了省事,他从打碎的三块玻璃中选一块去,小明想法能办得到吗?若能,你认为小明应该拿哪块玻璃去呢?为什么?请同学们再次小组讨论一下.思考后请同学们回答?
如图,已知∠ABC=∠DCB, ∠ACB= ∠DBC.
求证:△ABC ≌△DCB.
证明:在△ABC和△DCB中
∴△ABC ≌△DCB(A.S.A)
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
如图,已知∠A=∠A', ∠B= ∠B' ,BC=B' C'
求证:△ABC≌△A'B'C'.
证明:如图∠A=∠A',∠B= ∠B',BC=B' C'
由三角形的内角和等于180度可知:
∴∠C=∠C'.
在△ABC和△A'B'C'中
∴△ABC ≌△A'B'C'(A.S.A)
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形全等,简写: “角角边”或“ A.A.S”.
符号语言
在△ABC和△DEF中
△ABC ≌△DEF(A.A.S)
证明:∵AB=AC
∴∠B=∠C
∵D是BC的中点
∴BD=CD
在 BED和 CFD中
∴ BED ≌ CFD(A.A.S)
∴DE=DF(全等三角形对应边相等)
即BF与AD相等,且互相垂直.
┴
如图.在 ABC中,BC=AC, AC BC,直线EF交AC于点F,交AB于点E,交BC的延长线于点D,且CF=CD,连结AD、BF,则BF与AD有何关系?试证明你的结论.
解:BF与AD相等,且互相垂直.
证明:延长BF交AD与点G
┴
∵AC BC
∴∠BCF=∠ACD=
在 BCF和 ACD中
∴ BCF ≌ ACD(S.A.S)
∴BF=AD,∠CBF=∠DAC
又∵∠BFC=∠AFG
∴∠BCF=∠AGF
又∵∠BCF=
∴∠AGF=
∴BF AD,
G
二、选做题:
1、下列说法中: 如果两个三角形可以依据“A.A.S”来判定全等,那么一定也可以依据“A.S.A”来判断它们全等; 如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等; 要判断两个三角形全等,给出的条件中至少要有一对对应边相等.正确的有( )
A、 B、 C、 D、
2、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF
AE于点F,连接DE,求证:DF=DC.
一、必做题:课本习题19.2 2,3,4题
角边角
一天,小明的妈妈叫他去玻璃店买一块三角形玻璃,小明不小心把买的三角形玻璃打碎成了三块,他为了省事,他从打碎的三块玻璃中选一块去,小明想法能办得到吗?若能,你认为小明应该拿哪块玻璃去呢?为什么?请同学们小组讨论一下.思考后请同学们回答?
1.边角边公理:
边-角-边(S-A-S)
如果两个三角形有两条边及其夹角分别对应相等,那么这两个三角形全等.
如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?
两种情况:
角-边-角
角-角-边
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等吗?
已知两个角和一条线段,以这两个角为内角,以这条线段为这两个角的夹边,画一个三角形.
1.画线段AB,使它等于4.5cm.
2.以A为顶点,AB为一边,画∠MAB=40°.
3.以B为顶点,BA为一边,画∠NBA=60°,交AM于点C.
△ABC即为所求.
如图,在 ABC和 DEF中,已知,BC=EF,∠B=∠E,∠C=∠F. ABC和 DEF能完全重合吗?
D
F
E
A
C
B
( )
( )
( )
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等,简写成:“角边角”或“A.S.A”.
≌
符号语言
一天,小明的妈妈叫他去玻璃店买一块三角形玻璃,小明不小心把买的三角形玻璃打碎成了三块,他为了省事,他从打碎的三块玻璃中选一块去,小明想法能办得到吗?若能,你认为小明应该拿哪块玻璃去呢?为什么?请同学们再次小组讨论一下.思考后请同学们回答?
如图,已知∠ABC=∠DCB, ∠ACB= ∠DBC.
求证:△ABC ≌△DCB.
证明:在△ABC和△DCB中
∴△ABC ≌△DCB(A.S.A)
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
如图,已知∠A=∠A', ∠B= ∠B' ,BC=B' C'
求证:△ABC≌△A'B'C'.
证明:如图∠A=∠A',∠B= ∠B',BC=B' C'
由三角形的内角和等于180度可知:
∴∠C=∠C'.
在△ABC和△A'B'C'中
∴△ABC ≌△A'B'C'(A.S.A)
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形全等,简写: “角角边”或“ A.A.S”.
符号语言
在△ABC和△DEF中
△ABC ≌△DEF(A.A.S)
证明:∵AB=AC
∴∠B=∠C
∵D是BC的中点
∴BD=CD
在 BED和 CFD中
∴ BED ≌ CFD(A.A.S)
∴DE=DF(全等三角形对应边相等)
即BF与AD相等,且互相垂直.
┴
如图.在 ABC中,BC=AC, AC BC,直线EF交AC于点F,交AB于点E,交BC的延长线于点D,且CF=CD,连结AD、BF,则BF与AD有何关系?试证明你的结论.
解:BF与AD相等,且互相垂直.
证明:延长BF交AD与点G
┴
∵AC BC
∴∠BCF=∠ACD=
在 BCF和 ACD中
∴ BCF ≌ ACD(S.A.S)
∴BF=AD,∠CBF=∠DAC
又∵∠BFC=∠AFG
∴∠BCF=∠AGF
又∵∠BCF=
∴∠AGF=
∴BF AD,
G
二、选做题:
1、下列说法中: 如果两个三角形可以依据“A.A.S”来判定全等,那么一定也可以依据“A.S.A”来判断它们全等; 如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等; 要判断两个三角形全等,给出的条件中至少要有一对对应边相等.正确的有( )
A、 B、 C、 D、
2、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF
AE于点F,连接DE,求证:DF=DC.
一、必做题:课本习题19.2 2,3,4题
