21.2.4一元二次方程的根与系数的关系 课件(共17张PPT)
文档属性
| 名称 | 21.2.4一元二次方程的根与系数的关系 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 949.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 15:06:52 | ||
图片预览






文档简介
(共17张PPT)
21.2.4一元二次方程的根与系数的关系
人教版 九年级上册
教学目标
教学目标:
1.掌握根与系数的关系;
2.利用根与系数的关系求方程的解或系数或含方程两根的代数式的值.
重点:掌握根与系数的关系.
难点:利用根与系数的关系求方程的解或系数或含方程两根的代数式的值.
新知导入
1.写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
2.一元二次方程的求根公式:
想一想:方程的两根 x1和 x2与系数a,b,c还有其他关系吗?
新知讲解
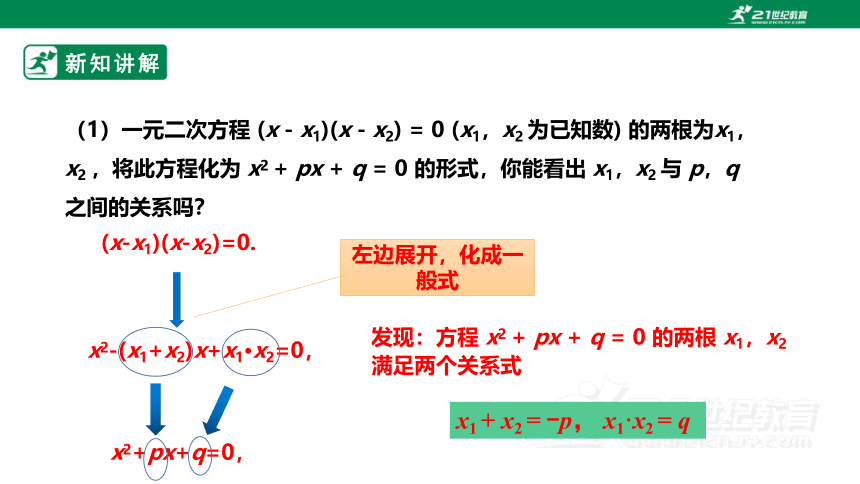
(1)一元二次方程 (x - x1)(x - x2) = 0 (x1,x2 为已知数) 的两根为x1,x2 ,将此方程化为 x2 + px + q = 0 的形式,你能看出 x1,x2 与 p,q 之间的关系吗?
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
左边展开,化成一般式
发现:方程 x2 + px + q = 0 的两根 x1,x2 满足两个关系式
x1 + x2 = -p, x1·x2 = q
新知讲解
一般地,一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1,x2, 两根之和x1+x2、两根之积x1x2 与系数有怎样的关系呢?
根据求根公式可知:
由此可知:
新知讲解
一元二次方程的根与系数的关系
如果 ax2+bx+c=0(a≠0)的两个根为x1、 x2,那么
这表明任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
【特别强调】满足上述关系的前提条件:b2-4ac≥0.
新知讲解
例4 根据一元二次方程的根与系数的关系,求下列方程两个根
x1,x2 的和与积:
(1) x2-6x-15=0 (2)3x2+7x-9=0 (3) 5x-1=4x2
解:(1) a=1,b= -6,c= -15
x1+x2= -(-6)=6,x1x2= -15
(2) a=3,b=7,c= -9
x1+x2= ,x1x2=
(3) 方程可化为 4x2-5x+1=0
a=4,b= -5,c=1
x1+x2= ,x1x2=
针对训练
设 x1,x2 为方程 x2 - 4x + 1 = 0 的两个根,则
(1) x1 + x2 = ; (2) x1·x2 = ;
(3) ; (4) .
4
1
14
12
新知讲解
常见的求值式子如下:
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
课堂练习
1.根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2 的和与积:
(1)x2-6x-15=0
(2)3x2-9+7x=0
(3)5x-1=4x2
x1+x2=6
x1x2=-15
x1+x2=
x1x2=-3
x1+x2=
x1x2=
课堂练习
2.已知一元二次方程x2-6x+c=0有一个根为2,则另一个根为( )
A.2 B.3 C.4 D.8
C
3.一元二次方程x2﹣2x=0的两根分别为x1和x2,则x1x2为( )
A.﹣2 B.1 C.2 D.0
D
课堂练习
5. 如果-1是方程2x2-x+m=0的一个根,则另一个根是___,m =____.
6. 已知一元二次方程x2+px+q=0的两根分别为-2 和 1 ,则:p = , q= .
1
-2
-3
4.若α,β是方程x2-2x-3=0的两个实数根,则α2+β2的值为( )
A.10 B.9 C.7 D.5
A
课堂练习
7. 已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程 5x2+kx-6=0的两个根分别是x1、x2,其中x1=2 .
所以:x1 · x2=2x2=
即:x2=
由于x1+x2=2+ =
得:k=-7.
答:方程的另一个根是 ,k=-7.
课堂练习
8. 设 x1,x2 是方程 3x2 + 4x -3 = 0 的两个根. 利用根与系数之间的关系,求下列各式的值.
(1) (x1 + 1)(x2 + 1); (2)
解:由根与系数的关系,得
(1)(x1 + 1)(x2 + 1) = x1 x2 + x1 + x2 + 1 =
(2)
课堂总结
根与系数的关系
(韦达定理)
内 容
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2= -p ,x1 ·x2=q.
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
应 用
常见变形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
21.2.4一元二次方程的根与系数的关系
人教版 九年级上册
教学目标
教学目标:
1.掌握根与系数的关系;
2.利用根与系数的关系求方程的解或系数或含方程两根的代数式的值.
重点:掌握根与系数的关系.
难点:利用根与系数的关系求方程的解或系数或含方程两根的代数式的值.
新知导入
1.写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
2.一元二次方程的求根公式:
想一想:方程的两根 x1和 x2与系数a,b,c还有其他关系吗?
新知讲解
(1)一元二次方程 (x - x1)(x - x2) = 0 (x1,x2 为已知数) 的两根为x1,x2 ,将此方程化为 x2 + px + q = 0 的形式,你能看出 x1,x2 与 p,q 之间的关系吗?
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2+px+q=0,
左边展开,化成一般式
发现:方程 x2 + px + q = 0 的两根 x1,x2 满足两个关系式
x1 + x2 = -p, x1·x2 = q
新知讲解
一般地,一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1,x2, 两根之和x1+x2、两根之积x1x2 与系数有怎样的关系呢?
根据求根公式可知:
由此可知:
新知讲解
一元二次方程的根与系数的关系
如果 ax2+bx+c=0(a≠0)的两个根为x1、 x2,那么
这表明任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
【特别强调】满足上述关系的前提条件:b2-4ac≥0.
新知讲解
例4 根据一元二次方程的根与系数的关系,求下列方程两个根
x1,x2 的和与积:
(1) x2-6x-15=0 (2)3x2+7x-9=0 (3) 5x-1=4x2
解:(1) a=1,b= -6,c= -15
x1+x2= -(-6)=6,x1x2= -15
(2) a=3,b=7,c= -9
x1+x2= ,x1x2=
(3) 方程可化为 4x2-5x+1=0
a=4,b= -5,c=1
x1+x2= ,x1x2=
针对训练
设 x1,x2 为方程 x2 - 4x + 1 = 0 的两个根,则
(1) x1 + x2 = ; (2) x1·x2 = ;
(3) ; (4) .
4
1
14
12
新知讲解
常见的求值式子如下:
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
课堂练习
1.根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2 的和与积:
(1)x2-6x-15=0
(2)3x2-9+7x=0
(3)5x-1=4x2
x1+x2=6
x1x2=-15
x1+x2=
x1x2=-3
x1+x2=
x1x2=
课堂练习
2.已知一元二次方程x2-6x+c=0有一个根为2,则另一个根为( )
A.2 B.3 C.4 D.8
C
3.一元二次方程x2﹣2x=0的两根分别为x1和x2,则x1x2为( )
A.﹣2 B.1 C.2 D.0
D
课堂练习
5. 如果-1是方程2x2-x+m=0的一个根,则另一个根是___,m =____.
6. 已知一元二次方程x2+px+q=0的两根分别为-2 和 1 ,则:p = , q= .
1
-2
-3
4.若α,β是方程x2-2x-3=0的两个实数根,则α2+β2的值为( )
A.10 B.9 C.7 D.5
A
课堂练习
7. 已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程 5x2+kx-6=0的两个根分别是x1、x2,其中x1=2 .
所以:x1 · x2=2x2=
即:x2=
由于x1+x2=2+ =
得:k=-7.
答:方程的另一个根是 ,k=-7.
课堂练习
8. 设 x1,x2 是方程 3x2 + 4x -3 = 0 的两个根. 利用根与系数之间的关系,求下列各式的值.
(1) (x1 + 1)(x2 + 1); (2)
解:由根与系数的关系,得
(1)(x1 + 1)(x2 + 1) = x1 x2 + x1 + x2 + 1 =
(2)
课堂总结
根与系数的关系
(韦达定理)
内 容
如果方程x2+px+q=0的两根是x1,x2,那么x1+x2= -p ,x1 ·x2=q.
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
应 用
常见变形
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
