沪科版数学八年级上册同步提优训练:12.4 综合与实践 一次函数模型的应用(word版含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步提优训练:12.4 综合与实践 一次函数模型的应用(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 10:36:45 | ||
图片预览


文档简介
12.4 综合与实践 一次函数模型的应用
考向题组训练
命题点 1 构建一次函数模型求表达式
1.王明妈妈购进一批苹果,到售货市场零售,已知卖出的苹果质量x(千克)与售价y(元)之间的对应关系如图下表所示:
质量(千克) 1 2 3 4 5
售价(元) 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5
则y关于x的函数表达式为 ( )
A.y=2x+0.1 B.y=2x+0.1x
C.y=4x+0.2 D.y=4x+0.2x
2.某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路,若平均每天的修建费y(万元)与修建天数x(天)在30≤x≤120范围内具有一次函数关系,部分对应值如图下表所示:
x(天) 50 60 90 120
y(万元) 40 38 32 26
则y关于x的函数表达式为 .
3.是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为x cm,双层部分的长度为y cm,经测量,得到如图下数据:
单层部分的 长度x (cm) … 100 90 80 50 …
双层部分的 长度y (cm) … 15 20 25 35 …
(1)根据表中数据的规律,完成表格,并直接写出y关于x的函数表达式;
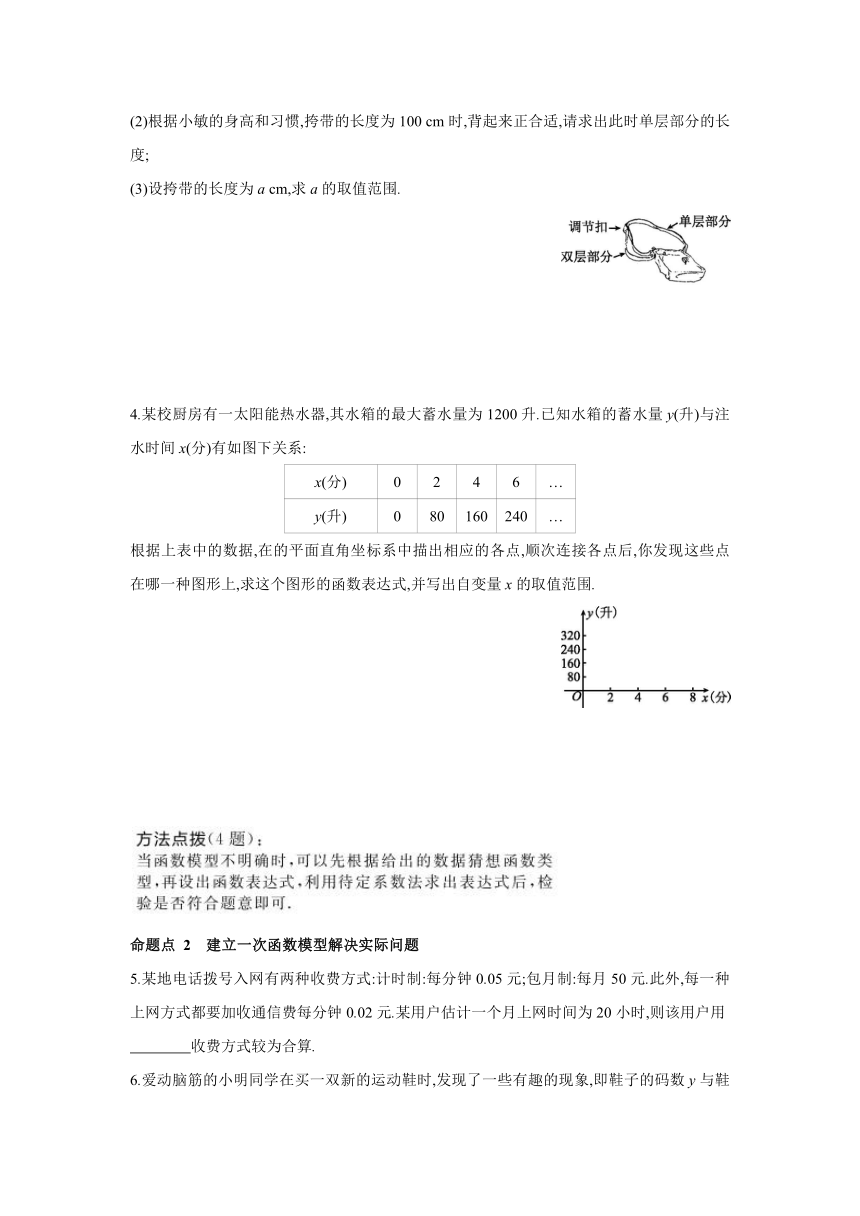
(2)根据小敏的身高和习惯,挎带的长度为100 cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为a cm,求a的取值范围.
4.某校厨房有一太阳能热水器,其水箱的最大蓄水量为1200升.已知水箱的蓄水量y(升)与注水时间x(分)有如图下关系:
x(分) 0 2 4 6 …
y(升) 0 80 160 240 …
根据上表中的数据,在的平面直角坐标系中描出相应的各点,顺次连接各点后,你发现这些点在哪一种图形上,求这个图形的函数表达式,并写出自变量x的取值范围.
命题点 2 建立一次函数模型解决实际问题
5.某地电话拨号入网有两种收费方式:计时制:每分钟0.05元;包月制:每月50元.此外,每一种上网方式都要加收通信费每分钟0.02元.某用户估计一个月上网时间为20小时,则该用户用
收费方式较为合算.
6.爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣的现象,即鞋子的码数y与鞋子的长度x(cm)之间存在着某种联系,经过收集数据,得到下表:
鞋长x(cm) … 22 23 24 25 26 …
码数y … 34 36 38 40 42 …
请你帮小明解决下列问题:
(1)根据表中数据,在同一平面直角坐标系中描出相应的点,你发现这些点在哪一种图形上
(2)猜想y与x之间满足怎样的函数关系,并求出y与x之间的函数表达式,验证这些点的坐标是否满足函数表达式;
(3)当鞋码是41码时,鞋长是多少
思维拓展培优
7.为提醒人们节约用水,及时修好漏水的水龙头,两名同学分别做了水龙头漏水试验,他们用于接水的量筒最大容量为100毫升.
试验一:小王同学在做水龙头漏水试验时,每隔10秒观察量筒中水的体积,记录的数据如图下表(漏出的水量精确到1毫升):
时间t(秒) 10 20 30 40 50 60 70
漏出水量V(毫升) 2 5 8 11 14 17 20
(1)在①的平面直角坐标系中描出上表中数据对应的点;
(2)如图果小王同学继续试验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)
(3)按此漏水速度,一小时会漏水 升(精确到0.1升)
试验二:小李同学根据自己的试验数据画出的图象如图图②所示,为什么图象中会出现与横轴“平行”的部分
答案
12.4 综合与实践 一次函数模型的应用
1.B 从表格可以看出:
质量为1千克时,售价为(2×1+0.1×1)元,
质量为2千克时,售价为(2×2+0.1×2)元,
质量为3千克时,售价为(2×3+0.1×3)元,
……
根据变化规律可知y=2x+0.1x.故选B.
2.y=-x+50(30≤x≤120) 设y关于x的函数表达式为y=kx+b,则
解得
所以y=-x+50.故y关于x的函数表达式为y=-x+50(30≤x≤120).
3.解:(1)观察表格中数据可知,y是x的一次函数,设y=kx+b,
则有
解得
所以y=-x+65.
当y=35时,x=60;当x=50时,y=40.
故表中从上往下依次填60,40,y关于x的函数表达式为y=-x+65.
(2)由题意,得x+y=100,即x+-x+65=100,解得x=70.
答:单层部分的长度为70 cm.
(3)因为当y=0时,x=130,当x=0时,y=65,
所以65≤a≤130.
4.解:描点连线如图图,发现四个点在经过原点的一条直线上.设这个图形的函数表达式为y=kx(k≠0).
将x=2,y=80代入y=kx(k≠0)中,得80=2k,解得k=40,所以y=40x.
把x=4,y=160代入所得的函数表达式,左边=160,右边=40×4=160,因此左边=右边,即点(4,160)满足该函数的表达式.
同理可验证(6,240)也满足该函数的表达式.
因此这个图形的函数表达式是y=40x,x的取值范围是0≤x≤30.
5.包月制 设上网时间为x小时,所付费用为y元.根据题意,得用计时制所需费用y=(0.05+0.02)·60x=4.2x;用包月制所需费用y=50+0.02·60x=50+1.2x.当x=20时,用计时制费用为4.2×20=84(元);用包月制费用为50+1.2×20=74(元),所以该用户采用包月制较为合算.
6.解: (1)如图图,描点后可发现这些点近似在一条直线上.
(2)猜想y与x之间满足一次函数关系.
设y=kx+b(k≠0),把(22,34),(23,36)代入,得解得
所以y=2x-10.
验证:当x=24时,y=2×24-10=38;
当x=25时,y=2×25-10=40;
当x=26时,y=2×26-10=42.
所以这些点的坐标都满足这个函数表达式.
(3)当y=41时,有2x-10=41,解得x=25.5,即鞋码是41码时,鞋长是25.5 cm.
7.解: 试验一:(1)描点如图图所示.
(2)由(1)中的图象可知V与t之间满足一次函数关系.
设V与t之间的函数表达式为V=kt+b.
根据表中数据知:当t=10时,V=2;当t=20时,V=5.
所以解得
所以V与t之间的函数表达式为V=t-1.
由题意,得t-1≥100,
解得t≥=336≈337.
所以337秒后量筒中的水会满而溢出.
(3)1.1
试验二:因为小李同学接水的量筒装满后开始溢出,量筒内的水位不再发生变化,所以图象中会出现与横轴“平行”的部分.
考向题组训练
命题点 1 构建一次函数模型求表达式
1.王明妈妈购进一批苹果,到售货市场零售,已知卖出的苹果质量x(千克)与售价y(元)之间的对应关系如图下表所示:
质量(千克) 1 2 3 4 5
售价(元) 2+0.1 4+0.2 6+0.3 8+0.4 10+0.5
则y关于x的函数表达式为 ( )
A.y=2x+0.1 B.y=2x+0.1x
C.y=4x+0.2 D.y=4x+0.2x
2.某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路,若平均每天的修建费y(万元)与修建天数x(天)在30≤x≤120范围内具有一次函数关系,部分对应值如图下表所示:
x(天) 50 60 90 120
y(万元) 40 38 32 26
则y关于x的函数表达式为 .
3.是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为x cm,双层部分的长度为y cm,经测量,得到如图下数据:
单层部分的 长度x (cm) … 100 90 80 50 …
双层部分的 长度y (cm) … 15 20 25 35 …
(1)根据表中数据的规律,完成表格,并直接写出y关于x的函数表达式;
(2)根据小敏的身高和习惯,挎带的长度为100 cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为a cm,求a的取值范围.
4.某校厨房有一太阳能热水器,其水箱的最大蓄水量为1200升.已知水箱的蓄水量y(升)与注水时间x(分)有如图下关系:
x(分) 0 2 4 6 …
y(升) 0 80 160 240 …
根据上表中的数据,在的平面直角坐标系中描出相应的各点,顺次连接各点后,你发现这些点在哪一种图形上,求这个图形的函数表达式,并写出自变量x的取值范围.
命题点 2 建立一次函数模型解决实际问题
5.某地电话拨号入网有两种收费方式:计时制:每分钟0.05元;包月制:每月50元.此外,每一种上网方式都要加收通信费每分钟0.02元.某用户估计一个月上网时间为20小时,则该用户用
收费方式较为合算.
6.爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣的现象,即鞋子的码数y与鞋子的长度x(cm)之间存在着某种联系,经过收集数据,得到下表:
鞋长x(cm) … 22 23 24 25 26 …
码数y … 34 36 38 40 42 …
请你帮小明解决下列问题:
(1)根据表中数据,在同一平面直角坐标系中描出相应的点,你发现这些点在哪一种图形上
(2)猜想y与x之间满足怎样的函数关系,并求出y与x之间的函数表达式,验证这些点的坐标是否满足函数表达式;
(3)当鞋码是41码时,鞋长是多少
思维拓展培优
7.为提醒人们节约用水,及时修好漏水的水龙头,两名同学分别做了水龙头漏水试验,他们用于接水的量筒最大容量为100毫升.
试验一:小王同学在做水龙头漏水试验时,每隔10秒观察量筒中水的体积,记录的数据如图下表(漏出的水量精确到1毫升):
时间t(秒) 10 20 30 40 50 60 70
漏出水量V(毫升) 2 5 8 11 14 17 20
(1)在①的平面直角坐标系中描出上表中数据对应的点;
(2)如图果小王同学继续试验,请探求多少秒后量筒中的水会满而溢出(精确到1秒)
(3)按此漏水速度,一小时会漏水 升(精确到0.1升)
试验二:小李同学根据自己的试验数据画出的图象如图图②所示,为什么图象中会出现与横轴“平行”的部分
答案
12.4 综合与实践 一次函数模型的应用
1.B 从表格可以看出:
质量为1千克时,售价为(2×1+0.1×1)元,
质量为2千克时,售价为(2×2+0.1×2)元,
质量为3千克时,售价为(2×3+0.1×3)元,
……
根据变化规律可知y=2x+0.1x.故选B.
2.y=-x+50(30≤x≤120) 设y关于x的函数表达式为y=kx+b,则
解得
所以y=-x+50.故y关于x的函数表达式为y=-x+50(30≤x≤120).
3.解:(1)观察表格中数据可知,y是x的一次函数,设y=kx+b,
则有
解得
所以y=-x+65.
当y=35时,x=60;当x=50时,y=40.
故表中从上往下依次填60,40,y关于x的函数表达式为y=-x+65.
(2)由题意,得x+y=100,即x+-x+65=100,解得x=70.
答:单层部分的长度为70 cm.
(3)因为当y=0时,x=130,当x=0时,y=65,
所以65≤a≤130.
4.解:描点连线如图图,发现四个点在经过原点的一条直线上.设这个图形的函数表达式为y=kx(k≠0).
将x=2,y=80代入y=kx(k≠0)中,得80=2k,解得k=40,所以y=40x.
把x=4,y=160代入所得的函数表达式,左边=160,右边=40×4=160,因此左边=右边,即点(4,160)满足该函数的表达式.
同理可验证(6,240)也满足该函数的表达式.
因此这个图形的函数表达式是y=40x,x的取值范围是0≤x≤30.
5.包月制 设上网时间为x小时,所付费用为y元.根据题意,得用计时制所需费用y=(0.05+0.02)·60x=4.2x;用包月制所需费用y=50+0.02·60x=50+1.2x.当x=20时,用计时制费用为4.2×20=84(元);用包月制费用为50+1.2×20=74(元),所以该用户采用包月制较为合算.
6.解: (1)如图图,描点后可发现这些点近似在一条直线上.
(2)猜想y与x之间满足一次函数关系.
设y=kx+b(k≠0),把(22,34),(23,36)代入,得解得
所以y=2x-10.
验证:当x=24时,y=2×24-10=38;
当x=25时,y=2×25-10=40;
当x=26时,y=2×26-10=42.
所以这些点的坐标都满足这个函数表达式.
(3)当y=41时,有2x-10=41,解得x=25.5,即鞋码是41码时,鞋长是25.5 cm.
7.解: 试验一:(1)描点如图图所示.
(2)由(1)中的图象可知V与t之间满足一次函数关系.
设V与t之间的函数表达式为V=kt+b.
根据表中数据知:当t=10时,V=2;当t=20时,V=5.
所以解得
所以V与t之间的函数表达式为V=t-1.
由题意,得t-1≥100,
解得t≥=336≈337.
所以337秒后量筒中的水会满而溢出.
(3)1.1
试验二:因为小李同学接水的量筒装满后开始溢出,量筒内的水位不再发生变化,所以图象中会出现与横轴“平行”的部分.
