沪科版数学八年级上册同步提优训练:第14章 全等三角形 综合提升卷(word、含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步提优训练:第14章 全等三角形 综合提升卷(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 12:34:00 | ||
图片预览




文档简介
第14章综合提升卷
[时间:120分钟 分值:150分]
第Ⅰ卷 (选择题 共40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.全等三角形是 ( )
A.面积和周长相等的两个三角形
B.形状相同的两个三角形
C.能够完全重合的两个三角形
D.三个角对应相等的两个三角形
2.在建筑工地上我们经常看见如图所示用木条EF固定长方形门框ABCD的情形,
这种做法的根据是 ( )
A.两点之间线段最短
B.两点确定一条直线
C.三角形的稳定性
D.长方形的四个角都是直角
3.在平面直角坐标系内,O为坐标原点,A(-4,0),B(0,3).若在该坐标平面内有一个以P(不与点A,B,O重合)为一个顶点的直角三角形与Rt△ABO全等,且这个以P为一个顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的三角形的个数为 ( )
A.9 B.7 C.5 D.3
4.四个角分别相等,四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A'B'C'D'中,AB=A'B',BC=B'C',CD=C'D'.要使四边形ABCD≌四边形A'B'C'D',可以添加的条件是 ( )
A.DA=D'A' B.∠B=∠B'
C.∠B=∠B',∠C=∠C' D.∠B=∠B',∠D=∠D'
5.是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为 ( )
A.45 cm B.48 cm C.51 cm D.54 cm
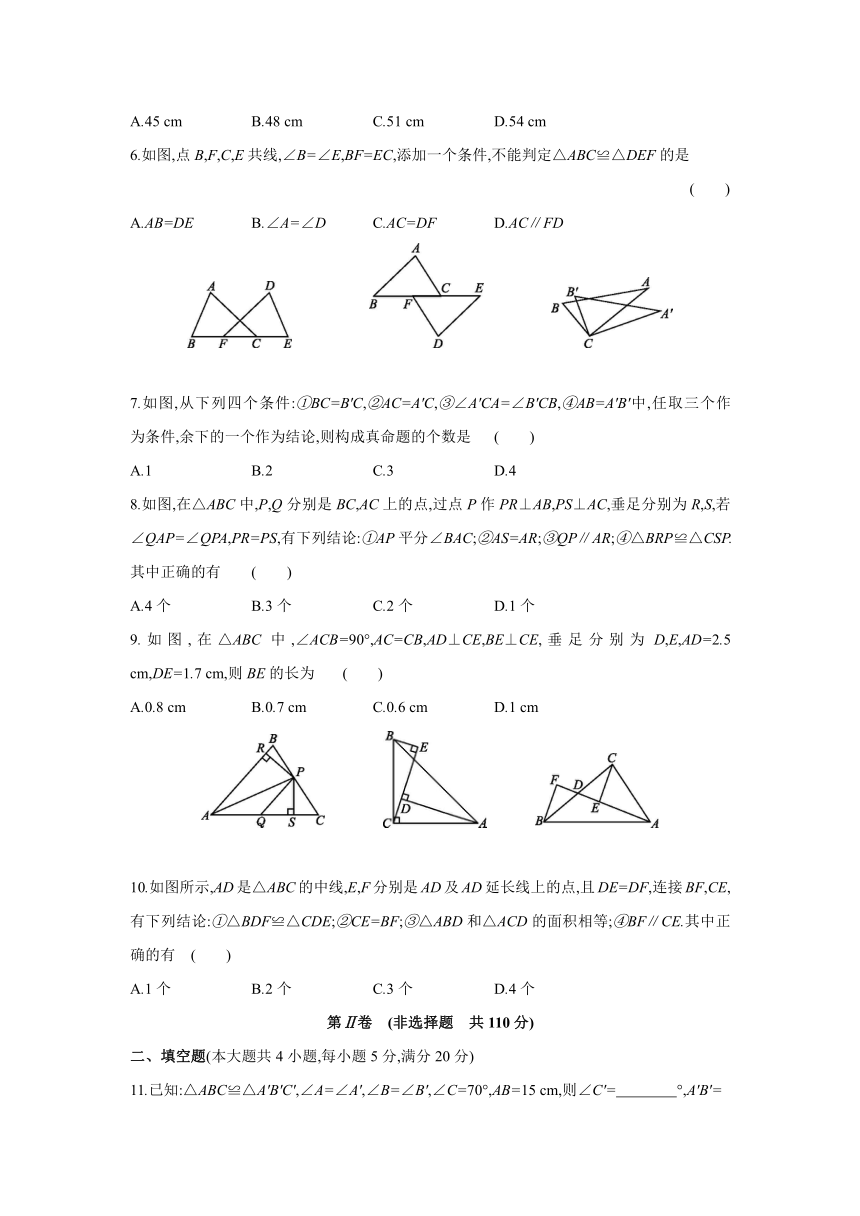
6.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是
( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
7.如图,从下列四个条件:①BC=B'C,②AC=A'C,③∠A'CA=∠B'CB,④AB=A'B'中,任取三个作为条件,余下的一个作为结论,则构成真命题的个数是 ( )
A.1 B.2 C.3 D.4
8.如图,在△ABC中,P,Q分别是BC,AC上的点,过点P作PR⊥AB,PS⊥AC,垂足分别为R,S,若∠QAP=∠QPA,PR=PS,有下列结论:①AP平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
9.如图,在△ABC中,∠ACB=90°,AC=CB,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5 cm,DE=1.7 cm,则BE的长为 ( )
A.0.8 cm B.0.7 cm C.0.6 cm D.1 cm
10.如图所示,AD是△ABC的中线,E,F分别是AD及AD延长线上的点,且DE=DF,连接BF,CE,有下列结论:①△BDF≌△CDE;②CE=BF;③△ABD和△ACD的面积相等;④BF∥CE.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷 (非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知:△ABC≌△A'B'C',∠A=∠A',∠B=∠B',∠C=70°,AB=15 cm,则∠C'= °,A'B'=
cm.
12.如图,AB=12 cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4 cm,点P从点B向点A运动,每分钟走1 cm,点Q从点B向点D运动,每分钟走2 cm,P,Q两点同时出发,运动 min后△CAP与△PBQ全等.
13.如图,点A在直线l1:y=-3x上,点B在经过原点O的直线l2上,如图果点A的纵坐标与点B的横坐标相等,且OA=OB,那么直线l2的函数表达式是 .
14.如图,在△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm.点P从点A出发沿AC路径向终点C运动,点Q从点B出发沿BCA路径向终点A运动.点P,Q分别以1 cm/s和2 cm/s的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,则点P运动 s时,△PEC≌△QFC.
三、解答题(本大题共2小题,每小题8分,满分16分)
15.已知:如图,点D,E分别在AB,AC上,且AB=AC,添加一个条件,使△AEB≌△ADC,并写出证明过程.
16.如图,为了测量湖宽AB,先在AB的延长线上选定点C,再选一适当的点M,然后延长BM,CM到点B',C',使MB'=MB,MC'=MC.又在C'B'的延长线上找一点A',使A',M,A三点在同一直线上,这时,只要测出线段A'B'的长度就可以知道湖宽,你能说明其中的道理吗
四、解答题(本大题共2小题,每小题8分,满分16分)
17.如图所示,在△ABC中,点A的坐标为(0,1),点C的坐标为(4,3).如图果要使△ABD与△ABC全等,求点D的坐标.
18.如图所示,在△ABC中,AB=AC,∠1=∠2,AD⊥CD于点D,AE⊥BE于点E,BE,CD交于点O.
求证:(1)△ADC≌△AEB;
(2)OD=OE.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.如图,AD=CB,E,F是AC上的两个动点(不与点A,C重合),且有DE=BF.
(1)若点E,F运动至如图图①所示的位置,且AF=CE.求证:△ADE≌△CBF;
(2)若点E,F运动至如图图②所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗 为什么
(3)在(1)(2)的条件下,AD和CB平行吗 请说明理由.
20.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,点D在线段AB上,AD=AC,AF平分∠CAE交CE于点F.
(1)求证:FD∥CB;
(2)如图图②,若点D在线段BA的延长线上,AF是∠CAD的平分线AM的反向延长线,其他条件不变,(1)中的结论是否仍然成立 并说明理由.
六、解答题(本题12分)
21.如图,已知Rt△ABC≌Rt△DBE,∠ACB=∠DEB=90°.
(1)将两三角形按图①所示方式摆放,其中点E落在AB上,DE所在直线交边AC于点F.求证:AF+EF=DE.
(2)若将两三角形按照图②所示方式摆放,边AC的延长线与DE相交于点F.你认为(1)中的结论还成立吗 若成立,写出证明过程;若不成立,请写出AF,EF与DE之间的数量关系,并说明理由.
七、解答题(本题12分)
22.问题情境:如图①,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,可知∠BAD=∠C(不需要证明).
(1)特例探究:如图图②,∠MAN=90°,射线AE在这个角的内部,点B,C分别在∠MAN的边AM,AN上,且AB=CA,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)归纳证明:如图图③,点B,C分别在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角,已知AB=CA,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图图④,在△ABC中,AB=CA,AB>BC.点D在边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .
八、解答题(本题14分)
23.如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a,b满足|a+b|+(a-5)2=0.
(1)点A的坐标为 ,点B的坐标为 ;
(2)如图图①,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE的延长线于点D,试求点D的坐标;
(3)如图图②,M,N分别为OA,OB边上的点,OM=ON,OP⊥AN,过点P作PG⊥BM交AN的延长线于点G,请写出线段AG,OP与PG之间的数量关系,并证明你的结论.(提示:有两个角相等的三角形是等腰三角形,即“等角对等边”)
答案
第14章综合提升卷
1.C A项,面积和周长相等的两个三角形不一定全等,故此选项错误;
B项,形状相同的两个三角形不一定全等,故此选项错误;
C项,能够完全重合的两个三角形一定全等,故此选项正确;
D项,三个角对应相等的两个三角形不一定全等,故此选项错误.故选C.
2.C
3.A 分别以OA,OB,AB为公共边作与Rt△ABO全等的三角形各有3个,则所有符合条件的三角形个数为9.故选A.
4.C 添加的条件是∠B=∠B',∠C=∠C'.如图图,连接AC,A'C',
在△ABC和△A'B'C'中,∵
∴△ABC≌△A'B'C',(SAS)
∴∠ACB=∠A'C'B',∠BAC=∠B'A'C',AC=A'C'.
∵∠BCD=∠B'C'D',
∴∠ACD=∠A'C'D'.
在△ACD和△A'C'D'中,
∵
∴△ACD≌△A'C'D',(SAS)
∴∠D=∠D',AD=A'D',∠DAC=∠D'A'C',
∴∠BAD=∠B'A'D',
∴四边形ABCD≌四边形A'B'C'D'.
故选C.
5.A ∵BF=EC,BC=BF+CF,EF=EC+CF,∴BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),∴C△DEF=C△ABC=24 cm.
∵CF=3 cm,∴制成整个金属框架所需这种材料的总长度为C△DEF+C△ABC-CF=24+24-3=45(cm).故选A.
6.C
7.B 当①②③为条件,④为结论时:∵∠A'CA=∠B'CB,∴∠ACB=∠A'CB'.又∵BC=B'C,AC=A'C,∴△ACB≌△A'CB',∴AB=A'B';当①②④为条件,③为结论时:∵BC=B'C,AC=A'C,AB=A'B',∴△ACB≌△A'CB',∴∠A'CB'=∠ACB,∴∠A'CA=∠B'CB.故选B.
8.B ①∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴Rt△APR≌Rt△APS,∴∠PAR=∠PAS,∴AP平分∠BAC;
②由△APR≌△APS,可得AS=AR;
③∵∠PAR=∠QAP,∠QAP=∠QPA,
∴∠QPA=∠PAR,∴QP∥AR;
④∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP.
∵PR=PS,BR不一定等于CS,∴△BRP不一定与△CSP全等(只具备一角一边的两三角形不一定全等).故选B.
9.A ∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.
∵∠BCE+∠DCA=90°,∴∠EBC=∠DCA.
在△CEB和△ADC中,∵
∴△CEB≌△ADC,(AAS)
∴BE=CD,CE=AD=2.5 cm.
∵CD=CE-DE,DE=1.7 cm,
∴CD=2.5-1.7=0.8(cm),
∴BE=0.8 cm.故选A.
10.D ①∵AD是△ABC的中线,∴BD=CD.
在△BDF和△CDE中,∵
∴△BDF≌△CDE;
②∵△BDF≌△CDE,∴CE=BF;
③∵AD是△ABC的中线,∴S△ABD=S△ACD;
④∵△BDF≌△CDE,∴∠CED=∠BFD,
∴BF∥CE.故选D.
11.70 15 全等三角形的对应边相等,对应角相等.
12.4 ∵CA⊥AB于点A,DB⊥AB于点B,∴∠A=∠B=90°.设运动x min后△CAP与△PBQ全等,则BP=x cm,BQ=2x cm,则AP=(12-x)cm,分两种情况:①若BP=AC,则x=4,AP=12-4=8(cm),BQ=8 cm,AP=BQ,∴△CAP≌△PBQ;②若BP=AP,则12-x=x,解得x=6,BQ=12≠AC,此时△CAP与△PBQ不全等.
综上所述,运动4 min后△CAP与△PBQ全等.
故答案为4.
13.y=x 如图图,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D.
∵点A的纵坐标与点B的横坐标相等,
∴OC=OD.
在Rt△AOC与Rt△BOD中,∵
∴Rt△AOC≌Rt△BOD,
∴AC=BD.
∵点A在直线l1:y=-3x上,
∴设A(-m,3m),
∴AC=BD=m,OD=OC=3m,
∴B(3m,m).
设直线l2的函数表达式为y=kx,
将B(3m,m)代入,得3mk=m,
∴k=,
∴直线l2的函数表达式为y=x.
14.2或 当△PEC≌△QFC时,则有PC=QC.
分两种情况:
①当点Q在线段BC上时,有8-2t=6-t,解得t=2;②当点Q在线段AC上时,2t-8=6-t,解得t=.故答案为2或.
15.解:本题答案不唯一,如图添加AE=AD.证明如图下:
在△AEB和△ADC中,
∵∴△AEB≌△ADC.(SAS)
16.解:在△MBC与△MB'C'中,
∵
∴△MBC≌△MB'C',(SAS)
∴∠MBC=∠MB'C',
∴∠MBA=∠MB'A'.
在△MBA与△MB'A'中,
∵
∴△MBA≌△MB'A',(ASA)∴AB=A'B'.
即只要测出线段A'B'的长度就可以知道湖宽.
17.解:如图图所示,点D的坐标是(-1,3)或(-1,-1)或(4,-1).
18.证明:(1)∵AD⊥DC,AE⊥BE,
∴∠ADC=∠AEB=90°.
∵∠DAC=∠DAE+∠2,∠EAB=∠DAE+∠1,
且∠1=∠2,∴∠DAC=∠EAB.
在△ADC 与△AEB中,
∵
∴△ADC≌△AEB.(AAS)
(2)如图图,连接AO.
∵△ADC≌△AEB,∴AD=AE.
在Rt△ADO和Rt△AEO中,
∵
∴Rt△ADO≌Rt△AEO,(HL)
∴OD=OE.
19.解:(1)证明:∵AF=CE,
∴AF+EF=CE+EF,即AE=CF.
在△ADE和△CBF中,∵
∴△ADE≌△CBF.(SSS)
(2)△ADE≌△CBF仍成立.
理由:∵AF=CE,
∴AF-EF=CE-EF,即AE=CF.
在△ADE和△CBF中,
∵
∴△ADE≌△CBF.(SSS)
(3)AD∥CB.
理由:∵△ADE≌△CBF,∴∠A=∠C,
∴AD∥CB.
20.解:(1)证明:∵AF平分∠CAE,
∴∠DAF=∠CAF.
在△DAF和△CAF中,
∵
∴△DAF≌△CAF,(SAS)
∴∠ACE=∠ADF.
∵∠ACE+∠ECB=90°,∠B+∠ECB=90°,
∴∠B=∠ACE,
∴∠ADF=∠B,∴FD∥CB.
(2)成立.理由:同(1)可证△DAF≌△CAF,
∴∠D=∠ACF.
∵CE⊥AB,∴∠D+∠DFE=90°.
又∵∠ACF+∠FCB=90°,
∴∠DFE=∠FCB,
∴FD∥CB.
21.解:由Rt△ABC≌Rt△DBE,知BC=BE,AC=DE.
(1)证明:如图图①,连接BF.
在Rt△BCF和Rt△BEF中,
∵∴Rt△BCF≌Rt△BEF,(HL)
∴CF=EF.
∵AC=DE,AF+CF=AC,
∴AF+EF=DE.
(2)(1)中的结论不成立,关系为AF=EF+DE.
理由:如图图②,连接BF.
在Rt△BEF和Rt△BCF中,
∵
∴Rt△BEF≌Rt△BCF,(HL)
∴EF=CF.
∵AC=DE,AF=CF+AC,
∴AF=EF+DE.
22.解:(1)证明:∵CF⊥AE,BD⊥AE,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°.
∵∠MAN=90°,∴∠BAD+∠CAF=90°,
∴∠ABD=∠CAF.
在△ABD和△CAF中,∵
∴△ABD≌△CAF.(AAS)
(2)证明:∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠ACF+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠ACF.
在△ABE和△CAF中,∵
∴△ABE≌△CAF.(ASA)
(3)∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是×15=5.
同(3)可证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积.
故答案为5.
23.解:(1)∵|a+b|+(a-5)2=0,∴a=5,b=-5,
∴点A的坐标为(5,0),点B的坐标为(0,-5).
(2)如图图①,过点C作CK⊥x轴于点K,过点D作DF⊥y轴于点F.
由∠AEB=∠AOB=90°易得∠DBO=∠CAO.
∵∠BOK=∠COD=90°,
∴∠BOC=∠DOK,
∴∠AOB+∠BOC=∠BOK+∠DOK,
∴∠AOC=∠BOD.
在△AOC与△BOD中,∵
∴△AOC≌△BOD,
∴OC=OD.
由∠COD=∠FOK=90°,
易得∠DOF=∠COK.
在△ODF与△OCK中,
∵
∴△ODF≌△OCK,
∴DF=CK=2,OK=OF=3.
又∵点D在第二象限,
∴D(-2,3).
(3)AG=PG+OP.证明:如图图②,延长GP到点L,使LP=OP,连接AL.
在△AON与△BOM中,
∵
∴△AON≌△BOM,
∴∠OAN=∠OBM.
∵OA=OB,∴∠OBA=∠OAB=45°,
∴∠MBA=∠NAB.
∵PG⊥BM,OP⊥AN,
∴∠NAB+∠APO=∠MBA+∠GPB=90°,
∴∠APO=∠GPB=∠APL.
在△LAP与△OAP中,
∵
∴△LAP≌△OAP,
∴∠POA=∠L,∠OAP=∠PAL=45°,
∴∠OAL=90°.
∵∠POA=90°-∠POB,∠GAL=90°-∠OAN,∠POB=∠OAN,
∴∠POA=∠GAL,
∴∠POA=∠GAL=∠L,则AG=GL,
∴AG=GL=PG+PL=PG+OP.
[时间:120分钟 分值:150分]
第Ⅰ卷 (选择题 共40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.全等三角形是 ( )
A.面积和周长相等的两个三角形
B.形状相同的两个三角形
C.能够完全重合的两个三角形
D.三个角对应相等的两个三角形
2.在建筑工地上我们经常看见如图所示用木条EF固定长方形门框ABCD的情形,
这种做法的根据是 ( )
A.两点之间线段最短
B.两点确定一条直线
C.三角形的稳定性
D.长方形的四个角都是直角
3.在平面直角坐标系内,O为坐标原点,A(-4,0),B(0,3).若在该坐标平面内有一个以P(不与点A,B,O重合)为一个顶点的直角三角形与Rt△ABO全等,且这个以P为一个顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的三角形的个数为 ( )
A.9 B.7 C.5 D.3
4.四个角分别相等,四条边分别相等的两个四边形称为全等四边形.已知在四边形ABCD和四边形A'B'C'D'中,AB=A'B',BC=B'C',CD=C'D'.要使四边形ABCD≌四边形A'B'C'D',可以添加的条件是 ( )
A.DA=D'A' B.∠B=∠B'
C.∠B=∠B',∠C=∠C' D.∠B=∠B',∠D=∠D'
5.是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为 ( )
A.45 cm B.48 cm C.51 cm D.54 cm
6.如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判定△ABC≌△DEF的是
( )
A.AB=DE B.∠A=∠D C.AC=DF D.AC∥FD
7.如图,从下列四个条件:①BC=B'C,②AC=A'C,③∠A'CA=∠B'CB,④AB=A'B'中,任取三个作为条件,余下的一个作为结论,则构成真命题的个数是 ( )
A.1 B.2 C.3 D.4
8.如图,在△ABC中,P,Q分别是BC,AC上的点,过点P作PR⊥AB,PS⊥AC,垂足分别为R,S,若∠QAP=∠QPA,PR=PS,有下列结论:①AP平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
9.如图,在△ABC中,∠ACB=90°,AC=CB,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5 cm,DE=1.7 cm,则BE的长为 ( )
A.0.8 cm B.0.7 cm C.0.6 cm D.1 cm
10.如图所示,AD是△ABC的中线,E,F分别是AD及AD延长线上的点,且DE=DF,连接BF,CE,有下列结论:①△BDF≌△CDE;②CE=BF;③△ABD和△ACD的面积相等;④BF∥CE.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷 (非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知:△ABC≌△A'B'C',∠A=∠A',∠B=∠B',∠C=70°,AB=15 cm,则∠C'= °,A'B'=
cm.
12.如图,AB=12 cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4 cm,点P从点B向点A运动,每分钟走1 cm,点Q从点B向点D运动,每分钟走2 cm,P,Q两点同时出发,运动 min后△CAP与△PBQ全等.
13.如图,点A在直线l1:y=-3x上,点B在经过原点O的直线l2上,如图果点A的纵坐标与点B的横坐标相等,且OA=OB,那么直线l2的函数表达式是 .
14.如图,在△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm.点P从点A出发沿AC路径向终点C运动,点Q从点B出发沿BCA路径向终点A运动.点P,Q分别以1 cm/s和2 cm/s的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和点Q作PE⊥l于点E,QF⊥l于点F,则点P运动 s时,△PEC≌△QFC.
三、解答题(本大题共2小题,每小题8分,满分16分)
15.已知:如图,点D,E分别在AB,AC上,且AB=AC,添加一个条件,使△AEB≌△ADC,并写出证明过程.
16.如图,为了测量湖宽AB,先在AB的延长线上选定点C,再选一适当的点M,然后延长BM,CM到点B',C',使MB'=MB,MC'=MC.又在C'B'的延长线上找一点A',使A',M,A三点在同一直线上,这时,只要测出线段A'B'的长度就可以知道湖宽,你能说明其中的道理吗
四、解答题(本大题共2小题,每小题8分,满分16分)
17.如图所示,在△ABC中,点A的坐标为(0,1),点C的坐标为(4,3).如图果要使△ABD与△ABC全等,求点D的坐标.
18.如图所示,在△ABC中,AB=AC,∠1=∠2,AD⊥CD于点D,AE⊥BE于点E,BE,CD交于点O.
求证:(1)△ADC≌△AEB;
(2)OD=OE.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.如图,AD=CB,E,F是AC上的两个动点(不与点A,C重合),且有DE=BF.
(1)若点E,F运动至如图图①所示的位置,且AF=CE.求证:△ADE≌△CBF;
(2)若点E,F运动至如图图②所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗 为什么
(3)在(1)(2)的条件下,AD和CB平行吗 请说明理由.
20.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,点D在线段AB上,AD=AC,AF平分∠CAE交CE于点F.
(1)求证:FD∥CB;
(2)如图图②,若点D在线段BA的延长线上,AF是∠CAD的平分线AM的反向延长线,其他条件不变,(1)中的结论是否仍然成立 并说明理由.
六、解答题(本题12分)
21.如图,已知Rt△ABC≌Rt△DBE,∠ACB=∠DEB=90°.
(1)将两三角形按图①所示方式摆放,其中点E落在AB上,DE所在直线交边AC于点F.求证:AF+EF=DE.
(2)若将两三角形按照图②所示方式摆放,边AC的延长线与DE相交于点F.你认为(1)中的结论还成立吗 若成立,写出证明过程;若不成立,请写出AF,EF与DE之间的数量关系,并说明理由.
七、解答题(本题12分)
22.问题情境:如图①,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,可知∠BAD=∠C(不需要证明).
(1)特例探究:如图图②,∠MAN=90°,射线AE在这个角的内部,点B,C分别在∠MAN的边AM,AN上,且AB=CA,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)归纳证明:如图图③,点B,C分别在∠MAN的边AM,AN上,点E,F在∠MAN内部的射线AD上,∠1,∠2分别是△ABE,△CAF的外角,已知AB=CA,∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)拓展应用:如图图④,在△ABC中,AB=CA,AB>BC.点D在边BC上,CD=2BD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .
八、解答题(本题14分)
23.如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a,b满足|a+b|+(a-5)2=0.
(1)点A的坐标为 ,点B的坐标为 ;
(2)如图图①,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE的延长线于点D,试求点D的坐标;
(3)如图图②,M,N分别为OA,OB边上的点,OM=ON,OP⊥AN,过点P作PG⊥BM交AN的延长线于点G,请写出线段AG,OP与PG之间的数量关系,并证明你的结论.(提示:有两个角相等的三角形是等腰三角形,即“等角对等边”)
答案
第14章综合提升卷
1.C A项,面积和周长相等的两个三角形不一定全等,故此选项错误;
B项,形状相同的两个三角形不一定全等,故此选项错误;
C项,能够完全重合的两个三角形一定全等,故此选项正确;
D项,三个角对应相等的两个三角形不一定全等,故此选项错误.故选C.
2.C
3.A 分别以OA,OB,AB为公共边作与Rt△ABO全等的三角形各有3个,则所有符合条件的三角形个数为9.故选A.
4.C 添加的条件是∠B=∠B',∠C=∠C'.如图图,连接AC,A'C',
在△ABC和△A'B'C'中,∵
∴△ABC≌△A'B'C',(SAS)
∴∠ACB=∠A'C'B',∠BAC=∠B'A'C',AC=A'C'.
∵∠BCD=∠B'C'D',
∴∠ACD=∠A'C'D'.
在△ACD和△A'C'D'中,
∵
∴△ACD≌△A'C'D',(SAS)
∴∠D=∠D',AD=A'D',∠DAC=∠D'A'C',
∴∠BAD=∠B'A'D',
∴四边形ABCD≌四边形A'B'C'D'.
故选C.
5.A ∵BF=EC,BC=BF+CF,EF=EC+CF,∴BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),∴C△DEF=C△ABC=24 cm.
∵CF=3 cm,∴制成整个金属框架所需这种材料的总长度为C△DEF+C△ABC-CF=24+24-3=45(cm).故选A.
6.C
7.B 当①②③为条件,④为结论时:∵∠A'CA=∠B'CB,∴∠ACB=∠A'CB'.又∵BC=B'C,AC=A'C,∴△ACB≌△A'CB',∴AB=A'B';当①②④为条件,③为结论时:∵BC=B'C,AC=A'C,AB=A'B',∴△ACB≌△A'CB',∴∠A'CB'=∠ACB,∴∠A'CA=∠B'CB.故选B.
8.B ①∵PR⊥AB,PS⊥AC,PR=PS,AP=AP,∴Rt△APR≌Rt△APS,∴∠PAR=∠PAS,∴AP平分∠BAC;
②由△APR≌△APS,可得AS=AR;
③∵∠PAR=∠QAP,∠QAP=∠QPA,
∴∠QPA=∠PAR,∴QP∥AR;
④∵PR⊥AB,PS⊥AC,∴∠BRP=∠CSP.
∵PR=PS,BR不一定等于CS,∴△BRP不一定与△CSP全等(只具备一角一边的两三角形不一定全等).故选B.
9.A ∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.
∵∠BCE+∠DCA=90°,∴∠EBC=∠DCA.
在△CEB和△ADC中,∵
∴△CEB≌△ADC,(AAS)
∴BE=CD,CE=AD=2.5 cm.
∵CD=CE-DE,DE=1.7 cm,
∴CD=2.5-1.7=0.8(cm),
∴BE=0.8 cm.故选A.
10.D ①∵AD是△ABC的中线,∴BD=CD.
在△BDF和△CDE中,∵
∴△BDF≌△CDE;
②∵△BDF≌△CDE,∴CE=BF;
③∵AD是△ABC的中线,∴S△ABD=S△ACD;
④∵△BDF≌△CDE,∴∠CED=∠BFD,
∴BF∥CE.故选D.
11.70 15 全等三角形的对应边相等,对应角相等.
12.4 ∵CA⊥AB于点A,DB⊥AB于点B,∴∠A=∠B=90°.设运动x min后△CAP与△PBQ全等,则BP=x cm,BQ=2x cm,则AP=(12-x)cm,分两种情况:①若BP=AC,则x=4,AP=12-4=8(cm),BQ=8 cm,AP=BQ,∴△CAP≌△PBQ;②若BP=AP,则12-x=x,解得x=6,BQ=12≠AC,此时△CAP与△PBQ不全等.
综上所述,运动4 min后△CAP与△PBQ全等.
故答案为4.
13.y=x 如图图,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D.
∵点A的纵坐标与点B的横坐标相等,
∴OC=OD.
在Rt△AOC与Rt△BOD中,∵
∴Rt△AOC≌Rt△BOD,
∴AC=BD.
∵点A在直线l1:y=-3x上,
∴设A(-m,3m),
∴AC=BD=m,OD=OC=3m,
∴B(3m,m).
设直线l2的函数表达式为y=kx,
将B(3m,m)代入,得3mk=m,
∴k=,
∴直线l2的函数表达式为y=x.
14.2或 当△PEC≌△QFC时,则有PC=QC.
分两种情况:
①当点Q在线段BC上时,有8-2t=6-t,解得t=2;②当点Q在线段AC上时,2t-8=6-t,解得t=.故答案为2或.
15.解:本题答案不唯一,如图添加AE=AD.证明如图下:
在△AEB和△ADC中,
∵∴△AEB≌△ADC.(SAS)
16.解:在△MBC与△MB'C'中,
∵
∴△MBC≌△MB'C',(SAS)
∴∠MBC=∠MB'C',
∴∠MBA=∠MB'A'.
在△MBA与△MB'A'中,
∵
∴△MBA≌△MB'A',(ASA)∴AB=A'B'.
即只要测出线段A'B'的长度就可以知道湖宽.
17.解:如图图所示,点D的坐标是(-1,3)或(-1,-1)或(4,-1).
18.证明:(1)∵AD⊥DC,AE⊥BE,
∴∠ADC=∠AEB=90°.
∵∠DAC=∠DAE+∠2,∠EAB=∠DAE+∠1,
且∠1=∠2,∴∠DAC=∠EAB.
在△ADC 与△AEB中,
∵
∴△ADC≌△AEB.(AAS)
(2)如图图,连接AO.
∵△ADC≌△AEB,∴AD=AE.
在Rt△ADO和Rt△AEO中,
∵
∴Rt△ADO≌Rt△AEO,(HL)
∴OD=OE.
19.解:(1)证明:∵AF=CE,
∴AF+EF=CE+EF,即AE=CF.
在△ADE和△CBF中,∵
∴△ADE≌△CBF.(SSS)
(2)△ADE≌△CBF仍成立.
理由:∵AF=CE,
∴AF-EF=CE-EF,即AE=CF.
在△ADE和△CBF中,
∵
∴△ADE≌△CBF.(SSS)
(3)AD∥CB.
理由:∵△ADE≌△CBF,∴∠A=∠C,
∴AD∥CB.
20.解:(1)证明:∵AF平分∠CAE,
∴∠DAF=∠CAF.
在△DAF和△CAF中,
∵
∴△DAF≌△CAF,(SAS)
∴∠ACE=∠ADF.
∵∠ACE+∠ECB=90°,∠B+∠ECB=90°,
∴∠B=∠ACE,
∴∠ADF=∠B,∴FD∥CB.
(2)成立.理由:同(1)可证△DAF≌△CAF,
∴∠D=∠ACF.
∵CE⊥AB,∴∠D+∠DFE=90°.
又∵∠ACF+∠FCB=90°,
∴∠DFE=∠FCB,
∴FD∥CB.
21.解:由Rt△ABC≌Rt△DBE,知BC=BE,AC=DE.
(1)证明:如图图①,连接BF.
在Rt△BCF和Rt△BEF中,
∵∴Rt△BCF≌Rt△BEF,(HL)
∴CF=EF.
∵AC=DE,AF+CF=AC,
∴AF+EF=DE.
(2)(1)中的结论不成立,关系为AF=EF+DE.
理由:如图图②,连接BF.
在Rt△BEF和Rt△BCF中,
∵
∴Rt△BEF≌Rt△BCF,(HL)
∴EF=CF.
∵AC=DE,AF=CF+AC,
∴AF=EF+DE.
22.解:(1)证明:∵CF⊥AE,BD⊥AE,
∴∠BDA=∠AFC=90°,
∴∠ABD+∠BAD=90°.
∵∠MAN=90°,∴∠BAD+∠CAF=90°,
∴∠ABD=∠CAF.
在△ABD和△CAF中,∵
∴△ABD≌△CAF.(AAS)
(2)证明:∵∠1=∠2=∠BAC,∠1=∠BAE+∠ABE,∠BAC=∠BAE+∠CAF,∠2=∠ACF+∠CAF,
∴∠ABE=∠CAF,∠BAE=∠ACF.
在△ABE和△CAF中,∵
∴△ABE≌△CAF.(ASA)
(3)∵△ABC的面积为15,CD=2BD,
∴△ABD的面积是×15=5.
同(3)可证出△ABE≌△CAF,
∴△ACF与△BDE的面积之和等于△ABE与△BDE的面积之和,即等于△ABD的面积.
故答案为5.
23.解:(1)∵|a+b|+(a-5)2=0,∴a=5,b=-5,
∴点A的坐标为(5,0),点B的坐标为(0,-5).
(2)如图图①,过点C作CK⊥x轴于点K,过点D作DF⊥y轴于点F.
由∠AEB=∠AOB=90°易得∠DBO=∠CAO.
∵∠BOK=∠COD=90°,
∴∠BOC=∠DOK,
∴∠AOB+∠BOC=∠BOK+∠DOK,
∴∠AOC=∠BOD.
在△AOC与△BOD中,∵
∴△AOC≌△BOD,
∴OC=OD.
由∠COD=∠FOK=90°,
易得∠DOF=∠COK.
在△ODF与△OCK中,
∵
∴△ODF≌△OCK,
∴DF=CK=2,OK=OF=3.
又∵点D在第二象限,
∴D(-2,3).
(3)AG=PG+OP.证明:如图图②,延长GP到点L,使LP=OP,连接AL.
在△AON与△BOM中,
∵
∴△AON≌△BOM,
∴∠OAN=∠OBM.
∵OA=OB,∴∠OBA=∠OAB=45°,
∴∠MBA=∠NAB.
∵PG⊥BM,OP⊥AN,
∴∠NAB+∠APO=∠MBA+∠GPB=90°,
∴∠APO=∠GPB=∠APL.
在△LAP与△OAP中,
∵
∴△LAP≌△OAP,
∴∠POA=∠L,∠OAP=∠PAL=45°,
∴∠OAL=90°.
∵∠POA=90°-∠POB,∠GAL=90°-∠OAN,∠POB=∠OAN,
∴∠POA=∠GAL,
∴∠POA=∠GAL=∠L,则AG=GL,
∴AG=GL=PG+PL=PG+OP.
