沪科版数学八年级上册同步提优训练:第15章 轴对称图形与等腰三角形 综合提升卷(word,含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步提优训练:第15章 轴对称图形与等腰三角形 综合提升卷(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 462.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 11:10:50 | ||
图片预览




文档简介
第15章综合提升卷
[时间:120分钟 分值:150分]
第Ⅰ卷 (选择题 共40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,其中是轴对称图形的是 ( )
2.如图,△OAB和△OA'B'关于直线OP对称,则下列说法错误的是 ( )
A.OA=OA'
B.线段AA'被直线OP平分
C.∠A=∠A'
D.OP不是BB'的垂直平分线
3.已知点D在△ABC的边AB的垂直平分线上,且AD+DC=AC,若AC=5 cm,BC=4 cm,则△BCD的周长为 ( )
A.6 cm B.7 cm C.8 cm D.9 cm
4.如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在
( )
A.∠A,∠B的平分线的交点处
B.AB的垂直平分线与∠B的平分线的交点处
C.BC的垂直平分线与∠A的平分线的交点处
D.AB,BC的垂直平分线的交点处
5.如图,∠EAF=15°,AB=BC=CD=DE=EF,则∠DEF的度数为 ( )
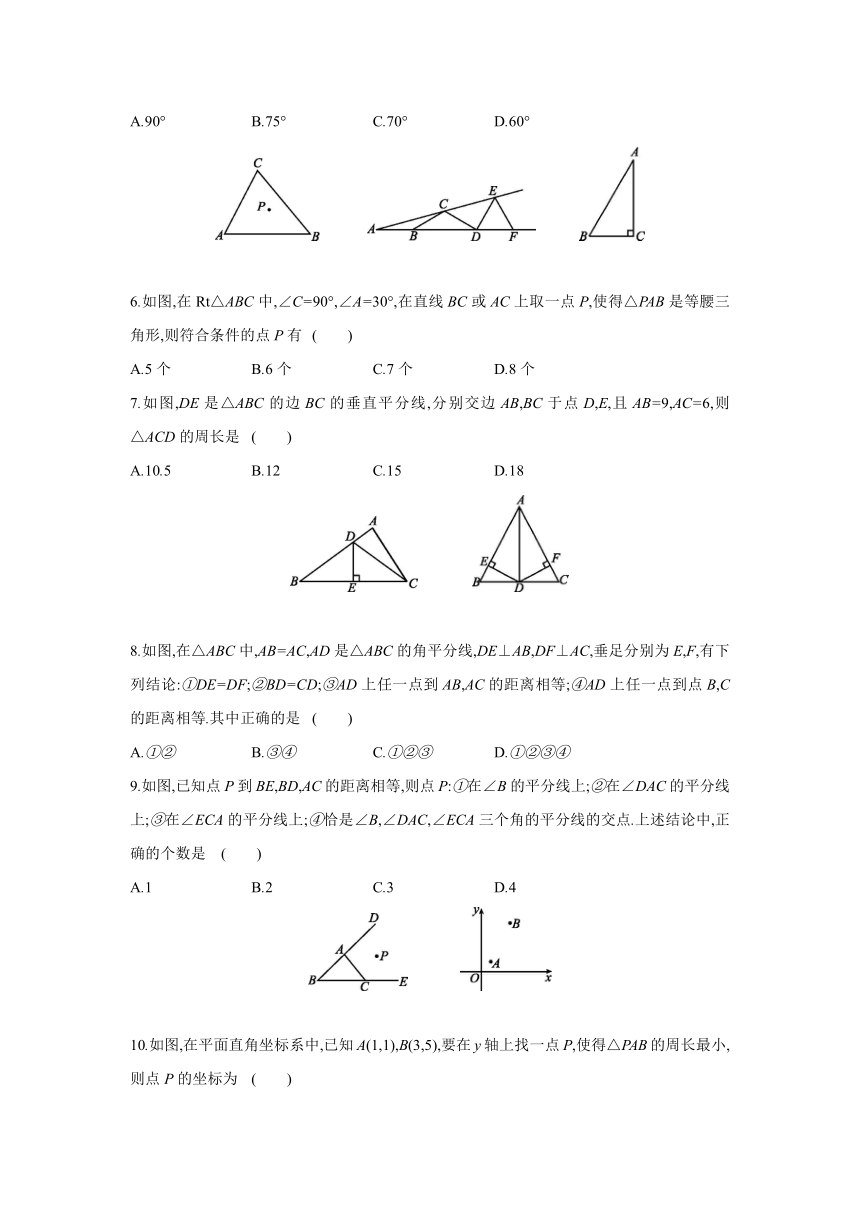
A.90° B.75° C.70° D.60°
6.如图,在Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有 ( )
A.5个 B.6个 C.7个 D.8个
7.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是 ( )
A.10.5 B.12 C.15 D.18
8.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,有下列结论:①DE=DF;②BD=CD;③AD上任一点到AB,AC的距离相等;④AD上任一点到点B,C的距离相等.其中正确的是 ( )
A.①② B.③④ C.①②③ D.①②③④
9.如图,已知点P到BE,BD,AC的距离相等,则点P:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.上述结论中,正确的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,在平面直角坐标系中,已知A(1,1),B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为 ( )
A.(0,1) B.(0,2) C.,0 D.(2,0)
第Ⅱ卷 (非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个等腰三角形的一个角为80°,则它的顶角的度数是 .
12.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60°方向上的500 m处,那么水塔所在的位置到公路的距离AB是 m.
13.如图所示,在边长为2的等边三角形ABC中,E,F,G分别为AB,AC,BC的中点,P是线段EF上的一个动点,连接BP,GP,则△BPG周长的最小值是 .
14.如图,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列三个结论中正确的是 (只填序号).
①点P在∠BAC的平分线上;②PQ∥AR;③△BRP≌△QSP.
三、解答题(本大题共2小题,每小题8分,满分16分)
15.如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置 请在图上标出它的位置.(尺规作图,保留痕迹)
16.如图,已知∠DAC是△ABC的一个外角,请在下列三个条件:①∠B=∠C;②AE平分∠DAC;③AE∥BC中任选出两个条件作为已知条件,另一个条件作为结论,组成一个命题.
(1)请写出所有的真命题(写成“ ”的形式);
(2)请选择其中的一个真命题加以证明.
四、解答题(本大题共2小题,每小题8分,满分16分)
17.如图,在8×8的网格中,每个小正方形的边长都为1.
(1)请在网格中建立平面直角坐标系,使点A,C的坐标分别为(-4,3),(-1,2);
(2)画出△ABC关于y轴的对称图形△A1B1C1,并写出点B1的坐标;
(3)求出△A1B1C1的面积.
18.如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE∶∠EAB=4∶1.
(1)求证:AE=BE;
(2)求证:∠AEC=2∠B;
(3)求∠B的度数.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.如图①,在△ABC中,AB=AC,∠A=36°,我们发现这个三角形有一种特性,即经过它某一顶点的一条射线可把它分成两个小等腰三角形.据此,请你解答问题.
如图图②,在△ABC中,AB=AC,∠A=108°,请你在图中画一条射线(不必写画法),把它分成两个小等腰三角形,并写出底角的大小.
20.如图,在△ABC中,BA=BC,点D在边BC上,且DB=DA=AC.
(1)如图图(a),填空:∠B= °,∠C= °.
(2)若M为线段BC上的点,过点M作直线MH⊥AD交AD的延长线于点H,与直线AB,AC分别交于点N,E,如图图(b).
①求证:△ANE是等腰三角形;
②试写出线段BN,CE,CD之间的数量关系,并加以证明.
六、解答题(本题12分)
21.如图,在△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(点D不与点A,B重合),连接CD,作∠CDE=30°,DE交AC于点E.
(1)当DE∥BC时,△ACD的形状按角分类是 三角形.
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗 若可以,请求出∠AED的度数;若不可以,请说明理由.
七、解答题(本题12分)
22.(1)如图①,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,则有DE=DF,AE=AF,请加以证明;
(2)如图图②,在(1)的情况下,如图果∠MDN=∠EDF,∠MDN的两边分别与AB,AC相交于点M,N,其他条件不变,那么AM+ =2AF,请加以证明;
(3)如图图③,在Rt△ABC中,∠C=90°,∠BAC=60°,AC=6,AD平分∠BAC交BC于点D,∠MDN=120°,ND∥AB,求四边形AMDN的周长.
八、解答题(本题14分)
23.(1)如图①,在△ABC中,AB>AC>BC,∠ACB=80°,点D,E分别在线段BA,AB的延长线上,且AD=AC,BE=BC,则∠DCE的度数为 ;
(2)如图图②,在△ABC中,AB>AC>BC,∠ACB=80°,点D,E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D,E分别在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案).
答案
第15章综合提升卷
1.D 根据轴对称的定义可知应选D.
2.D ∵△OAB和△OA'B'关于直线OP对称,∴OA=OA',故A选项正确,不符合题意;线段AA'被直线OP平分,故B选项正确,不符合题意;∠A=∠A',故C选项正确,不符合题意;OP是BB'的垂直平分线,故D选项不正确,符合题意.故选D.
3.D ∵AD+DC=AC,∴点D在AC边上,如图图.
∵点D在△ABC的边AB的垂直平分线上,∴BD=AD.
∵AD+DC=AC=5 cm,BC=4 cm,∴△BCD的周长为BD+DC+BC=AD+DC+BC=AC+BC=9 cm.故选D.
4.D 根据线段垂直平分线的性质:线段垂直平分线上的点到线段两个端点的距离相等,即可得出符合条件的点在AB,BC的垂直平分线的交点处.故选D.
5.D ∵AB=BC,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
则∠BCD=180°-(∠CBD+∠BDC)=180°-60°=120°,
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°,
∴∠CDE=180°-(∠ECD+∠CED)=180°-90°=90°,
则∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°,
∴∠DEF=180°-(∠EDF+∠EFD)=180°-120°=60°.
故选D.
6.B 如图图,第1个点在线段CA的延长线上,取一点P,使BA=AP;第2个点在线段CB的延长线上,取一点P,使AB=PB;第3个点在线段AC的延长线上,取一点P,使AB=PB;第4个点在线段BC的延长线上,取一点P,使AB=PA;第5个点在线段AC的延长线上,取一点P,使AB=AP;第6个点在线段AC上,取一点P,使AP=PB,∴符合条件的点P有6个.故选B.
7.C ∵DE是△ABC的边BC的垂直平分线,
∴DB=DC,
∴△ACD的周长=AD+CD+AC=AD+BD+AC=AB+AC.
∵AB=9,AC=6,
∴△ACD的周长=9+6=15.
故选C.
8.D ∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,且AD上任一点到AB,AC的距离相等.
又∵AB=AC,根据“三线合一”的性质,可得AD垂直平分BC,∴BD=CD,AD上任一点到点B,C的距离相等.故选D.
9.D
10.B 如图图,作点A关于y轴的对称点A',连接A'B交y轴于点P.
∵A(1,1),∴A'(-1,1).
设直线A'B的函数表达式为y=kx+b(k≠0),
∴
解得
∴直线A'B的函数表达式为y=x+2,
∴当x=0时,y=2,∴P(0,2).
故选B.
11.80°或20° (1)当80°角为顶角时,顶角度数即为80°;(2)当80°角为底角时,顶角=180°-2×80°=20°.故答案为80°或20°.
12.250 由题意得∠AOB=90°-60°=30°.
∵∠ABO=90°,OA=500 m,∴AB=OA=250 m.
13.3 要使△BPG的周长最小,而BG=1一定,只要使BP+PG的值最小即可.连接AG交EF于点M.∵△ABC是等边三角形,E,F,G分别为AB,AC,BC的中点,∴AG⊥BC,EF∥BC,∴AG⊥EF,AM=MG,∴点A,G关于EF对称,则当点P和点E重合时,BP+PG最小,即△PBG的周长最小,为PB+PG+BG=AE+BE+BG=AB+BG=2+1=3.
14.①②③ ∵PR⊥AB,PS⊥AC,PR=PS,∴点P在∠BAC的平分线上,故①正确;
∵AQ=PQ,∴∠QAP=∠QPA.
∵P在∠BAC的平分线上,
∴∠PAR=∠QAP,
∴∠QPA=∠PAR,
∴PQ∥AR,故②正确;
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∵QP∥AR,∴∠PQS=60°,∴∠B=∠PQS.
在△BRP和△QSP中,
∵
∴△BRP≌△QSP,(AAS)
故③正确.故答案为①②③.
15.解:如图图所示,作∠NOM的平分线和线段AB的垂直平分线,它们的交点为C,则点C就是“英语角”的位置.
16.解:(1)①② ③,①③ ②,②③ ①.
(2)答案不唯一,如图选②③ ①,证明如图下:
∵AE∥BC,∴∠DAE=∠B,∠EAC=∠C.
∵AE平分∠DAC,∴∠DAE=∠EAC,
∴∠B=∠C.
17.解:(1)如图图所示.
(2)如图图所示.点B1的坐标为(2,0).
(3)△A1B1C1的面积为3×3-×1×3-×2×1-×2×3=9-1.5-1-3=3.5.
18.解:(1)证明:∵DE是线段AB的垂直平分线,
∴AE=BE.
(2)证明:∵AE=BE,∴∠B=∠EAD,
∴∠AEC=∠B+∠EAD=2∠B.
(3)设∠B=x°,则∠EAD=x°,∠CAE=4x°,
∴4x+x+x+90=180,解得x=15,即∠B=15°.
19.解:如图图所示,由AB=AC,∠BAC=108°,知∠C=36°.
过点A在∠BAC内部作射线AD,使得∠DAC=36°,则△ACD和△ABD均为等腰三角形.
在△ABD中,∠BAD=∠ADB=72°,
在△ACD中,∠DAC=∠C=36°.
20.解:(1)∵BA=BC,
∴∠C=∠BAC.
∵DA=DB,∴∠BAD=∠B.
∵AD=AC,∴∠ADC=∠C=∠BAC=2∠B,
∴∠DAC=∠B.
∵∠DAC+∠ADC+∠C=180°,
∴∠B+2∠B+2∠B=180°,
∴∠B=36°,∠C=2∠B=72°.
(2)①证明:在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°.
在△ACD中,∵DA=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,∴∠BAD=∠CAD=36°.
∵MH⊥AD,∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,∴AN=AE,
即△ANE是等腰三角形.
②CD=BN+CE.
证明:由①知AN=AE.
又∵BA=BC,DB=AC,
∴BN=BA-AN=BC-AE,
CE=AE-AC=AE-DB,
∴BN+CE=BC-DB=CD,
即CD=BN+CE.
21.解:(1)∵DE∥BC,
∴∠BCD=∠EDC=30°.
∴∠ACD=∠ACB-∠BCD=90°,
∴△ACD是直角三角形.
(2)△ECD可以是等腰三角形.
①当∠CDE=∠ECD时,EC=DE,
∴∠ECD=∠CDE=30°,
∴∠AED=∠ECD+∠CDE=60°;
②当∠ECD=∠CED时,CD=DE.
∵∠ECD+∠CED+∠CDE=180°,
∴∠CED===75°,
∴∠AED=180°-∠CED=105°;
③当∠CED=∠CDE时,EC=CD,
∴∠ACD=180°-∠CED-∠CDE=180°-30°-30°=120°.
∵∠ACB=120°,
∴此时点D与点B重合,不合题意.
综上,△ECD可以是等腰三角形,此时∠AED的度数为60°或105°.
22.解:(1)证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,△ADE与△ADF均为直角三角形.
在Rt△ADE与Rt△ADF中,
∵
∴Rt△ADE≌Rt△ADF,
∴AE=AF.
(2)AN
证明:由(1)得DE=DF.
∵∠MDN=∠EDF,∴∠MDE=∠NDF.
在△MDE和△NDF中,
∵
∴△MDE≌△NDF,(ASA)
∴ME=NF,
∴AM+AN=(AE+ME)+(AF-NF)=AE+AF=2AF.
(3)如图图,过点D作DE⊥AB于点E,易知∠MDN=∠EDC=120°,由(2)可知AM+AN=2AC=2×6=12,△MDE≌△NDC,∴DM=DN.
∵∠BAC=60°,AD平分∠BAC交BC于点D,
∴∠BAD=∠CAD=30°.
∵ND∥AB,
∴∠ADN=∠BAD=30°,∠CDN=∠B=30°,
∴∠CAD=∠ADN,∴AN=DN.
在Rt△CDN中,∠CDN=30°,
∴DN=2CN.
∵AC=6,
∴DN=AN=×6=4,
∴DM=4,
∴四边形AMDN的周长=12+4×2=20.
23. (1)∵AD=AC,BE=BC,
∴∠ACD=∠D,∠BCE=∠E.
∵∠ACB=80°,∴∠CAB+∠CBA=100°,
∴∠CDA+∠BEC=(∠CAB+∠CBA)=50°,
∴∠DCE=130°.
解:(1)130°
(2)∵∠ACB=80°,
∴∠A+∠B=100°.
∵AD=AC,BE=BC,
∴∠ACD=∠ADC,∠BEC=∠BCE,
∴∠ADC=,∠BEC=,
∴∠ADC+∠BEC=180°-(∠A+∠B)=130°,
∴∠DCE=50°.
(3)点D,E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图图(a).
∵∠ACB=80°,
∴∠CAB+∠B=100°.
∵AD=AC,BE=BC,
∴∠ADC=∠ACD,∠BEC=∠BCE.
∵∠CAB=∠ADC+∠ACD,∠B+∠BEC+∠BCE=180°,
∴∠ADC=∠CAB,∠BEC=.
∵∠BEC=∠ADC+∠DCE,
∴=∠CAB+∠DCE,
∴∠DCE=40°.
如图图(b),同理∠DCE=40°.
综上所述,∠DCE的度数为130°或50°或40°.
[时间:120分钟 分值:150分]
第Ⅰ卷 (选择题 共40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下面四个图形分别是节能、节水、低碳和绿色食品标志,其中是轴对称图形的是 ( )
2.如图,△OAB和△OA'B'关于直线OP对称,则下列说法错误的是 ( )
A.OA=OA'
B.线段AA'被直线OP平分
C.∠A=∠A'
D.OP不是BB'的垂直平分线
3.已知点D在△ABC的边AB的垂直平分线上,且AD+DC=AC,若AC=5 cm,BC=4 cm,则△BCD的周长为 ( )
A.6 cm B.7 cm C.8 cm D.9 cm
4.如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在
( )
A.∠A,∠B的平分线的交点处
B.AB的垂直平分线与∠B的平分线的交点处
C.BC的垂直平分线与∠A的平分线的交点处
D.AB,BC的垂直平分线的交点处
5.如图,∠EAF=15°,AB=BC=CD=DE=EF,则∠DEF的度数为 ( )
A.90° B.75° C.70° D.60°
6.如图,在Rt△ABC中,∠C=90°,∠A=30°,在直线BC或AC上取一点P,使得△PAB是等腰三角形,则符合条件的点P有 ( )
A.5个 B.6个 C.7个 D.8个
7.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是 ( )
A.10.5 B.12 C.15 D.18
8.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,有下列结论:①DE=DF;②BD=CD;③AD上任一点到AB,AC的距离相等;④AD上任一点到点B,C的距离相等.其中正确的是 ( )
A.①② B.③④ C.①②③ D.①②③④
9.如图,已知点P到BE,BD,AC的距离相等,则点P:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.上述结论中,正确的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,在平面直角坐标系中,已知A(1,1),B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为 ( )
A.(0,1) B.(0,2) C.,0 D.(2,0)
第Ⅱ卷 (非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个等腰三角形的一个角为80°,则它的顶角的度数是 .
12.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60°方向上的500 m处,那么水塔所在的位置到公路的距离AB是 m.
13.如图所示,在边长为2的等边三角形ABC中,E,F,G分别为AB,AC,BC的中点,P是线段EF上的一个动点,连接BP,GP,则△BPG周长的最小值是 .
14.如图,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列三个结论中正确的是 (只填序号).
①点P在∠BAC的平分线上;②PQ∥AR;③△BRP≌△QSP.
三、解答题(本大题共2小题,每小题8分,满分16分)
15.如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置 请在图上标出它的位置.(尺规作图,保留痕迹)
16.如图,已知∠DAC是△ABC的一个外角,请在下列三个条件:①∠B=∠C;②AE平分∠DAC;③AE∥BC中任选出两个条件作为已知条件,另一个条件作为结论,组成一个命题.
(1)请写出所有的真命题(写成“ ”的形式);
(2)请选择其中的一个真命题加以证明.
四、解答题(本大题共2小题,每小题8分,满分16分)
17.如图,在8×8的网格中,每个小正方形的边长都为1.
(1)请在网格中建立平面直角坐标系,使点A,C的坐标分别为(-4,3),(-1,2);
(2)画出△ABC关于y轴的对称图形△A1B1C1,并写出点B1的坐标;
(3)求出△A1B1C1的面积.
18.如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE∶∠EAB=4∶1.
(1)求证:AE=BE;
(2)求证:∠AEC=2∠B;
(3)求∠B的度数.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.如图①,在△ABC中,AB=AC,∠A=36°,我们发现这个三角形有一种特性,即经过它某一顶点的一条射线可把它分成两个小等腰三角形.据此,请你解答问题.
如图图②,在△ABC中,AB=AC,∠A=108°,请你在图中画一条射线(不必写画法),把它分成两个小等腰三角形,并写出底角的大小.
20.如图,在△ABC中,BA=BC,点D在边BC上,且DB=DA=AC.
(1)如图图(a),填空:∠B= °,∠C= °.
(2)若M为线段BC上的点,过点M作直线MH⊥AD交AD的延长线于点H,与直线AB,AC分别交于点N,E,如图图(b).
①求证:△ANE是等腰三角形;
②试写出线段BN,CE,CD之间的数量关系,并加以证明.
六、解答题(本题12分)
21.如图,在△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(点D不与点A,B重合),连接CD,作∠CDE=30°,DE交AC于点E.
(1)当DE∥BC时,△ACD的形状按角分类是 三角形.
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗 若可以,请求出∠AED的度数;若不可以,请说明理由.
七、解答题(本题12分)
22.(1)如图①,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,则有DE=DF,AE=AF,请加以证明;
(2)如图图②,在(1)的情况下,如图果∠MDN=∠EDF,∠MDN的两边分别与AB,AC相交于点M,N,其他条件不变,那么AM+ =2AF,请加以证明;
(3)如图图③,在Rt△ABC中,∠C=90°,∠BAC=60°,AC=6,AD平分∠BAC交BC于点D,∠MDN=120°,ND∥AB,求四边形AMDN的周长.
八、解答题(本题14分)
23.(1)如图①,在△ABC中,AB>AC>BC,∠ACB=80°,点D,E分别在线段BA,AB的延长线上,且AD=AC,BE=BC,则∠DCE的度数为 ;
(2)如图图②,在△ABC中,AB>AC>BC,∠ACB=80°,点D,E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D,E分别在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案).
答案
第15章综合提升卷
1.D 根据轴对称的定义可知应选D.
2.D ∵△OAB和△OA'B'关于直线OP对称,∴OA=OA',故A选项正确,不符合题意;线段AA'被直线OP平分,故B选项正确,不符合题意;∠A=∠A',故C选项正确,不符合题意;OP是BB'的垂直平分线,故D选项不正确,符合题意.故选D.
3.D ∵AD+DC=AC,∴点D在AC边上,如图图.
∵点D在△ABC的边AB的垂直平分线上,∴BD=AD.
∵AD+DC=AC=5 cm,BC=4 cm,∴△BCD的周长为BD+DC+BC=AD+DC+BC=AC+BC=9 cm.故选D.
4.D 根据线段垂直平分线的性质:线段垂直平分线上的点到线段两个端点的距离相等,即可得出符合条件的点在AB,BC的垂直平分线的交点处.故选D.
5.D ∵AB=BC,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
则∠BCD=180°-(∠CBD+∠BDC)=180°-60°=120°,
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°,
∴∠CDE=180°-(∠ECD+∠CED)=180°-90°=90°,
则∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°,
∴∠DEF=180°-(∠EDF+∠EFD)=180°-120°=60°.
故选D.
6.B 如图图,第1个点在线段CA的延长线上,取一点P,使BA=AP;第2个点在线段CB的延长线上,取一点P,使AB=PB;第3个点在线段AC的延长线上,取一点P,使AB=PB;第4个点在线段BC的延长线上,取一点P,使AB=PA;第5个点在线段AC的延长线上,取一点P,使AB=AP;第6个点在线段AC上,取一点P,使AP=PB,∴符合条件的点P有6个.故选B.
7.C ∵DE是△ABC的边BC的垂直平分线,
∴DB=DC,
∴△ACD的周长=AD+CD+AC=AD+BD+AC=AB+AC.
∵AB=9,AC=6,
∴△ACD的周长=9+6=15.
故选C.
8.D ∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,且AD上任一点到AB,AC的距离相等.
又∵AB=AC,根据“三线合一”的性质,可得AD垂直平分BC,∴BD=CD,AD上任一点到点B,C的距离相等.故选D.
9.D
10.B 如图图,作点A关于y轴的对称点A',连接A'B交y轴于点P.
∵A(1,1),∴A'(-1,1).
设直线A'B的函数表达式为y=kx+b(k≠0),
∴
解得
∴直线A'B的函数表达式为y=x+2,
∴当x=0时,y=2,∴P(0,2).
故选B.
11.80°或20° (1)当80°角为顶角时,顶角度数即为80°;(2)当80°角为底角时,顶角=180°-2×80°=20°.故答案为80°或20°.
12.250 由题意得∠AOB=90°-60°=30°.
∵∠ABO=90°,OA=500 m,∴AB=OA=250 m.
13.3 要使△BPG的周长最小,而BG=1一定,只要使BP+PG的值最小即可.连接AG交EF于点M.∵△ABC是等边三角形,E,F,G分别为AB,AC,BC的中点,∴AG⊥BC,EF∥BC,∴AG⊥EF,AM=MG,∴点A,G关于EF对称,则当点P和点E重合时,BP+PG最小,即△PBG的周长最小,为PB+PG+BG=AE+BE+BG=AB+BG=2+1=3.
14.①②③ ∵PR⊥AB,PS⊥AC,PR=PS,∴点P在∠BAC的平分线上,故①正确;
∵AQ=PQ,∴∠QAP=∠QPA.
∵P在∠BAC的平分线上,
∴∠PAR=∠QAP,
∴∠QPA=∠PAR,
∴PQ∥AR,故②正确;
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∵QP∥AR,∴∠PQS=60°,∴∠B=∠PQS.
在△BRP和△QSP中,
∵
∴△BRP≌△QSP,(AAS)
故③正确.故答案为①②③.
15.解:如图图所示,作∠NOM的平分线和线段AB的垂直平分线,它们的交点为C,则点C就是“英语角”的位置.
16.解:(1)①② ③,①③ ②,②③ ①.
(2)答案不唯一,如图选②③ ①,证明如图下:
∵AE∥BC,∴∠DAE=∠B,∠EAC=∠C.
∵AE平分∠DAC,∴∠DAE=∠EAC,
∴∠B=∠C.
17.解:(1)如图图所示.
(2)如图图所示.点B1的坐标为(2,0).
(3)△A1B1C1的面积为3×3-×1×3-×2×1-×2×3=9-1.5-1-3=3.5.
18.解:(1)证明:∵DE是线段AB的垂直平分线,
∴AE=BE.
(2)证明:∵AE=BE,∴∠B=∠EAD,
∴∠AEC=∠B+∠EAD=2∠B.
(3)设∠B=x°,则∠EAD=x°,∠CAE=4x°,
∴4x+x+x+90=180,解得x=15,即∠B=15°.
19.解:如图图所示,由AB=AC,∠BAC=108°,知∠C=36°.
过点A在∠BAC内部作射线AD,使得∠DAC=36°,则△ACD和△ABD均为等腰三角形.
在△ABD中,∠BAD=∠ADB=72°,
在△ACD中,∠DAC=∠C=36°.
20.解:(1)∵BA=BC,
∴∠C=∠BAC.
∵DA=DB,∴∠BAD=∠B.
∵AD=AC,∴∠ADC=∠C=∠BAC=2∠B,
∴∠DAC=∠B.
∵∠DAC+∠ADC+∠C=180°,
∴∠B+2∠B+2∠B=180°,
∴∠B=36°,∠C=2∠B=72°.
(2)①证明:在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°.
在△ACD中,∵DA=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,∴∠BAD=∠CAD=36°.
∵MH⊥AD,∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,∴AN=AE,
即△ANE是等腰三角形.
②CD=BN+CE.
证明:由①知AN=AE.
又∵BA=BC,DB=AC,
∴BN=BA-AN=BC-AE,
CE=AE-AC=AE-DB,
∴BN+CE=BC-DB=CD,
即CD=BN+CE.
21.解:(1)∵DE∥BC,
∴∠BCD=∠EDC=30°.
∴∠ACD=∠ACB-∠BCD=90°,
∴△ACD是直角三角形.
(2)△ECD可以是等腰三角形.
①当∠CDE=∠ECD时,EC=DE,
∴∠ECD=∠CDE=30°,
∴∠AED=∠ECD+∠CDE=60°;
②当∠ECD=∠CED时,CD=DE.
∵∠ECD+∠CED+∠CDE=180°,
∴∠CED===75°,
∴∠AED=180°-∠CED=105°;
③当∠CED=∠CDE时,EC=CD,
∴∠ACD=180°-∠CED-∠CDE=180°-30°-30°=120°.
∵∠ACB=120°,
∴此时点D与点B重合,不合题意.
综上,△ECD可以是等腰三角形,此时∠AED的度数为60°或105°.
22.解:(1)证明:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,△ADE与△ADF均为直角三角形.
在Rt△ADE与Rt△ADF中,
∵
∴Rt△ADE≌Rt△ADF,
∴AE=AF.
(2)AN
证明:由(1)得DE=DF.
∵∠MDN=∠EDF,∴∠MDE=∠NDF.
在△MDE和△NDF中,
∵
∴△MDE≌△NDF,(ASA)
∴ME=NF,
∴AM+AN=(AE+ME)+(AF-NF)=AE+AF=2AF.
(3)如图图,过点D作DE⊥AB于点E,易知∠MDN=∠EDC=120°,由(2)可知AM+AN=2AC=2×6=12,△MDE≌△NDC,∴DM=DN.
∵∠BAC=60°,AD平分∠BAC交BC于点D,
∴∠BAD=∠CAD=30°.
∵ND∥AB,
∴∠ADN=∠BAD=30°,∠CDN=∠B=30°,
∴∠CAD=∠ADN,∴AN=DN.
在Rt△CDN中,∠CDN=30°,
∴DN=2CN.
∵AC=6,
∴DN=AN=×6=4,
∴DM=4,
∴四边形AMDN的周长=12+4×2=20.
23. (1)∵AD=AC,BE=BC,
∴∠ACD=∠D,∠BCE=∠E.
∵∠ACB=80°,∴∠CAB+∠CBA=100°,
∴∠CDA+∠BEC=(∠CAB+∠CBA)=50°,
∴∠DCE=130°.
解:(1)130°
(2)∵∠ACB=80°,
∴∠A+∠B=100°.
∵AD=AC,BE=BC,
∴∠ACD=∠ADC,∠BEC=∠BCE,
∴∠ADC=,∠BEC=,
∴∠ADC+∠BEC=180°-(∠A+∠B)=130°,
∴∠DCE=50°.
(3)点D,E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图图(a).
∵∠ACB=80°,
∴∠CAB+∠B=100°.
∵AD=AC,BE=BC,
∴∠ADC=∠ACD,∠BEC=∠BCE.
∵∠CAB=∠ADC+∠ACD,∠B+∠BEC+∠BCE=180°,
∴∠ADC=∠CAB,∠BEC=.
∵∠BEC=∠ADC+∠DCE,
∴=∠CAB+∠DCE,
∴∠DCE=40°.
如图图(b),同理∠DCE=40°.
综上所述,∠DCE的度数为130°或50°或40°.
