沪科版数学八年级上册同步提优训练:期末综合提升卷(word、含答案)
文档属性
| 名称 | 沪科版数学八年级上册同步提优训练:期末综合提升卷(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 513.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 12:37:52 | ||
图片预览




文档简介
期末综合提升卷
[时间:120分钟 分值:150分]
第Ⅰ卷 (选择题 共40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知点P的坐标为(-2,a2+1),则点P一定在 ( )
A.第一象限或第三象限 B.第二象限或第四象限
C.第二象限 D.第三象限
2.若将点P(1,-m)向右平移2个单位,再向上平移1个单位得到点Q(n,3),则点(m,n)的坐标为
( )
A.(3,-2) B.(2,-3) C.(3,2) D.(-2,3)
3.下列图形中,不是轴对称图形的是 ( )
A.①⑤ B.②⑤ C.④⑤ D.①②
4.已知不等边三角形的两边长分别是2 cm和9 cm,如图果第三边的长为整数,那么第三边的长为 ( )
A.8 cm B.10 cm C.8 cm或10 cm D.8 cm或9 cm
5.关于一次函数y=-2x+1,下列结论中不正确的是 ( )
A.图象经过点(1,-1) B.图象与两坐标轴围成的三角形的面积为
C.y随x的增大而减小 D.当x<时,y>0
6.在下列一组图形中,全等的三角形是 ( )
A.①和⑥ B.②和④,③和⑤
C.③和⑤ D.②和④
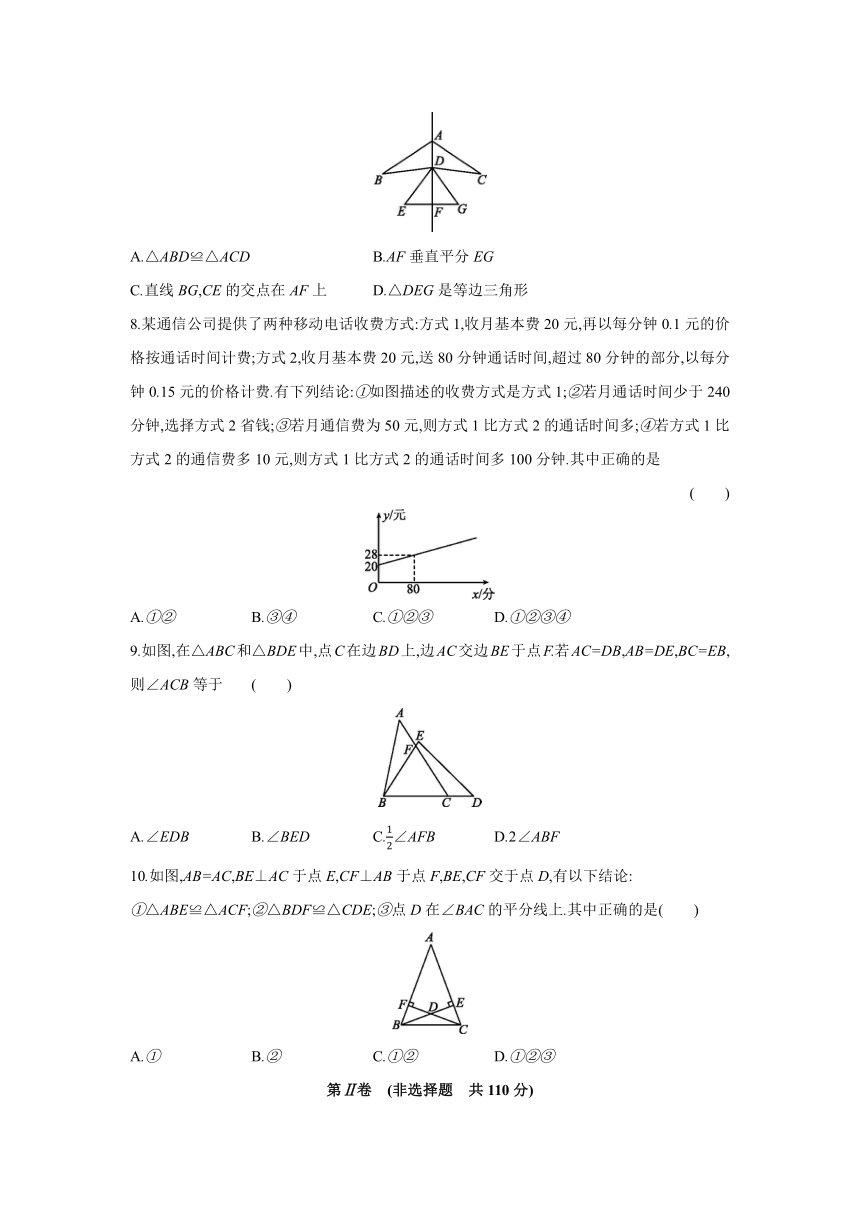
7.是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是 ( )
A.△ABD≌△ACD B.AF垂直平分EG
C.直线BG,CE的交点在AF上 D.△DEG是等边三角形
8.某通信公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.有下列结论:①如图描述的收费方式是方式1;②若月通话时间少于240分钟,选择方式2省钱;③若月通信费为50元,则方式1比方式2的通话时间多;④若方式1比方式2的通信费多10元,则方式1比方式2的通话时间多100分钟.其中正确的是
( )
A.①② B.③④ C.①②③ D.①②③④
9.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=DB,AB=DE,BC=EB,则∠ACB等于 ( )
A.∠EDB B.∠BED C.∠AFB D.2∠ABF
10.如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,有以下结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.其中正确的是( )
A.① B.② C.①② D.①②③
第Ⅱ卷 (非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一副三角尺按放置,若∠1=90°,则∠2的度数为 .
12.在平面直角坐标系中,已知点A(2,3),B(4,7),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为 .
13.如图,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C'恰好落在直线AB上,则点C'的坐标为 .
14.△ABC的高AD,BE所在的直线交于点M,若BM=AC,则∠ABC的度数为 .
三、解答题(本大题共2小题,每小题8分,满分16分)
15.如图,在△ABC中,∠BAC是钝角,按要求完成下列画图(不写作法,保留作图痕迹):
①用尺规作∠BAC的平分线AE;
②用三角尺作AC边上的高BD;
③用尺规作AB边上的垂直平分线MN.
16.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-2,1),C(-2,4).
(1)画出△ABC沿着y轴向下平移5个单位得到的△A1B1C1,并直接写出点C的对应点C1的坐标;
(2)画出△ABC关于y轴对称的△A2B2C2,并直接写出点C的对应点C2的坐标.
四、解答题(本大题共2小题,每小题8分,满分16分)
17.如图,已知∠MBA+∠BAC+∠NCA=360°.
(1)求证:MD∥NE;
(2)若∠ABD=70°,∠ACE=36°,BP和CP分别平分∠ABD,∠ACE,求∠BPC的度数.
18.如图,已知CD是AB的垂直平分线,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)若线段CE的长为3 cm,BC的长为4 cm,求BF的长.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.小明平时喜欢玩游戏,本学期学校组织的几次数学反馈性测试,小明的数学成绩如图下表:
月份x(月) 7 8 9 10
成绩y(分) 90 80 70 60
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在如图所示的平面直角坐标系中描点并连线;
(2)观察(1)中所描点的位置关系,照这样的发展趋势,猜想y与x之间的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉迷于游戏中,照这样的发展趋势,请你估计12月份的测试中小明的数学成绩,并用一句话对小明提出一些建议.
20.如图所示,已知△ABC,分别以AB,AC为腰,以A为顶角的顶点作等腰三角形ABM、等腰三角形ACN,且∠ANC=∠ABM=x,MC与NB的延长线交于点O.
(1)如图图①,若x=45°,则∠O的度数为 ;
(2)如图图②,若x=30°,则∠O的度数为 ;
(3)如图图③,猜想∠BOC的度数(用含x的式子表示),并证明你的结论.
六、解答题(本题12分)
21.在一条笔直的道路上依次有A,B,C三地,男男从A地跑步到C地,同时乐乐从B地跑步到A地,休息1分钟后接到通知,要求乐乐比男男早1分钟到达C地,乐乐立即以比原来快的速度前往C地,两人均匀速运动,如图是男男跑步时间t(分)与两人距A地的距离s(米)之间的函数图象.
(1)a= ,乐乐去A地的速度为 ;
(2)结合图象,求出乐乐从A地到C地时s关于t的函数表达式(写出自变量的取值范围);
(3)请直接写出两人距B地的距离相等的时间.
七、解答题(本题12分)
22.如图,在△ABC中,AB=AC,∠BAC=90°,P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ,PQ,PQ与AC交于点H.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形 若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上的什么位置时,△ACQ是等腰三角形 请说明理由.
八、解答题(本题14分)
23.平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
(1)如图①,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个
(2)过点A,B向直线l:y=-2x作垂线,垂足分别为M,N(如图图②),试判断线段AM,BN,MN之间的数量关系,并说明理由;
(3)过点A,B向动直线l:y=kx(k>0)作垂线,垂足分别为M,N,请直接写出线段AM,BN,MN之间的数量关系.
答案
期末综合提升卷
1.C
2.D 由题意可得n=1+2=3,3=-m+1,则m=-2.故点(m,n)的坐标为(-2,3).故选D.
3.A 根据轴对称的定义判断,①⑤不是轴对称图形.
4.C 根据三角形的三边关系,得7 cm<第三边长<11 cm,故第三边长为8 cm或9 cm或10 cm.
又∵三角形为不等边三角形,∴第三边长不能为9 cm.故选C.
5.B A项,当x=1时,y=-1,∴图象过点(1,-1),故正确,不符合题意;
B项,∵图象与坐标轴交于点,0和(0,1),
∴图象与两坐标轴围成的三角形的面积为,故不正确,符合题意;
C项,∵-2<0,∴y随x的增大而减小,故正确,不符合题意;
D项,∵当x<时,图象在x轴上方,∴y>0,故正确,不符合题意.故选B.
6.D ①⑥只有两个对应角相等,没有对应边相等,不符合条件;②④由两个对应角与这两个角的夹边相等,符合判定两个三角形全等的基本事实ASA;③⑤只有两个对应角相等,没有对应边相等,不符合条件.故选D.
7.D 由轴对称的性质,易知DE=DG,只有当∠EDG=60°或EG=DG时,△DEG才是等边三角形,故D项不一定成立.
8.C 根据题意,得方式1的函数表达式为y1=0.1x+20,方式2的函数表达式为y2=
①当x=80时,方式1的收费是28元,故①正确.
②0.1x+20>0.15x+8,解得x<240,故②正确.
③当y=50时,0.1x+20=50,解得x=300,0.15x+8=50,解得x=280,故③正确.
④当x≤80时,y2=20,令y1=0.1x+20=20+10,解得x=100,不符合方式1比方式2的通话时间多100分钟.
当x>80时,根据题意可得方程组解得符合题意.因此,当方式1比方式2的通信费多10元时,方式1不一定比方式2的通话时间多100分钟,故④不正确.
9.C 在△ABC和△DEB中,
∴△ABC≌△DEB,(SSS)
∴∠ACB=∠DBE.
∵∠AFB是△BCF的外角,
∴∠ACB+∠DBE=∠AFB,
∴∠ACB=∠AFB.
故选C.
10.D ∵BE⊥AC于点E,CF⊥AB于点F,
∴∠AEB=∠AFC=90°.
又∵∠A=∠A,AB=AC,
∴△ABE≌△ACF,故①正确,
∴AE=AF,∴BF=CE.
又∵BE⊥AC,CF⊥AB,∠BDF=∠CDE,
∴△BDF≌△CDE,故②正确,
∴DF=DE.
连接AD,
∵DE⊥AC,DF⊥AB,DE=DF,
∴点D在∠BAC的平分线上,故③正确.
故选D.
11.75° 由题意,得∠B=30°,∠A=45°.
∵∠1=90°,
∴∠A+∠3=90°,
∴∠3=45°,
∴∠4=45°.
∵∠B=30°,
∴∠2=45°+30°=75°.
12.≤k≤3 ∵y=k(x-1),∴当x=1时,y=0,即直线y=kx-k过定点(1,0).
∵直线y=kx-k(k≠0)与线段AB有交点,
∴当直线y=kx-k过点B(4,7)时,k值最小,则4k-k=7,解得k=;当直线y=kx-k过点A(2,3)时,k值最大,则2k-k=3,解得k=3,
∴k的取值范围为≤k≤3.
13.(-1,2) ∵直线y=2x+4与y轴交于点B,当x=0时,y=4,∴B(0,4).
∵以OB为边在y轴右侧作等边三角形OBC,
∴点C在线段OB的垂直平分线上,
∴点C的纵坐标为2.
将y=2代入y=2x+4,得2=2x+4,解得x=-1.故答案为(-1,2).
14.45°或135° 分两种情况:
(1)当∠ABC为锐角时,如图图①,
∵AD⊥BC,BE⊥AC,
∴∠BDM=∠ADC=90°.
∵∠AME=∠BMD,
∴∠MBD=∠CAD.
在△BMD和△ACD中,∵
∴△BMD≌△ACD,
∴AD=BD,
∴∠ABC=45°;
(2)当∠ABC为钝角时,如图图②,
∵AD⊥BC,BE⊥AC,
∴∠BDM=∠ADC=∠BEC=90°.
∵∠DBM=∠EBC,
∴∠M=∠C.
在△BMD和△ACD中,
∵
∴△BMD≌△ACD,
∴AD=BD,
∴∠ABD=45°,则∠ABC=135°.
综上所述,∠ABC=45°或∠ABC=135°.
15.解:如图图所示.
16.解:(1)△A1B1C1如图图所示,C1(-2,-1).
(2)△A2B2C2如图图所示,C2(2,4).
17.解:(1)证明:过点A作AF∥MD,如图图,
∴∠MBA+∠BAF=180°.
又∵∠MBA+∠BAC+∠NCA=360°,
∴∠FAC+∠NCA=180°,
∴AF∥NE,
∴MD∥NE.
(2)过点P作PQ∥MD,如图图.
∵BP和CP分别平分∠ABD,∠ACE,
∴∠DBP=∠ABD=×70°=35°,
∠PCE=∠ACE=×36°=18°.
∵PQ∥MD,
∴∠DBP=∠BPQ=35°.
∵MD∥NE,PQ∥MD,∴PQ∥NE,
∴∠QPC=∠PCE=18°,
∴∠BPC=∠BPQ+∠QPC=53°.
18.解:(1)证明:∵CD是AB的垂直平分线,
∴AC=BC,易得∠ACD=∠BCD.
又∵DE⊥AC,DF⊥BC,∴DE=DF.
(2)∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,∵
∴Rt△ADE≌Rt△BDF,(HL)
∴AE=BF.
∵CE=3 cm,BC=4 cm,
∴BF=AE=AC-CE=BC-CE=1 cm.
19.解:(1)如图图.
(2)猜想:y是x的一次函数.
设y=kx+b,把点(7,90),(8,80)代入,得
解得
∴y=-10x+160.
验证:点(9,70),(10,60)均在直线y=-10x+160上,
∴y与x之间的函数表达式为y=-10x+160.
(3)∵当x=12时,y=40,
∴估计12月份的测试中小明的数学成绩是40分.建议略.
20.解:(1)90° (2)60°
(3)∠BOC=2x.
证明:∵△ABM,△ACN都是以A为顶角的顶点的等腰三角形,
∴AB=AM,AC=AN.
由∠ANC=∠ABM,易得∠CAN=∠BAM,
∴∠CAN-∠BAC=∠BAM-∠BAC,
即∠BAN=∠MAC.
在△ABN和△AMC中,
∵
∴△ABN≌△AMC,(SAS)
∴∠ABN=∠AMC.
∵∠ANC=∠ABM=x,
∴∠BMO=∠AMC-x,∠NBM=∠ABN+x.
由三角形的外角性质,得∠NBM=∠BOC+∠BMO,
即∠ABN+x=∠BOC+∠AMC-x,
∴∠BOC=2x.
21.解:(1)由函数图象得B地到A地的距离是400米.
∵乐乐从B地跑步到A地,休息1分钟后接到通知,
∴a=3-1=2,
∴乐乐去A地的速度为400÷2=200(米/分).
故答案为2,200米/分.
(2)设线段FG的函数表达式为s=kt+b(k≠0).
∵s=kt+b(k≠0)的图象过点F(3,0),G(7,1200),
∴
解得
∴线段FG的函数表达式为s=300t-900(3≤t≤7),
即乐乐从A地到C地时s关于t的函数表达式为s=300t-900(3≤t≤7).
(3)男男从A地到C地的速度为1200÷8=150(米/分).
从A地到C地的速度为1200÷(7-3)=300(米/分).
①当0≤t≤2时,
200t=400-150t,
解得t=;
②当2400=150t-400,
解得t=>3,不合题意,舍去;
③当3≤t≤7时,
400-(300t-900)=150t-400或(300t-900)-400=150t-400,
解得t=或t=6;
④当t=8时,两人距B地的距离相等.
综上,两人距B地的距离相等的时间为分钟或分钟或6分钟或8分钟.
22.解:(1)证明:∵∠BAP+∠CAP=∠BAC=90°,∠CAQ+∠CAP=∠PAQ=90°,
∴∠BAP=∠CAQ.
在△ABP和△ACQ中,∵
∴△ABP≌△ACQ,(SAS)∴∠ACQ=∠B.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCQ=∠ACB+∠ACQ=∠ACB+∠B=45°+45°=90°,
∴CQ⊥BC.
(2)△ACQ能是直角三角形.
当∠APB=90°时,P为BC的中点,
当∠BAP=90°时,点P与点C重合.
∵△ABP≌△ACQ,
∴当P为BC的中点或与点C重合时,△ACQ是直角三角形.
(3)P为BC的中点或与点C重合或BP=AB.理由:
①当BP=AB时,△ABP是等腰三角形;
②当AB=AP,即P与点C重合时,△ABP为等腰三角形;
③当AP=BP,即P为BC的中点时,△ABP为等腰三角形.
∵△ABP≌△ACQ,
∴当P为BC的中点或与点C重合或BP=AB时,△ACQ是等腰三角形.
23.解:(1)①当以AB为腰时,点C有3个;
②当以AB为底时,点C有1个,
故使△ABC为等腰三角形的点C有4个.
(2)AM+BN=MN.
理由:由已知可得OA=OB,∠AOM=90°-∠BON=∠OBN.
在△AOM和△OBN中,
∴△AOM≌△OBN,(AAS)∴AM=ON,OM=BN,
∴AM+BN=ON+OM=MN.
(3)①当k>1时,如图图(a),AM=BN+MN.
∵∠AOB=∠BNO=∠AMO=90°,
∴∠BON+∠AON=90°,∠AON+∠OAM=90°,
∴∠BON=∠OAM.
在△AOM和△OBN中,
∴△AOM≌△OBN,(AAS)
∴BN=OM,ON=AM,∴AM=BN+MN.
②当k=1时,如图图(b),AM=BN,MN=0,
即AM=BN+MN.
③同理:当0
[时间:120分钟 分值:150分]
第Ⅰ卷 (选择题 共40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知点P的坐标为(-2,a2+1),则点P一定在 ( )
A.第一象限或第三象限 B.第二象限或第四象限
C.第二象限 D.第三象限
2.若将点P(1,-m)向右平移2个单位,再向上平移1个单位得到点Q(n,3),则点(m,n)的坐标为
( )
A.(3,-2) B.(2,-3) C.(3,2) D.(-2,3)
3.下列图形中,不是轴对称图形的是 ( )
A.①⑤ B.②⑤ C.④⑤ D.①②
4.已知不等边三角形的两边长分别是2 cm和9 cm,如图果第三边的长为整数,那么第三边的长为 ( )
A.8 cm B.10 cm C.8 cm或10 cm D.8 cm或9 cm
5.关于一次函数y=-2x+1,下列结论中不正确的是 ( )
A.图象经过点(1,-1) B.图象与两坐标轴围成的三角形的面积为
C.y随x的增大而减小 D.当x<时,y>0
6.在下列一组图形中,全等的三角形是 ( )
A.①和⑥ B.②和④,③和⑤
C.③和⑤ D.②和④
7.是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是 ( )
A.△ABD≌△ACD B.AF垂直平分EG
C.直线BG,CE的交点在AF上 D.△DEG是等边三角形
8.某通信公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.有下列结论:①如图描述的收费方式是方式1;②若月通话时间少于240分钟,选择方式2省钱;③若月通信费为50元,则方式1比方式2的通话时间多;④若方式1比方式2的通信费多10元,则方式1比方式2的通话时间多100分钟.其中正确的是
( )
A.①② B.③④ C.①②③ D.①②③④
9.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=DB,AB=DE,BC=EB,则∠ACB等于 ( )
A.∠EDB B.∠BED C.∠AFB D.2∠ABF
10.如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,有以下结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.其中正确的是( )
A.① B.② C.①② D.①②③
第Ⅱ卷 (非选择题 共110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一副三角尺按放置,若∠1=90°,则∠2的度数为 .
12.在平面直角坐标系中,已知点A(2,3),B(4,7),直线y=kx-k(k≠0)与线段AB有交点,则k的取值范围为 .
13.如图,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C'恰好落在直线AB上,则点C'的坐标为 .
14.△ABC的高AD,BE所在的直线交于点M,若BM=AC,则∠ABC的度数为 .
三、解答题(本大题共2小题,每小题8分,满分16分)
15.如图,在△ABC中,∠BAC是钝角,按要求完成下列画图(不写作法,保留作图痕迹):
①用尺规作∠BAC的平分线AE;
②用三角尺作AC边上的高BD;
③用尺规作AB边上的垂直平分线MN.
16.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-2,1),C(-2,4).
(1)画出△ABC沿着y轴向下平移5个单位得到的△A1B1C1,并直接写出点C的对应点C1的坐标;
(2)画出△ABC关于y轴对称的△A2B2C2,并直接写出点C的对应点C2的坐标.
四、解答题(本大题共2小题,每小题8分,满分16分)
17.如图,已知∠MBA+∠BAC+∠NCA=360°.
(1)求证:MD∥NE;
(2)若∠ABD=70°,∠ACE=36°,BP和CP分别平分∠ABD,∠ACE,求∠BPC的度数.
18.如图,已知CD是AB的垂直平分线,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)若线段CE的长为3 cm,BC的长为4 cm,求BF的长.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.小明平时喜欢玩游戏,本学期学校组织的几次数学反馈性测试,小明的数学成绩如图下表:
月份x(月) 7 8 9 10
成绩y(分) 90 80 70 60
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在如图所示的平面直角坐标系中描点并连线;
(2)观察(1)中所描点的位置关系,照这样的发展趋势,猜想y与x之间的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉迷于游戏中,照这样的发展趋势,请你估计12月份的测试中小明的数学成绩,并用一句话对小明提出一些建议.
20.如图所示,已知△ABC,分别以AB,AC为腰,以A为顶角的顶点作等腰三角形ABM、等腰三角形ACN,且∠ANC=∠ABM=x,MC与NB的延长线交于点O.
(1)如图图①,若x=45°,则∠O的度数为 ;
(2)如图图②,若x=30°,则∠O的度数为 ;
(3)如图图③,猜想∠BOC的度数(用含x的式子表示),并证明你的结论.
六、解答题(本题12分)
21.在一条笔直的道路上依次有A,B,C三地,男男从A地跑步到C地,同时乐乐从B地跑步到A地,休息1分钟后接到通知,要求乐乐比男男早1分钟到达C地,乐乐立即以比原来快的速度前往C地,两人均匀速运动,如图是男男跑步时间t(分)与两人距A地的距离s(米)之间的函数图象.
(1)a= ,乐乐去A地的速度为 ;
(2)结合图象,求出乐乐从A地到C地时s关于t的函数表达式(写出自变量的取值范围);
(3)请直接写出两人距B地的距离相等的时间.
七、解答题(本题12分)
22.如图,在△ABC中,AB=AC,∠BAC=90°,P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ,PQ,PQ与AC交于点H.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形 若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上的什么位置时,△ACQ是等腰三角形 请说明理由.
八、解答题(本题14分)
23.平面直角坐标系xOy中,已知定点A(1,0)和B(0,1).
(1)如图①,若动点C在x轴上运动,则使△ABC为等腰三角形的点C有几个
(2)过点A,B向直线l:y=-2x作垂线,垂足分别为M,N(如图图②),试判断线段AM,BN,MN之间的数量关系,并说明理由;
(3)过点A,B向动直线l:y=kx(k>0)作垂线,垂足分别为M,N,请直接写出线段AM,BN,MN之间的数量关系.
答案
期末综合提升卷
1.C
2.D 由题意可得n=1+2=3,3=-m+1,则m=-2.故点(m,n)的坐标为(-2,3).故选D.
3.A 根据轴对称的定义判断,①⑤不是轴对称图形.
4.C 根据三角形的三边关系,得7 cm<第三边长<11 cm,故第三边长为8 cm或9 cm或10 cm.
又∵三角形为不等边三角形,∴第三边长不能为9 cm.故选C.
5.B A项,当x=1时,y=-1,∴图象过点(1,-1),故正确,不符合题意;
B项,∵图象与坐标轴交于点,0和(0,1),
∴图象与两坐标轴围成的三角形的面积为,故不正确,符合题意;
C项,∵-2<0,∴y随x的增大而减小,故正确,不符合题意;
D项,∵当x<时,图象在x轴上方,∴y>0,故正确,不符合题意.故选B.
6.D ①⑥只有两个对应角相等,没有对应边相等,不符合条件;②④由两个对应角与这两个角的夹边相等,符合判定两个三角形全等的基本事实ASA;③⑤只有两个对应角相等,没有对应边相等,不符合条件.故选D.
7.D 由轴对称的性质,易知DE=DG,只有当∠EDG=60°或EG=DG时,△DEG才是等边三角形,故D项不一定成立.
8.C 根据题意,得方式1的函数表达式为y1=0.1x+20,方式2的函数表达式为y2=
①当x=80时,方式1的收费是28元,故①正确.
②0.1x+20>0.15x+8,解得x<240,故②正确.
③当y=50时,0.1x+20=50,解得x=300,0.15x+8=50,解得x=280,故③正确.
④当x≤80时,y2=20,令y1=0.1x+20=20+10,解得x=100,不符合方式1比方式2的通话时间多100分钟.
当x>80时,根据题意可得方程组解得符合题意.因此,当方式1比方式2的通信费多10元时,方式1不一定比方式2的通话时间多100分钟,故④不正确.
9.C 在△ABC和△DEB中,
∴△ABC≌△DEB,(SSS)
∴∠ACB=∠DBE.
∵∠AFB是△BCF的外角,
∴∠ACB+∠DBE=∠AFB,
∴∠ACB=∠AFB.
故选C.
10.D ∵BE⊥AC于点E,CF⊥AB于点F,
∴∠AEB=∠AFC=90°.
又∵∠A=∠A,AB=AC,
∴△ABE≌△ACF,故①正确,
∴AE=AF,∴BF=CE.
又∵BE⊥AC,CF⊥AB,∠BDF=∠CDE,
∴△BDF≌△CDE,故②正确,
∴DF=DE.
连接AD,
∵DE⊥AC,DF⊥AB,DE=DF,
∴点D在∠BAC的平分线上,故③正确.
故选D.
11.75° 由题意,得∠B=30°,∠A=45°.
∵∠1=90°,
∴∠A+∠3=90°,
∴∠3=45°,
∴∠4=45°.
∵∠B=30°,
∴∠2=45°+30°=75°.
12.≤k≤3 ∵y=k(x-1),∴当x=1时,y=0,即直线y=kx-k过定点(1,0).
∵直线y=kx-k(k≠0)与线段AB有交点,
∴当直线y=kx-k过点B(4,7)时,k值最小,则4k-k=7,解得k=;当直线y=kx-k过点A(2,3)时,k值最大,则2k-k=3,解得k=3,
∴k的取值范围为≤k≤3.
13.(-1,2) ∵直线y=2x+4与y轴交于点B,当x=0时,y=4,∴B(0,4).
∵以OB为边在y轴右侧作等边三角形OBC,
∴点C在线段OB的垂直平分线上,
∴点C的纵坐标为2.
将y=2代入y=2x+4,得2=2x+4,解得x=-1.故答案为(-1,2).
14.45°或135° 分两种情况:
(1)当∠ABC为锐角时,如图图①,
∵AD⊥BC,BE⊥AC,
∴∠BDM=∠ADC=90°.
∵∠AME=∠BMD,
∴∠MBD=∠CAD.
在△BMD和△ACD中,∵
∴△BMD≌△ACD,
∴AD=BD,
∴∠ABC=45°;
(2)当∠ABC为钝角时,如图图②,
∵AD⊥BC,BE⊥AC,
∴∠BDM=∠ADC=∠BEC=90°.
∵∠DBM=∠EBC,
∴∠M=∠C.
在△BMD和△ACD中,
∵
∴△BMD≌△ACD,
∴AD=BD,
∴∠ABD=45°,则∠ABC=135°.
综上所述,∠ABC=45°或∠ABC=135°.
15.解:如图图所示.
16.解:(1)△A1B1C1如图图所示,C1(-2,-1).
(2)△A2B2C2如图图所示,C2(2,4).
17.解:(1)证明:过点A作AF∥MD,如图图,
∴∠MBA+∠BAF=180°.
又∵∠MBA+∠BAC+∠NCA=360°,
∴∠FAC+∠NCA=180°,
∴AF∥NE,
∴MD∥NE.
(2)过点P作PQ∥MD,如图图.
∵BP和CP分别平分∠ABD,∠ACE,
∴∠DBP=∠ABD=×70°=35°,
∠PCE=∠ACE=×36°=18°.
∵PQ∥MD,
∴∠DBP=∠BPQ=35°.
∵MD∥NE,PQ∥MD,∴PQ∥NE,
∴∠QPC=∠PCE=18°,
∴∠BPC=∠BPQ+∠QPC=53°.
18.解:(1)证明:∵CD是AB的垂直平分线,
∴AC=BC,易得∠ACD=∠BCD.
又∵DE⊥AC,DF⊥BC,∴DE=DF.
(2)∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,∵
∴Rt△ADE≌Rt△BDF,(HL)
∴AE=BF.
∵CE=3 cm,BC=4 cm,
∴BF=AE=AC-CE=BC-CE=1 cm.
19.解:(1)如图图.
(2)猜想:y是x的一次函数.
设y=kx+b,把点(7,90),(8,80)代入,得
解得
∴y=-10x+160.
验证:点(9,70),(10,60)均在直线y=-10x+160上,
∴y与x之间的函数表达式为y=-10x+160.
(3)∵当x=12时,y=40,
∴估计12月份的测试中小明的数学成绩是40分.建议略.
20.解:(1)90° (2)60°
(3)∠BOC=2x.
证明:∵△ABM,△ACN都是以A为顶角的顶点的等腰三角形,
∴AB=AM,AC=AN.
由∠ANC=∠ABM,易得∠CAN=∠BAM,
∴∠CAN-∠BAC=∠BAM-∠BAC,
即∠BAN=∠MAC.
在△ABN和△AMC中,
∵
∴△ABN≌△AMC,(SAS)
∴∠ABN=∠AMC.
∵∠ANC=∠ABM=x,
∴∠BMO=∠AMC-x,∠NBM=∠ABN+x.
由三角形的外角性质,得∠NBM=∠BOC+∠BMO,
即∠ABN+x=∠BOC+∠AMC-x,
∴∠BOC=2x.
21.解:(1)由函数图象得B地到A地的距离是400米.
∵乐乐从B地跑步到A地,休息1分钟后接到通知,
∴a=3-1=2,
∴乐乐去A地的速度为400÷2=200(米/分).
故答案为2,200米/分.
(2)设线段FG的函数表达式为s=kt+b(k≠0).
∵s=kt+b(k≠0)的图象过点F(3,0),G(7,1200),
∴
解得
∴线段FG的函数表达式为s=300t-900(3≤t≤7),
即乐乐从A地到C地时s关于t的函数表达式为s=300t-900(3≤t≤7).
(3)男男从A地到C地的速度为1200÷8=150(米/分).
从A地到C地的速度为1200÷(7-3)=300(米/分).
①当0≤t≤2时,
200t=400-150t,
解得t=;
②当2
解得t=>3,不合题意,舍去;
③当3≤t≤7时,
400-(300t-900)=150t-400或(300t-900)-400=150t-400,
解得t=或t=6;
④当t=8时,两人距B地的距离相等.
综上,两人距B地的距离相等的时间为分钟或分钟或6分钟或8分钟.
22.解:(1)证明:∵∠BAP+∠CAP=∠BAC=90°,∠CAQ+∠CAP=∠PAQ=90°,
∴∠BAP=∠CAQ.
在△ABP和△ACQ中,∵
∴△ABP≌△ACQ,(SAS)∴∠ACQ=∠B.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCQ=∠ACB+∠ACQ=∠ACB+∠B=45°+45°=90°,
∴CQ⊥BC.
(2)△ACQ能是直角三角形.
当∠APB=90°时,P为BC的中点,
当∠BAP=90°时,点P与点C重合.
∵△ABP≌△ACQ,
∴当P为BC的中点或与点C重合时,△ACQ是直角三角形.
(3)P为BC的中点或与点C重合或BP=AB.理由:
①当BP=AB时,△ABP是等腰三角形;
②当AB=AP,即P与点C重合时,△ABP为等腰三角形;
③当AP=BP,即P为BC的中点时,△ABP为等腰三角形.
∵△ABP≌△ACQ,
∴当P为BC的中点或与点C重合或BP=AB时,△ACQ是等腰三角形.
23.解:(1)①当以AB为腰时,点C有3个;
②当以AB为底时,点C有1个,
故使△ABC为等腰三角形的点C有4个.
(2)AM+BN=MN.
理由:由已知可得OA=OB,∠AOM=90°-∠BON=∠OBN.
在△AOM和△OBN中,
∴△AOM≌△OBN,(AAS)∴AM=ON,OM=BN,
∴AM+BN=ON+OM=MN.
(3)①当k>1时,如图图(a),AM=BN+MN.
∵∠AOB=∠BNO=∠AMO=90°,
∴∠BON+∠AON=90°,∠AON+∠OAM=90°,
∴∠BON=∠OAM.
在△AOM和△OBN中,
∴△AOM≌△OBN,(AAS)
∴BN=OM,ON=AM,∴AM=BN+MN.
②当k=1时,如图图(b),AM=BN,MN=0,
即AM=BN+MN.
③同理:当0
同课章节目录
