人教版数学八年级上册同步提优训练:13.4 课题学习 最短路径问题(word、含答案)
文档属性
| 名称 | 人教版数学八年级上册同步提优训练:13.4 课题学习 最短路径问题(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 481.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 12:42:38 | ||
图片预览




文档简介
13.4 课题学习 最短路径问题
命题点1 两定点在直线同侧的“两定一动”
1.如图,直线l是一条河,P,Q是两个村庄.欲在直线l上的某处修建一个水泵站M,向P,Q两村供水,现有如图下四种铺设方案,图中PM,MQ表示铺设的管道,则所需管道最短的是 ( )
2.如图,在△ABC中,AB=6,AC=8,BC=10,EF是BC的垂直平分线,P是直线EF上的一动点,则PA+PB的最小值是 ( )
A.6 B.8 C.10 D.14
3.[2020·武汉武昌区期中] 如图,△ABC为等边三角形,D,E分别是AC,BC的中点,F是BD上的一个动点,当CF+EF取到最小值时,∠FCB的度数是 ( )
A.22.5° B.25° C.30° D.45°
4.[2020·大连中山区期中] 如图,在平面直角坐标系中,A(0,2),B(4,2),点P是x轴上任意一点,当PA+PB有最小值时,点P的坐标为 ( )
A.(0,0) B.(1,0) C.(2,0) D.(3,0)
5.如图,等腰三角形ABC的底边BC的长为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )
A.8 B.10 C.12 D.14
6. 如图,已知△ABC为等边三角形,高AH=8 cm,P为AH上一动点,D为AB的中点,则PD+PB的最小值为 cm.
7.如图,在河岸l的同侧有两个居民小区A,B,现欲在河岸边建一个长为a的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.在图中画出绿化带的位置,并写出画图过程.
8.如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货栈D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.试问在公路边是否存在一点D,使送货路线之和最短 若存在,请在图中画出点D所在的位置,并简要说明作法;若不存在,请说明理由.
9.河的两岸成平行线,A,B是位于河两岸的两个车间(如图),要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法是:作从A到河岸的垂线,分别交河岸PQ,MN于点F,G.在AG上取AE=FG,连接EB交MN于点D.在点D处作到对岸的垂线DC,垂足为C,那么CD就是造桥的位置.请说出桥造在CD位置时路程最短的理由,也就是AC+CD+DB最短的理由.
命题点2 一定点两动点型
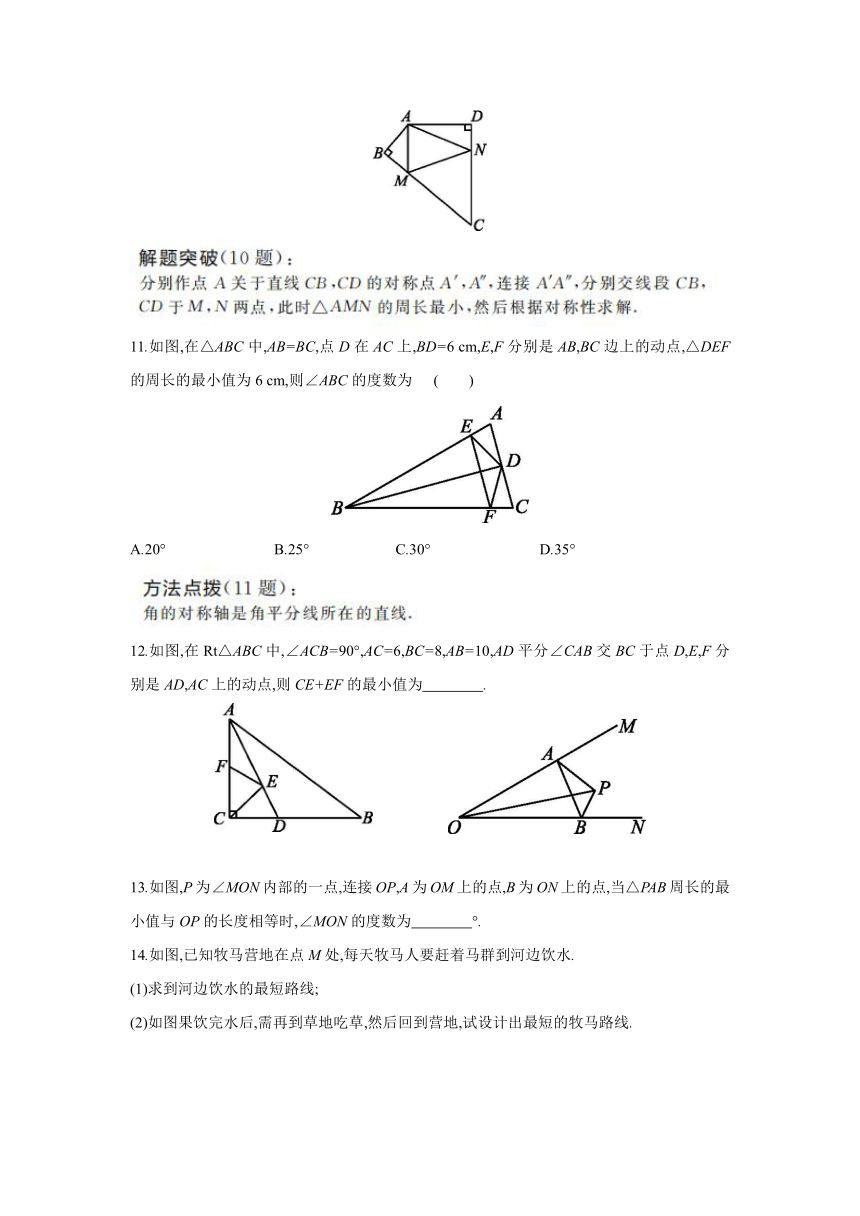
10.如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则此时∠AMN+∠ANM的度数为 ( )
A.80° B.90° C.100° D.130°
11.如图,在△ABC中,AB=BC,点D在AC上,BD=6 cm,E,F分别是AB,BC边上的动点,△DEF的周长的最小值为6 cm,则∠ABC的度数为 ( )
A.20° B.25° C.30° D.35°
12.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD平分∠CAB交BC于点D,E,F分别是AD,AC上的动点,则CE+EF的最小值为 .
13.如图,P为∠MON内部的一点,连接OP,A为OM上的点,B为ON上的点,当△PAB周长的最小值与OP的长度相等时,∠MON的度数为 °.
14.如图,已知牧马营地在点M处,每天牧马人要赶着马群到河边饮水.
(1)求到河边饮水的最短路线;
(2)如图果饮完水后,需再到草地吃草,然后回到营地,试设计出最短的牧马路线.
15.如图,某护城河在C和C'处直角转弯,河宽均相等,从A处到达B处,须经两座桥DD',EE'(桥宽不计),设护城河以及两座桥都是东西或南北走向的,请设计出架桥路线,使ADD'E'EB的长最短.
答案
1.D
2.B 如图图,连接BE,
∵EF是BC的垂直平分线,∴BE=CE.
根据两点之间线段最短,可知PA+PB=PA+PC=AC时最小,此时点P与点E重合.
∴PA+PB的最小值即为AC的长.
∵AC=8,∴PA+PB的最小值为8.
3.C ∵△ABC为等边三角形,D,E分别是AC,BC的中点,
∴BD⊥AC.∴点C与点A关于BD对称.连接AE交BD于点F,如图图,则此时CF+EF的值最小.
∵BD垂直平分AC,∴AF=CF.
∵△ABC是等边三角形,E是BC的中点,
∴∠CAE=∠BAC=30°,AE⊥BC.
∴∠ACF=∠CAF=30°,∠AEC=90°.
∴∠FCB=∠ACB-∠ACF=30°.
4.C 作点A关于x轴的对称点A',连接BA'与x轴交于点P',作BC⊥x轴于点C,则PA+PB的最小值就是线段A'B的值.
∵A(0,2),B(4,2),
∴点A'的坐标为(0,-2).OA'=BC.
在△OA'P'和△CBP'中,
∴△OA'P'≌△CBP'(AAS).
∴OP'=CP'.
∵OC=4,∴OP'=2.
∴点P'的坐标为(2,0).
5.D 如图图,连接AD,MA.
∵△ABC是等腰三角形,D是BC边的中点,
∴AD⊥BC.
∴S△ABC=BC·AD=×4AD=24,
解得AD=12.
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC.
∴MC+DM=MA+DM≥AD.
∴AD的长为MC+MD的最小值.
∴△CDM的周长的最小值为(MC+MD)+CD=AD+BC=12+×4=14.故选D.
6.8 如图图,
∵△ABC是等边三角形,∴点D关于AH的对称点D'在AC上,连接BD',交AH于点P,此时PD+PB的值最小,PD+PB=PD'+PB=BD'.
∵△ABC为等边三角形,D是AB的中点,
∴D'是AC的中点.
∴BD'=AH=8 cm.故答案为8.
7.解:如图图,作线段AP∥l,使AP=a,且点P在点A的右侧;作点P关于直线l的对称点P',连接BP'交l于点D;在l上点D的左侧截取DC=a,则CD就是所求绿化带的位置.
8.解:存在.如图图,作点A关于x轴的对称点A',连接A'C,则A'C与x轴的交点即为点D.
9.解:利用图形平移的性质及“两点的所有连线中,线段最短”,可知:AC+CD+DB=(ED+DB)+CD=EB+CD.而CD的长度又是平行线PQ与MN之间的距离,所以AC+CD+DB最短.
10.C 如图图,延长AB到点A',使得BA'=BA,延长AD到点A″,使得DA″=AD,连接A'A″与BC,CD分别交于点M,N.
∵∠ABC=∠ADC=90°,
∴点A,A'关于BC对称,点A,A″关于CD对称,此时△AMN的周长最小.
∵BA=BA',MB⊥AB,
∴MA=MA'.
同理NA=NA″.
∴∠A'=∠MAB,∠A″=∠NAD.
∵∠AMN=∠A'+∠MAB=2∠A',∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A'+∠A″).
∵∠BAD=130°,
∴∠A'+∠A″=180°-∠BAD=50°.
∴∠AMN+∠ANM=2×50°=100°.
11.C 如图图,
将△ABD和△DBC分别沿着AB和BC向外翻折,得△ABG和△HBC,
连接GH,分别交AB,BC于点E,F,
此时△DEF的周长最小,即为GH的长.
∵△DEF周长的最小值为6 cm,
∴GH=6 cm.
∵BD=6 cm,∴BG=BH=BD=6 cm=GH.
∴△BGH是等边三角形.
∴∠GBH=60°.
∴2∠ABD+2∠DBC=60°.
∴∠ABD+∠DBC=30°.
∴∠ABC=30°.故选C.
12. 如图图,在AB上取一点F',
使AF'=AF,过点C作CH⊥AB,垂足为H.
∵AD平分∠CAB,∴∠CAD=∠BAD.
在△AFE和△AF'E中,
∴△AFE≌△AF'E(SAS).∴EF=EF'.
∵S△ABC=AB·CH=AC·BC,
∴CH===.
∵CE+EF=CE+EF',
∴当C,E,F'共线,即点F'与点H重合时,CE+EF的值最小,最小值为.故答案为.
13.30 如图图,分别作点P关于直线OM,ON的对称点P1,P2,然后连接两个对称点即可得到A,B两点,则△PAB即为所求的三角形,此时△PAB的周长=P1P2.
根据对称性可知,∠AOP1=∠AOP,∠BOP=∠BOP2,OP1=OP2=OP.
∴∠P1OP2=2∠MON.
∵△PAB周长的最小值与OP的长度相等,
∴P1P2=OP.
∴OP1=OP2=P1P2.
∴△P1OP2是等边三角形.
∴∠P1OP2=60°,∴∠MON=30°.故答案为30.
14.解:把河流抽象成直线a,把草地抽象成直线b.
(1)如图图①,过点M作MP⊥直线a于点P,则MP即为最短路线.
(2)如图图②,分别作点M关于直线a,b的对称点A,B,连接AB与直线a,b分别交于点C,D,则最短的牧马路线为M→C→D→M.
15.解:过点A作河岸的垂线并向河岸方向截取AF=河宽,过点B作河岸的垂线并向河岸方向截取BG=河宽,连接GF,与河岸相交于点E',D'.作DD',EE'分别垂直于河岸,则 DD',EE'即为桥,即当桥建于如图图所示的位置时,ADD'E'EB的长最短.
命题点1 两定点在直线同侧的“两定一动”
1.如图,直线l是一条河,P,Q是两个村庄.欲在直线l上的某处修建一个水泵站M,向P,Q两村供水,现有如图下四种铺设方案,图中PM,MQ表示铺设的管道,则所需管道最短的是 ( )
2.如图,在△ABC中,AB=6,AC=8,BC=10,EF是BC的垂直平分线,P是直线EF上的一动点,则PA+PB的最小值是 ( )
A.6 B.8 C.10 D.14
3.[2020·武汉武昌区期中] 如图,△ABC为等边三角形,D,E分别是AC,BC的中点,F是BD上的一个动点,当CF+EF取到最小值时,∠FCB的度数是 ( )
A.22.5° B.25° C.30° D.45°
4.[2020·大连中山区期中] 如图,在平面直角坐标系中,A(0,2),B(4,2),点P是x轴上任意一点,当PA+PB有最小值时,点P的坐标为 ( )
A.(0,0) B.(1,0) C.(2,0) D.(3,0)
5.如图,等腰三角形ABC的底边BC的长为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )
A.8 B.10 C.12 D.14
6. 如图,已知△ABC为等边三角形,高AH=8 cm,P为AH上一动点,D为AB的中点,则PD+PB的最小值为 cm.
7.如图,在河岸l的同侧有两个居民小区A,B,现欲在河岸边建一个长为a的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.在图中画出绿化带的位置,并写出画图过程.
8.如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货栈D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D或D→C→B→A→D.试问在公路边是否存在一点D,使送货路线之和最短 若存在,请在图中画出点D所在的位置,并简要说明作法;若不存在,请说明理由.
9.河的两岸成平行线,A,B是位于河两岸的两个车间(如图),要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法是:作从A到河岸的垂线,分别交河岸PQ,MN于点F,G.在AG上取AE=FG,连接EB交MN于点D.在点D处作到对岸的垂线DC,垂足为C,那么CD就是造桥的位置.请说出桥造在CD位置时路程最短的理由,也就是AC+CD+DB最短的理由.
命题点2 一定点两动点型
10.如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小,则此时∠AMN+∠ANM的度数为 ( )
A.80° B.90° C.100° D.130°
11.如图,在△ABC中,AB=BC,点D在AC上,BD=6 cm,E,F分别是AB,BC边上的动点,△DEF的周长的最小值为6 cm,则∠ABC的度数为 ( )
A.20° B.25° C.30° D.35°
12.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AB=10,AD平分∠CAB交BC于点D,E,F分别是AD,AC上的动点,则CE+EF的最小值为 .
13.如图,P为∠MON内部的一点,连接OP,A为OM上的点,B为ON上的点,当△PAB周长的最小值与OP的长度相等时,∠MON的度数为 °.
14.如图,已知牧马营地在点M处,每天牧马人要赶着马群到河边饮水.
(1)求到河边饮水的最短路线;
(2)如图果饮完水后,需再到草地吃草,然后回到营地,试设计出最短的牧马路线.
15.如图,某护城河在C和C'处直角转弯,河宽均相等,从A处到达B处,须经两座桥DD',EE'(桥宽不计),设护城河以及两座桥都是东西或南北走向的,请设计出架桥路线,使ADD'E'EB的长最短.
答案
1.D
2.B 如图图,连接BE,
∵EF是BC的垂直平分线,∴BE=CE.
根据两点之间线段最短,可知PA+PB=PA+PC=AC时最小,此时点P与点E重合.
∴PA+PB的最小值即为AC的长.
∵AC=8,∴PA+PB的最小值为8.
3.C ∵△ABC为等边三角形,D,E分别是AC,BC的中点,
∴BD⊥AC.∴点C与点A关于BD对称.连接AE交BD于点F,如图图,则此时CF+EF的值最小.
∵BD垂直平分AC,∴AF=CF.
∵△ABC是等边三角形,E是BC的中点,
∴∠CAE=∠BAC=30°,AE⊥BC.
∴∠ACF=∠CAF=30°,∠AEC=90°.
∴∠FCB=∠ACB-∠ACF=30°.
4.C 作点A关于x轴的对称点A',连接BA'与x轴交于点P',作BC⊥x轴于点C,则PA+PB的最小值就是线段A'B的值.
∵A(0,2),B(4,2),
∴点A'的坐标为(0,-2).OA'=BC.
在△OA'P'和△CBP'中,
∴△OA'P'≌△CBP'(AAS).
∴OP'=CP'.
∵OC=4,∴OP'=2.
∴点P'的坐标为(2,0).
5.D 如图图,连接AD,MA.
∵△ABC是等腰三角形,D是BC边的中点,
∴AD⊥BC.
∴S△ABC=BC·AD=×4AD=24,
解得AD=12.
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC.
∴MC+DM=MA+DM≥AD.
∴AD的长为MC+MD的最小值.
∴△CDM的周长的最小值为(MC+MD)+CD=AD+BC=12+×4=14.故选D.
6.8 如图图,
∵△ABC是等边三角形,∴点D关于AH的对称点D'在AC上,连接BD',交AH于点P,此时PD+PB的值最小,PD+PB=PD'+PB=BD'.
∵△ABC为等边三角形,D是AB的中点,
∴D'是AC的中点.
∴BD'=AH=8 cm.故答案为8.
7.解:如图图,作线段AP∥l,使AP=a,且点P在点A的右侧;作点P关于直线l的对称点P',连接BP'交l于点D;在l上点D的左侧截取DC=a,则CD就是所求绿化带的位置.
8.解:存在.如图图,作点A关于x轴的对称点A',连接A'C,则A'C与x轴的交点即为点D.
9.解:利用图形平移的性质及“两点的所有连线中,线段最短”,可知:AC+CD+DB=(ED+DB)+CD=EB+CD.而CD的长度又是平行线PQ与MN之间的距离,所以AC+CD+DB最短.
10.C 如图图,延长AB到点A',使得BA'=BA,延长AD到点A″,使得DA″=AD,连接A'A″与BC,CD分别交于点M,N.
∵∠ABC=∠ADC=90°,
∴点A,A'关于BC对称,点A,A″关于CD对称,此时△AMN的周长最小.
∵BA=BA',MB⊥AB,
∴MA=MA'.
同理NA=NA″.
∴∠A'=∠MAB,∠A″=∠NAD.
∵∠AMN=∠A'+∠MAB=2∠A',∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A'+∠A″).
∵∠BAD=130°,
∴∠A'+∠A″=180°-∠BAD=50°.
∴∠AMN+∠ANM=2×50°=100°.
11.C 如图图,
将△ABD和△DBC分别沿着AB和BC向外翻折,得△ABG和△HBC,
连接GH,分别交AB,BC于点E,F,
此时△DEF的周长最小,即为GH的长.
∵△DEF周长的最小值为6 cm,
∴GH=6 cm.
∵BD=6 cm,∴BG=BH=BD=6 cm=GH.
∴△BGH是等边三角形.
∴∠GBH=60°.
∴2∠ABD+2∠DBC=60°.
∴∠ABD+∠DBC=30°.
∴∠ABC=30°.故选C.
12. 如图图,在AB上取一点F',
使AF'=AF,过点C作CH⊥AB,垂足为H.
∵AD平分∠CAB,∴∠CAD=∠BAD.
在△AFE和△AF'E中,
∴△AFE≌△AF'E(SAS).∴EF=EF'.
∵S△ABC=AB·CH=AC·BC,
∴CH===.
∵CE+EF=CE+EF',
∴当C,E,F'共线,即点F'与点H重合时,CE+EF的值最小,最小值为.故答案为.
13.30 如图图,分别作点P关于直线OM,ON的对称点P1,P2,然后连接两个对称点即可得到A,B两点,则△PAB即为所求的三角形,此时△PAB的周长=P1P2.
根据对称性可知,∠AOP1=∠AOP,∠BOP=∠BOP2,OP1=OP2=OP.
∴∠P1OP2=2∠MON.
∵△PAB周长的最小值与OP的长度相等,
∴P1P2=OP.
∴OP1=OP2=P1P2.
∴△P1OP2是等边三角形.
∴∠P1OP2=60°,∴∠MON=30°.故答案为30.
14.解:把河流抽象成直线a,把草地抽象成直线b.
(1)如图图①,过点M作MP⊥直线a于点P,则MP即为最短路线.
(2)如图图②,分别作点M关于直线a,b的对称点A,B,连接AB与直线a,b分别交于点C,D,则最短的牧马路线为M→C→D→M.
15.解:过点A作河岸的垂线并向河岸方向截取AF=河宽,过点B作河岸的垂线并向河岸方向截取BG=河宽,连接GF,与河岸相交于点E',D'.作DD',EE'分别垂直于河岸,则 DD',EE'即为桥,即当桥建于如图图所示的位置时,ADD'E'EB的长最短.
