人教版数学九年级上册同步提优训练:第二十三章 旋转 综合提升卷(word,含答案)
文档属性
| 名称 | 人教版数学九年级上册同步提优训练:第二十三章 旋转 综合提升卷(word,含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 759.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 00:00:00 | ||
图片预览





文档简介
第二十三章综合提升卷
范围:旋转 时间:90分钟 分值:100分第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
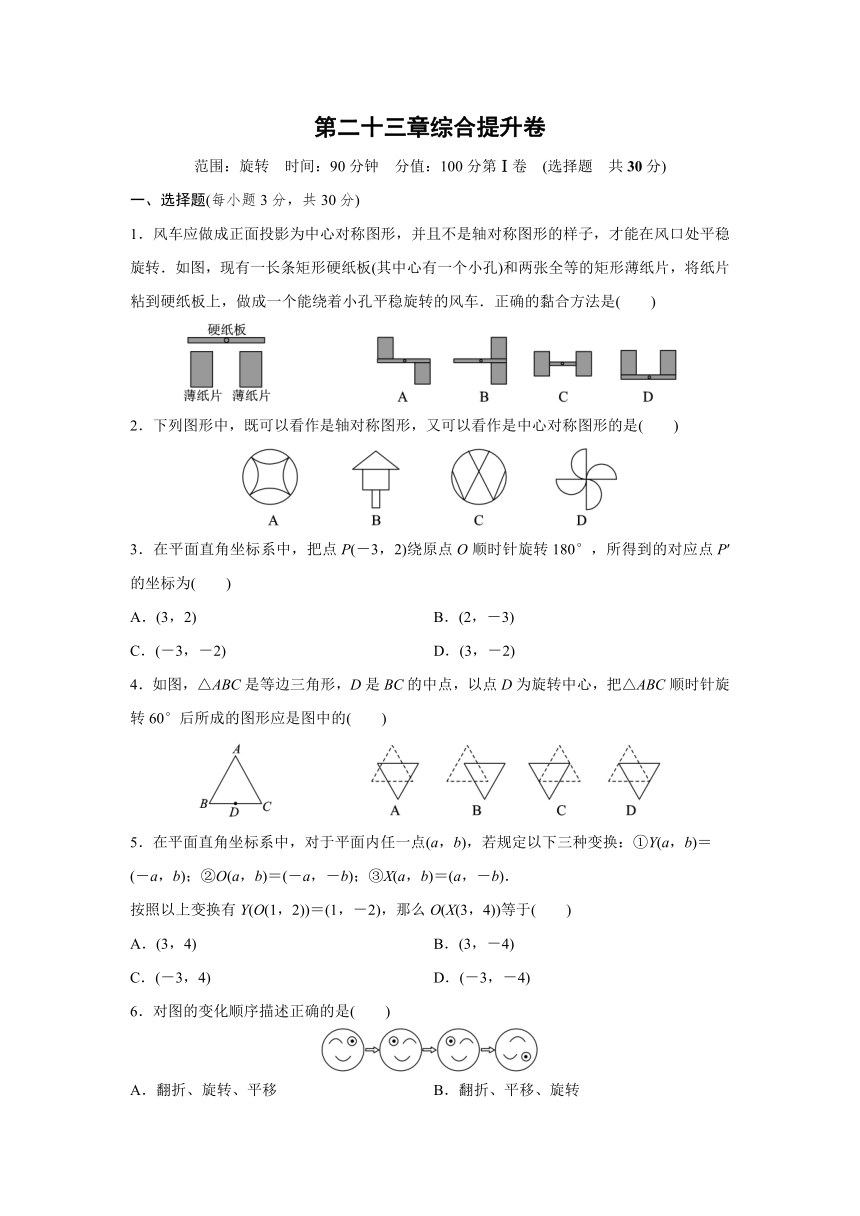
1.风车应做成正面投影为中心对称图形,并且不是轴对称图形的样子,才能在风口处平稳旋转.如图,现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的黏合方法是( )
2.下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的是( )
3.在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B.(2,-3)
C.(-3,-2) D.(3,-2)
4.如图,△ABC是等边三角形,D是BC的中点,以点D为旋转中心,把△ABC顺时针旋转60°后所成的图形应是图中的( )
5.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:①Y(a,b)=
(-a,b);②O(a,b)=(-a,-b);③X(a,b)=(a,-b).
按照以上变换有Y(O(1,2))=(1,-2),那么O(X(3,4))等于( )
A.(3,4) B.(3,-4)
C.(-3,4) D.(-3,-4)
6.对图的变化顺序描述正确的是( )
A.翻折、旋转、平移 B.翻折、平移、旋转
C.平移、翻折、旋转 D.旋转、翻折、平移
7.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5) B.(1,0)
C.(1,-1) D.(1.5,-0.5)
8.如图,已知在 ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的度数为( )
A.130° B.150°
C.160° D.170°
9.如图,在△ABC中,AC=6 ,∠A=45°,∠B=30°,P是BC边上一点,将PC绕着点P逆时针旋转得到PC′,旋转角为α(0°<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包括边上),则PC长的取值范围是( )
A.0<PC<4 B.4<PC<6 C.0<PC<6 D.0<PC<4
10.一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如图下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形.例如图:若第一个正六边形下面标的数字为2,如图①,则先绕其中心顺时针旋转2格,再沿直线l翻折,得到第二个图形.若第一个正六边形下面标的数字为4,直线l的位置如图②所示,按照游戏规则,得到的第二个图形应是( )
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题3分,共18分)
11.如图,该图形可以看作是由一个“”每次旋转________得到的.
12.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是________.
13.已知点P(a+1,2a-3)关于原点的对称点在第二象限,则a的取值范围是______________.
14.如图,在平面直角坐标系中,四边形OABC与四边形CDEF都是正方形,OA=2,M,D分别是AB,BC的中点,当把正方形CDEF绕点C旋转某个角度或沿y轴上下平移后,若点F的对应点为F′,且OF′=OM,则点F′的坐标是__________________.
15.如图,菱形ABCD和菱形AEFG开始时互相重合,现将菱形AEFG绕点A顺时针旋转,设旋转角∠BAE=α(0°<α<360°),则当α=______________时,菱形AEFG的顶点F会落在菱形ABCD的对角线AC或BD所在的直线上.
16.如图是一个坐标方格盘,你可操纵一只遥控机器蛙在方格盘上进行跳步游戏,机器蛙每次跳步只能按如图下两种方式:第一种,向上、下、左、右可任意跳动1格或3格;第二种,跳到关于原点的对称点上.若机器蛙在点A(-5,4)处,现欲操纵它跳到点B(2,-3)处,则机器蛙至少要跳________次.
三、解答题(共52分)
17.(5分)如图①是利用正方形各边中点和弧的中点设计的正方形瓷砖图案,用四块如图①所示的正方形瓷砖拼成一个新的正方形图案,使拼成的图案既是轴对称图形,又是中心对称图形.请你在图②和图③中各画一种拼法(要求两种拼法不相同).
18.(5分)用直尺和圆规作图(不写作法,保留作图痕迹):
已知:如图,△A′B′C′是由△ABC以点O为中心经过一次旋转得到的,点A′,B′,C′分别是点A,B,C旋转后的对应点.
求作:旋转中心O.
19.(5分)如图,△DEF是由△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说这些对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
20.(6分)如图,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接DC,已知∠DCB=30°.求证:DC2+BC2=AC2.
21.(7分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.
22.(7分)将抛物线C1:y=(x+1)2-2绕点P(t,2)旋转180°得到抛物线C2,若抛物线C1的顶点在抛物线C2上,同时抛物线C2的顶点在抛物线C1上,求抛物线C2的解析式.
23.(7分)在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA的延长线上(如图).
(1)求证:BB1∥CA1;
(2)求△AB1C的面积.
24.(10分)已知:在△ABC中,AB=4,AC=3,以CB为边作等边三角形CBP,连接AP,求AP的长.
这道题目难倒了小明,因为没有具体图形,发现△ABC不是一个固定的图形,也没有指定等边三角形CBP在BC所在直线的哪一侧,这两个不确定的因素会使得AP的长不一定是固定的,为此小明从特殊情况出发研究这个问题,按如图下步骤解决:
步骤1:取∠CAB=30°,以CB为边作等边三角形CBP,使点A与点P在BC所在直线的两侧;
步骤2:要想建立AB,AC,AP的联系,需要将这三条线段进行转移处理,由于图中有等边三角形,可以通过旋转来完成线段与角的转移,因此将△ACP以点P为旋转中心,逆时针旋转60°,得到△P′BP,通过推理与计算得到了此位置时AP的长.
(1)请结合小明的步骤在图中补全图形;
(2)结合(1)中补全后的图形求出此时AP的长;
(3)根据上述经验,改变∠CAB的度数,发现∠CAB在变化到某一角度时,AP的长有最大值,画出∠CAB为这个特殊角度时的示意图,写出AP长的最大值,并说明大致思路.
答案
1.A 可凭生活中的经验,也可以由风车的正面投影是中心对称图形,但不是轴对称图形进行判断.
2.A 选项B是轴对称图形,但不是中心对称图形;选项C是轴对称图形,但不是中心对称图形;选项D是中心对称图形,但不是轴对称图形;只有选项A既是中心对称图形,又是轴对称图形.
3.D 由题意可得,点P和点P′关于原点对称,它们的横、纵坐标分别互为相反数.
4.D
5.C 根据题意可得O(X(3,4))=O(3,-4)=(-3,4).故选C.
6.B
7.C 连接AA′,BB′,作BB′的垂直平分线,再作AA′的垂直平分线,两条直线相交于一点,此点即为旋转中心,坐标为(1,-1).
8.C 由四边形ABCD是平行四边形,
得AD∥BC.
又∵∠ADA′=50°,∴∠DA′E=130°.
易得∠E′A′B=∠EAB=30°,∴∠DA′E′=160°.
9.A 如图,过点C作CD⊥AB于点D,过点P作PH⊥AB于点H.
∵AC=6 ,∠A=45°,∠B=30°,
∴AD=CD=6,BC=2CD=12.
设PC=x=PC′,
则BP=12-x,PH=(12-x).
∵旋转过程中,点C′始终落在△ABC内部(不包括边上),∴PC′<PH,
即x<(12-x),解得x<4,即PC<4.
又∵PC>0,∴0<PC<4.
10.A 先绕其中心顺时针旋转4格:
再沿直线l翻折:
11.90° 12.3
13.-1<a< ∵点P关于原点的对称点在第二象限,∴点P在第四象限,
∴
解得∴-1<a<.
14.(0,)或(0,-)或(-1,2)或(1,2)
①若把正方形CDEF沿y轴上下平移,
∵OM==,
∴在y轴上点F有两个对应点,坐标分别为(0,),(0,-).
②若把正方形CDEF绕点C旋转某个角度,
连接OD,易证△OCD≌△OAM,∴OD=OM,则点D为点F的对应点,其坐标为(1,2);
在BC的延长线上点D关于y轴的对称点位置也存在一点F′,使OF′=OM,该点坐标为(-1,2).
15.60°或180°或300° 如图①,当点F在线段DB的延长线上时,∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC,∴∠AOF=90°.
∵AF=AC,∴OA=AF,
∴∠CAF=60°,即旋转角为60°;
如图②,当点F在线段CA的延长线上时,
∠CAF=180°,∴旋转角为180°;
如图③,当点F在线段BD的延长线上时,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC,
∴∠AOF=90°.
∵AF=AC,∴OA=AF,∴∠CAF=60°.
则旋转角为360°-60°=300°.
∴α=60°或180°或300°.
16.3 机器蛙在点A(-5,4)处,根据跳步游戏规则,可以先向右跳3格,再向下跳1格,然后跳到关于原点的对称点处,即可跳到点B(2,-3)处,故机器蛙至少要跳3次.
17.解:答案不唯一,如图:
18.解:如图所示:
19.解:(1)由图可知,点A(2,3),点D(-2,-3),点B(1,2),点E(-1,-2),点C(3,1),点F(-3,-1).
这些对应点的坐标特征:横、纵坐标分别互为相反数.
(2)由(1)可知a+3+2a=0,4-b+2b-3=0,解得a=-1,b=-1.
20.证明:连接EC.
∵将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,
∴△ABC≌△DBE,∴AC=DE,BC=BE.
又∵∠CBE=60°,∴△BCE是等边三角形,
∴EC=BC,∠BCE=60°.
又∵∠DCB=30°,∴∠DCE=90°,
∴DC2+EC2=DE2,∴DC2+BC2=AC2.
21.解:四边形ACFD是菱形.
理由:∵在Rt△ABC中,∠ACB=90°,∠B=30°,∴∠A=90°-∠B=60°,AC=AB.
∵将△ABC绕点C按顺时针方向旋转,得到△DEC,
∴AC=DC,AB=DE,∠ACB=∠DCE=90°,
∴△ACD是等边三角形,
∴AC=AD.
∵F是DE的中点,
∴DF=CF=DE,
∴AC=CF=DF=AD,∴四边形ACFD是菱形.
22.解:∵抛物线y=(x+1)2-2的顶点坐标为(-1,-2),
∴绕点P(t,2)旋转180°得到抛物线C2的顶点坐标为(2t+1,6),
∴抛物线C2的解析式为y=-(x-2t-1)2+6.
∵抛物线C1的顶点在抛物线C2上,
∴-(-1-2t-1)2+6=-2,
解得t1=3,t2=-5,
∴抛物线C2的解析式为y=-(x-7)2+6或y=-(x+9)2+6.
23.解:(1)证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∴∠AB1C=∠ACB.
又由旋转知∠ACB=∠A1CB1,
∴∠A1CB1=∠AB1C,∴BB1∥CA1.
(2)过点A作AD⊥BC于点D,如图所示.
∵AB=AC=5,AD⊥BC,BC=6,∴BD=CD=3.
在Rt△ABD中,AD==4,
∴△ABC的面积=BC·AD=×6×4=12.
过点C作CE⊥AB于点E,
∴CE==,∴BE==.
∵B1C=BC,CE⊥AB,∴B1E=BE=,
∴BB1=,∴AB1=,
∴△AB1C的面积=AB1·CE=.
24.解:(1)补全图形如图①所示.
图①
(2)连接AP′.∵将△ACP以点P为旋转中心,逆时针旋转60°,得到△P′BP,
∴∠APP′=60°,△ACP≌△P′BP,
∴∠CAP=∠BP′P,AP=P′P,AC=P′B=3,
∴△P′AP为等边三角形,
∴AP=AP′,∠PAP′=∠AP′P=60°.
∵∠CAB=30°,∴∠ACB+∠ABC=150°,
∴∠ABP′=360°-150°-60°-60°=90°.
在Rt△ABP′中,AP′==5,
∴AP=AP′=5.
(3)如图②所示,当∠CAB=120°时,AP的长有最大值,最大值是7.
图②
思路:
①由旋转可得∠ACP=∠P′BP,AP=P′P,AC=P′B;
②由∠CAB=120°,∠CPB=60°,可得∠ACP+∠ABP=180°,进而推出∠ABP+∠P′BP=180°,即A,B,P′三点共线;
③由AC=3,AB=4,可得AP=AP′=AB+P′B=7.
范围:旋转 时间:90分钟 分值:100分第Ⅰ卷 (选择题 共30分)
一、选择题(每小题3分,共30分)
1.风车应做成正面投影为中心对称图形,并且不是轴对称图形的样子,才能在风口处平稳旋转.如图,现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的黏合方法是( )
2.下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的是( )
3.在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B.(2,-3)
C.(-3,-2) D.(3,-2)
4.如图,△ABC是等边三角形,D是BC的中点,以点D为旋转中心,把△ABC顺时针旋转60°后所成的图形应是图中的( )
5.在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:①Y(a,b)=
(-a,b);②O(a,b)=(-a,-b);③X(a,b)=(a,-b).
按照以上变换有Y(O(1,2))=(1,-2),那么O(X(3,4))等于( )
A.(3,4) B.(3,-4)
C.(-3,4) D.(-3,-4)
6.对图的变化顺序描述正确的是( )
A.翻折、旋转、平移 B.翻折、平移、旋转
C.平移、翻折、旋转 D.旋转、翻折、平移
7.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5) B.(1,0)
C.(1,-1) D.(1.5,-0.5)
8.如图,已知在 ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的度数为( )
A.130° B.150°
C.160° D.170°
9.如图,在△ABC中,AC=6 ,∠A=45°,∠B=30°,P是BC边上一点,将PC绕着点P逆时针旋转得到PC′,旋转角为α(0°<α<180°),若旋转过程中,点C′始终落在△ABC内部(不包括边上),则PC长的取值范围是( )
A.0<PC<4 B.4<PC<6 C.0<PC<6 D.0<PC<4
10.一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如图下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形.例如图:若第一个正六边形下面标的数字为2,如图①,则先绕其中心顺时针旋转2格,再沿直线l翻折,得到第二个图形.若第一个正六边形下面标的数字为4,直线l的位置如图②所示,按照游戏规则,得到的第二个图形应是( )
第Ⅱ卷 (非选择题 共70分)
二、填空题(每小题3分,共18分)
11.如图,该图形可以看作是由一个“”每次旋转________得到的.
12.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是________.
13.已知点P(a+1,2a-3)关于原点的对称点在第二象限,则a的取值范围是______________.
14.如图,在平面直角坐标系中,四边形OABC与四边形CDEF都是正方形,OA=2,M,D分别是AB,BC的中点,当把正方形CDEF绕点C旋转某个角度或沿y轴上下平移后,若点F的对应点为F′,且OF′=OM,则点F′的坐标是__________________.
15.如图,菱形ABCD和菱形AEFG开始时互相重合,现将菱形AEFG绕点A顺时针旋转,设旋转角∠BAE=α(0°<α<360°),则当α=______________时,菱形AEFG的顶点F会落在菱形ABCD的对角线AC或BD所在的直线上.
16.如图是一个坐标方格盘,你可操纵一只遥控机器蛙在方格盘上进行跳步游戏,机器蛙每次跳步只能按如图下两种方式:第一种,向上、下、左、右可任意跳动1格或3格;第二种,跳到关于原点的对称点上.若机器蛙在点A(-5,4)处,现欲操纵它跳到点B(2,-3)处,则机器蛙至少要跳________次.
三、解答题(共52分)
17.(5分)如图①是利用正方形各边中点和弧的中点设计的正方形瓷砖图案,用四块如图①所示的正方形瓷砖拼成一个新的正方形图案,使拼成的图案既是轴对称图形,又是中心对称图形.请你在图②和图③中各画一种拼法(要求两种拼法不相同).
18.(5分)用直尺和圆规作图(不写作法,保留作图痕迹):
已知:如图,△A′B′C′是由△ABC以点O为中心经过一次旋转得到的,点A′,B′,C′分别是点A,B,C旋转后的对应点.
求作:旋转中心O.
19.(5分)如图,△DEF是由△ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说这些对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
20.(6分)如图,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接DC,已知∠DCB=30°.求证:DC2+BC2=AC2.
21.(7分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.
22.(7分)将抛物线C1:y=(x+1)2-2绕点P(t,2)旋转180°得到抛物线C2,若抛物线C1的顶点在抛物线C2上,同时抛物线C2的顶点在抛物线C1上,求抛物线C2的解析式.
23.(7分)在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针旋转,得到△A1B1C,且点B1在线段BA的延长线上(如图).
(1)求证:BB1∥CA1;
(2)求△AB1C的面积.
24.(10分)已知:在△ABC中,AB=4,AC=3,以CB为边作等边三角形CBP,连接AP,求AP的长.
这道题目难倒了小明,因为没有具体图形,发现△ABC不是一个固定的图形,也没有指定等边三角形CBP在BC所在直线的哪一侧,这两个不确定的因素会使得AP的长不一定是固定的,为此小明从特殊情况出发研究这个问题,按如图下步骤解决:
步骤1:取∠CAB=30°,以CB为边作等边三角形CBP,使点A与点P在BC所在直线的两侧;
步骤2:要想建立AB,AC,AP的联系,需要将这三条线段进行转移处理,由于图中有等边三角形,可以通过旋转来完成线段与角的转移,因此将△ACP以点P为旋转中心,逆时针旋转60°,得到△P′BP,通过推理与计算得到了此位置时AP的长.
(1)请结合小明的步骤在图中补全图形;
(2)结合(1)中补全后的图形求出此时AP的长;
(3)根据上述经验,改变∠CAB的度数,发现∠CAB在变化到某一角度时,AP的长有最大值,画出∠CAB为这个特殊角度时的示意图,写出AP长的最大值,并说明大致思路.
答案
1.A 可凭生活中的经验,也可以由风车的正面投影是中心对称图形,但不是轴对称图形进行判断.
2.A 选项B是轴对称图形,但不是中心对称图形;选项C是轴对称图形,但不是中心对称图形;选项D是中心对称图形,但不是轴对称图形;只有选项A既是中心对称图形,又是轴对称图形.
3.D 由题意可得,点P和点P′关于原点对称,它们的横、纵坐标分别互为相反数.
4.D
5.C 根据题意可得O(X(3,4))=O(3,-4)=(-3,4).故选C.
6.B
7.C 连接AA′,BB′,作BB′的垂直平分线,再作AA′的垂直平分线,两条直线相交于一点,此点即为旋转中心,坐标为(1,-1).
8.C 由四边形ABCD是平行四边形,
得AD∥BC.
又∵∠ADA′=50°,∴∠DA′E=130°.
易得∠E′A′B=∠EAB=30°,∴∠DA′E′=160°.
9.A 如图,过点C作CD⊥AB于点D,过点P作PH⊥AB于点H.
∵AC=6 ,∠A=45°,∠B=30°,
∴AD=CD=6,BC=2CD=12.
设PC=x=PC′,
则BP=12-x,PH=(12-x).
∵旋转过程中,点C′始终落在△ABC内部(不包括边上),∴PC′<PH,
即x<(12-x),解得x<4,即PC<4.
又∵PC>0,∴0<PC<4.
10.A 先绕其中心顺时针旋转4格:
再沿直线l翻折:
11.90° 12.3
13.-1<a< ∵点P关于原点的对称点在第二象限,∴点P在第四象限,
∴
解得∴-1<a<.
14.(0,)或(0,-)或(-1,2)或(1,2)
①若把正方形CDEF沿y轴上下平移,
∵OM==,
∴在y轴上点F有两个对应点,坐标分别为(0,),(0,-).
②若把正方形CDEF绕点C旋转某个角度,
连接OD,易证△OCD≌△OAM,∴OD=OM,则点D为点F的对应点,其坐标为(1,2);
在BC的延长线上点D关于y轴的对称点位置也存在一点F′,使OF′=OM,该点坐标为(-1,2).
15.60°或180°或300° 如图①,当点F在线段DB的延长线上时,∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC,∴∠AOF=90°.
∵AF=AC,∴OA=AF,
∴∠CAF=60°,即旋转角为60°;
如图②,当点F在线段CA的延长线上时,
∠CAF=180°,∴旋转角为180°;
如图③,当点F在线段BD的延长线上时,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC,
∴∠AOF=90°.
∵AF=AC,∴OA=AF,∴∠CAF=60°.
则旋转角为360°-60°=300°.
∴α=60°或180°或300°.
16.3 机器蛙在点A(-5,4)处,根据跳步游戏规则,可以先向右跳3格,再向下跳1格,然后跳到关于原点的对称点处,即可跳到点B(2,-3)处,故机器蛙至少要跳3次.
17.解:答案不唯一,如图:
18.解:如图所示:
19.解:(1)由图可知,点A(2,3),点D(-2,-3),点B(1,2),点E(-1,-2),点C(3,1),点F(-3,-1).
这些对应点的坐标特征:横、纵坐标分别互为相反数.
(2)由(1)可知a+3+2a=0,4-b+2b-3=0,解得a=-1,b=-1.
20.证明:连接EC.
∵将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,
∴△ABC≌△DBE,∴AC=DE,BC=BE.
又∵∠CBE=60°,∴△BCE是等边三角形,
∴EC=BC,∠BCE=60°.
又∵∠DCB=30°,∴∠DCE=90°,
∴DC2+EC2=DE2,∴DC2+BC2=AC2.
21.解:四边形ACFD是菱形.
理由:∵在Rt△ABC中,∠ACB=90°,∠B=30°,∴∠A=90°-∠B=60°,AC=AB.
∵将△ABC绕点C按顺时针方向旋转,得到△DEC,
∴AC=DC,AB=DE,∠ACB=∠DCE=90°,
∴△ACD是等边三角形,
∴AC=AD.
∵F是DE的中点,
∴DF=CF=DE,
∴AC=CF=DF=AD,∴四边形ACFD是菱形.
22.解:∵抛物线y=(x+1)2-2的顶点坐标为(-1,-2),
∴绕点P(t,2)旋转180°得到抛物线C2的顶点坐标为(2t+1,6),
∴抛物线C2的解析式为y=-(x-2t-1)2+6.
∵抛物线C1的顶点在抛物线C2上,
∴-(-1-2t-1)2+6=-2,
解得t1=3,t2=-5,
∴抛物线C2的解析式为y=-(x-7)2+6或y=-(x+9)2+6.
23.解:(1)证明:∵AB=AC,B1C=BC,
∴∠AB1C=∠B,∠B=∠ACB,
∴∠AB1C=∠ACB.
又由旋转知∠ACB=∠A1CB1,
∴∠A1CB1=∠AB1C,∴BB1∥CA1.
(2)过点A作AD⊥BC于点D,如图所示.
∵AB=AC=5,AD⊥BC,BC=6,∴BD=CD=3.
在Rt△ABD中,AD==4,
∴△ABC的面积=BC·AD=×6×4=12.
过点C作CE⊥AB于点E,
∴CE==,∴BE==.
∵B1C=BC,CE⊥AB,∴B1E=BE=,
∴BB1=,∴AB1=,
∴△AB1C的面积=AB1·CE=.
24.解:(1)补全图形如图①所示.
图①
(2)连接AP′.∵将△ACP以点P为旋转中心,逆时针旋转60°,得到△P′BP,
∴∠APP′=60°,△ACP≌△P′BP,
∴∠CAP=∠BP′P,AP=P′P,AC=P′B=3,
∴△P′AP为等边三角形,
∴AP=AP′,∠PAP′=∠AP′P=60°.
∵∠CAB=30°,∴∠ACB+∠ABC=150°,
∴∠ABP′=360°-150°-60°-60°=90°.
在Rt△ABP′中,AP′==5,
∴AP=AP′=5.
(3)如图②所示,当∠CAB=120°时,AP的长有最大值,最大值是7.
图②
思路:
①由旋转可得∠ACP=∠P′BP,AP=P′P,AC=P′B;
②由∠CAB=120°,∠CPB=60°,可得∠ACP+∠ABP=180°,进而推出∠ABP+∠P′BP=180°,即A,B,P′三点共线;
③由AC=3,AB=4,可得AP=AP′=AB+P′B=7.
同课章节目录
