湖南省邵阳市邵阳县2021-2022学年八年级下学期期末质量检测数学试题(word版 含答案)
文档属性
| 名称 | 湖南省邵阳市邵阳县2021-2022学年八年级下学期期末质量检测数学试题(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 242.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 00:00:00 | ||
图片预览


文档简介
2022年春季期末质量检测初中八年级试卷
数 学
时量120分钟 满分120分
一、选择题(本大题共10小题,每小题3分,共30分. 在每个小题给出的四个选项中,
只有一项符合题目要求,请将正确答案前的字母代号填入题后的括号内)
1. 在平面直角坐标系中,点M(m-1,2m)在y轴上,则点M的坐标是( )
A.(-1,0) B.(1,0) C.(0,2) D.(0,-2)
2. 下列四个图形中,是中心对称图形且不是轴对称图形的为( )
A. B. C. D.
3. 某商店准备一种包装袋来包装大米,经市场调查以后,绘制了如图(一)所示的频数直方图,请问选择最合适的包装为( )
A.3kg/包 B.4kg/包 C.5kg/包 D.6kg/包
4. 如图(二),在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,
AD=BE,则下列结论不一定成立的是( )
A.△ABE≌△BAD B.△ABE≌△CBE C.△AEF≌△BDF D.△ADC≌△BEC
5. 一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6. 函数中自变量的取值范围是( )
A. >-1 B. >1 C. D.
7. 正方形具有,而菱形不具有的性质是( )
A.四条边都相等 B. 对角线互相垂直
C.四个角都相等 D. 对角线互相平分
8. 如图(三),在△ABC中,∠ACB=90°,D为AB的中点,DE⊥AC于点E,下列结论中不一定成立的是( )
A.AE=CE B.BD=BC C.BC=2DE D.CD=AD
9. 如图(四),∠ABC=30°,点P是∠ABC的平分线上一点,点D是射线BC上一点,
∠DBP=∠DPB,PE⊥AB于点E,PF⊥BC于点F,PD=6,则PE的长为( )
A.6 B.5 C.4 D.3
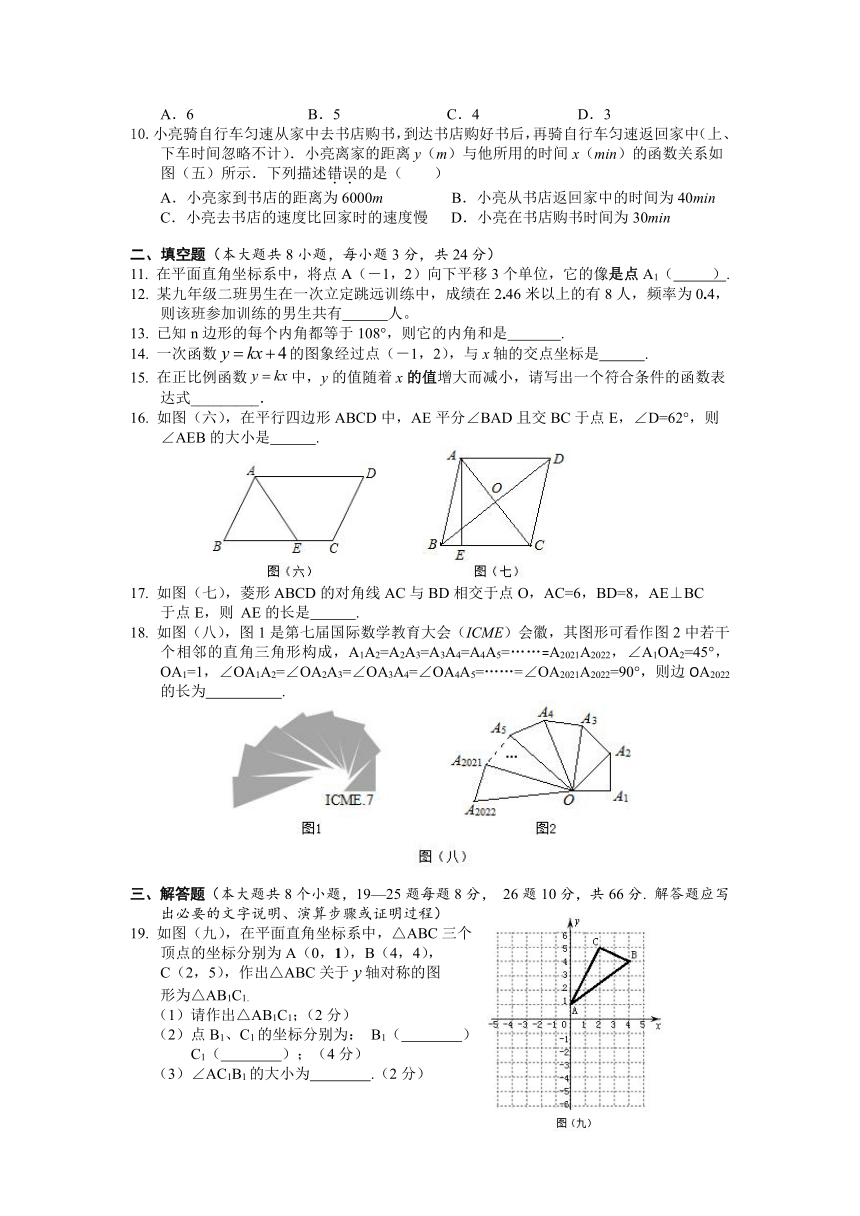
10.小亮骑自行车匀速从家中去书店购书,到达书店购好书后,再骑自行车匀速返回家中(上、下车时间忽略不计).小亮离家的距离y(m)与他所用的时间x(min)的函数关系如图(五)所示.下列描述错误的是( )
A.小亮家到书店的距离为6000m B.小亮从书店返回家中的时间为40min
C.小亮去书店的速度比回家时的速度慢 D.小亮在书店购书时间为30min
二、填空题(本大题共8小题,每小题3分,共24分)
11. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位,它的像是点A1( ).
12. 某九年级二班男生在一次立定跳远训练中,成绩在2.46米以上的有8人,频率为0.4,则该班参加训练的男生共有 人。
已知n边形的每个内角都等于108°,则它的内角和是 .
14. 一次函数的图象经过点(-1,2),与x轴的交点坐标是 .
15. 在正比例函数中,y的值随着x的值增大而减小,请写出一个符合条件的函数表达式_________.
16. 如图(六),在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=62°,则∠AEB的大小是 .
17. 如图(七),菱形ABCD的对角线AC与BD相交于点O,AC=6,BD=8,AE⊥BC
于点E,则 AE的长是 .
18. 如图(八),图1是第七届国际数学教育大会(ICME)会徽,其图形可看作图2中若干
个相邻的直角三角形构成,A1A2=A2A3=A3A4=A4A5=……=A2021A2022,∠A1OA2=45°,OA1=1,∠OA1A2=∠OA2A3=∠OA3A4=∠OA4A5=……=∠OA2021A2022=90°,则边OA2022的长为 .
三、解答题(本大题共8个小题,19—25题每题8分, 26题10分,共66分. 解答题应写出必要的文字说明、演算步骤或证明过程)
19. 如图(九),在平面直角坐标系中,△ABC三个
顶点的坐标分别为A(0,1),B(4,4),
C(2,5),作出△ABC关于轴对称的图
形为△AB1C1.
(1)请作出△AB1C1;(2分)
(2)点B1、C1的坐标分别为: B1( )、
C1( );(4分)
(3)∠AC1B1的大小为 .(2分)
20. 某学校为了提高师生节约用水的环保意识,及时关闭好水龙头,八年级一班学习小组的
同学合作对一个水龙头没有关紧时做漏水实验,他们用于接水的量筒最大容量为450
毫升,每隔1分钟观察量筒中水的数据如下表(精确到1毫升),并在图(十)的平面
直角坐标系中,描出了表格中每对数据对应的点.
时间 x(分钟) 1 2 3 4 5 6
漏出的水量 y(毫升) 15 30 45 60 75 90
请解答下列问题:
(1)观察图(十)中各点的分布规律,猜测这是什么
函数的图象,求出其表达式.(4分)
(2)按此漏水速度,多少分钟后量筒中的水开始溢出.
(2分)
(3)若按漏水速度漏水24小时,会流失水多少毫升?(2分)
21. 如图(十一),在△ABC中,∠C=90°,DE⊥AB于点E,AE=AC,∠B=50°,求∠DAC的大小.(8分)
22. 为进一步落实中小学生“作业、睡眠、手机、读物、体质”五项管理工作,某初中学校为
了解学生“睡眠”状况,数学社团成员采用随机抽样的方法,在全校学生中抽取了部分
学生,对他们一周内平均每天的睡眠时间(单位:)进行了调查,将数据整理后绘
制出频数分布表和频数直方图的一部分如下:
睡眠时间 频数 频率
7≤t<8 3 0.06
8≤t<9 10
9≤t<10 0.6
10≤t<11 7 0.14
请根据图表信息回答下列问题:
(1)在频数分布表中,_____,_____;(2分)
(2)将频数直方图补充完整;(2分)
(3)请估算该校1800名学生中睡眠不足9小时的人数;(2分)
(4)根据“睡眠”管理要求,初中生每天睡眠时间不低于9小时.请你根据以上调查
统计结果,向学校提出一条合理化的建议.(2分)
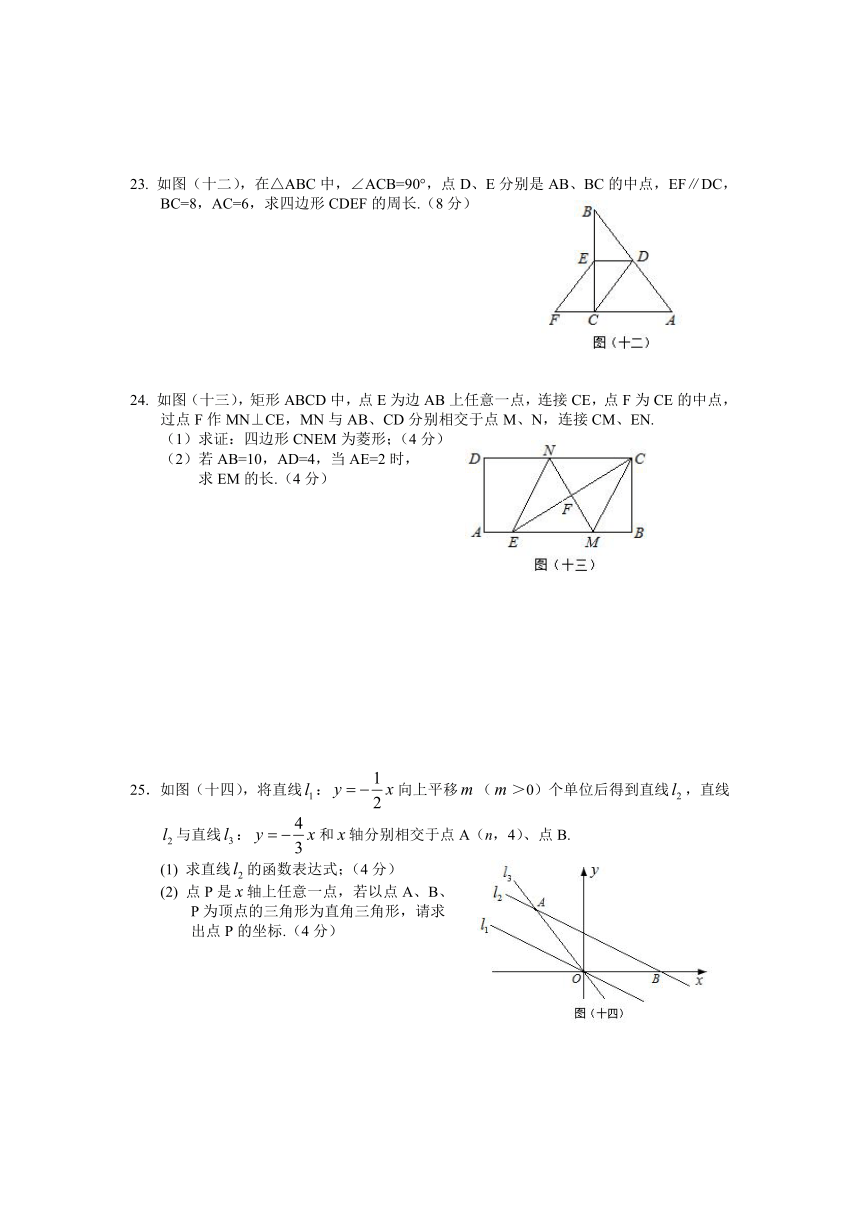
23. 如图(十二),在△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,EF∥DC,
BC=8,AC=6,求四边形CDEF的周长.(8分)
24. 如图(十三),矩形ABCD中,点E为边AB上任意一点,连接CE,点F为CE的中点,
过点F作MN⊥CE,MN与AB、CD分别相交于点M、N,连接CM、EN.
(1)求证:四边形CNEM为菱形;(4分)
(2)若AB=10,AD=4,当AE=2时,
求EM的长.(4分)
25.如图(十四),将直线:向上平移(>0)个单位后得到直线,直线与直线:和轴分别相交于点A(n,4)、点B.
(1) 求直线的函数表达式;(4分)
(2) 点P是轴上任意一点,若以点A、B、
P为顶点的三角形为直角三角形,请求
出点P的坐标.(4分)
26.对于湘教版数学八年级下册第73页例1:如图2-59,点E
是正方形ABCD的边AB上任意一点,过点D作DF⊥DE
交BC的延长线于点F. 求证:DE=DF.
小李在学习了该例题后,与学习小组的同学在“课后服务”
进一步开展了探究活动:
如图(十五),点E是正方形ABCD的边AB上任意一点,
点P在DE上,点M在边AD上,连接MP并延长与BC相交于点N.
(1)如图1,若MN⊥DE,则DE=MN仍然成立吗?请说
明理由.(4分)
(2)若AD=6,∠ADE=30°,点P是DE的中点.
① 如图2,若MN⊥DE,求PN的长;(4分)
② 如图3,当MN与DE不垂直时,是否存在这样的点
M使MN=DE?若存在,请直接写出DM的长;若不
存在,请说明理由.(2分)
2022年春季期末质量检测初中八年级试卷
数学参考答案及评分标准
一、选择题(本大题共有10个小题,每小题3分,共30分)
1—5小题 CDABA. 6—10小题BCBDC.
二. 填空题(本大题共有8个小题,每小题3分,共24分)
11.(—1,—1), 12. 20, 13. 540°, 14. (—2,0),
15.如(答案不唯一), 16. 59°, 17. , 18.
三、解答题(本大题共8个小题,19—25题每题8分, 26题10分,共66分. )
(
2
1
.
解:
∵
∠
C
=90°
,
∠B=
5
0°
,
∴
∠
BAC
=90°
—
∠B
=
90°
—
5
0°
=4
0°
.
…
2
分
∵
D
E⊥A
B
,
∠
C
=90°
,
∴
∠
ACD=
∠
AED=
90°
.
…
4
分
又
AD=AD
,
AC=AE
,
∴
△
ACD
≌△
AED
.
…
6
分
∴
∠
DAC=
∠
DAE=
∠
BAC=2
0°
.
…
8
分
) (
19.
解:(
1
)略
…
2
分
(
2
)
B
1
(
-
4
,
4
)
…
4
分
C
1
(
-2
,
5
)
…
6
分
(
3
)
90
°
…
8
分
)
(
20.解:(1)
正比例(或一次)函数的图象.
…
1
分
设
.
(
注:或设
)
将
x
=1
时,
y
=15
代入,得
.
∴
.
…
4
分
(
2
)当
时,
,∴
x
=30,
即30
分钟后量筒中的水开始溢出
.
…
6
分
(
3
)当
分钟时,
(毫升)
故会流失水
21600
毫升
.
…
8
分
)
(
23.
解:
∵
∠
ACB=
90°
,
BC=8
,
AC=6,
,
∴
=
.
…
1
分
又点
D
是
AB
的中点,
∴
.
…
2
分
∵
点
D
、
E
分别是
AB
、
BC
的中点,
∴E
D
∥
CA
,
.
…
3
分
又
E
D
∥CA
,
∴
四边形
CDEF
为平行四边形
.
…5
分
∴EF=DC=5
,
FC=ED=3.
…6
分
∴
四边形
CDEF
的周长为
2
(
CD+ED
)
=2×(5+3)=16.
…8
分
)
(
22.解:(1)a=
30
,
b=0.2.
…
2
分
(
2
)图略
.
…
4
分
(
3
)
.
…
6
分
(
4
)
建议学校尽量让学生在学校完成作业,课后少布置作业.
(
只要合理即可
)
.
…
8
分
)
(
24.
(
1)
证明:矩形
ABCD
中,
AB
∥
DC.
∴
∠
MEF=
∠
NCF
,
∠
EMF=
∠
CNF.
…
1
分
∵
点
F
为
CE
的中点,
∴
EF=CF
.
∴
△
EFM
≌△
C
F
N
,
∴
EM=CN.
…
2
分
∴四边形
CNEM
为平行四边形.
…
3
分
∵
MN
⊥
CE
于点
F
,
EF=CF
,
∴
NE=NC
,
四边形
CNEM
为菱形.
…
4
分
) (
24.
(
2)
解:在
菱形
CNEM
中,设
ME=MC=
x
,
又
AB=10
,
AE=2
,
∴
BM=10-2-
x
=8
-
x
.
…
5
分
矩形
ABCD
中,
∠
B
=90
°
,
BC=4.
∴
…
6
分
∴
.
∴
x
=5.
即
EM=5.
…
8
分
)
(
(求点
P
2
坐标的解法
2
:
过点
A
作
AP
2
⊥
AB
于交
x
轴于点
P
2
,则
∠
BAP
2
=
90°
.
设
P
2
P
1
=
x
,
AP
2
=
y
.
在直角三角形
AP
1
P
2
中,
∠
AP
1
P
2
=
90°
,
AP
1
=4
,
,
即
,
在直角三角形
BAP
2
中,
∠
BAP
2
=
90°
,
,
又
AB=
,
BP
2
=
x
+8.
即
,
由
、
式可解得
,
∴
OP
2
=OP
1
+
P
2
P
1
=3+2=5.
则
点
P
2
的坐标为
(-
5
,
0
)
.
)
注:参照评分
) (
25.
解:(
1
)依题意设
直线
的表达式为
.
∵
直线
:
经过
点
A
(
n
,
4
)
,
∴
,
,即点
A
(
-
3
,
4
)
.
…2分
将点
A
(
-
3
,
4
)的坐标代入
得
,解得
,
∴
.
…4分
(
2
)若以点
A
、
B
、
P
为顶点的三角形为直角三角形,
由题意可知
∠
ABP
为锐角,故只有
∠
APB
或
∠
BAP
可能为直角(即
AB
为斜边或直角边)
.
若
∠
APB
为直角,此时将点
P
设为点
P
1
.
过点
A
作
AP
1
⊥
x
轴于点
P
1
,则
∠
AP
1
B=
90°
.
由点
A
(
-
3
,
4
),得
OP
1
=3
,
故点
P
1
为(
-
3
,
0
)
.
…6分
若
∠
BAP
为直角,此时将点
P
设为点
P
2
.
过点
A
作
AP
2
⊥
AB
于交
x
轴于点
P
2
,则
∠
BAP
2
=
90°
.
在
中,令
,得
.
∴
点
B
为(
5
,
0
),即
OB=5.
又
,
∴
OA=OB
.
∴
∠
OAB=
∠
OBA.
∴
∠
OAP
2
=
90°
-
∠
OAB=
90°
-
∠
OBA=
∠
OP
2
A.
∴OP
2
=OA=5
,即点
P
2
(-
5
,
0
)
…8分
故点
P
的坐标为(
-
3
,
0
)或(
-5
,
0
)
.
)
(
26.(1)
DE=MN
仍然成立
.
…
1
分
证明:
如图
1
,
过点
M
作
MF
⊥
BC
于点
F.
由
正方形
ABCD
得,
∠
A=
∠
B=
90°
,
AB=A
D.
∴
四边形
ABFM
为矩形,
∴M
F
=AB=AD.
…
2
分
由
正方形
ABCD
得,
AB
∥
BC
,
∴
∠
DMP=
∠
FNM.
∵
MN
⊥
DE
,
∴
∠
DMP=
90°
—
∠
ADE
,
…
3
分
又
∠
AED=
90°
—
∠
ADE
,
∴
∠
AED=
∠
DMP=
∠
FNM.
又
∠
A=
∠
MFN=
90°
,
AD=MF.
∴
△D
A
E≌△
MFN.
∴
DE=MN.
…
4
分
(
方法
2
:
过点
D
作
DF
⊥
DE
于与
BC
的延长相交于点
F.
证明四边形
DMNF
为平行四边形,再利用
数学八年级下册第
73
页
例
1
的结论)
(
2
)
①
如图
2
,由
正方形
ABCD
得,
∠
A=
90°
.
∴
.
∵
∠
ADE
=
3
0
°,
∴DE=2AE.
又
AD=6
,
∴
,
∴
,
,
又
点
P
是
DE
的中点
,
∴
.
…
6
分
同理在直角
△
DMP
中
可求得,
MP=2.
(另解:连接
ME
,
∵
点
P
是
DE
的中点,
MN⊥DE
,
∴
ME=MD
,又
∠
MDE=3
0°
,
∴
∠
MED=
∠
MDE=3
0°
,
∠
AED=6
0°
.
∴
∠
AEM=
∠
PEM=3
0°
.
又
M
P
⊥DE
,
M
A
⊥
A
E
,
∴
MA=MP.
∴
AD=AM+MD=MP+MD=6
,
∵
∠
MDP=3
0°
,
∠
MPD=9
0°
,
∴
MD=2MP,
∴
3MP=6
,即
MP=2.)
∵
MN
⊥DE
,由(
1
)可得
.
∴
.
…
8
分
②
如图
3
,
当
MN
与
DE
不垂直时,存在这样的点
M
使
MN=DE
,
DM=2.
…
10
分
)
(
(
2
)中第
②
问的
解法
1
:
如图
3
—
1
,
过点
N
作
NH
⊥
AD
于点
H.
由
正方形
ABCD
得,
∠
A=
∠
B=
90°
.
∴
∠
A=
∠
B=
∠
AHN=
90°
.
∴
四边形
ABNH
为矩形
.
∴HN=AB=AD.
又
MN=DE
,
∴
△
HMN
≌△
A
ED
.
∴
∠
HMN=
∠
AED=
90°
—
∠
ADE=6
0°
.
过点
P
作
PK
⊥
AD
于点
K
,
∴
∠
MPK=
90°
—
∠
HMN=3
0°
.
∴MP=2MK.
由(
2
)中
①
可得
,
,
∵
∠
ADE
=
3
0
°
,
∴
.
∵
,
即
得
, MK=1.
∴
MD=KD
—
KM=3
—
1=2.
(
2
)中第
②
问的
解法
2
:
如图
3
—
2
,
过点
P
作
M
1
N
1
⊥
DE
分别交
AD
、
BC
于点
M
1
、
N
1.
由(
1
)可得,
M
1
N
1
=DE.
过点
P
作
HK
⊥
AD
分别交
AD
、
BC
于点
H
、
K.
再由点
P
是
DE
的中点,得出点
H
是
AD
的中点
.
则正方形
ABCD
关于直线
HK
对称
.
从而有,
M
1
N
1
关于
直线
HK
对称的像为
MN.
由(
2
)中的
①
可求得,
AM
1
=2
,
DM
1
=4.
∴
DM=AM
1
=2.
(
2
)中第
②
问的
解法
3
:
连接
AP
并延长交
CD
于点
F.
先证
AF=DE=MN
,再证
AF
⊥
MN.
从而转化为(
2
)中
①
的问题,求出
AM=4
,
DM=2.
)
数 学
时量120分钟 满分120分
一、选择题(本大题共10小题,每小题3分,共30分. 在每个小题给出的四个选项中,
只有一项符合题目要求,请将正确答案前的字母代号填入题后的括号内)
1. 在平面直角坐标系中,点M(m-1,2m)在y轴上,则点M的坐标是( )
A.(-1,0) B.(1,0) C.(0,2) D.(0,-2)
2. 下列四个图形中,是中心对称图形且不是轴对称图形的为( )
A. B. C. D.
3. 某商店准备一种包装袋来包装大米,经市场调查以后,绘制了如图(一)所示的频数直方图,请问选择最合适的包装为( )
A.3kg/包 B.4kg/包 C.5kg/包 D.6kg/包
4. 如图(二),在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,
AD=BE,则下列结论不一定成立的是( )
A.△ABE≌△BAD B.△ABE≌△CBE C.△AEF≌△BDF D.△ADC≌△BEC
5. 一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6. 函数中自变量的取值范围是( )
A. >-1 B. >1 C. D.
7. 正方形具有,而菱形不具有的性质是( )
A.四条边都相等 B. 对角线互相垂直
C.四个角都相等 D. 对角线互相平分
8. 如图(三),在△ABC中,∠ACB=90°,D为AB的中点,DE⊥AC于点E,下列结论中不一定成立的是( )
A.AE=CE B.BD=BC C.BC=2DE D.CD=AD
9. 如图(四),∠ABC=30°,点P是∠ABC的平分线上一点,点D是射线BC上一点,
∠DBP=∠DPB,PE⊥AB于点E,PF⊥BC于点F,PD=6,则PE的长为( )
A.6 B.5 C.4 D.3
10.小亮骑自行车匀速从家中去书店购书,到达书店购好书后,再骑自行车匀速返回家中(上、下车时间忽略不计).小亮离家的距离y(m)与他所用的时间x(min)的函数关系如图(五)所示.下列描述错误的是( )
A.小亮家到书店的距离为6000m B.小亮从书店返回家中的时间为40min
C.小亮去书店的速度比回家时的速度慢 D.小亮在书店购书时间为30min
二、填空题(本大题共8小题,每小题3分,共24分)
11. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位,它的像是点A1( ).
12. 某九年级二班男生在一次立定跳远训练中,成绩在2.46米以上的有8人,频率为0.4,则该班参加训练的男生共有 人。
已知n边形的每个内角都等于108°,则它的内角和是 .
14. 一次函数的图象经过点(-1,2),与x轴的交点坐标是 .
15. 在正比例函数中,y的值随着x的值增大而减小,请写出一个符合条件的函数表达式_________.
16. 如图(六),在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=62°,则∠AEB的大小是 .
17. 如图(七),菱形ABCD的对角线AC与BD相交于点O,AC=6,BD=8,AE⊥BC
于点E,则 AE的长是 .
18. 如图(八),图1是第七届国际数学教育大会(ICME)会徽,其图形可看作图2中若干
个相邻的直角三角形构成,A1A2=A2A3=A3A4=A4A5=……=A2021A2022,∠A1OA2=45°,OA1=1,∠OA1A2=∠OA2A3=∠OA3A4=∠OA4A5=……=∠OA2021A2022=90°,则边OA2022的长为 .
三、解答题(本大题共8个小题,19—25题每题8分, 26题10分,共66分. 解答题应写出必要的文字说明、演算步骤或证明过程)
19. 如图(九),在平面直角坐标系中,△ABC三个
顶点的坐标分别为A(0,1),B(4,4),
C(2,5),作出△ABC关于轴对称的图
形为△AB1C1.
(1)请作出△AB1C1;(2分)
(2)点B1、C1的坐标分别为: B1( )、
C1( );(4分)
(3)∠AC1B1的大小为 .(2分)
20. 某学校为了提高师生节约用水的环保意识,及时关闭好水龙头,八年级一班学习小组的
同学合作对一个水龙头没有关紧时做漏水实验,他们用于接水的量筒最大容量为450
毫升,每隔1分钟观察量筒中水的数据如下表(精确到1毫升),并在图(十)的平面
直角坐标系中,描出了表格中每对数据对应的点.
时间 x(分钟) 1 2 3 4 5 6
漏出的水量 y(毫升) 15 30 45 60 75 90
请解答下列问题:
(1)观察图(十)中各点的分布规律,猜测这是什么
函数的图象,求出其表达式.(4分)
(2)按此漏水速度,多少分钟后量筒中的水开始溢出.
(2分)
(3)若按漏水速度漏水24小时,会流失水多少毫升?(2分)
21. 如图(十一),在△ABC中,∠C=90°,DE⊥AB于点E,AE=AC,∠B=50°,求∠DAC的大小.(8分)
22. 为进一步落实中小学生“作业、睡眠、手机、读物、体质”五项管理工作,某初中学校为
了解学生“睡眠”状况,数学社团成员采用随机抽样的方法,在全校学生中抽取了部分
学生,对他们一周内平均每天的睡眠时间(单位:)进行了调查,将数据整理后绘
制出频数分布表和频数直方图的一部分如下:
睡眠时间 频数 频率
7≤t<8 3 0.06
8≤t<9 10
9≤t<10 0.6
10≤t<11 7 0.14
请根据图表信息回答下列问题:
(1)在频数分布表中,_____,_____;(2分)
(2)将频数直方图补充完整;(2分)
(3)请估算该校1800名学生中睡眠不足9小时的人数;(2分)
(4)根据“睡眠”管理要求,初中生每天睡眠时间不低于9小时.请你根据以上调查
统计结果,向学校提出一条合理化的建议.(2分)
23. 如图(十二),在△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,EF∥DC,
BC=8,AC=6,求四边形CDEF的周长.(8分)
24. 如图(十三),矩形ABCD中,点E为边AB上任意一点,连接CE,点F为CE的中点,
过点F作MN⊥CE,MN与AB、CD分别相交于点M、N,连接CM、EN.
(1)求证:四边形CNEM为菱形;(4分)
(2)若AB=10,AD=4,当AE=2时,
求EM的长.(4分)
25.如图(十四),将直线:向上平移(>0)个单位后得到直线,直线与直线:和轴分别相交于点A(n,4)、点B.
(1) 求直线的函数表达式;(4分)
(2) 点P是轴上任意一点,若以点A、B、
P为顶点的三角形为直角三角形,请求
出点P的坐标.(4分)
26.对于湘教版数学八年级下册第73页例1:如图2-59,点E
是正方形ABCD的边AB上任意一点,过点D作DF⊥DE
交BC的延长线于点F. 求证:DE=DF.
小李在学习了该例题后,与学习小组的同学在“课后服务”
进一步开展了探究活动:
如图(十五),点E是正方形ABCD的边AB上任意一点,
点P在DE上,点M在边AD上,连接MP并延长与BC相交于点N.
(1)如图1,若MN⊥DE,则DE=MN仍然成立吗?请说
明理由.(4分)
(2)若AD=6,∠ADE=30°,点P是DE的中点.
① 如图2,若MN⊥DE,求PN的长;(4分)
② 如图3,当MN与DE不垂直时,是否存在这样的点
M使MN=DE?若存在,请直接写出DM的长;若不
存在,请说明理由.(2分)
2022年春季期末质量检测初中八年级试卷
数学参考答案及评分标准
一、选择题(本大题共有10个小题,每小题3分,共30分)
1—5小题 CDABA. 6—10小题BCBDC.
二. 填空题(本大题共有8个小题,每小题3分,共24分)
11.(—1,—1), 12. 20, 13. 540°, 14. (—2,0),
15.如(答案不唯一), 16. 59°, 17. , 18.
三、解答题(本大题共8个小题,19—25题每题8分, 26题10分,共66分. )
(
2
1
.
解:
∵
∠
C
=90°
,
∠B=
5
0°
,
∴
∠
BAC
=90°
—
∠B
=
90°
—
5
0°
=4
0°
.
…
2
分
∵
D
E⊥A
B
,
∠
C
=90°
,
∴
∠
ACD=
∠
AED=
90°
.
…
4
分
又
AD=AD
,
AC=AE
,
∴
△
ACD
≌△
AED
.
…
6
分
∴
∠
DAC=
∠
DAE=
∠
BAC=2
0°
.
…
8
分
) (
19.
解:(
1
)略
…
2
分
(
2
)
B
1
(
-
4
,
4
)
…
4
分
C
1
(
-2
,
5
)
…
6
分
(
3
)
90
°
…
8
分
)
(
20.解:(1)
正比例(或一次)函数的图象.
…
1
分
设
.
(
注:或设
)
将
x
=1
时,
y
=15
代入,得
.
∴
.
…
4
分
(
2
)当
时,
,∴
x
=30,
即30
分钟后量筒中的水开始溢出
.
…
6
分
(
3
)当
分钟时,
(毫升)
故会流失水
21600
毫升
.
…
8
分
)
(
23.
解:
∵
∠
ACB=
90°
,
BC=8
,
AC=6,
,
∴
=
.
…
1
分
又点
D
是
AB
的中点,
∴
.
…
2
分
∵
点
D
、
E
分别是
AB
、
BC
的中点,
∴E
D
∥
CA
,
.
…
3
分
又
E
D
∥CA
,
∴
四边形
CDEF
为平行四边形
.
…5
分
∴EF=DC=5
,
FC=ED=3.
…6
分
∴
四边形
CDEF
的周长为
2
(
CD+ED
)
=2×(5+3)=16.
…8
分
)
(
22.解:(1)a=
30
,
b=0.2.
…
2
分
(
2
)图略
.
…
4
分
(
3
)
.
…
6
分
(
4
)
建议学校尽量让学生在学校完成作业,课后少布置作业.
(
只要合理即可
)
.
…
8
分
)
(
24.
(
1)
证明:矩形
ABCD
中,
AB
∥
DC.
∴
∠
MEF=
∠
NCF
,
∠
EMF=
∠
CNF.
…
1
分
∵
点
F
为
CE
的中点,
∴
EF=CF
.
∴
△
EFM
≌△
C
F
N
,
∴
EM=CN.
…
2
分
∴四边形
CNEM
为平行四边形.
…
3
分
∵
MN
⊥
CE
于点
F
,
EF=CF
,
∴
NE=NC
,
四边形
CNEM
为菱形.
…
4
分
) (
24.
(
2)
解:在
菱形
CNEM
中,设
ME=MC=
x
,
又
AB=10
,
AE=2
,
∴
BM=10-2-
x
=8
-
x
.
…
5
分
矩形
ABCD
中,
∠
B
=90
°
,
BC=4.
∴
…
6
分
∴
.
∴
x
=5.
即
EM=5.
…
8
分
)
(
(求点
P
2
坐标的解法
2
:
过点
A
作
AP
2
⊥
AB
于交
x
轴于点
P
2
,则
∠
BAP
2
=
90°
.
设
P
2
P
1
=
x
,
AP
2
=
y
.
在直角三角形
AP
1
P
2
中,
∠
AP
1
P
2
=
90°
,
AP
1
=4
,
,
即
,
在直角三角形
BAP
2
中,
∠
BAP
2
=
90°
,
,
又
AB=
,
BP
2
=
x
+8.
即
,
由
、
式可解得
,
∴
OP
2
=OP
1
+
P
2
P
1
=3+2=5.
则
点
P
2
的坐标为
(-
5
,
0
)
.
)
注:参照评分
) (
25.
解:(
1
)依题意设
直线
的表达式为
.
∵
直线
:
经过
点
A
(
n
,
4
)
,
∴
,
,即点
A
(
-
3
,
4
)
.
…2分
将点
A
(
-
3
,
4
)的坐标代入
得
,解得
,
∴
.
…4分
(
2
)若以点
A
、
B
、
P
为顶点的三角形为直角三角形,
由题意可知
∠
ABP
为锐角,故只有
∠
APB
或
∠
BAP
可能为直角(即
AB
为斜边或直角边)
.
若
∠
APB
为直角,此时将点
P
设为点
P
1
.
过点
A
作
AP
1
⊥
x
轴于点
P
1
,则
∠
AP
1
B=
90°
.
由点
A
(
-
3
,
4
),得
OP
1
=3
,
故点
P
1
为(
-
3
,
0
)
.
…6分
若
∠
BAP
为直角,此时将点
P
设为点
P
2
.
过点
A
作
AP
2
⊥
AB
于交
x
轴于点
P
2
,则
∠
BAP
2
=
90°
.
在
中,令
,得
.
∴
点
B
为(
5
,
0
),即
OB=5.
又
,
∴
OA=OB
.
∴
∠
OAB=
∠
OBA.
∴
∠
OAP
2
=
90°
-
∠
OAB=
90°
-
∠
OBA=
∠
OP
2
A.
∴OP
2
=OA=5
,即点
P
2
(-
5
,
0
)
…8分
故点
P
的坐标为(
-
3
,
0
)或(
-5
,
0
)
.
)
(
26.(1)
DE=MN
仍然成立
.
…
1
分
证明:
如图
1
,
过点
M
作
MF
⊥
BC
于点
F.
由
正方形
ABCD
得,
∠
A=
∠
B=
90°
,
AB=A
D.
∴
四边形
ABFM
为矩形,
∴M
F
=AB=AD.
…
2
分
由
正方形
ABCD
得,
AB
∥
BC
,
∴
∠
DMP=
∠
FNM.
∵
MN
⊥
DE
,
∴
∠
DMP=
90°
—
∠
ADE
,
…
3
分
又
∠
AED=
90°
—
∠
ADE
,
∴
∠
AED=
∠
DMP=
∠
FNM.
又
∠
A=
∠
MFN=
90°
,
AD=MF.
∴
△D
A
E≌△
MFN.
∴
DE=MN.
…
4
分
(
方法
2
:
过点
D
作
DF
⊥
DE
于与
BC
的延长相交于点
F.
证明四边形
DMNF
为平行四边形,再利用
数学八年级下册第
73
页
例
1
的结论)
(
2
)
①
如图
2
,由
正方形
ABCD
得,
∠
A=
90°
.
∴
.
∵
∠
ADE
=
3
0
°,
∴DE=2AE.
又
AD=6
,
∴
,
∴
,
,
又
点
P
是
DE
的中点
,
∴
.
…
6
分
同理在直角
△
DMP
中
可求得,
MP=2.
(另解:连接
ME
,
∵
点
P
是
DE
的中点,
MN⊥DE
,
∴
ME=MD
,又
∠
MDE=3
0°
,
∴
∠
MED=
∠
MDE=3
0°
,
∠
AED=6
0°
.
∴
∠
AEM=
∠
PEM=3
0°
.
又
M
P
⊥DE
,
M
A
⊥
A
E
,
∴
MA=MP.
∴
AD=AM+MD=MP+MD=6
,
∵
∠
MDP=3
0°
,
∠
MPD=9
0°
,
∴
MD=2MP,
∴
3MP=6
,即
MP=2.)
∵
MN
⊥DE
,由(
1
)可得
.
∴
.
…
8
分
②
如图
3
,
当
MN
与
DE
不垂直时,存在这样的点
M
使
MN=DE
,
DM=2.
…
10
分
)
(
(
2
)中第
②
问的
解法
1
:
如图
3
—
1
,
过点
N
作
NH
⊥
AD
于点
H.
由
正方形
ABCD
得,
∠
A=
∠
B=
90°
.
∴
∠
A=
∠
B=
∠
AHN=
90°
.
∴
四边形
ABNH
为矩形
.
∴HN=AB=AD.
又
MN=DE
,
∴
△
HMN
≌△
A
ED
.
∴
∠
HMN=
∠
AED=
90°
—
∠
ADE=6
0°
.
过点
P
作
PK
⊥
AD
于点
K
,
∴
∠
MPK=
90°
—
∠
HMN=3
0°
.
∴MP=2MK.
由(
2
)中
①
可得
,
,
∵
∠
ADE
=
3
0
°
,
∴
.
∵
,
即
得
, MK=1.
∴
MD=KD
—
KM=3
—
1=2.
(
2
)中第
②
问的
解法
2
:
如图
3
—
2
,
过点
P
作
M
1
N
1
⊥
DE
分别交
AD
、
BC
于点
M
1
、
N
1.
由(
1
)可得,
M
1
N
1
=DE.
过点
P
作
HK
⊥
AD
分别交
AD
、
BC
于点
H
、
K.
再由点
P
是
DE
的中点,得出点
H
是
AD
的中点
.
则正方形
ABCD
关于直线
HK
对称
.
从而有,
M
1
N
1
关于
直线
HK
对称的像为
MN.
由(
2
)中的
①
可求得,
AM
1
=2
,
DM
1
=4.
∴
DM=AM
1
=2.
(
2
)中第
②
问的
解法
3
:
连接
AP
并延长交
CD
于点
F.
先证
AF=DE=MN
,再证
AF
⊥
MN.
从而转化为(
2
)中
①
的问题,求出
AM=4
,
DM=2.
)
同课章节目录
