菱形及正方形性质及综合判定 学案(5课时)
文档属性
| 名称 | 菱形及正方形性质及综合判定 学案(5课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 141.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-08 21:57:21 | ||
图片预览

文档简介
第十一周/祥案第1课时19.2.2菱形判定(余全新)
学习目标:1.理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;
2.在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
学习重点:菱形的两个判定方法.
学习难点:判定方法的证明方法及运用.
一、知识目标:菱形判定方法 ①有 相等的 形是菱形
② 相等的 形是菱形.
③ 的 形是菱形
二目标训练
1、若四边形ABCD为平行四边形,请补充条件 使得四边形ABCD为菱形
2、 (1)对角线互相平分的四边形是 ; (2)对角线互相垂直平分的四边形是________;
(3)对角线相等且互相平分的四边形是________; (4)两组对边分别平行,且对角线 的四边形是菱形.
3、四边形ABCD中,AC与BD交于O ,根据下列条件判断四边形ABCD的形状
①AB∥CD,AD∥BC ; ②AB=CD,AD=BC ; ③AD∥BC 且AD=BC ;
④∠A=∠C,∠B=∠D ; ⑤OA=OC,OB=OD ; ⑥AB=AD且□ABCD ;
⑦AC=BD且□ABCD ; ⑧AC⊥BD且□ABCD ; ⑨∠A=∠C=∠B=∠D; ;
⑩∠A=90°且□ABCD ;
4、下列条件中,能判定四边形是菱形的是 ( ).
A两条对角线相等 B两条对角线互相垂直 C两条对角线相等且互相垂直 D两条对角线互相垂直平分
5、已知:如图所示,AD是△ABC的角平分线.DE∥AC交AB于E,DF∥AB交AC于F.四边形AEDF是菱形吗?说明你的理由.
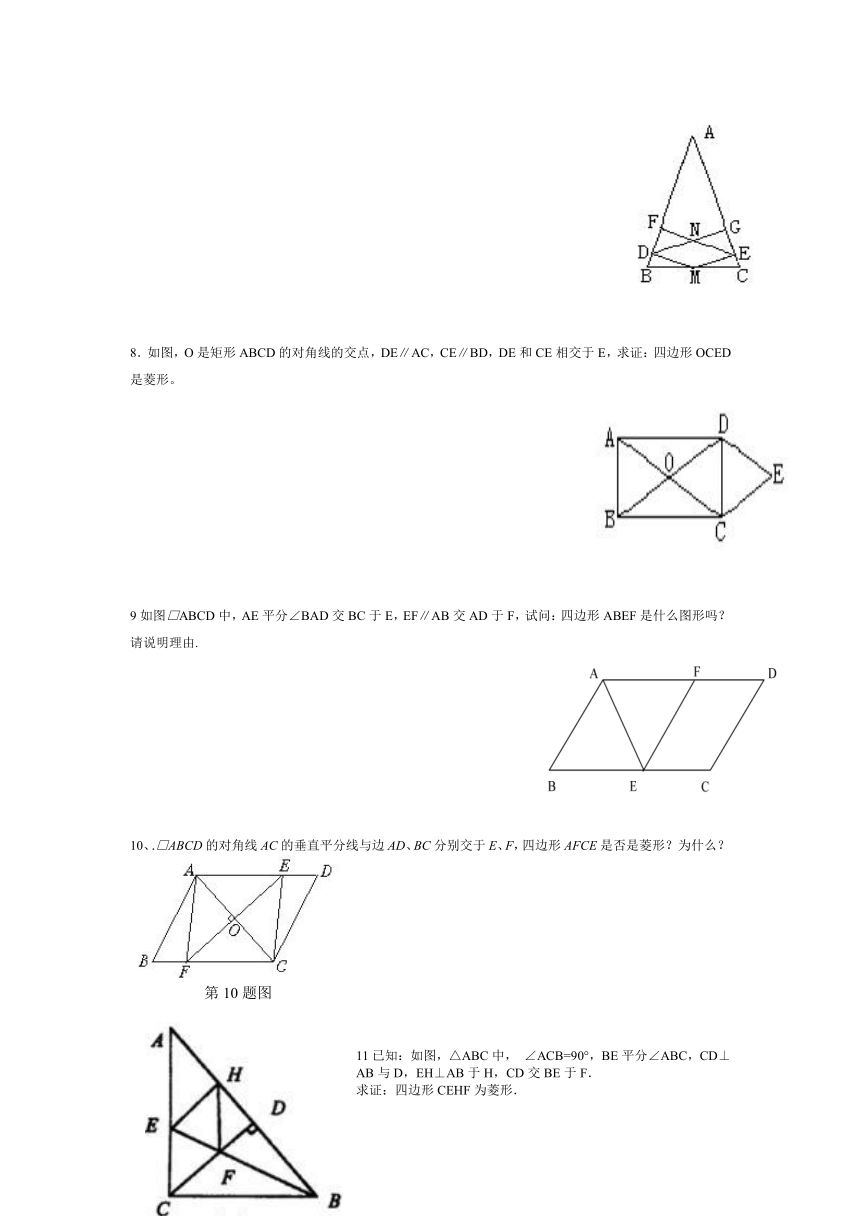
7、如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC.
求证:四边形MEND是菱形.
8.如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
9如图□ABCD中,AE平分∠BAD交BC于E,EF∥AB交AD于F,试问:四边形ABEF是什么图形吗?请说明理由.
10、.□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,四边形AFCE是否是菱形?为什么?
11已知:如图,△ABC中, ∠ACB=90°,BE平分∠ABC,CD⊥AB与D,EH⊥AB于H,CD交BE于F.
求证:四边形CEHF为菱形.
.
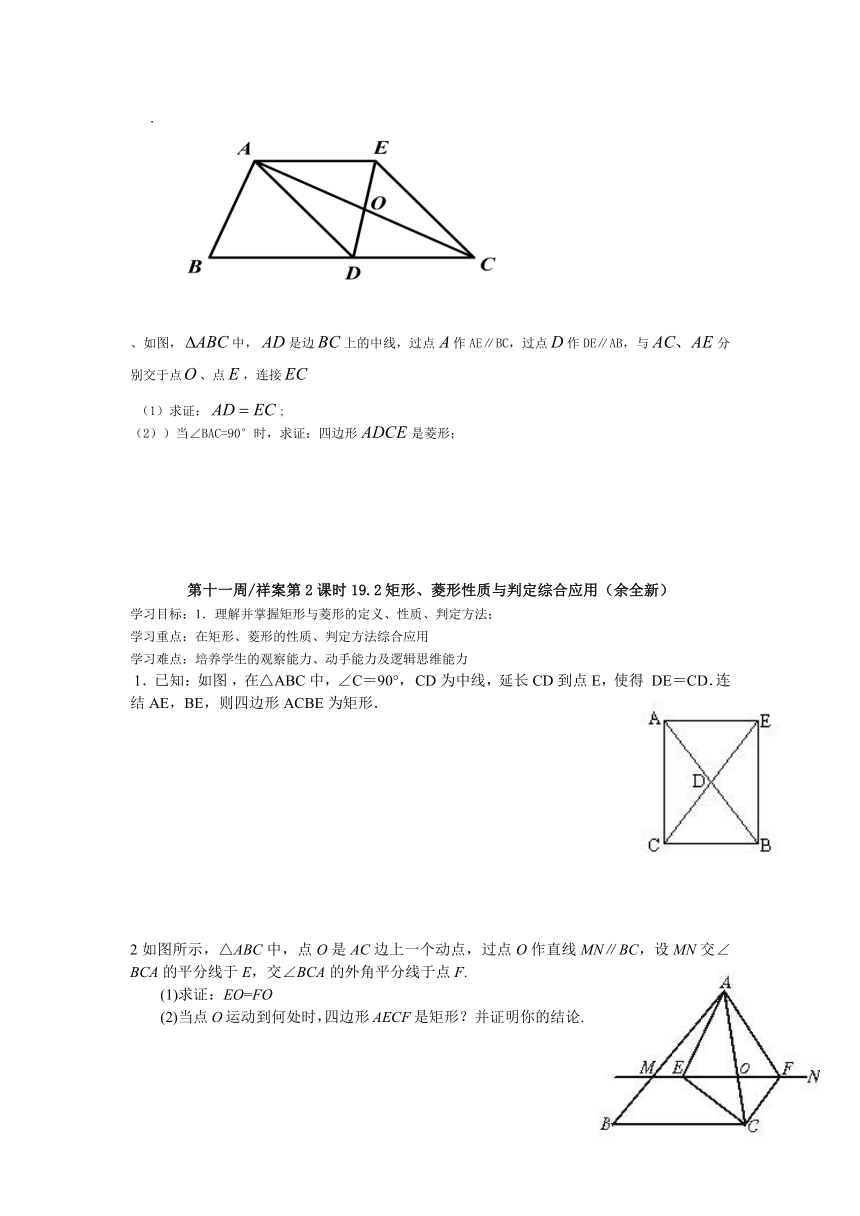
、如图,中,是边上的中线,过点作AE∥BC,过点作DE∥AB,与分别交于点、点,连接
(1)求证:;
(2))当∠BAC=90°时,求证:四边形是菱形;
第十一周/祥案第2课时19.2矩形、菱形性质与判定综合应用(余全新)
学习目标:1.理解并掌握矩形与菱形的定义、性质、判定方法;
学习重点:在矩形、菱形的性质、判定方法综合应用
学习难点:培养学生的观察能力、动手能力及逻辑思维能力
1.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.
2如图所示,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
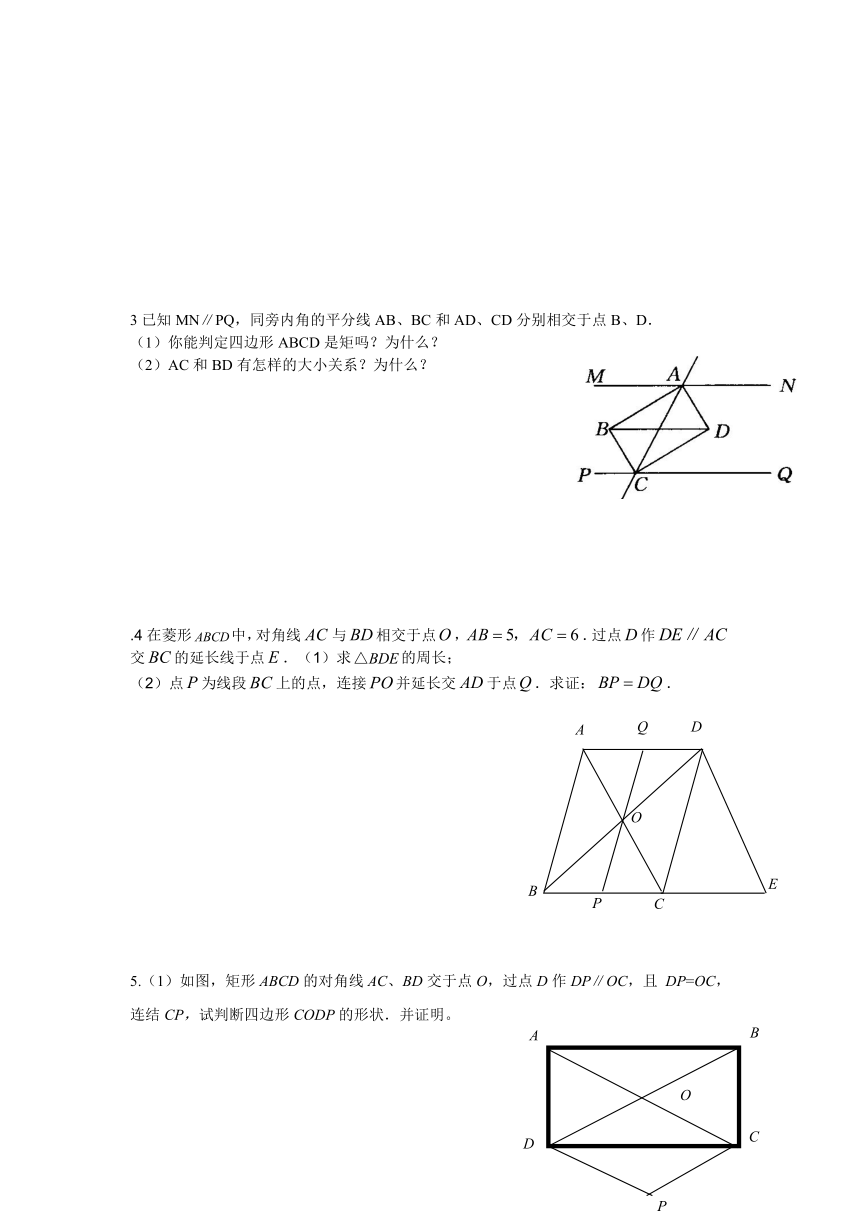
3已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)你能判定四边形ABCD是矩吗?为什么?
(2)AC和BD有怎样的大小关系?为什么?
.4在菱形中,对角线与相交于点,.过点作交的延长线于点.(1)求的周长;
(2)点为线段上的点,连接并延长交于点.求证:.
5.(1)如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.并证明。
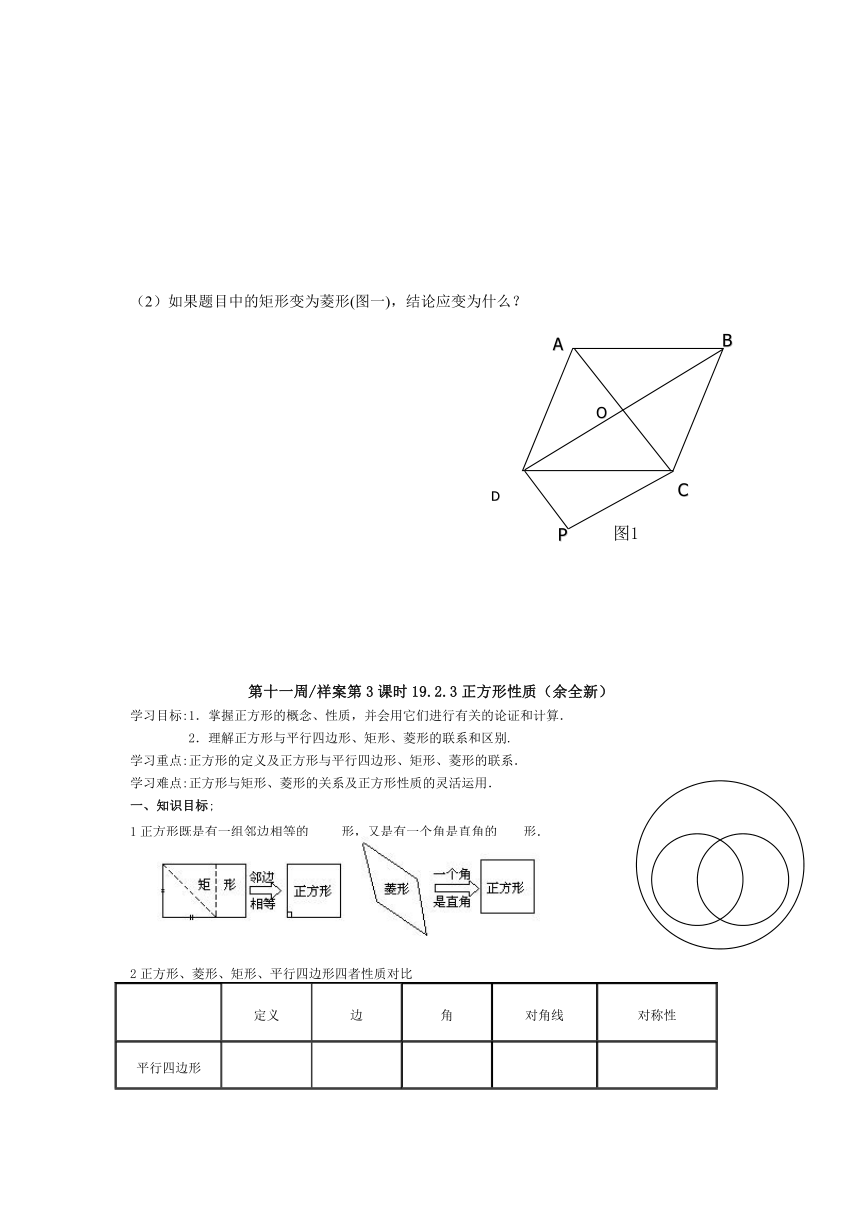
(2)如果题目中的矩形变为菱形(图一),结论应变为什么?
第十一周/祥案第3课时19.2.3正方形性质(余全新)
学习目标:1.掌握正方形的概念、性质,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别.
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质的灵活运用.
一、知识目标;
1正方形既是有一组邻边相等的 形,又是有一个角是直角的 形.
2正方形、菱形、矩形、平行四边形四者性质对比
定义 边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
3正方形、菱形、矩形、平行四边形四者之间的关系(在上右图填)
二、目标训练
1. 正方形的一条边长是3,那么它的对角线长是_______
2以正方形ABCD的边BC为边向外做等边△BCE,则∠AED的度数为
3如图,E为正方形ABCD内一点,且△EBC是等边三角形,则∠EAD= ,∠ECD= .
4.如图,正方形的边长为4cm,则图中阴影部分的面积为 cm2.
5.延长正方形ABCD的边AB到E,使BE=AC,则∠E= °
6.如图,依次连结一个边长为1的正方形各边的中点,得到第二个正方形,再依次连结第二个正方形各边的中点,得
到第三个正方形,按此方法继续下去, 则第六个正方形的面积是 .
7下列命题中的假命题是( ).
A.一组邻边相等的平行四边形是菱形 B.一组对边相等且有一个角是直角的四边形是矩形
C一组邻边相等的矩形是正方形 D.一组对边平行且相等的四边形是平行四边形
8四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
9 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,则△ABO的周长是( )
A.12+12 B.12+6 C.12+ D.24+6
10正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于( )
A B C D
10 把正方形绕着点,按顺时针方向旋转得到正方形,边与交于点(如图).试问线段与线段相等吗?请先观察猜想,然后再证明你的猜想.
11已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:EA⊥AF.
12如图所示,.四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
第十一周/祥案第4课时19.2.3正方形判定(余全新)
学习目标:1.理解并掌握正方形的判定方法;会用这些判定方法进行有关的论证;
2.在正方形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
学习重点:正方形的三个判定方法.
学习难点:判定方法的证明方法及运用.
一、知识目标:正方形判定方法 ①有 相等的 形是正方形
② 是直角的 形是正方形
③ 相等且有 是直角的 形是正方形.
二目标训练
1①已知四边形ABCD是菱形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
②已知四边形ABCD是矩形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
③已知四边形ABCD是平行四边形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
2下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( ) ②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( ) ④四条边都相等的四边形是正方形;( )
⑤四个角相等的四边形是正方形.( )
3在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F. ⑴求证::DE=DF
⑵只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明)
4已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形
5已知:△ABC中∠C=90°,∠BAC 与∠ABC 的平分线相交于点D,DE⊥AB于E,DF⊥BC于F.求证:四边形CEDF是正方形.
6已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
7正方形ABCD中,E、F、G、H且有AE=BF=CG=DH,(1)求证:四边形EFGH是正方形。
(2)若E、F、G、H为各边的四等分点且正方形ABCD面积是1求正方形EFGH的面积
8以△ABC的AB和AC为边向外分别作两个正方形ABDE和ACFG,M为BC的中点,
求证:(1)BG=CE (2)BG⊥CE
第十一周/祥案第5课时19.2特殊平行四边形之间的区别与联系(余全新)
学习目标:系统整理平行四边形、矩形、菱形和正方形之间的区别与联系。
学习重点:掌握平行四边形、矩形、菱形和正方形之间的区别和联系
学习难点:比较平行四边形、矩形、菱形和正方形之间的不同点
1〖从定义和从属关系上看〗
2〖从集合关系上看〗
3〖从性质上看〗
4〖从判定方法上看〗
5〖从对角线分得的三角形上看〗
6〖从四个内角的平分线所围成的四边形形状上看〗
7〖从顺次连结四边形各边中点所得的四边形(下称“中点四边形”)的形状上看〗
8〖从过四边形各顶点引对角线的平行线所围成的四边形的形状上看〗
9〖从四个外角的平分线围成的四边形形状上看〗------因卷面原因,同学们可以参照上6探究
第十一周/简案第6课时菱形性质及判定(余全新)
学习目标:系统整理菱形的性质及判定。
学习重点:应用菱形的性质及判定
学习难点:应用菱形的性质及判定
教学安排:评讲第十一周祥案第1、2课时
第十一周/简案第7课时正方形性质及判定(余全新)
学习目标:系统整理正方形的性质及判定。
学习重点:应用正方形的性质及判定
学习难点:应用正方形的性质及判定
教学安排:评讲第十一周祥案第3、4课时
第十一周/简案第8课时特殊平行四边形区别与联系(余全新)
学习目标:系统整理特殊平行四边形区别与联系
学习重点:掌握特殊平行四边形区别与联系
学习难点:理解特殊平行四边形区别与联系
教学安排:评讲第十一周祥案第6课时
第十一周/简案第9、10课时周考(余全新)
时间:2013年5月 日周四晚1、2节
一周教学反思
第5题图
第10题图
A
Q
D
E
B
P
C
O
A
B
D
C
O
P
图1
A
O
D
P
B
C
A
B
C
D
A
B
C
D
E
第6题图
A
B
F
C
D
E
O
D
C
A
B
G
H
F
E
第10题图
第12题图
2013年5月 日
学习目标:1.理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算;
2.在菱形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
学习重点:菱形的两个判定方法.
学习难点:判定方法的证明方法及运用.
一、知识目标:菱形判定方法 ①有 相等的 形是菱形
② 相等的 形是菱形.
③ 的 形是菱形
二目标训练
1、若四边形ABCD为平行四边形,请补充条件 使得四边形ABCD为菱形
2、 (1)对角线互相平分的四边形是 ; (2)对角线互相垂直平分的四边形是________;
(3)对角线相等且互相平分的四边形是________; (4)两组对边分别平行,且对角线 的四边形是菱形.
3、四边形ABCD中,AC与BD交于O ,根据下列条件判断四边形ABCD的形状
①AB∥CD,AD∥BC ; ②AB=CD,AD=BC ; ③AD∥BC 且AD=BC ;
④∠A=∠C,∠B=∠D ; ⑤OA=OC,OB=OD ; ⑥AB=AD且□ABCD ;
⑦AC=BD且□ABCD ; ⑧AC⊥BD且□ABCD ; ⑨∠A=∠C=∠B=∠D; ;
⑩∠A=90°且□ABCD ;
4、下列条件中,能判定四边形是菱形的是 ( ).
A两条对角线相等 B两条对角线互相垂直 C两条对角线相等且互相垂直 D两条对角线互相垂直平分
5、已知:如图所示,AD是△ABC的角平分线.DE∥AC交AB于E,DF∥AB交AC于F.四边形AEDF是菱形吗?说明你的理由.
7、如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC.
求证:四边形MEND是菱形.
8.如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
9如图□ABCD中,AE平分∠BAD交BC于E,EF∥AB交AD于F,试问:四边形ABEF是什么图形吗?请说明理由.
10、.□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,四边形AFCE是否是菱形?为什么?
11已知:如图,△ABC中, ∠ACB=90°,BE平分∠ABC,CD⊥AB与D,EH⊥AB于H,CD交BE于F.
求证:四边形CEHF为菱形.
.
、如图,中,是边上的中线,过点作AE∥BC,过点作DE∥AB,与分别交于点、点,连接
(1)求证:;
(2))当∠BAC=90°时,求证:四边形是菱形;
第十一周/祥案第2课时19.2矩形、菱形性质与判定综合应用(余全新)
学习目标:1.理解并掌握矩形与菱形的定义、性质、判定方法;
学习重点:在矩形、菱形的性质、判定方法综合应用
学习难点:培养学生的观察能力、动手能力及逻辑思维能力
1.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.
2如图所示,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
3已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)你能判定四边形ABCD是矩吗?为什么?
(2)AC和BD有怎样的大小关系?为什么?
.4在菱形中,对角线与相交于点,.过点作交的延长线于点.(1)求的周长;
(2)点为线段上的点,连接并延长交于点.求证:.
5.(1)如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且 DP=OC,连结CP,试判断四边形CODP的形状.并证明。
(2)如果题目中的矩形变为菱形(图一),结论应变为什么?
第十一周/祥案第3课时19.2.3正方形性质(余全新)
学习目标:1.掌握正方形的概念、性质,并会用它们进行有关的论证和计算.
2.理解正方形与平行四边形、矩形、菱形的联系和区别.
学习重点:正方形的定义及正方形与平行四边形、矩形、菱形的联系.
学习难点:正方形与矩形、菱形的关系及正方形性质的灵活运用.
一、知识目标;
1正方形既是有一组邻边相等的 形,又是有一个角是直角的 形.
2正方形、菱形、矩形、平行四边形四者性质对比
定义 边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
3正方形、菱形、矩形、平行四边形四者之间的关系(在上右图填)
二、目标训练
1. 正方形的一条边长是3,那么它的对角线长是_______
2以正方形ABCD的边BC为边向外做等边△BCE,则∠AED的度数为
3如图,E为正方形ABCD内一点,且△EBC是等边三角形,则∠EAD= ,∠ECD= .
4.如图,正方形的边长为4cm,则图中阴影部分的面积为 cm2.
5.延长正方形ABCD的边AB到E,使BE=AC,则∠E= °
6.如图,依次连结一个边长为1的正方形各边的中点,得到第二个正方形,再依次连结第二个正方形各边的中点,得
到第三个正方形,按此方法继续下去, 则第六个正方形的面积是 .
7下列命题中的假命题是( ).
A.一组邻边相等的平行四边形是菱形 B.一组对边相等且有一个角是直角的四边形是矩形
C一组邻边相等的矩形是正方形 D.一组对边平行且相等的四边形是平行四边形
8四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是( )
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
9 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,则△ABO的周长是( )
A.12+12 B.12+6 C.12+ D.24+6
10正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于( )
A B C D
10 把正方形绕着点,按顺时针方向旋转得到正方形,边与交于点(如图).试问线段与线段相等吗?请先观察猜想,然后再证明你的猜想.
11已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:EA⊥AF.
12如图所示,.四边形ABCD、DEFG都是正方形,连接AE、CG.
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
第十一周/祥案第4课时19.2.3正方形判定(余全新)
学习目标:1.理解并掌握正方形的判定方法;会用这些判定方法进行有关的论证;
2.在正方形的判定方法的探索与综合应用中,培养学生的观察能力、动手能力及逻辑思维能力.
学习重点:正方形的三个判定方法.
学习难点:判定方法的证明方法及运用.
一、知识目标:正方形判定方法 ①有 相等的 形是正方形
② 是直角的 形是正方形
③ 相等且有 是直角的 形是正方形.
二目标训练
1①已知四边形ABCD是菱形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
②已知四边形ABCD是矩形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
③已知四边形ABCD是平行四边形,当满足条件_________时,它成为正方形(填上你认为正确的一个条件即可).
2下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( ) ②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( ) ④四条边都相等的四边形是正方形;( )
⑤四个角相等的四边形是正方形.( )
3在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F. ⑴求证::DE=DF
⑵只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明)
4已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形
5已知:△ABC中∠C=90°,∠BAC 与∠ABC 的平分线相交于点D,DE⊥AB于E,DF⊥BC于F.求证:四边形CEDF是正方形.
6已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
7正方形ABCD中,E、F、G、H且有AE=BF=CG=DH,(1)求证:四边形EFGH是正方形。
(2)若E、F、G、H为各边的四等分点且正方形ABCD面积是1求正方形EFGH的面积
8以△ABC的AB和AC为边向外分别作两个正方形ABDE和ACFG,M为BC的中点,
求证:(1)BG=CE (2)BG⊥CE
第十一周/祥案第5课时19.2特殊平行四边形之间的区别与联系(余全新)
学习目标:系统整理平行四边形、矩形、菱形和正方形之间的区别与联系。
学习重点:掌握平行四边形、矩形、菱形和正方形之间的区别和联系
学习难点:比较平行四边形、矩形、菱形和正方形之间的不同点
1〖从定义和从属关系上看〗
2〖从集合关系上看〗
3〖从性质上看〗
4〖从判定方法上看〗
5〖从对角线分得的三角形上看〗
6〖从四个内角的平分线所围成的四边形形状上看〗
7〖从顺次连结四边形各边中点所得的四边形(下称“中点四边形”)的形状上看〗
8〖从过四边形各顶点引对角线的平行线所围成的四边形的形状上看〗
9〖从四个外角的平分线围成的四边形形状上看〗------因卷面原因,同学们可以参照上6探究
第十一周/简案第6课时菱形性质及判定(余全新)
学习目标:系统整理菱形的性质及判定。
学习重点:应用菱形的性质及判定
学习难点:应用菱形的性质及判定
教学安排:评讲第十一周祥案第1、2课时
第十一周/简案第7课时正方形性质及判定(余全新)
学习目标:系统整理正方形的性质及判定。
学习重点:应用正方形的性质及判定
学习难点:应用正方形的性质及判定
教学安排:评讲第十一周祥案第3、4课时
第十一周/简案第8课时特殊平行四边形区别与联系(余全新)
学习目标:系统整理特殊平行四边形区别与联系
学习重点:掌握特殊平行四边形区别与联系
学习难点:理解特殊平行四边形区别与联系
教学安排:评讲第十一周祥案第6课时
第十一周/简案第9、10课时周考(余全新)
时间:2013年5月 日周四晚1、2节
一周教学反思
第5题图
第10题图
A
Q
D
E
B
P
C
O
A
B
D
C
O
P
图1
A
O
D
P
B
C
A
B
C
D
A
B
C
D
E
第6题图
A
B
F
C
D
E
O
D
C
A
B
G
H
F
E
第10题图
第12题图
2013年5月 日
