19.2.1矩形性质及判定 学案
文档属性
| 名称 | 19.2.1矩形性质及判定 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 60.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-09 18:30:47 | ||
图片预览


文档简介
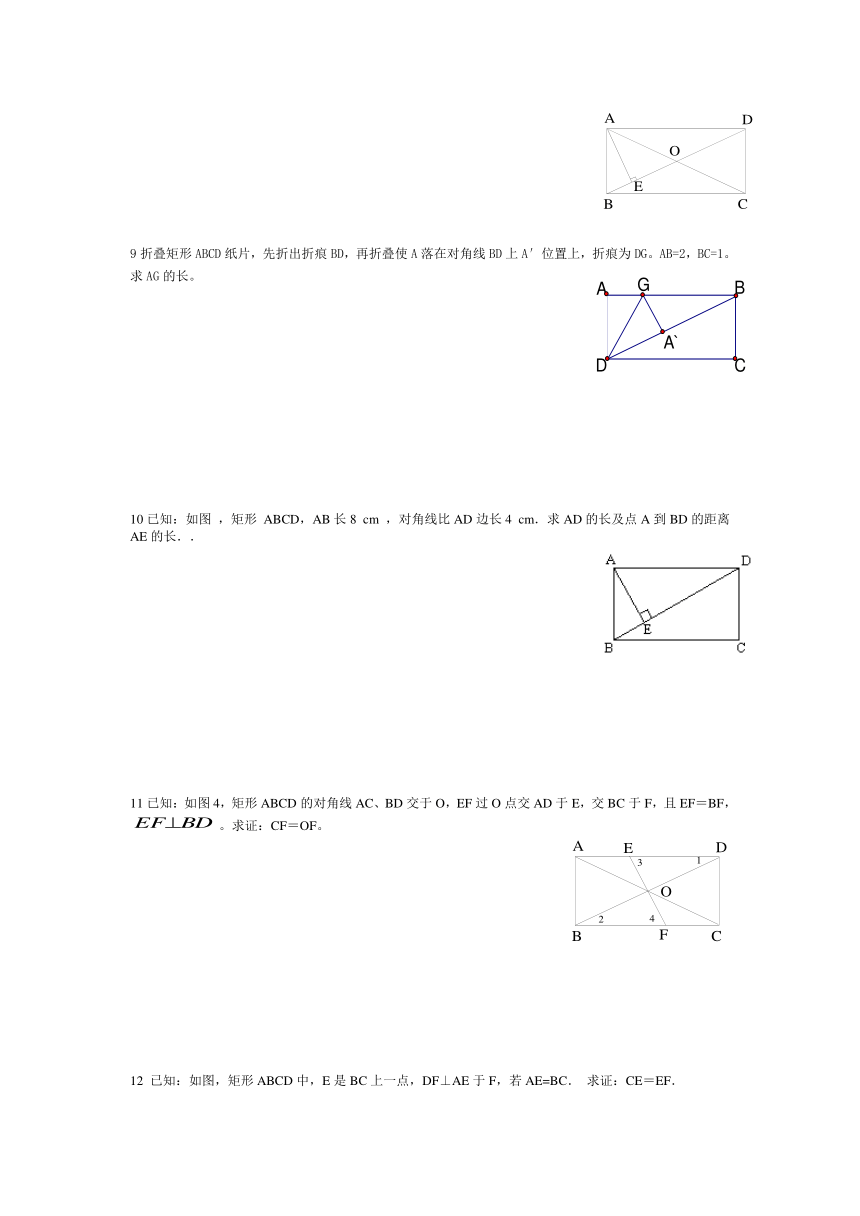
第十周/祥案第2课时19.2.1矩形性质1(余全新)
学习目标:掌握理解矩形的定义、性质及直角三角形斜边上中线的性质。
学习重点:掌握矩形的性质定理,会用定理进行有关的计算与证明。
学习难点:矩形的性质定理的应用
一、知识目标;
1、(1)在括号里填条件
(2)用语言表述两个箭头所表示的含意:①
②
2、矩形的性质:
名 称 平行四边形 矩形
性质 边
角
对角线
对称性
3、直角三角形斜边上的中线等于斜边的
(用几何语言表示):∵
∴
二、目标训练:
1已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
2已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
3矩形的两条对角线的夹角为60°,较短的边长为4.5厘米,则对角线长为 。
4已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
5已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,
则矩形的边长分别为 cm, cm, cm, cm.
6矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC, 若对角线 AC=6cm,
则周长= ,面积= 。
7. 在矩形ABCD中,,求这个矩形的周长。
8已知:如图3,矩形ABCD中,于E,且。求:的度数。
9折叠矩形ABCD纸片,先折出折痕BD,再折叠使A落在对角线BD上A′位置上,折痕为DG。AB=2,BC=1。求AG的长。
10已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长..
11已知:如图4,矩形ABCD的对角线AC、BD交于O,EF过O点交AD于E,交BC于F,且EF=BF,。求证:CF=OF。
12 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF.
第十周/祥案第3课时19.2.1矩形性质2(余全新)
学习目标:掌握理解矩形的定义、性质及直角三角形斜边上中线的性质。
学习重点:掌握矩形的性质定理,会用定理进行有关的计算与证明。
学习难点:矩形的性质定理的应用
1、由矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为1:3两部分,则该垂线与另一条对角线的夹角为( )A、22.5° B、45° C、30° D、60°
2矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
A12cm B10cm C7.5cm D5cm
3已知: O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,则∠AEO= .
A62.5° B、45° C、82.5° D、60°
4.在直角三角形ABC中,∠C=90°,AB=2AC,则∠B的度数是 .
A、22.5° B、45° C、30° D、60°
5.矩形ABCD中,AB=2BC,E在CD上且AB=AE,则∠CBE的度数等于 .
A、22.5° B、75° C、30° D、60°
6下列说法错误的是( ). A矩形的对角线互相平分 B矩形的对角线相等步为营
C有一个角是直角的四边形是矩形 D有一个角是直角的平行四边形叫做矩形
7矩形的对角线把矩形分成的三角形中全等三角形一共有( ).A2对 B4对 C6对 D8对
8如图,把矩形沿对折后使两部分重合,若,则=( )
A.110° B.115° C.120° D.130°
9在矩形中,平分,过点作于,延长交于点,下列结论中:;;;④,正确的是( )
A.②③ B.③④ C.①②④ D.②③④
10、在直角三角形ABC中,∠C=90°,CD是AB边上的中线,∠A=30°,AC=5 ,求△ADC的周长
11如图,将矩形ABCD沿对角线BD折叠,使点C落在F的位置,BF交AD于E,AD=8,AB=4,求△BED的面积。
12矩形ABCD中,AC与BD交于O点,于E,于F。
求证BE=CF。
13已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
14 如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.
求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
第十周/祥案第4课时19.2.1矩形判定(余全新)
学习目标:1.理解并掌握矩形的判定方法.
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习重点:矩形的判定.
学习难点:矩形的判定及性质的综合应用
一、知识目标
矩形判定方法 ①有 相等的 形是矩形
② 相等的 形是矩形.
③有 是直角的 形是矩形
二目标训练
1下列各句判定矩形的说法是否正确?为什么?
( )(1)有一个角是直角的四边形是矩形; ( )(2)有四个角是直角的四边形是矩形;
( )(3)四个角都相等的四边形是矩形; ( )(4)对角线相等的四边形是矩形;
( )(5)对角线相等且互相垂直的四边形是矩形; ( )(6)对角线互相平分且相等的四边形是矩形;
( )(7)对角线相等且有一个角是直角的四边形是矩形;
( )(8)一组邻边垂直一组对边平行且相等的四边形是矩形;
( )(9)两组对边分别平行,且对角线相等的四边形是矩形.
2下列说法正确的是( ).A有一组对角是直角的四边形一定是矩形
B有一组邻角是直角的四边形一定是矩形
C对角线互相平分的四边形是矩形 D对角互补的平行四边形是矩形
3工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;
4在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )A.测量对角线是否相互平分 B测量两组对边是否分别相等
C测量一组对角是否都为直角 D测量其中三角形是否都为直角
5能判断四边形是矩形的条件是( ) A、两条对角线互相平分 B、两条对角线相等
C、两条对角线互相平分且相等 D、两条对角线互相垂直。
6下列四边形中不是矩形的是( )
A、有三个角是直角的四边形是矩形 B、四个角都相等的四边形
C、一组对边平行且对角相等的四边形 D、对角线相等且互相平分的四边形
7如果E、F、G、H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是( )A、一组对边平行而另一组对边不平行B、对角线相等C、对角线互相垂直D、对角线相等互相平分
8、已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
9如图,EB=EC,EA=ED,AD=BC, ∠AEB=∠DEC,证明:四边形ABCD是矩形.
10如图所示,E为□ABCD外,AE⊥CE,BE⊥DE,求证:□ABCD为矩形
11、已知四边形ABCD中AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是矩形。
12如图,M、N分别是平行四边形ABCD对边AD、BC的中点,且AD=2AB,
求证,四边形PMQN是矩形。
( )
( )
A
D
B
C
B
A
D
C
O
D
A
B
C
O
E
F
H
E
D
C
B
A
F
第12题图
A
B
C
D
E
A
C
B
D
P
Q
第10题图
N
M
D
C
A
B
P
Q
学习目标:掌握理解矩形的定义、性质及直角三角形斜边上中线的性质。
学习重点:掌握矩形的性质定理,会用定理进行有关的计算与证明。
学习难点:矩形的性质定理的应用
一、知识目标;
1、(1)在括号里填条件
(2)用语言表述两个箭头所表示的含意:①
②
2、矩形的性质:
名 称 平行四边形 矩形
性质 边
角
对角线
对称性
3、直角三角形斜边上的中线等于斜边的
(用几何语言表示):∵
∴
二、目标训练:
1已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
2已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
3矩形的两条对角线的夹角为60°,较短的边长为4.5厘米,则对角线长为 。
4已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
5已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,
则矩形的边长分别为 cm, cm, cm, cm.
6矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC, 若对角线 AC=6cm,
则周长= ,面积= 。
7. 在矩形ABCD中,,求这个矩形的周长。
8已知:如图3,矩形ABCD中,于E,且。求:的度数。
9折叠矩形ABCD纸片,先折出折痕BD,再折叠使A落在对角线BD上A′位置上,折痕为DG。AB=2,BC=1。求AG的长。
10已知:如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长..
11已知:如图4,矩形ABCD的对角线AC、BD交于O,EF过O点交AD于E,交BC于F,且EF=BF,。求证:CF=OF。
12 已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF.
第十周/祥案第3课时19.2.1矩形性质2(余全新)
学习目标:掌握理解矩形的定义、性质及直角三角形斜边上中线的性质。
学习重点:掌握矩形的性质定理,会用定理进行有关的计算与证明。
学习难点:矩形的性质定理的应用
1、由矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为1:3两部分,则该垂线与另一条对角线的夹角为( )A、22.5° B、45° C、30° D、60°
2矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
A12cm B10cm C7.5cm D5cm
3已知: O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,则∠AEO= .
A62.5° B、45° C、82.5° D、60°
4.在直角三角形ABC中,∠C=90°,AB=2AC,则∠B的度数是 .
A、22.5° B、45° C、30° D、60°
5.矩形ABCD中,AB=2BC,E在CD上且AB=AE,则∠CBE的度数等于 .
A、22.5° B、75° C、30° D、60°
6下列说法错误的是( ). A矩形的对角线互相平分 B矩形的对角线相等步为营
C有一个角是直角的四边形是矩形 D有一个角是直角的平行四边形叫做矩形
7矩形的对角线把矩形分成的三角形中全等三角形一共有( ).A2对 B4对 C6对 D8对
8如图,把矩形沿对折后使两部分重合,若,则=( )
A.110° B.115° C.120° D.130°
9在矩形中,平分,过点作于,延长交于点,下列结论中:;;;④,正确的是( )
A.②③ B.③④ C.①②④ D.②③④
10、在直角三角形ABC中,∠C=90°,CD是AB边上的中线,∠A=30°,AC=5 ,求△ADC的周长
11如图,将矩形ABCD沿对角线BD折叠,使点C落在F的位置,BF交AD于E,AD=8,AB=4,求△BED的面积。
12矩形ABCD中,AC与BD交于O点,于E,于F。
求证BE=CF。
13已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
14 如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.
求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
第十周/祥案第4课时19.2.1矩形判定(余全新)
学习目标:1.理解并掌握矩形的判定方法.
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习重点:矩形的判定.
学习难点:矩形的判定及性质的综合应用
一、知识目标
矩形判定方法 ①有 相等的 形是矩形
② 相等的 形是矩形.
③有 是直角的 形是矩形
二目标训练
1下列各句判定矩形的说法是否正确?为什么?
( )(1)有一个角是直角的四边形是矩形; ( )(2)有四个角是直角的四边形是矩形;
( )(3)四个角都相等的四边形是矩形; ( )(4)对角线相等的四边形是矩形;
( )(5)对角线相等且互相垂直的四边形是矩形; ( )(6)对角线互相平分且相等的四边形是矩形;
( )(7)对角线相等且有一个角是直角的四边形是矩形;
( )(8)一组邻边垂直一组对边平行且相等的四边形是矩形;
( )(9)两组对边分别平行,且对角线相等的四边形是矩形.
2下列说法正确的是( ).A有一组对角是直角的四边形一定是矩形
B有一组邻角是直角的四边形一定是矩形
C对角线互相平分的四边形是矩形 D对角互补的平行四边形是矩形
3工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;
4在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )A.测量对角线是否相互平分 B测量两组对边是否分别相等
C测量一组对角是否都为直角 D测量其中三角形是否都为直角
5能判断四边形是矩形的条件是( ) A、两条对角线互相平分 B、两条对角线相等
C、两条对角线互相平分且相等 D、两条对角线互相垂直。
6下列四边形中不是矩形的是( )
A、有三个角是直角的四边形是矩形 B、四个角都相等的四边形
C、一组对边平行且对角相等的四边形 D、对角线相等且互相平分的四边形
7如果E、F、G、H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是( )A、一组对边平行而另一组对边不平行B、对角线相等C、对角线互相垂直D、对角线相等互相平分
8、已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
9如图,EB=EC,EA=ED,AD=BC, ∠AEB=∠DEC,证明:四边形ABCD是矩形.
10如图所示,E为□ABCD外,AE⊥CE,BE⊥DE,求证:□ABCD为矩形
11、已知四边形ABCD中AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是矩形。
12如图,M、N分别是平行四边形ABCD对边AD、BC的中点,且AD=2AB,
求证,四边形PMQN是矩形。
( )
( )
A
D
B
C
B
A
D
C
O
D
A
B
C
O
E
F
H
E
D
C
B
A
F
第12题图
A
B
C
D
E
A
C
B
D
P
Q
第10题图
N
M
D
C
A
B
P
Q
