19.2动点及特殊四边形
图片预览
文档简介
2013年春动点及特殊四边形
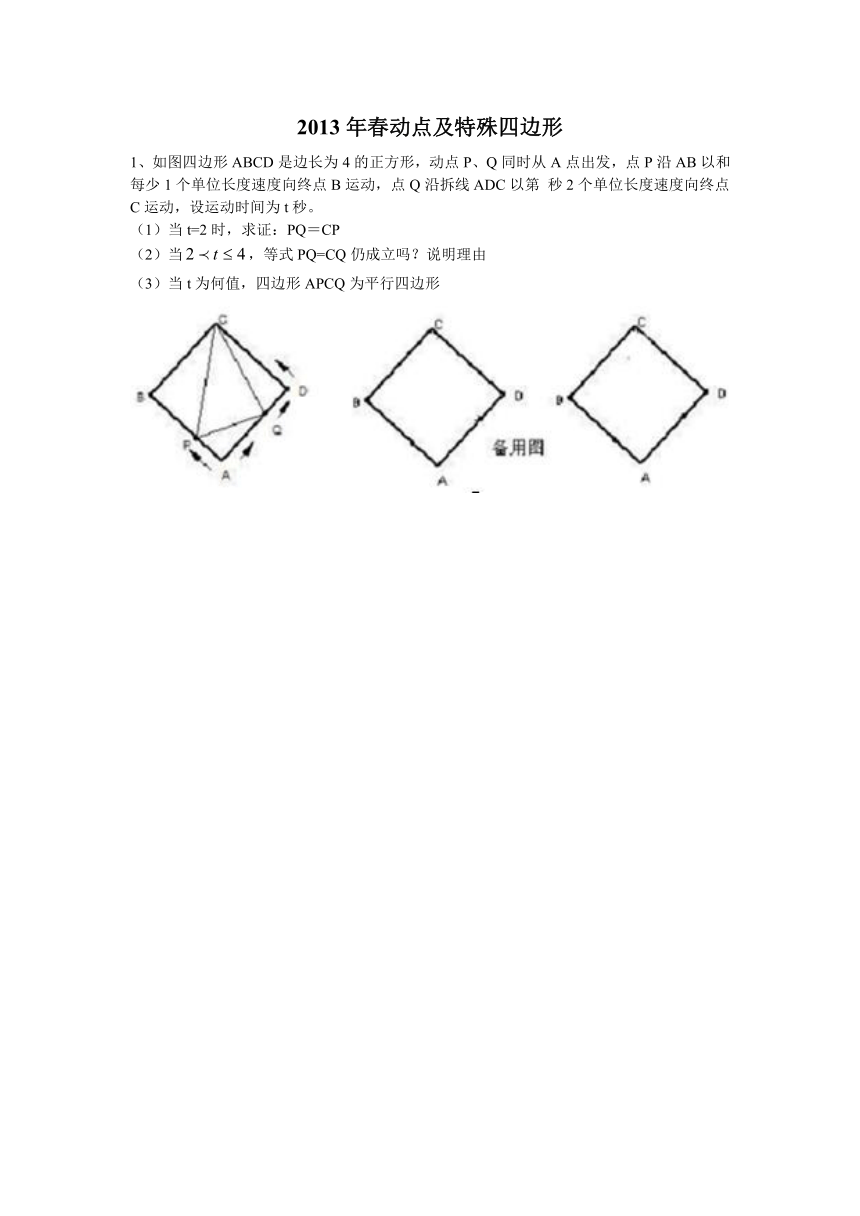
1、如图四边形ABCD是边长为4的正方形,动点P、Q同时从A点出发,点P沿AB以和每少1个单位长度速度向终点B运动,点Q沿拆线ADC以第 秒2个单位长度速度向终点C运动,设运动时间为t秒。
(1)当t=2时,求证:PQ=CP
(2)当,等式PQ=CQ仍成立吗?说明理由
(3)当t为何值,四边形APCQ为平行四边形
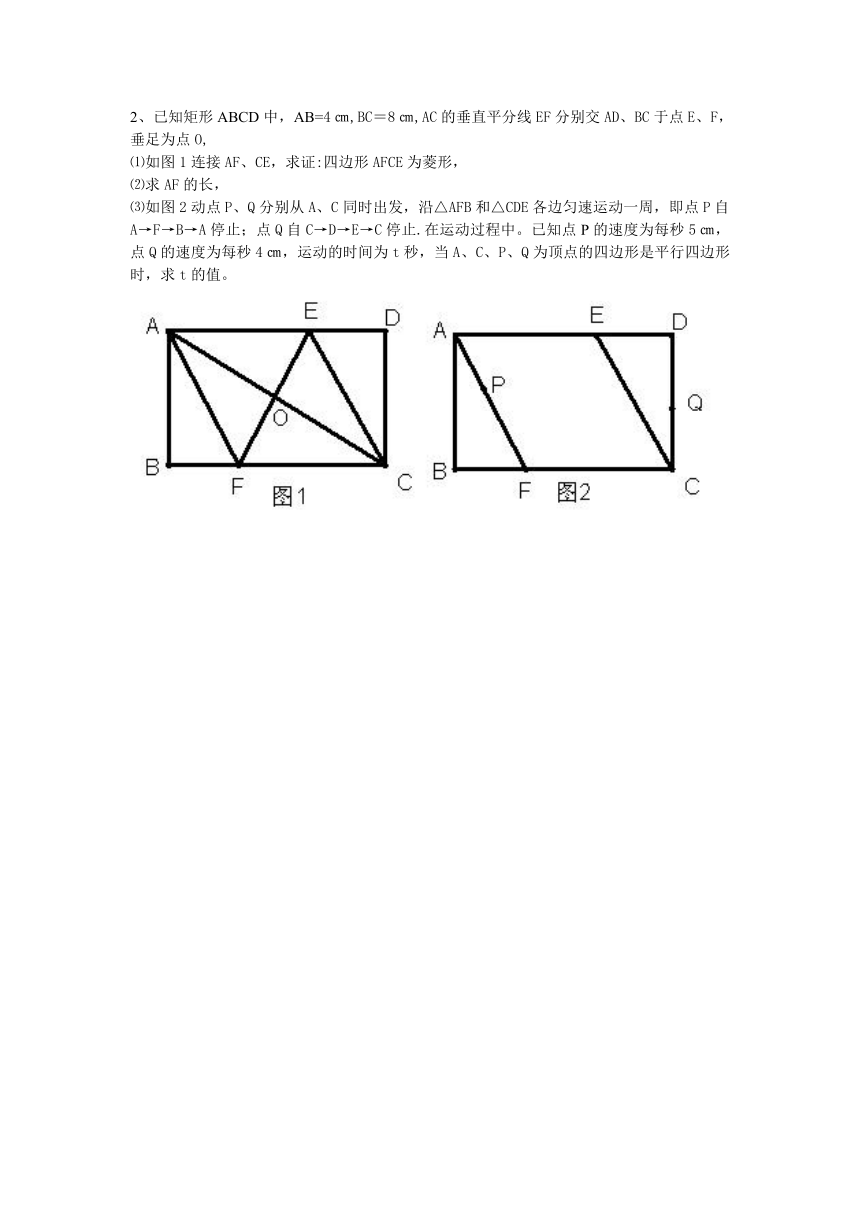
2、已知矩形ABCD中,AB=4㎝,BC=8㎝,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为点O,
⑴如图1连接AF、CE,求证:四边形AFCE为菱形,
⑵求AF的长,
⑶如图2动点P、Q分别从A、C同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止;点Q自C→D→E→C停止.在运动过程中。已知点P的速度为每秒5㎝,点Q的速度为每秒4㎝,运动的时间为t秒,当A、C、P、Q为顶点的四边形是平行四边形时,求t的值。
3、如图,已知ΔABC和ΔDEF是两个边长都为1cm的等边三角形,且B、D、C、E都在同一直线上,连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3cm,ΔABC沿着BE的方向以每秒1cm的速度运动,设ΔABC运动时间为t秒,
①当t为何值时,□ADFC是菱形?请说明你的理由;
②□ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
4、如图,已知中,厘米,厘米,点为的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
解:(1)①∵秒,
∴厘米,
∵厘米,点为的中点,
∴厘米.
又∵厘米,
∴厘米,
∴.
又∵,
∴,
∴.
②∵, ∴,
又∵,,
则,
∴点,点运动的时间秒,
∴厘米/秒.
(2)设经过秒后点与点第一次相遇,
由题意,得,
解得秒.
∴点共运动了厘米.∵,
∴点、点在边上相遇,
∴经过秒点与点第一次在边上相遇.
A
Q
C
D
B
P
A
Q
C
D
B
P
1、如图四边形ABCD是边长为4的正方形,动点P、Q同时从A点出发,点P沿AB以和每少1个单位长度速度向终点B运动,点Q沿拆线ADC以第 秒2个单位长度速度向终点C运动,设运动时间为t秒。
(1)当t=2时,求证:PQ=CP
(2)当,等式PQ=CQ仍成立吗?说明理由
(3)当t为何值,四边形APCQ为平行四边形
2、已知矩形ABCD中,AB=4㎝,BC=8㎝,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为点O,
⑴如图1连接AF、CE,求证:四边形AFCE为菱形,
⑵求AF的长,
⑶如图2动点P、Q分别从A、C同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止;点Q自C→D→E→C停止.在运动过程中。已知点P的速度为每秒5㎝,点Q的速度为每秒4㎝,运动的时间为t秒,当A、C、P、Q为顶点的四边形是平行四边形时,求t的值。
3、如图,已知ΔABC和ΔDEF是两个边长都为1cm的等边三角形,且B、D、C、E都在同一直线上,连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=0.3cm,ΔABC沿着BE的方向以每秒1cm的速度运动,设ΔABC运动时间为t秒,
①当t为何值时,□ADFC是菱形?请说明你的理由;
②□ADFC有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
4、如图,已知中,厘米,厘米,点为的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,与是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使与全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿三边运动,求经过多长时间点P与点Q第一次在的哪条边上相遇?
解:(1)①∵秒,
∴厘米,
∵厘米,点为的中点,
∴厘米.
又∵厘米,
∴厘米,
∴.
又∵,
∴,
∴.
②∵, ∴,
又∵,,
则,
∴点,点运动的时间秒,
∴厘米/秒.
(2)设经过秒后点与点第一次相遇,
由题意,得,
解得秒.
∴点共运动了厘米.∵,
∴点、点在边上相遇,
∴经过秒点与点第一次在边上相遇.
A
Q
C
D
B
P
A
Q
C
D
B
P
