3.1圆的认识
图片预览
文档简介
课题:圆的认识
备课时间: 备课人员:崔宗武、刘春梅、张跃震
学科: 数学 起草人: 张跃震
二次备课
研课人
一:题组练习
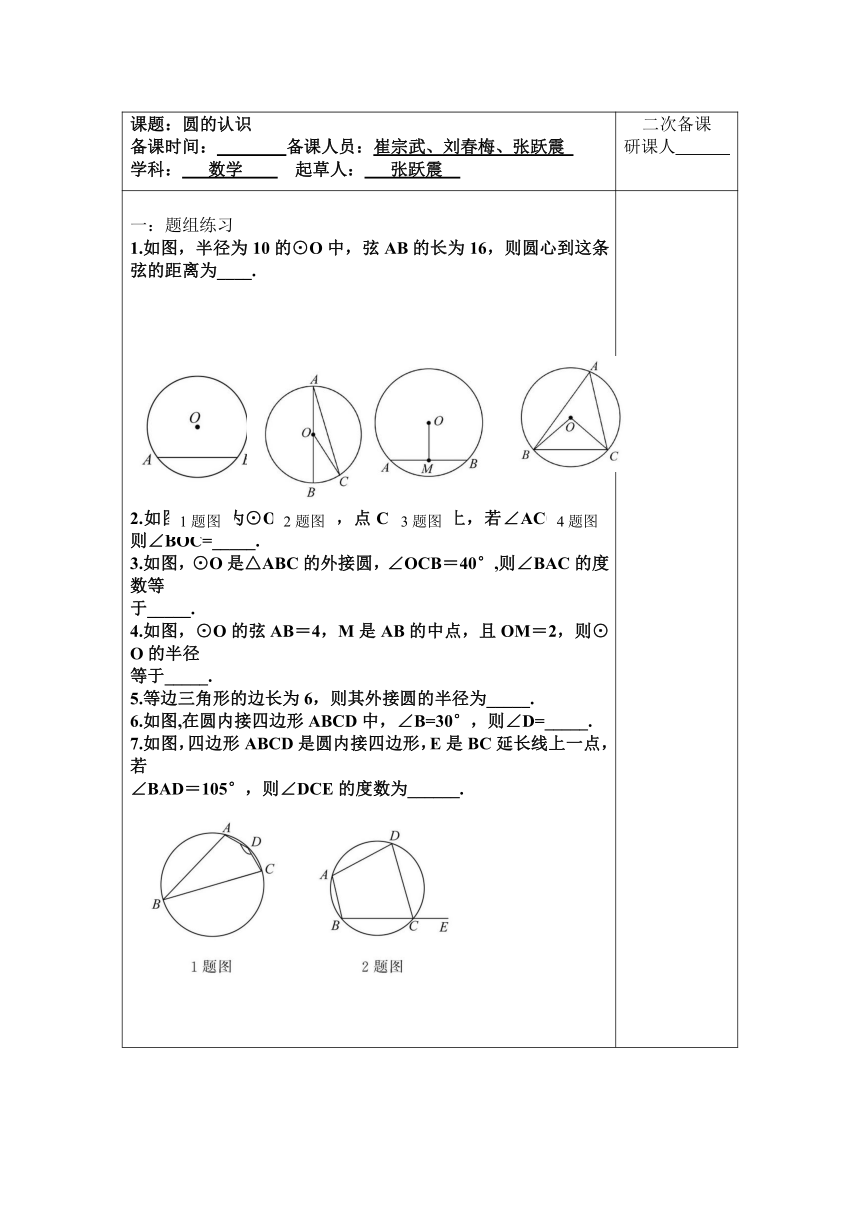
1.如图,半径为10的⊙O中,弦AB的长为16,则圆心到这条弦的距离为____.
2.如图,AB为⊙O的直径,点C在⊙O上,若∠ACO=16°,则∠BOC=_____.
3.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠BAC的度数等
于_____.
4.如图,⊙O的弦AB=4,M是AB的中点,且OM=2,则⊙O的半径
等于_____.
5.等边三角形的边长为6,则其外接圆的半径为_____.
6.如图,在圆内接四边形ABCD中,∠B=30°,则∠D=_____.
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若
∠BAD=105°,则∠DCE的度数为______.
知识点:
考点1、圆的对称性
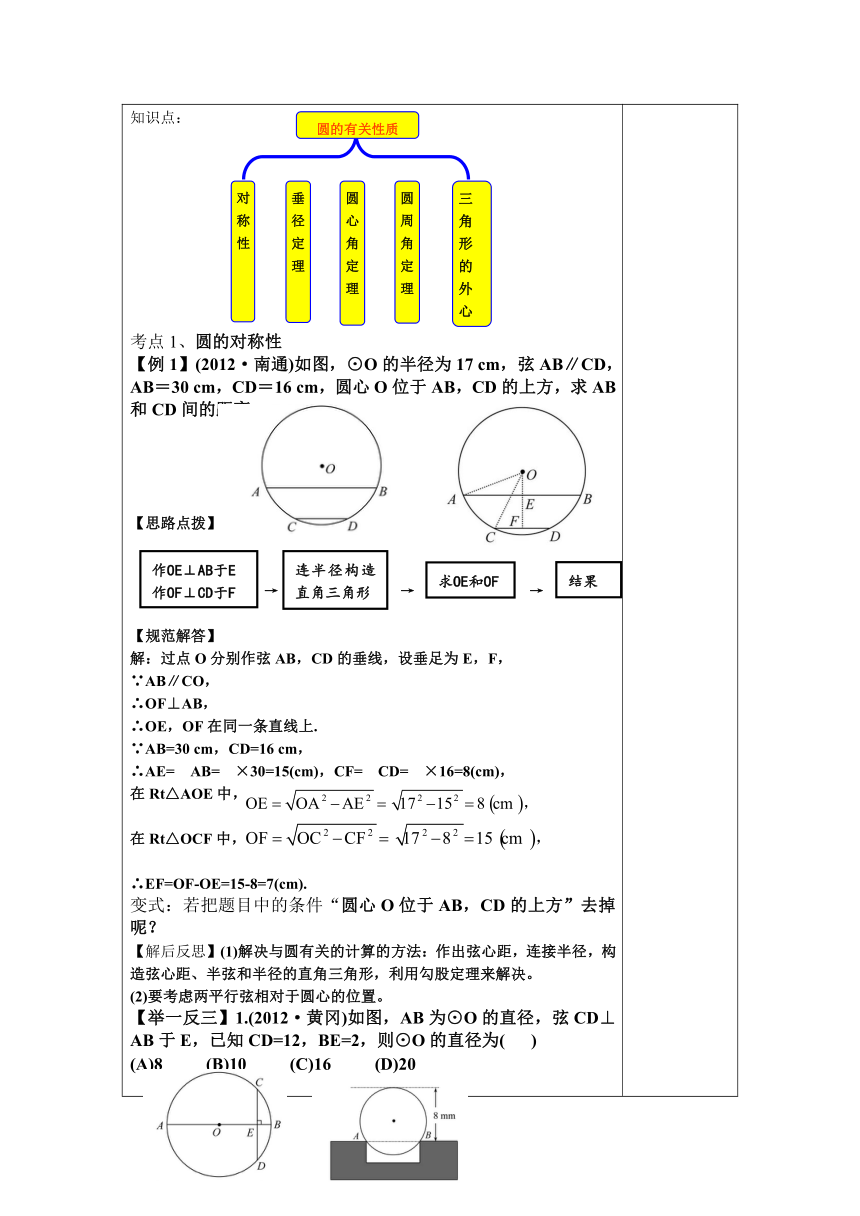
【例1】(2012·南通)如图,⊙O的半径为17 cm,弦AB∥CD,AB=30 cm,CD=16 cm,圆心O位于AB,CD的上方,求AB和CD间的距离.
【思路点拨】
→ → →
【规范解答】
解:过点O分别作弦AB,CD的垂线,设垂足为E,F,
∵AB∥CO,
∴OF⊥AB,
∴OE,OF在同一条直线上.
∵AB=30 cm,CD=16 cm,
∴AE= AB= ×30=15(cm),CF= CD= ×16=8(cm),
在Rt△AOE中,
在Rt△OCF中,
∴EF=OF-OE=15-8=7(cm).
变式:若把题目中的条件“圆心O位于AB,CD的上方”去掉呢?
【解后反思】(1)解决与圆有关的计算的方法:作出弦心距,连接半径,构造弦心距、半弦和半径的直角三角形,利用勾股定理来解决。
(2)要考虑两平行弦相对于圆心的位置。
【举一反三】1.(2012·黄冈)如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的直径为( )
(A)8 (B)10 (C)16 (D)20
2.(2012·衢州)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10 mm,测得钢珠顶端离零件表面的距离为8 mm,如图所示,则这个小圆孔的宽口AB的长度为_______mm.
圆周角与圆心角
考点二:圆周角与圆心角
【例2】(2011·凉山州中考)如图,∠AOB=100°,点C在⊙O上,且点C
不与A,B重合,则∠ACB的度数为( )
(A)50° (B)80°或50°(C)130° (D)50°或130°
【思路点拨】 →
→ →
解后反思:要考虑全面,分在优弧和劣弧上两种情况。
【举一反三】5.(2012·枣庄)如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则cos ∠OBC 的值为( )
(A) (B) (C) (D)
考点三:三角形的外接圆
【例3】(2011·内江中考)如图,⊙O是△ABC的外接圆,∠BAC=60°,
若⊙O的半径OC为2,则弦BC的长为( )
(A)1 (B)
(C)2 (D)2
解后反思:正确理解三角形外接圆的概念,
并与三角形内切圆的圆心的区别。
【举一反三】9.(2011·玉林中考)小英家的圆形镜子被打碎了,她拿了如图
(网格中的每个小正方形边长为1)所示的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
(A)2 (B) (C)2 (D)3
教学设计理念
研课交流反思
从这节课得到启示;一、具有良好的课堂学习氛围。二、学习内容是否符合课程标准的要求。三、课堂教学设计是否满足学生发展和有的效学习。四、加强转变学生的学习方式,使学生达到自主合作学习。五、教学中渗透态度情感培养。六、让反思成为习惯,让反思促进教学成长。
一节好课永远是有条件的,所以好课也是相对的。如同我们自己上一堂非常满意的课,但反思下来总有遗憾,总有可圈可点之处。即使运用同一教学评价标准,针对不同的地区,不同的课堂,不同的教师,评价结果还是会有差异的。总之,为了促进教师的提高和发展,是为鼓励教师完善自己的课堂。
备课时间: 备课人员:崔宗武、刘春梅、张跃震
学科: 数学 起草人: 张跃震
二次备课
研课人
一:题组练习
1.如图,半径为10的⊙O中,弦AB的长为16,则圆心到这条弦的距离为____.
2.如图,AB为⊙O的直径,点C在⊙O上,若∠ACO=16°,则∠BOC=_____.
3.如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠BAC的度数等
于_____.
4.如图,⊙O的弦AB=4,M是AB的中点,且OM=2,则⊙O的半径
等于_____.
5.等边三角形的边长为6,则其外接圆的半径为_____.
6.如图,在圆内接四边形ABCD中,∠B=30°,则∠D=_____.
7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若
∠BAD=105°,则∠DCE的度数为______.
知识点:
考点1、圆的对称性
【例1】(2012·南通)如图,⊙O的半径为17 cm,弦AB∥CD,AB=30 cm,CD=16 cm,圆心O位于AB,CD的上方,求AB和CD间的距离.
【思路点拨】
→ → →
【规范解答】
解:过点O分别作弦AB,CD的垂线,设垂足为E,F,
∵AB∥CO,
∴OF⊥AB,
∴OE,OF在同一条直线上.
∵AB=30 cm,CD=16 cm,
∴AE= AB= ×30=15(cm),CF= CD= ×16=8(cm),
在Rt△AOE中,
在Rt△OCF中,
∴EF=OF-OE=15-8=7(cm).
变式:若把题目中的条件“圆心O位于AB,CD的上方”去掉呢?
【解后反思】(1)解决与圆有关的计算的方法:作出弦心距,连接半径,构造弦心距、半弦和半径的直角三角形,利用勾股定理来解决。
(2)要考虑两平行弦相对于圆心的位置。
【举一反三】1.(2012·黄冈)如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的直径为( )
(A)8 (B)10 (C)16 (D)20
2.(2012·衢州)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10 mm,测得钢珠顶端离零件表面的距离为8 mm,如图所示,则这个小圆孔的宽口AB的长度为_______mm.
圆周角与圆心角
考点二:圆周角与圆心角
【例2】(2011·凉山州中考)如图,∠AOB=100°,点C在⊙O上,且点C
不与A,B重合,则∠ACB的度数为( )
(A)50° (B)80°或50°(C)130° (D)50°或130°
【思路点拨】 →
→ →
解后反思:要考虑全面,分在优弧和劣弧上两种情况。
【举一反三】5.(2012·枣庄)如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则cos ∠OBC 的值为( )
(A) (B) (C) (D)
考点三:三角形的外接圆
【例3】(2011·内江中考)如图,⊙O是△ABC的外接圆,∠BAC=60°,
若⊙O的半径OC为2,则弦BC的长为( )
(A)1 (B)
(C)2 (D)2
解后反思:正确理解三角形外接圆的概念,
并与三角形内切圆的圆心的区别。
【举一反三】9.(2011·玉林中考)小英家的圆形镜子被打碎了,她拿了如图
(网格中的每个小正方形边长为1)所示的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( )
(A)2 (B) (C)2 (D)3
教学设计理念
研课交流反思
从这节课得到启示;一、具有良好的课堂学习氛围。二、学习内容是否符合课程标准的要求。三、课堂教学设计是否满足学生发展和有的效学习。四、加强转变学生的学习方式,使学生达到自主合作学习。五、教学中渗透态度情感培养。六、让反思成为习惯,让反思促进教学成长。
一节好课永远是有条件的,所以好课也是相对的。如同我们自己上一堂非常满意的课,但反思下来总有遗憾,总有可圈可点之处。即使运用同一教学评价标准,针对不同的地区,不同的课堂,不同的教师,评价结果还是会有差异的。总之,为了促进教师的提高和发展,是为鼓励教师完善自己的课堂。
