华师大版八年级数学上册 13.2.3 边角边 教案
文档属性
| 名称 | 华师大版八年级数学上册 13.2.3 边角边 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 284.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 16:21:11 | ||
图片预览

文档简介
三角形全等的判定(SAS)教案
一、教学目标:
1、知识与技能:⑴掌握边角边判定方法的内容,会运用边角边判定方法证明两三角形全等。
(2)掌握两边一角画三角形的方法。
(3)体会证明两线段相等,两个角相等通常转化为“证明两三角形全等”来解决的数学方法。
2、过程与方法:从动手操作到理性证明探索出三角形全等的判定方法:“边角边”。
3、情感态度与价值观:(1)培养学生的动手实践能力。
(2)培养学生严密的逻辑思维能力。
二、教学重点与难点:
1、重点:掌握三角形全等的判定方法——“边角边”。
2、难点:理解“边边角”不一定会全等,熟练运用“边角边”判定方法。
三、教学方法与手段:
1、教学方法:遵循“学生为主体,教师为主导”的教学原则,按照学生从感性认识到理性认识,从特殊到一般的认知规律,采用学生操作确认的方式及直观演示验证法,启发式引导学生展开思维、探究证明思路,循序渐进的教学方法。最大限度提高学生的参与率。
2、教学手段:借助于多媒体课件演示及学生动手操作确认发现新知。
四、教学过程:
复习引入:
上节课我们研究过两个三角形如果只知道有一组或两组元素对应相等,则这两个三角形不一定全等,而如果两个三角形有3组元素对应相等,这两个三角形很有可能全等。本节课要探究的问题是两条边及其一个角对应相等,两个三角形是否全等?
探究新知:探究一: 两边一角又会有哪几种情况?请同学们探讨一下!
探究二:两边及其夹角分别对应相等的两个三角形全等吗?
如图,已知两条线段和一个角,已这两条线段为边,以这个角为这两条边的夹角,画一个三角形。
画法:
1.画∠MAN= 45°
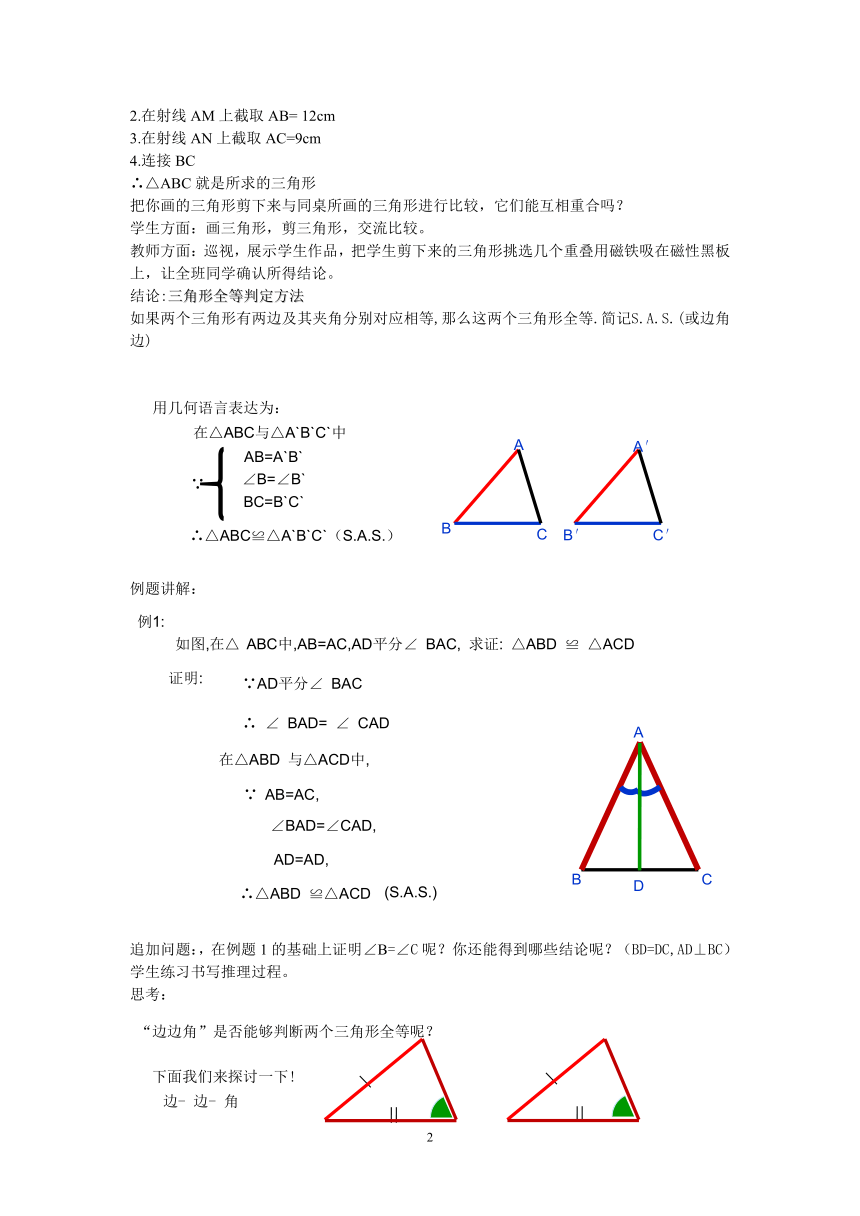
2.在射线AM上截取AB= 12cm
3.在射线AN上截取AC=9cm
4.连接BC
∴△ABC就是所求的三角形
把你画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
学生方面:画三角形,剪三角形,交流比较。
教师方面:巡视,展示学生作品,把学生剪下来的三角形挑选几个重叠用磁铁吸在磁性黑板上,让全班同学确认所得结论。
结论:三角形全等判定方法
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简记S.A.S.(或边角边)
例题讲解:
追加问题:,在例题1的基础上证明∠B=∠C呢?你还能得到哪些结论呢?(BD=DC,AD⊥BC)学生练习书写推理过程。
思考:
练习:
1.“如果两个三角形两条边和一个角对应相等,那么这两个三角形全等.”这个命题是真命题吗?你能举个反例说明吗?
答:△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠B
它们全等吗?
注:这个角一定要是这两边所夹的角
2.题中的两个三角形是否全等
答:BC≌△EFD 根据“SAS”
3.如图,在△AEC和△ADB中,已知AE=AD,AC=AB。请说明△AEC ≌ △ADB的理由。
解:在△AEC和△ADB中
AE =AD (已知)
∠A=∠A ( 公共角)
AC= AB ( 已知 )
∴ △AEC≌△ADB( SAS )
4:
已知:如图, AB=CB ,∠ ABD= ∠ CBD ,△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBD
边: AB=CB(已知)
角: ∠ABD= ∠CBD(已知)
边: ?
5. 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △OAD与△OBC全等的理由
五、课堂小结:
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
2.用SAS判定三角形全等的注意点:
(1)至少需要三个条件
(2)必须是两边一夹角(如不是夹角,则不一定全等)
(3)全等的三个条件必须是三角形的对应边和对应角,如条件不完整,则必须先证明三个条件
C′
∵
B′
C
B
A
A′
∴△ABC≌△A`B`C`(S.A.S.)
AB=A`B`
∠B=∠B`
BC=B`C`
在△ABC与△A`B`C`中
用几何语言表达为:
D
C
B
A
(S.A.S.)
∴△ABD ≌△ACD
AD=AD,
∵ AB=AC,
在△ABD 与△ACD中,
∴ ∠ BAD= ∠ CAD
∵AD平分∠ BAC
证明:
∠BAD=∠CAD,
例1:
如图,在△ ABC中,AB=AC,AD平分∠ BAC, 求证: △ABD ≌ △ACD
夹角
(1)边-角-边
(2)边-边-角
∵
解:在△OAD 和△OBC中
∴△OAD≌△OBC (S.A.S)
OA = OB(已知)
∠1 =∠2(对顶角等)
OD = OC (已知)
1
2
O
D
A
B
C
A
D
2.5cm
M
D
C
证明: 在等腰梯形ABCD中有
AD=BC, ∠ A= ∠ B
又∵点M是AB的中点
∴AM=BM
在△AMD和△BMC中
∵ AD=BC
∠ A= ∠ B
AM=BM
∴ △AMD≌△BMC
2、点M是等腰梯形ABCD底边AB的中点, 求证: △AMD≌△BMC
B
C
A
B
边- 边- 角
“边边角”是否能够判断两个三角形全等呢?
下面我们来探讨一下!
F
E
D
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
3.5cm
40°
40°
3.5cm
2.5cm
C
A
B
以3.5cm,2.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
PAGE
2
一、教学目标:
1、知识与技能:⑴掌握边角边判定方法的内容,会运用边角边判定方法证明两三角形全等。
(2)掌握两边一角画三角形的方法。
(3)体会证明两线段相等,两个角相等通常转化为“证明两三角形全等”来解决的数学方法。
2、过程与方法:从动手操作到理性证明探索出三角形全等的判定方法:“边角边”。
3、情感态度与价值观:(1)培养学生的动手实践能力。
(2)培养学生严密的逻辑思维能力。
二、教学重点与难点:
1、重点:掌握三角形全等的判定方法——“边角边”。
2、难点:理解“边边角”不一定会全等,熟练运用“边角边”判定方法。
三、教学方法与手段:
1、教学方法:遵循“学生为主体,教师为主导”的教学原则,按照学生从感性认识到理性认识,从特殊到一般的认知规律,采用学生操作确认的方式及直观演示验证法,启发式引导学生展开思维、探究证明思路,循序渐进的教学方法。最大限度提高学生的参与率。
2、教学手段:借助于多媒体课件演示及学生动手操作确认发现新知。
四、教学过程:
复习引入:
上节课我们研究过两个三角形如果只知道有一组或两组元素对应相等,则这两个三角形不一定全等,而如果两个三角形有3组元素对应相等,这两个三角形很有可能全等。本节课要探究的问题是两条边及其一个角对应相等,两个三角形是否全等?
探究新知:探究一: 两边一角又会有哪几种情况?请同学们探讨一下!
探究二:两边及其夹角分别对应相等的两个三角形全等吗?
如图,已知两条线段和一个角,已这两条线段为边,以这个角为这两条边的夹角,画一个三角形。
画法:
1.画∠MAN= 45°
2.在射线AM上截取AB= 12cm
3.在射线AN上截取AC=9cm
4.连接BC
∴△ABC就是所求的三角形
把你画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
学生方面:画三角形,剪三角形,交流比较。
教师方面:巡视,展示学生作品,把学生剪下来的三角形挑选几个重叠用磁铁吸在磁性黑板上,让全班同学确认所得结论。
结论:三角形全等判定方法
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简记S.A.S.(或边角边)
例题讲解:
追加问题:,在例题1的基础上证明∠B=∠C呢?你还能得到哪些结论呢?(BD=DC,AD⊥BC)学生练习书写推理过程。
思考:
练习:
1.“如果两个三角形两条边和一个角对应相等,那么这两个三角形全等.”这个命题是真命题吗?你能举个反例说明吗?
答:△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠B
它们全等吗?
注:这个角一定要是这两边所夹的角
2.题中的两个三角形是否全等
答:BC≌△EFD 根据“SAS”
3.如图,在△AEC和△ADB中,已知AE=AD,AC=AB。请说明△AEC ≌ △ADB的理由。
解:在△AEC和△ADB中
AE =AD (已知)
∠A=∠A ( 公共角)
AC= AB ( 已知 )
∴ △AEC≌△ADB( SAS )
4:
已知:如图, AB=CB ,∠ ABD= ∠ CBD ,△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBD
边: AB=CB(已知)
角: ∠ABD= ∠CBD(已知)
边: ?
5. 如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △OAD与△OBC全等的理由
五、课堂小结:
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
2.用SAS判定三角形全等的注意点:
(1)至少需要三个条件
(2)必须是两边一夹角(如不是夹角,则不一定全等)
(3)全等的三个条件必须是三角形的对应边和对应角,如条件不完整,则必须先证明三个条件
C′
∵
B′
C
B
A
A′
∴△ABC≌△A`B`C`(S.A.S.)
AB=A`B`
∠B=∠B`
BC=B`C`
在△ABC与△A`B`C`中
用几何语言表达为:
D
C
B
A
(S.A.S.)
∴△ABD ≌△ACD
AD=AD,
∵ AB=AC,
在△ABD 与△ACD中,
∴ ∠ BAD= ∠ CAD
∵AD平分∠ BAC
证明:
∠BAD=∠CAD,
例1:
如图,在△ ABC中,AB=AC,AD平分∠ BAC, 求证: △ABD ≌ △ACD
夹角
(1)边-角-边
(2)边-边-角
∵
解:在△OAD 和△OBC中
∴△OAD≌△OBC (S.A.S)
OA = OB(已知)
∠1 =∠2(对顶角等)
OD = OC (已知)
1
2
O
D
A
B
C
A
D
2.5cm
M
D
C
证明: 在等腰梯形ABCD中有
AD=BC, ∠ A= ∠ B
又∵点M是AB的中点
∴AM=BM
在△AMD和△BMC中
∵ AD=BC
∠ A= ∠ B
AM=BM
∴ △AMD≌△BMC
2、点M是等腰梯形ABCD底边AB的中点, 求证: △AMD≌△BMC
B
C
A
B
边- 边- 角
“边边角”是否能够判断两个三角形全等呢?
下面我们来探讨一下!
F
E
D
2.5cm
结论:两边及其一边所对的角相等,两个三角形不一定全等
3.5cm
40°
40°
3.5cm
2.5cm
C
A
B
以3.5cm,2.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?
PAGE
2
