华师大版八年级数学上册 14.1.2直角三角形的判定 教案
文档属性
| 名称 | 华师大版八年级数学上册 14.1.2直角三角形的判定 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 80.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 16:40:54 | ||
图片预览

文档简介
14.1.2直角三角形的判定
【教学目标】
1.探索勾股定理的逆定理,并能应用它解决简单的问题。
2.通过参与拼图、观察猜想、计算、推理归纳、证明等探究活动,体会探索数学问题的一般思路和方法,体会“数形结合”数学思想方法的应用。
3.在小组交流活动中培养合作、交流意识和探索精神,培养学生勇于展示自我的信心。
【教学重难点】
重点:探索勾股定理逆定理,并能应用它解决简单的问题。
难点:用同一法证明勾股定理逆定理。
【导学过程】
一、创设情境,导入课题
1.复习旧知:前面我们已经学习了直角三角形的定义和性质,按照研究问题的思路和方法,下面我们应该研究怎样判定一个三角形是直角三角形了,一个三角形满足什么条件才能是直角三角形呢 教学预设:
(1)有一个角是直角的三角形是直角三角形(利用定义);
(2)有两个角的和为90°的三角形是直角三角形;
这两种判定方法都是从“角”的数量关系上进行判定,从“边”上是否也可以进行直角三角形的判定呢
2.情景引入:首先让我们看看古埃及人怎样画直角.
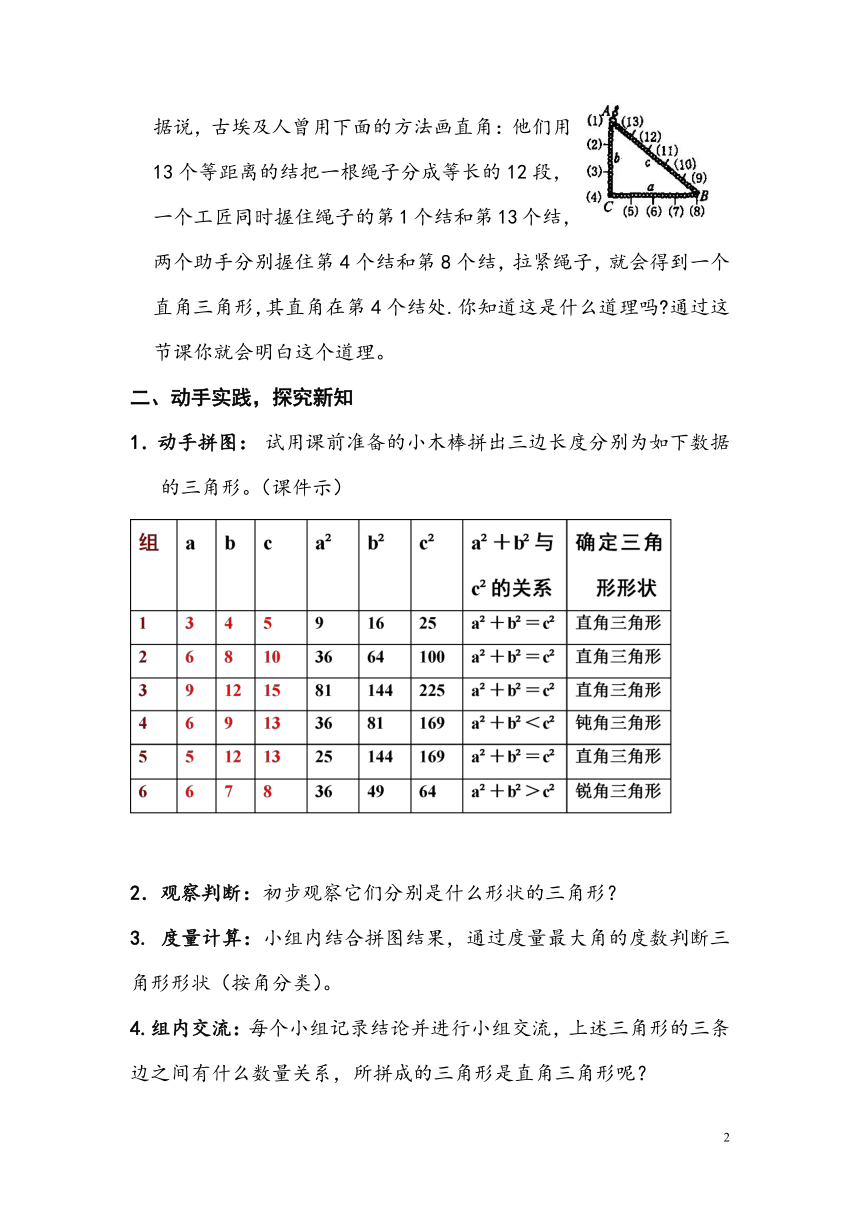
据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.你知道这是什么道理吗 通过这节课你就会明白这个道理。
二、动手实践,探究新知
1.动手拼图: 试用课前准备的小木棒拼出三边长度分别为如下数据的三角形。(课件示)
组 a b c a b c a +b 与c 的关系 确定三角形形状
1 3 4 5 9 16 25 a +b =c 直角三角形
2 6 8 10 36 64 100 a +b =c 直角三角形
3 9 12 15 81 144 225 a +b =c 直角三角形
4 6 9 13 36 81 169 a +b <c 钝角三角形
5 5 12 13 25 144 169 a +b =c 直角三角形
6 6 7 8 36 49 64 a +b >c 锐角三角形
2.观察判断:初步观察它们分别是什么形状的三角形?
3. 度量计算:小组内结合拼图结果,通过度量最大角的度数判断三角形形状(按角分类)。
4.组内交流:每个小组记录结论并进行小组交流,上述三角形的三条边之间有什么数量关系,所拼成的三角形是直角三角形呢?
5.尝试归纳:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形, 若a2+b2≠c2,则△ABC不是直角三角形.
(通过拼图观察、度量计算、猜想归纳,初步形成对拼出三角形形状的认识.)
6.理论证明:(在教师的引导下,学生自主完成理论证明,教师追问思路的形成过程)
已知:如图,在△ABC中,AB=c, BC=a, AC=b,a +b =c ,
求证:∠c=90° 课本113页
7.对比小结:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.且最长边c 所对的角是直角。
如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
(学生归纳之后老师总结,明确勾股定理的逆定理与勾股定理的互逆性,并渗透“数形结合”的数学思想)。
三、范例点击,提高认知
1.例1:判断由线段a,b,c组成的三角形是不是直角三角形 (课件示)
(1)a=7,b=25,c=24; (2) a=13,b=11,c=9
解:(1)最大边为25
∵a2+c2=72+242=49+576 =625
b2=252 =625
∴a2+c2= b 2
∴以7,25,24为边长的三角形是直角三角形.
(学生自己先尝试解决,然后教师规范解题过程,第2小题学生独立完成,并找一名学生展示自己的解题过程)。
2.问题回解:古埃及人画直角的方法原因,课件录音,两学生随录音展示过程,解释古埃及人画直角的方法。
3.例2、已知△ABC,AB=n -1,BC=2n,AC=n +1(n为大于1的正整数)(课本113页例题)(课件示)试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由。
(学生小组内部讨论尝试解决,一学生演板,之后师生共同评改。
教师点拨:对于上题中n的不同取值就可以得到不同的一组勾股数)。
4. 你出题我来答: 让学生在小组内举出三组数据,相互判断可否构成直角三角形,一小组长展示本组情况。
四、随堂练习,小组PK(课件示)
每个组抢答下面各题,每个小题标有相应的分值,抢到并答对的计入小组积分,(课堂记分员记录分)
1. 设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形。(4分)
(1) 1.5 ,2 ,2.5; (2) 5,6,7
2.若三角形三边为1, 2, 此三角形的形状是( )(3分)
A 锐角三角形 B 钝角三角形 C 直角三角形 D 无法判定
3.在△ABC中, a,b,c分别是 ∠A,∠B ,∠C的对边.若
a2+ c2 = b2 那个角是直角?(2分)
(通过练习巩固基本知识的掌握,小组PK提高学生参与的热情。)
五、课堂总结,畅谈收获
1.知识上:(1)判定一个三角形是直角三角形有哪些方法?
(2)勾股定理逆定理的内容及作用?
2.思想方法上:
(1)数形结合;
(2)探索数学问题的一般思路和方法:实验、观察、猜想、计算、推理、归纳、证明
(让同学们说出你有哪些收获?可让一学生回答,课堂记分员公布各小组得分情况,随后教师补充。并且总结每个小组课堂合作学习情况,给予鼓励和表彰。)
互逆定理
满足a2+b2=c2的三个正整数,称为一组勾股数.
如:3、4、5;5、12、13…
数形结合
思想
PAGE
5
【教学目标】
1.探索勾股定理的逆定理,并能应用它解决简单的问题。
2.通过参与拼图、观察猜想、计算、推理归纳、证明等探究活动,体会探索数学问题的一般思路和方法,体会“数形结合”数学思想方法的应用。
3.在小组交流活动中培养合作、交流意识和探索精神,培养学生勇于展示自我的信心。
【教学重难点】
重点:探索勾股定理逆定理,并能应用它解决简单的问题。
难点:用同一法证明勾股定理逆定理。
【导学过程】
一、创设情境,导入课题
1.复习旧知:前面我们已经学习了直角三角形的定义和性质,按照研究问题的思路和方法,下面我们应该研究怎样判定一个三角形是直角三角形了,一个三角形满足什么条件才能是直角三角形呢 教学预设:
(1)有一个角是直角的三角形是直角三角形(利用定义);
(2)有两个角的和为90°的三角形是直角三角形;
这两种判定方法都是从“角”的数量关系上进行判定,从“边”上是否也可以进行直角三角形的判定呢
2.情景引入:首先让我们看看古埃及人怎样画直角.
据说,古埃及人曾用下面的方法画直角:他们用13个等距离的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处.你知道这是什么道理吗 通过这节课你就会明白这个道理。
二、动手实践,探究新知
1.动手拼图: 试用课前准备的小木棒拼出三边长度分别为如下数据的三角形。(课件示)
组 a b c a b c a +b 与c 的关系 确定三角形形状
1 3 4 5 9 16 25 a +b =c 直角三角形
2 6 8 10 36 64 100 a +b =c 直角三角形
3 9 12 15 81 144 225 a +b =c 直角三角形
4 6 9 13 36 81 169 a +b <c 钝角三角形
5 5 12 13 25 144 169 a +b =c 直角三角形
6 6 7 8 36 49 64 a +b >c 锐角三角形
2.观察判断:初步观察它们分别是什么形状的三角形?
3. 度量计算:小组内结合拼图结果,通过度量最大角的度数判断三角形形状(按角分类)。
4.组内交流:每个小组记录结论并进行小组交流,上述三角形的三条边之间有什么数量关系,所拼成的三角形是直角三角形呢?
5.尝试归纳:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形, 若a2+b2≠c2,则△ABC不是直角三角形.
(通过拼图观察、度量计算、猜想归纳,初步形成对拼出三角形形状的认识.)
6.理论证明:(在教师的引导下,学生自主完成理论证明,教师追问思路的形成过程)
已知:如图,在△ABC中,AB=c, BC=a, AC=b,a +b =c ,
求证:∠c=90° 课本113页
7.对比小结:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形.且最长边c 所对的角是直角。
如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2.
(学生归纳之后老师总结,明确勾股定理的逆定理与勾股定理的互逆性,并渗透“数形结合”的数学思想)。
三、范例点击,提高认知
1.例1:判断由线段a,b,c组成的三角形是不是直角三角形 (课件示)
(1)a=7,b=25,c=24; (2) a=13,b=11,c=9
解:(1)最大边为25
∵a2+c2=72+242=49+576 =625
b2=252 =625
∴a2+c2= b 2
∴以7,25,24为边长的三角形是直角三角形.
(学生自己先尝试解决,然后教师规范解题过程,第2小题学生独立完成,并找一名学生展示自己的解题过程)。
2.问题回解:古埃及人画直角的方法原因,课件录音,两学生随录音展示过程,解释古埃及人画直角的方法。
3.例2、已知△ABC,AB=n -1,BC=2n,AC=n +1(n为大于1的正整数)(课本113页例题)(课件示)试问△ABC是直角三角形吗?若是,哪一条边所对的角是直角?请说明理由。
(学生小组内部讨论尝试解决,一学生演板,之后师生共同评改。
教师点拨:对于上题中n的不同取值就可以得到不同的一组勾股数)。
4. 你出题我来答: 让学生在小组内举出三组数据,相互判断可否构成直角三角形,一小组长展示本组情况。
四、随堂练习,小组PK(课件示)
每个组抢答下面各题,每个小题标有相应的分值,抢到并答对的计入小组积分,(课堂记分员记录分)
1. 设三角形三边长分别为下列各组数,试判断各三角形是否是直角三角形。(4分)
(1) 1.5 ,2 ,2.5; (2) 5,6,7
2.若三角形三边为1, 2, 此三角形的形状是( )(3分)
A 锐角三角形 B 钝角三角形 C 直角三角形 D 无法判定
3.在△ABC中, a,b,c分别是 ∠A,∠B ,∠C的对边.若
a2+ c2 = b2 那个角是直角?(2分)
(通过练习巩固基本知识的掌握,小组PK提高学生参与的热情。)
五、课堂总结,畅谈收获
1.知识上:(1)判定一个三角形是直角三角形有哪些方法?
(2)勾股定理逆定理的内容及作用?
2.思想方法上:
(1)数形结合;
(2)探索数学问题的一般思路和方法:实验、观察、猜想、计算、推理、归纳、证明
(让同学们说出你有哪些收获?可让一学生回答,课堂记分员公布各小组得分情况,随后教师补充。并且总结每个小组课堂合作学习情况,给予鼓励和表彰。)
互逆定理
满足a2+b2=c2的三个正整数,称为一组勾股数.
如:3、4、5;5、12、13…
数形结合
思想
PAGE
5
