幂函数[上学期]
图片预览





文档简介
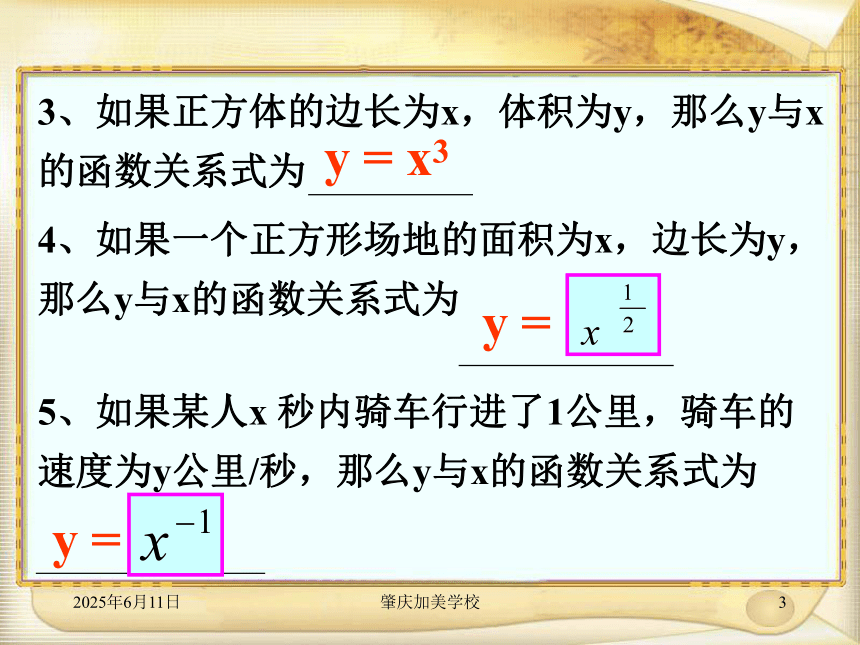
课件18张PPT。幂 函 数问 题y = xy = x22019年3月16日肇庆加美学校3y = x3y = y =2019年3月16日肇庆加美学校4?以上问题中的函数具有什么共同特征? 共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。新课一、幂函数的定义 一般地,函数y = xα叫做幂函数,其中x是自变量,α 是常数。注 意1、幂函数的解析式必须是y = xα 的形式,不能有一点差异。其特征可归纳为“两个1”,即:系数为1,只有1项。 2、幂函数的解析式 y = xα与指数函数的解析式 y = ax 的异同点。2019年3月16日肇庆加美学校6例1、下面几个函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=x2 + x (4)y=1
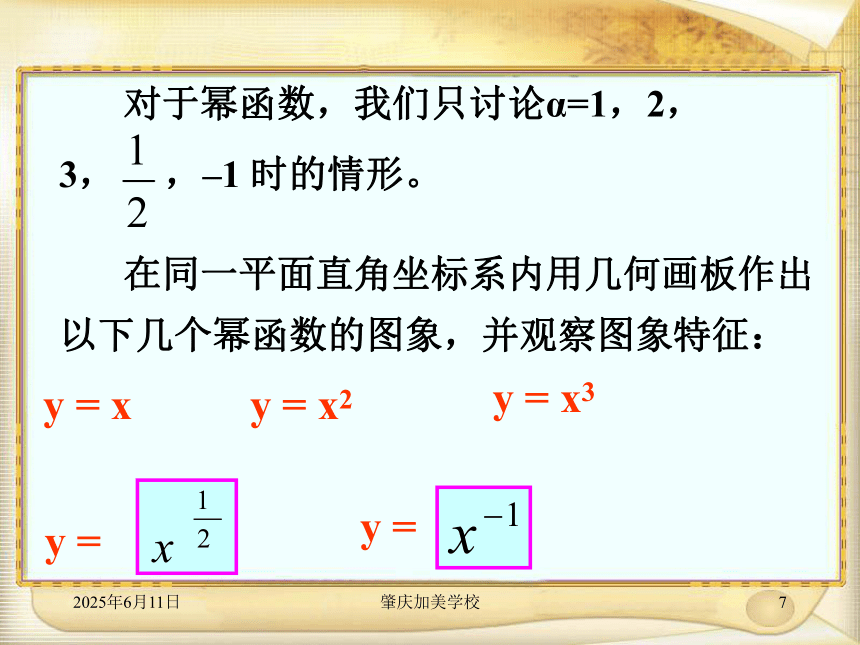
(5)y = 2x 答案(1)(4)2019年3月16日肇庆加美学校7 对于幂函数,我们只讨论α=1,2,3, ,–1 时的情形。探 究 请同学们观察课本第86页图2.3.1幂函数的图象,将你发现的结论填在下面(课本第86页) 的表格内:y = xy = y =RRR[0,+∞){x| x ≠ 0}R[0,+∞)R[0,+∞){y| y≠ 0}奇函数偶函数奇函数非奇非偶函数奇函数在(-∞,0]和(0, +∞)上都是增函数在(-∞,0]上是减函数,在(0, +∞)上是增函数在(-∞,0]和(0, +∞)上都是增函数在(0,+∞)上是增函数在( -∞,0)和(0, +∞)上都是减函数(1,1)奇偶性y = x22019年3月16日肇庆加美学校9 例2、已知幂函数y = f (x)的图象经过点(3 , ),求这个函数的解析式。2019年3月16日肇庆加美学校10例3、用不等号填空:<<>>≤<(4)2019年3月16日肇庆加美学校11 例4、如果函数
f (x) = (m2-m-1) 是幂函数,且在区间(0,+∞)上是减函数,求满足条件的实数m的集合。
2019年3月16日肇庆加美学校12尝 试 练 习 2、若幂函数 在 上是减函数,则( )B1、 的大小关系是( )
A、c<a<b B、 a<c<b
C、 b<a<c D、 c<b<aD2019年3月16日肇庆加美学校132019年3月16日肇庆加美学校14小 结1、幂函数的定义2、幂函数的图象特征和函数性质3、一般地,幂函数的图象在直线x=1的右侧,大指在上,小指在下,在Y轴与直线x =1之间正好相反。 4、应用函数性质解题时,要考虑数形结合,借助图象帮助思考。 2019年3月16日肇庆加美学校15探 究 与 发 现4、讨论函数 的定义域、值域、奇偶性,作出它的图象,并根据图象说明函数的单调性。 2019年3月16日肇庆加美学校16作 业
1、课本第87页第2、3题
2、在同一坐标系内,作出下列函数的图象,你能发现什么规律? 2019年3月16日肇庆加美学校17课 外 活 动 利用计算机探索一般幂函数 的图象随 的变化规律。 收 获 与 体 会 1、幂函数与指数函数的不同点主要表现在哪些方面?
2、怎样求幂函数的定义域?
3、五个基本幂函数的定义域与奇偶性、单调性之间的关系?再见!
(1)y = (2)y=2x2
(3)y=x2 + x (4)y=1
(5)y = 2x 答案(1)(4)2019年3月16日肇庆加美学校7 对于幂函数,我们只讨论α=1,2,3, ,–1 时的情形。探 究 请同学们观察课本第86页图2.3.1幂函数的图象,将你发现的结论填在下面(课本第86页) 的表格内:y = xy = y =RRR[0,+∞){x| x ≠ 0}R[0,+∞)R[0,+∞){y| y≠ 0}奇函数偶函数奇函数非奇非偶函数奇函数在(-∞,0]和(0, +∞)上都是增函数在(-∞,0]上是减函数,在(0, +∞)上是增函数在(-∞,0]和(0, +∞)上都是增函数在(0,+∞)上是增函数在( -∞,0)和(0, +∞)上都是减函数(1,1)奇偶性y = x22019年3月16日肇庆加美学校9 例2、已知幂函数y = f (x)的图象经过点(3 , ),求这个函数的解析式。2019年3月16日肇庆加美学校10例3、用不等号填空:<<>>≤<(4)2019年3月16日肇庆加美学校11 例4、如果函数
f (x) = (m2-m-1) 是幂函数,且在区间(0,+∞)上是减函数,求满足条件的实数m的集合。
2019年3月16日肇庆加美学校12尝 试 练 习 2、若幂函数 在 上是减函数,则( )B1、 的大小关系是( )
A、c<a<b B、 a<c<b
C、 b<a<c D、 c<b<aD2019年3月16日肇庆加美学校132019年3月16日肇庆加美学校14小 结1、幂函数的定义2、幂函数的图象特征和函数性质3、一般地,幂函数的图象在直线x=1的右侧,大指在上,小指在下,在Y轴与直线x =1之间正好相反。 4、应用函数性质解题时,要考虑数形结合,借助图象帮助思考。 2019年3月16日肇庆加美学校15探 究 与 发 现4、讨论函数 的定义域、值域、奇偶性,作出它的图象,并根据图象说明函数的单调性。 2019年3月16日肇庆加美学校16作 业
1、课本第87页第2、3题
2、在同一坐标系内,作出下列函数的图象,你能发现什么规律? 2019年3月16日肇庆加美学校17课 外 活 动 利用计算机探索一般幂函数 的图象随 的变化规律。 收 获 与 体 会 1、幂函数与指数函数的不同点主要表现在哪些方面?
2、怎样求幂函数的定义域?
3、五个基本幂函数的定义域与奇偶性、单调性之间的关系?再见!
