苏教版 五年级数学上册 8.6钉子板上的多边形 教案
文档属性
| 名称 | 苏教版 五年级数学上册 8.6钉子板上的多边形 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 74.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 11:43:00 | ||
图片预览

文档简介
钉子板上的多边形
教学内容:五年级上册p108-109“钉子板上的多边形”。
教学目标:1、使学生探索并发现钉子板上围成的多边形的面积,与围成的多边形边上的钉子数、多边形内部钉子数之间的关系,并尝试用字母式子表示关系。
2、使学生经历探索钉子板上围成的多边形面积与相关钉子数间的关系的过程,体会规律的复杂性和全面性,体会归纳思维,体会用字母表示关系的简洁性,发展观察、比较、推理、综合和抽象、概括等思维能力。
3、使学生获得探索规律成功的体验,树立学习数学的自信心,感受数学规律的奇妙,对数学产生好奇心,提高学习数学的兴趣和积极性。
教学重点:探索钉子板上多边形的面积与多边形边上钉子数、内部钉子数之间的关系
教学难点:综合、归纳多边形的面积与多边形边上钉子数、内部钉子数之间的关系。
学情分析:尽管是小学高段的学生,面对这样复杂的规律,孩子们仍然需要借助“形”来理解“数”。学生说各自的发现时,得出猜测S=n÷2-1,整节课还安排学生自我探究环节,学生自己去画图形结合图形区探索。除了“数形结合”,还注重“符号”思想。本节课在配合图形展示画、看、想、说的同时,一开始就明确用字母S和n表示图形面积数和图形边上钉子数,然后请学生尝试写出用含n的式子表示S。这也包括后来学生自觉用a表示图形内部钉子数。
一、求积导入
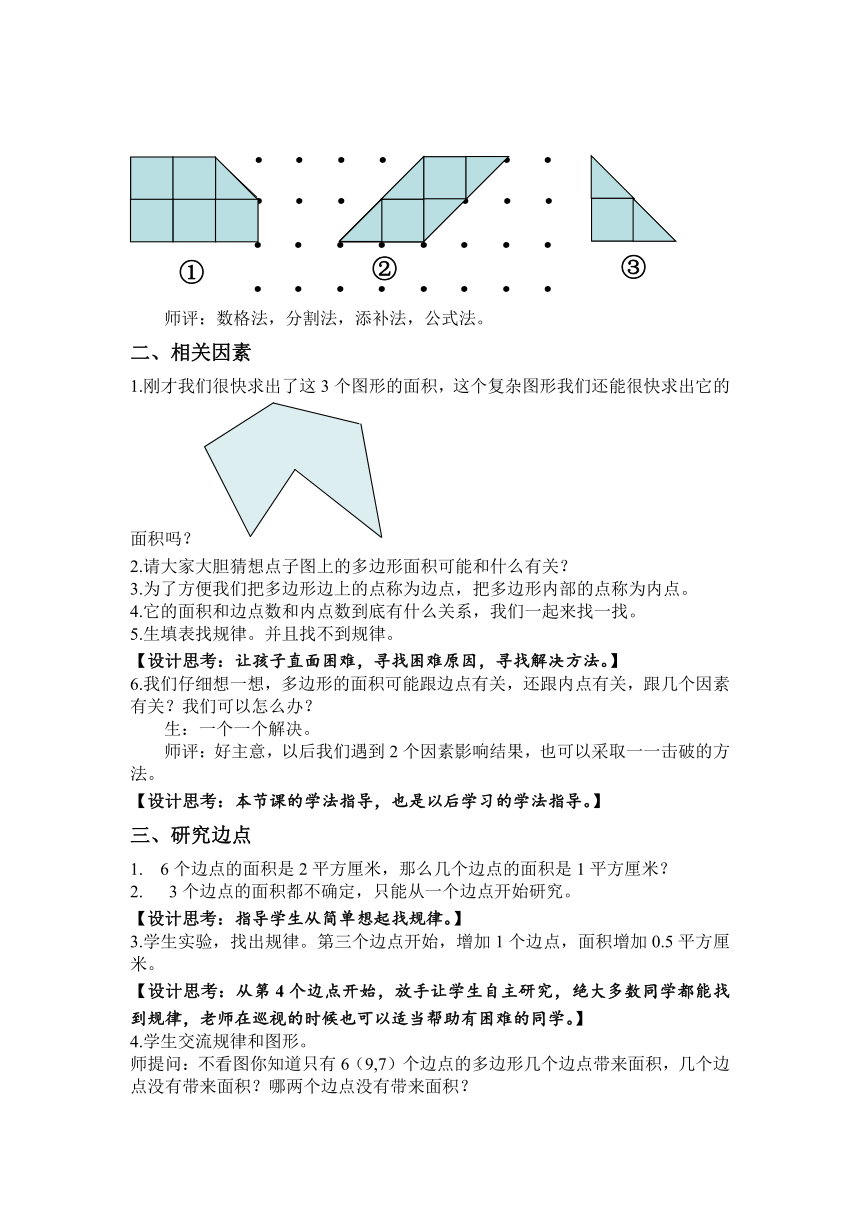
1.同学们,今天我们一起来研究《钉子板上的多边形》的面积。(板书)如果把钉子都变成点,大家还看得懂吗?每相邻两个钉子之间的距离都是1cm,相邻4个点围成一个面积是1cm 。
【设计思考:上课伊始,开门见山,告诉孩子研究钉子板上的多边形的面积。】
2.你会求这三个图形的面积吗?
师评:数格法,分割法,添补法,公式法。
二、相关因素
1.刚才我们很快求出了这3个图形的面积,这个复杂图形我们还能很快求出它的面积吗?
2.请大家大胆猜想点子图上的多边形面积可能和什么有关?
3.为了方便我们把多边形边上的点称为边点,把多边形内部的点称为内点。
4.它的面积和边点数和内点数到底有什么关系,我们一起来找一找。
5.生填表找规律。并且找不到规律。
【设计思考:让孩子直面困难,寻找困难原因,寻找解决方法。】
6.我们仔细想一想,多边形的面积可能跟边点有关,还跟内点有关,跟几个因素有关?我们可以怎么办?
生:一个一个解决。
师评:好主意,以后我们遇到2个因素影响结果,也可以采取一一击破的方法。
【设计思考:本节课的学法指导,也是以后学习的学法指导。】
三、研究边点
1. 6个边点的面积是2平方厘米,那么几个边点的面积是1平方厘米?
2. 3个边点的面积都不确定,只能从一个边点开始研究。
【设计思考:指导学生从简单想起找规律。】
3.学生实验,找出规律。第三个边点开始,增加1个边点,面积增加0.5平方厘米。
【设计思考:从第4个边点开始,放手让学生自主研究,绝大多数同学都能找到规律,老师在巡视的时候也可以适当帮助有困难的同学。】
4.学生交流规律和图形。
师提问:不看图你知道只有6(9,7)个边点的多边形几个边点带来面积,几个边点没有带来面积?哪两个边点没有带来面积?
5.电脑演示
10个边点的多边形有几个0.5?为什么要减2?20个边点呢?100个呢?
6字母表示:L个边点的多边形有几个0.5?为什么?
四、研究内点
1.回头再来看这张表格,看看有没有什么发现?
2.生计算边点带来的面积,再算剩余面积。
3.说说你们有发现?一个内点带来面积1平方厘米
4.到底对不对?
我们能不能设计一个多边形,验证增加1个内点增加面积1平方厘米?
因为找不到只有内点的多边形,所以老师给你提供了一个边点是6,内点是0的多边形。
你要验证1个内点带来面积1平方厘米,那么你设计的图形应该几个内点?
5.我们要研究内点,要不要让边点来影响面积?所以边点数能不能变?
具体指导:你准备让哪个点变成内点?
6.学生实验交流。
7.得出结论:如果有几个内点,面积就会增加N×1。
五、总公式
1、如果一个图形有L个边点,有N个内点,可以怎样求它的面积?
(L-2)×0.5+N×1
2、如果大家不放心,还可以用一个图形来验证这个公式对不对。
3、这个公式确定是正确的,此处应有掌声,这掌声送给谁?
应该送给这个奥地利的数学家。
4、我们的公式和他的公式一样吗?此处应该有热烈的掌声送给你们自己。我们是小小数学家。
六、求复杂图形
现在我们会求这个复杂图形的面积了吗?(上课开始的图形)
七、回顾过程,总结收获。
八、拓展
下图是等边三角形的点子图,每个等边三角形的面积都是1平方厘米,等边三角形点子图上的多边形面积和边点和内点有什么关系?
边点数 1 2 3 4 5 6
内点数 0 0 0 0 0 0
面 积
边点数 4 4 4 4 4
内点数 0 1 2 3 4
面 积
【设计思考:拓展题主要是方法的应用。】
【设计思考:这节课研究了钉子板上多边形面积与钉子数之间的关系。一开始学生面对复杂图形,大胆猜想出它的面积和边点和内点有关,学生想一起研究并没有成功,后来采取了一一击破的方法,在研究的过程中,学生从简单情形入手,通过画一画、数一数、算一算等方法,经历观察、比较、验证等活动,发现了规律。从上面的过程中同学们还真正找到每一个边点带来的面积,每一个内点带来的面积,这实际上是数形结合的方法。而表示数学规律一般用含有字母的式子,它具有简洁、明了、易记的特点。】
③
②
①
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
教学内容:五年级上册p108-109“钉子板上的多边形”。
教学目标:1、使学生探索并发现钉子板上围成的多边形的面积,与围成的多边形边上的钉子数、多边形内部钉子数之间的关系,并尝试用字母式子表示关系。
2、使学生经历探索钉子板上围成的多边形面积与相关钉子数间的关系的过程,体会规律的复杂性和全面性,体会归纳思维,体会用字母表示关系的简洁性,发展观察、比较、推理、综合和抽象、概括等思维能力。
3、使学生获得探索规律成功的体验,树立学习数学的自信心,感受数学规律的奇妙,对数学产生好奇心,提高学习数学的兴趣和积极性。
教学重点:探索钉子板上多边形的面积与多边形边上钉子数、内部钉子数之间的关系
教学难点:综合、归纳多边形的面积与多边形边上钉子数、内部钉子数之间的关系。
学情分析:尽管是小学高段的学生,面对这样复杂的规律,孩子们仍然需要借助“形”来理解“数”。学生说各自的发现时,得出猜测S=n÷2-1,整节课还安排学生自我探究环节,学生自己去画图形结合图形区探索。除了“数形结合”,还注重“符号”思想。本节课在配合图形展示画、看、想、说的同时,一开始就明确用字母S和n表示图形面积数和图形边上钉子数,然后请学生尝试写出用含n的式子表示S。这也包括后来学生自觉用a表示图形内部钉子数。
一、求积导入
1.同学们,今天我们一起来研究《钉子板上的多边形》的面积。(板书)如果把钉子都变成点,大家还看得懂吗?每相邻两个钉子之间的距离都是1cm,相邻4个点围成一个面积是1cm 。
【设计思考:上课伊始,开门见山,告诉孩子研究钉子板上的多边形的面积。】
2.你会求这三个图形的面积吗?
师评:数格法,分割法,添补法,公式法。
二、相关因素
1.刚才我们很快求出了这3个图形的面积,这个复杂图形我们还能很快求出它的面积吗?
2.请大家大胆猜想点子图上的多边形面积可能和什么有关?
3.为了方便我们把多边形边上的点称为边点,把多边形内部的点称为内点。
4.它的面积和边点数和内点数到底有什么关系,我们一起来找一找。
5.生填表找规律。并且找不到规律。
【设计思考:让孩子直面困难,寻找困难原因,寻找解决方法。】
6.我们仔细想一想,多边形的面积可能跟边点有关,还跟内点有关,跟几个因素有关?我们可以怎么办?
生:一个一个解决。
师评:好主意,以后我们遇到2个因素影响结果,也可以采取一一击破的方法。
【设计思考:本节课的学法指导,也是以后学习的学法指导。】
三、研究边点
1. 6个边点的面积是2平方厘米,那么几个边点的面积是1平方厘米?
2. 3个边点的面积都不确定,只能从一个边点开始研究。
【设计思考:指导学生从简单想起找规律。】
3.学生实验,找出规律。第三个边点开始,增加1个边点,面积增加0.5平方厘米。
【设计思考:从第4个边点开始,放手让学生自主研究,绝大多数同学都能找到规律,老师在巡视的时候也可以适当帮助有困难的同学。】
4.学生交流规律和图形。
师提问:不看图你知道只有6(9,7)个边点的多边形几个边点带来面积,几个边点没有带来面积?哪两个边点没有带来面积?
5.电脑演示
10个边点的多边形有几个0.5?为什么要减2?20个边点呢?100个呢?
6字母表示:L个边点的多边形有几个0.5?为什么?
四、研究内点
1.回头再来看这张表格,看看有没有什么发现?
2.生计算边点带来的面积,再算剩余面积。
3.说说你们有发现?一个内点带来面积1平方厘米
4.到底对不对?
我们能不能设计一个多边形,验证增加1个内点增加面积1平方厘米?
因为找不到只有内点的多边形,所以老师给你提供了一个边点是6,内点是0的多边形。
你要验证1个内点带来面积1平方厘米,那么你设计的图形应该几个内点?
5.我们要研究内点,要不要让边点来影响面积?所以边点数能不能变?
具体指导:你准备让哪个点变成内点?
6.学生实验交流。
7.得出结论:如果有几个内点,面积就会增加N×1。
五、总公式
1、如果一个图形有L个边点,有N个内点,可以怎样求它的面积?
(L-2)×0.5+N×1
2、如果大家不放心,还可以用一个图形来验证这个公式对不对。
3、这个公式确定是正确的,此处应有掌声,这掌声送给谁?
应该送给这个奥地利的数学家。
4、我们的公式和他的公式一样吗?此处应该有热烈的掌声送给你们自己。我们是小小数学家。
六、求复杂图形
现在我们会求这个复杂图形的面积了吗?(上课开始的图形)
七、回顾过程,总结收获。
八、拓展
下图是等边三角形的点子图,每个等边三角形的面积都是1平方厘米,等边三角形点子图上的多边形面积和边点和内点有什么关系?
边点数 1 2 3 4 5 6
内点数 0 0 0 0 0 0
面 积
边点数 4 4 4 4 4
内点数 0 1 2 3 4
面 积
【设计思考:拓展题主要是方法的应用。】
【设计思考:这节课研究了钉子板上多边形面积与钉子数之间的关系。一开始学生面对复杂图形,大胆猜想出它的面积和边点和内点有关,学生想一起研究并没有成功,后来采取了一一击破的方法,在研究的过程中,学生从简单情形入手,通过画一画、数一数、算一算等方法,经历观察、比较、验证等活动,发现了规律。从上面的过程中同学们还真正找到每一个边点带来的面积,每一个内点带来的面积,这实际上是数形结合的方法。而表示数学规律一般用含有字母的式子,它具有简洁、明了、易记的特点。】
③
②
①
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
