全等三角形的复习[上学期]
图片预览





文档简介
课件41张PPT。
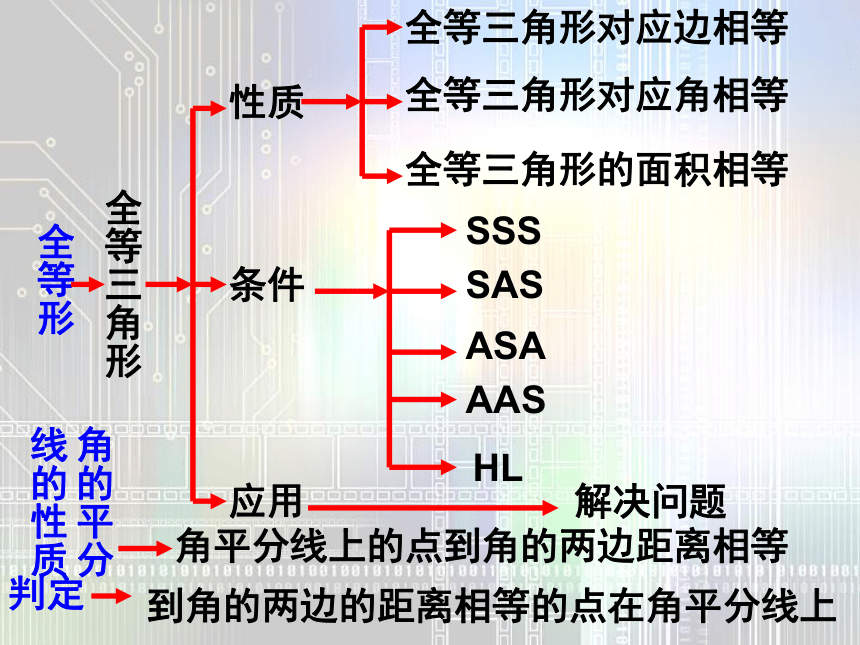
八年级数学第十三章全等三角形的复习全等形全等三角形性质条件应用全等三角形对应边相等全等三角形对应角相等全等三角形的面积相等SSSSASASAAASHL解决问题角的平分线的性质角平分线上的点到角的两边距离相等 到角的两边的距离相等的点在角平分线上判定知识点三角形全等的证题思路:全等三角形 ⑷证明两个三角形全等,要结合题目的条件和结论,选择恰当方法
⑸全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
④设法证明所缺的条件,有时所缺的条件可能在另一对全等三角形中,必须证两次全等。
⑤当要证的相等线段或角分别在两组以上的可能全等的三角形中,就应分析证明哪对三角形全等最好,一般选择条件具备多的一对较简单。
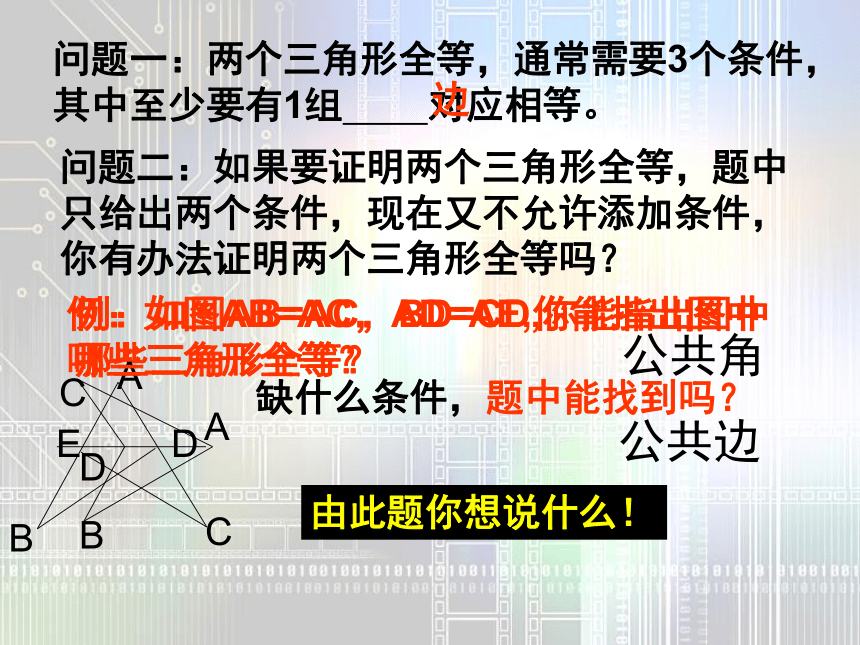
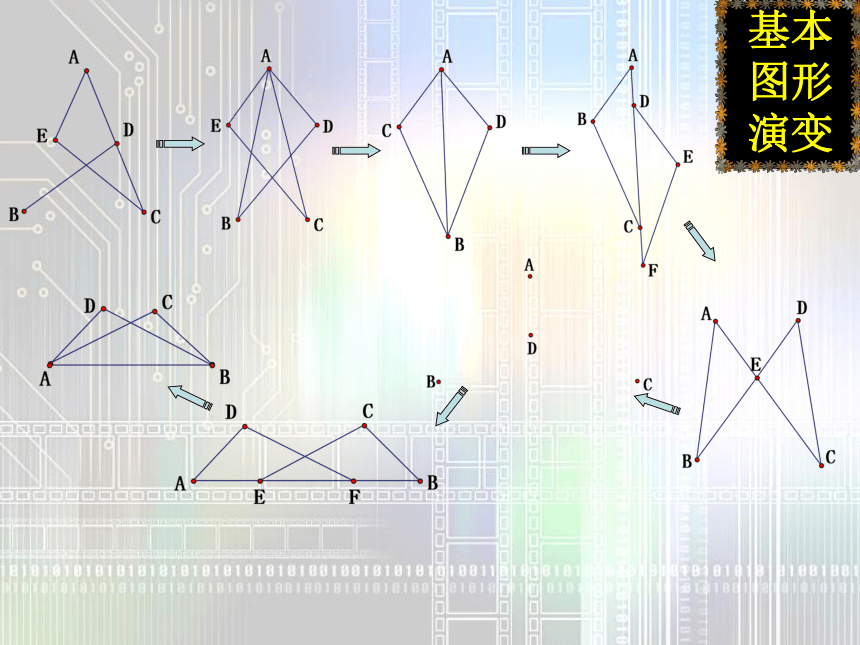
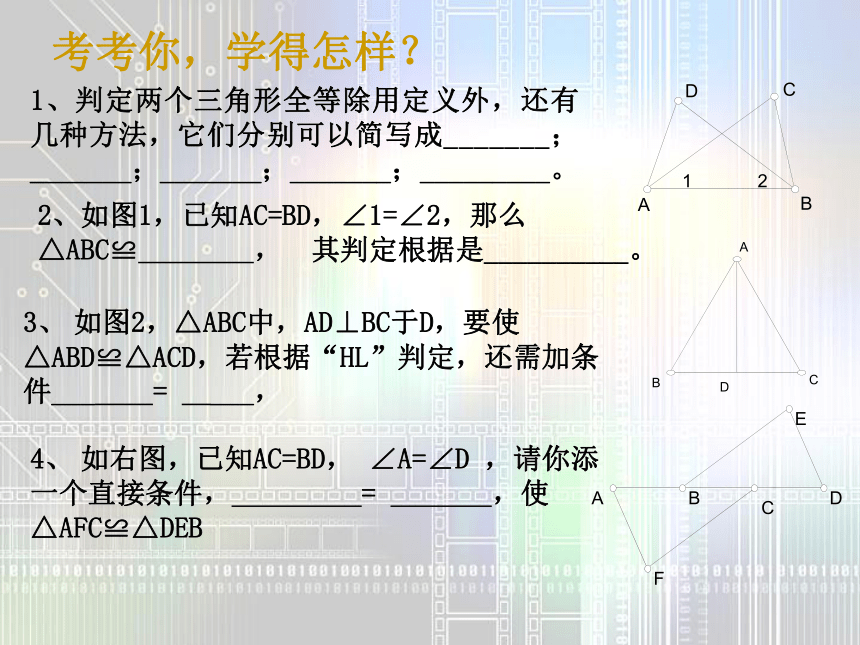
⑹有时证两线段相等,如存在角平分线且存在角平分线上的点到角的两边的垂线段就可直接用角平分线的性质定理来证,而不要去证三角形全等。 总之,证明过程中能用简单方法的就不要绕弯路。 问题一:两个三角形全等,通常需要3个条件,其中至少要有1组 对应相等。边问题二:如果要证明两个三角形全等,题中只给出两个条件,现在又不允许添加条件,你有办法证明两个三角形全等吗?缺什么条件,题中能找到吗?公共角由此题你想说什么!例:如图AB=AC,BD=CD,你能指出图中哪些三角形全等?公共边基本图形演变考考你,学得怎样?1、判定两个三角形全等除用定义外,还有几种方法,它们分别可以简写成_______;_______;_______;_______;_________。2、如图1,已知AC=BD,∠1=∠2,那么△ABC≌ , 其判定根据是__________。3、 如图2,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需加条件___ = ___,4、 如右图,已知AC=BD, ∠A=∠D ,请你添一个直接条件, = ,使△AFC≌△DEB5、如图,已知AB=AC,BE=CE,延长AE交BC于D,则图中全等三角形共有( )
(A)1对 (B)2对 (C)3对 (D)4对6、下列条件中,不能判定两个直角三角形全等的是( )
(A)一锐角和斜边对应相等 (B)两条直角边对应相等
(C)斜边和一直角边对应相等 (D)两个锐角对应相等7、下列四组中一定是全等三角形的为 ( )
A.三内角分别对应相等的两三角形
B、斜边相等的两直角三角形
C、两边和其中一条边的对角对应相等的两个三角形
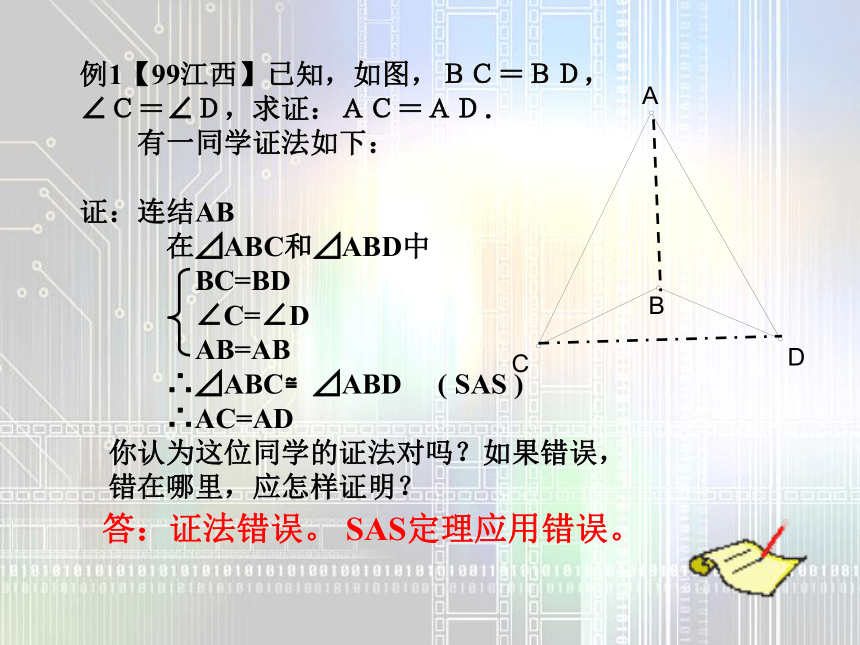
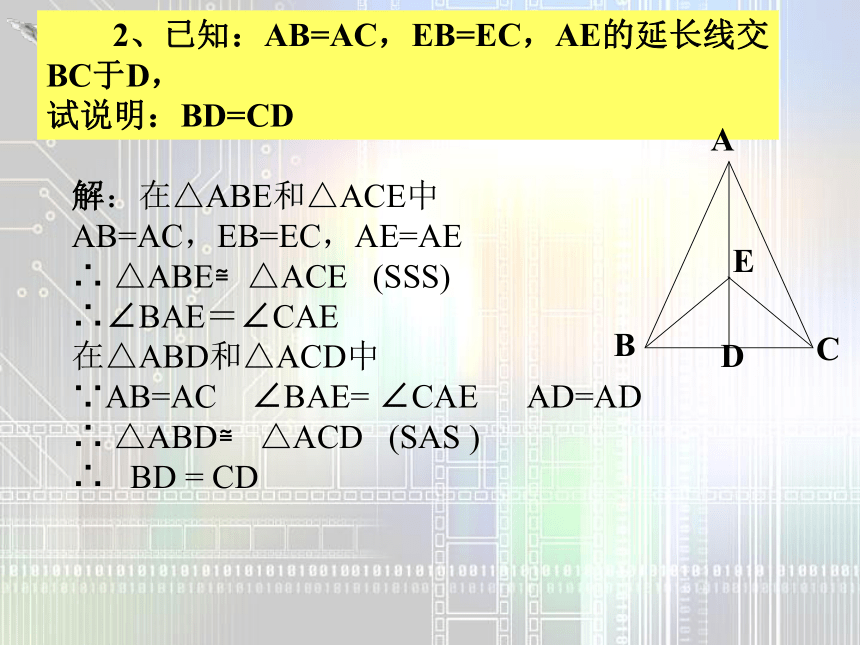
D、三边对应相等的两个三角形答:证法错误。 SAS定理应用错误。 2、已知:AB=AC,EB=EC,AE的延长线交BC于D,
试说明:BD=CD解:在△ABE和△ACE中
AB=AC,EB=EC,AE=AE
∴ △ABE≌△ACE (SSS)
∴∠BAE=∠CAE
在△ABD和△ACD中
∵AB=AC ∠BAE= ∠CAE AD=AD
∴ △ABD≌ △ACD (SAS )
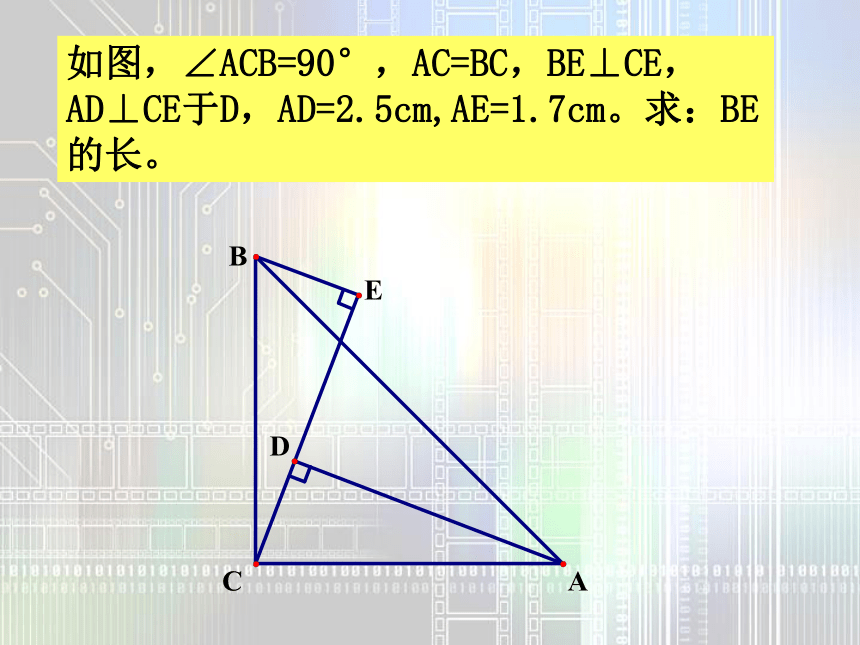
∴ BD = CD如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,AE=1.7cm。求:BE的长。试一试
已知:A、B两点之间被一个池塘隔开,无法直接测量A、B间的距离,请给出一个适合可行的方案,画出设计图,说明依据。ECDCDCD议一议如图,在△ABC中, ∠ACB=90°,AO是角平分线,点D在AC的延长线上,DE过点O且DE⊥AB,垂足为E.
(1) 请你找出图中一对相等的线段,并说明它们相等的理由; 解:∵∠ACB=90°
∴BC⊥AC
∵AO平分∠BAC
又DE⊥AB BC⊥AC
∴OE=OC(角平分线上的点到角两边的距离相等 (2)图中共有多少对相等线段,一一把它们找出来,
并说明理由 说一说: 在一次战役中,我军阵地与敌人碉堡隔河相望,需要知道碉堡与我军阵地的距离。在不能过河测量又没有任何测量工具的情况下,一个战士利用他头上的帽子就测出了我军阵地与敌人碉堡的距离。你知道他用的是什么方法?其中的原理是什么?1、 在三角形ABC中,已知AB=AC,且∠B=80° ,则∠C=——度,∠A=——度?2、 在三角形ABC中,已知AB=AC,且∠A=50° ,则∠B=——度,∠C=——度?3 、 在等腰三角形ABC中,如果AB=AC,且一个角等于70° ,求另两个角的度数。5、 在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?4、 在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠ A=______度?6、 在三角形ABC中,AB=AC=5cm,AD=4cm,且BD=CD,求点A到线段BC的距离。7、如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。8、 判断题(1) 等腰三角形 的底角都是鋭角 。 ( )
(2) 钝角三角形不可能是等腰三角形 。 ( )√ ×(3) 等腰直角三角形顶角是直角。 ( )√ 。( )×(1)如果AD⊥BC,∠BAD=25°,BD=4cm,
那么∠CAD=___, CD=___。(2)如果AD为中线,∠BAC=50°,那么
∠BAD=___ ,∠BDA=___ 。
3 填空:在△ABC中,AB=AC时
25°4cm25°90°4 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。 55°, 55°70°, 40°55°, 55°或70°, 40°40°, 40° 1、(1)如图,点D在AC上,
AB=BD=DC,∠C=400,
则∠A= 。
(2)如图,AD是等边
△ABC的中线,AD=AE,
则∠EDC= 。 400800800800150300DD12思考题等腰三角形底边中点到两腰的距离相等。方法1:证△FBD≌△ECD,得DE=DF
方法2:证△AED≌△AFD,得DE=DF方法3:利用面积相等来证明相等。 已知:如图,在△ABC中,AB=AC,D为BC边上的中点,DF⊥AB于F,DE ⊥ AC于E。
求证:DF=DE求证:等腰三角形两腰上的中线相等。 已知:如图,在△ABC中,AB=AC,BD和CE分别是AC、AB边上的中线。
求证:BD=CE。求证:等腰三角形两腰上的高线相等。 已知:如图,在△ABC中,AB=AC,BD⊥AC于D, CE⊥AB于E。
求证:BD=CE。
求证:等腰三角形底边上的高上的任意一点,到两腰 的距离相等。 求证:等腰三角形一腰上的高线与底 边的夹角等于顶角的一半。 例1.如图,在△ABC中,两条角平分线BD和CE相交于点哦,若∠BOC=1200,那么∠A的度数是 .600 例2、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点( )又∵AB=CD∴AE=CF在△ADE与△CBF中AE ==∴△ADE≌△CBF ( )∴AE= AB CF= CD( )例3.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )= 例4.如图,E,F在BC上,BE=CF,AB=CD,AB∥CD。求证:AF∥DE?ABF≌?DCE(SAS)∴∠AFB=∠DEC∴AF//DE∵ AB∥CD,AD∥BC(已知 )∴ ∠1=∠2 ∠3=∠4
在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)∴ △ABC≌△CDA(ASA)∴ AB=CD BC=AD(全等三角形对应边相等)证明:连结AC.例5.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD2341 例6.如图,已知AB=AD, ∠B=∠D,∠1=∠2,
求证:BC=DE证明:∵∠1=∠2∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠DAE在?ABC和?ADE中∴?ABC≌?ADE(AAS)∴BC=DE解∵ CE ⊥ AB,DF⊥ AC(已知)
∴ ∠ AEC= ∠ BFD=Rt∠
∵ AF=BE (已知)
即AE+EF=BF+EF
AE=BF
∵ AC=BD
∴ RtΔACE ≌ RtΔBDF(HL)
∴ CE=DF(全等三角形的对应边相等)ABCDEF 例7. 如图,已知CE ⊥AB,DF ⊥ AB,AC=BD,AF=BE,则CE=DF。请说明理由。 例8.已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DP
证明:在Rt?ABC和Rt?ABD中∴Rt?ABC≌Rt?ABD∴∠CAB=∠DAB∴?APC≌?APD(SAS)∴CP=DP?? 例9. 如图CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且∠1=∠2,求证OB=OC。 证明:∵∠1=∠2 CD⊥AB,BE⊥AC ∴OD=OE(角平分线的性质定理) 在△OBD与△OCE中 ∴△OBD≌△OCE(ASA) ∴OB=OC 例10. 如图A、B、C在一直线上,△ABD,△BCE都是等边三角形,AE交BD于F,DC交BE于G,求证:BF=BG。 证明:∵△ABD,△BCE是等边三角形。 ∴∠DBA=△EBC=60°
∵ A、B、C共线∴∠DBE=60° ∴∠ABE=∠DBC 在△ABE与△DBC中 ∴△ABE≌△DBC(SAS) ∴∠2=∠1 在△BEF与△BCG中 ∴△BEF≌△BCG(ASA) ∴BF=BG(全等三角形对应边相等)例11.如图AB//CD,∠B=90o,E是BC的中点,DE平分
∠ADC,求证:AE平分∠DABCDBAEF证明:作EF⊥AD,垂足为F
∵DE平分∠ADC
AB//CD,∴∠C=∠B
又∵∠B=90o∴∠C=90o又∵EF⊥AD
∴EF=CE
又∵E是BC的中点
∴EB=EC
∴EF=EB
∵∠B=90o
∴EB⊥AB
∴AE平分∠DAB∴BC⊥DC 例12. 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。∵AB=AC(已知)
AD=AD(公共边)∴Rt△ABD≌Rt△ACD(HL)∴BD=CD解:BD=CD∵ ∠ADB=∠ADC=90°同学们,再见!
八年级数学第十三章全等三角形的复习全等形全等三角形性质条件应用全等三角形对应边相等全等三角形对应角相等全等三角形的面积相等SSSSASASAAASHL解决问题角的平分线的性质角平分线上的点到角的两边距离相等 到角的两边的距离相等的点在角平分线上判定知识点三角形全等的证题思路:全等三角形 ⑷证明两个三角形全等,要结合题目的条件和结论,选择恰当方法
⑸全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
④设法证明所缺的条件,有时所缺的条件可能在另一对全等三角形中,必须证两次全等。
⑤当要证的相等线段或角分别在两组以上的可能全等的三角形中,就应分析证明哪对三角形全等最好,一般选择条件具备多的一对较简单。
⑹有时证两线段相等,如存在角平分线且存在角平分线上的点到角的两边的垂线段就可直接用角平分线的性质定理来证,而不要去证三角形全等。 总之,证明过程中能用简单方法的就不要绕弯路。 问题一:两个三角形全等,通常需要3个条件,其中至少要有1组 对应相等。边问题二:如果要证明两个三角形全等,题中只给出两个条件,现在又不允许添加条件,你有办法证明两个三角形全等吗?缺什么条件,题中能找到吗?公共角由此题你想说什么!例:如图AB=AC,BD=CD,你能指出图中哪些三角形全等?公共边基本图形演变考考你,学得怎样?1、判定两个三角形全等除用定义外,还有几种方法,它们分别可以简写成_______;_______;_______;_______;_________。2、如图1,已知AC=BD,∠1=∠2,那么△ABC≌ , 其判定根据是__________。3、 如图2,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需加条件___ = ___,4、 如右图,已知AC=BD, ∠A=∠D ,请你添一个直接条件, = ,使△AFC≌△DEB5、如图,已知AB=AC,BE=CE,延长AE交BC于D,则图中全等三角形共有( )
(A)1对 (B)2对 (C)3对 (D)4对6、下列条件中,不能判定两个直角三角形全等的是( )
(A)一锐角和斜边对应相等 (B)两条直角边对应相等
(C)斜边和一直角边对应相等 (D)两个锐角对应相等7、下列四组中一定是全等三角形的为 ( )
A.三内角分别对应相等的两三角形
B、斜边相等的两直角三角形
C、两边和其中一条边的对角对应相等的两个三角形
D、三边对应相等的两个三角形答:证法错误。 SAS定理应用错误。 2、已知:AB=AC,EB=EC,AE的延长线交BC于D,
试说明:BD=CD解:在△ABE和△ACE中
AB=AC,EB=EC,AE=AE
∴ △ABE≌△ACE (SSS)
∴∠BAE=∠CAE
在△ABD和△ACD中
∵AB=AC ∠BAE= ∠CAE AD=AD
∴ △ABD≌ △ACD (SAS )
∴ BD = CD如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,AE=1.7cm。求:BE的长。试一试
已知:A、B两点之间被一个池塘隔开,无法直接测量A、B间的距离,请给出一个适合可行的方案,画出设计图,说明依据。ECDCDCD议一议如图,在△ABC中, ∠ACB=90°,AO是角平分线,点D在AC的延长线上,DE过点O且DE⊥AB,垂足为E.
(1) 请你找出图中一对相等的线段,并说明它们相等的理由; 解:∵∠ACB=90°
∴BC⊥AC
∵AO平分∠BAC
又DE⊥AB BC⊥AC
∴OE=OC(角平分线上的点到角两边的距离相等 (2)图中共有多少对相等线段,一一把它们找出来,
并说明理由 说一说: 在一次战役中,我军阵地与敌人碉堡隔河相望,需要知道碉堡与我军阵地的距离。在不能过河测量又没有任何测量工具的情况下,一个战士利用他头上的帽子就测出了我军阵地与敌人碉堡的距离。你知道他用的是什么方法?其中的原理是什么?1、 在三角形ABC中,已知AB=AC,且∠B=80° ,则∠C=——度,∠A=——度?2、 在三角形ABC中,已知AB=AC,且∠A=50° ,则∠B=——度,∠C=——度?3 、 在等腰三角形ABC中,如果AB=AC,且一个角等于70° ,求另两个角的度数。5、 在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?4、 在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度∠ A=______度?6、 在三角形ABC中,AB=AC=5cm,AD=4cm,且BD=CD,求点A到线段BC的距离。7、如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。8、 判断题(1) 等腰三角形 的底角都是鋭角 。 ( )
(2) 钝角三角形不可能是等腰三角形 。 ( )√ ×(3) 等腰直角三角形顶角是直角。 ( )√ 。( )×(1)如果AD⊥BC,∠BAD=25°,BD=4cm,
那么∠CAD=___, CD=___。(2)如果AD为中线,∠BAC=50°,那么
∠BAD=___ ,∠BDA=___ 。
3 填空:在△ABC中,AB=AC时
25°4cm25°90°4 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。 55°, 55°70°, 40°55°, 55°或70°, 40°40°, 40° 1、(1)如图,点D在AC上,
AB=BD=DC,∠C=400,
则∠A= 。
(2)如图,AD是等边
△ABC的中线,AD=AE,
则∠EDC= 。 400800800800150300DD12思考题等腰三角形底边中点到两腰的距离相等。方法1:证△FBD≌△ECD,得DE=DF
方法2:证△AED≌△AFD,得DE=DF方法3:利用面积相等来证明相等。 已知:如图,在△ABC中,AB=AC,D为BC边上的中点,DF⊥AB于F,DE ⊥ AC于E。
求证:DF=DE求证:等腰三角形两腰上的中线相等。 已知:如图,在△ABC中,AB=AC,BD和CE分别是AC、AB边上的中线。
求证:BD=CE。求证:等腰三角形两腰上的高线相等。 已知:如图,在△ABC中,AB=AC,BD⊥AC于D, CE⊥AB于E。
求证:BD=CE。
求证:等腰三角形底边上的高上的任意一点,到两腰 的距离相等。 求证:等腰三角形一腰上的高线与底 边的夹角等于顶角的一半。 例1.如图,在△ABC中,两条角平分线BD和CE相交于点哦,若∠BOC=1200,那么∠A的度数是 .600 例2、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点( )又∵AB=CD∴AE=CF在△ADE与△CBF中AE ==∴△ADE≌△CBF ( )∴AE= AB CF= CD( )例3.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )= 例4.如图,E,F在BC上,BE=CF,AB=CD,AB∥CD。求证:AF∥DE?ABF≌?DCE(SAS)∴∠AFB=∠DEC∴AF//DE∵ AB∥CD,AD∥BC(已知 )∴ ∠1=∠2 ∠3=∠4
在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)∴ △ABC≌△CDA(ASA)∴ AB=CD BC=AD(全等三角形对应边相等)证明:连结AC.例5.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD2341 例6.如图,已知AB=AD, ∠B=∠D,∠1=∠2,
求证:BC=DE证明:∵∠1=∠2∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠DAE在?ABC和?ADE中∴?ABC≌?ADE(AAS)∴BC=DE解∵ CE ⊥ AB,DF⊥ AC(已知)
∴ ∠ AEC= ∠ BFD=Rt∠
∵ AF=BE (已知)
即AE+EF=BF+EF
AE=BF
∵ AC=BD
∴ RtΔACE ≌ RtΔBDF(HL)
∴ CE=DF(全等三角形的对应边相等)ABCDEF 例7. 如图,已知CE ⊥AB,DF ⊥ AB,AC=BD,AF=BE,则CE=DF。请说明理由。 例8.已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DP
证明:在Rt?ABC和Rt?ABD中∴Rt?ABC≌Rt?ABD∴∠CAB=∠DAB∴?APC≌?APD(SAS)∴CP=DP?? 例9. 如图CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且∠1=∠2,求证OB=OC。 证明:∵∠1=∠2 CD⊥AB,BE⊥AC ∴OD=OE(角平分线的性质定理) 在△OBD与△OCE中 ∴△OBD≌△OCE(ASA) ∴OB=OC 例10. 如图A、B、C在一直线上,△ABD,△BCE都是等边三角形,AE交BD于F,DC交BE于G,求证:BF=BG。 证明:∵△ABD,△BCE是等边三角形。 ∴∠DBA=△EBC=60°
∵ A、B、C共线∴∠DBE=60° ∴∠ABE=∠DBC 在△ABE与△DBC中 ∴△ABE≌△DBC(SAS) ∴∠2=∠1 在△BEF与△BCG中 ∴△BEF≌△BCG(ASA) ∴BF=BG(全等三角形对应边相等)例11.如图AB//CD,∠B=90o,E是BC的中点,DE平分
∠ADC,求证:AE平分∠DABCDBAEF证明:作EF⊥AD,垂足为F
∵DE平分∠ADC
AB//CD,∴∠C=∠B
又∵∠B=90o∴∠C=90o又∵EF⊥AD
∴EF=CE
又∵E是BC的中点
∴EB=EC
∴EF=EB
∵∠B=90o
∴EB⊥AB
∴AE平分∠DAB∴BC⊥DC 例12. 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。∵AB=AC(已知)
AD=AD(公共边)∴Rt△ABD≌Rt△ACD(HL)∴BD=CD解:BD=CD∵ ∠ADB=∠ADC=90°同学们,再见!
