2.3 简单的轴对称图形 同步练习(含答案)
文档属性
| 名称 | 2.3 简单的轴对称图形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-12 16:35:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
3 简单的轴对称图形
基础过关
知识点1 线段的轴对称性
1.线段是轴对称图形,它的对称轴有( )
A.1条 B.2条 C.3条 D.无数条
2.如图,AB的垂直平分线为直线MN,点P在MN上,连接PA,PB,则下列结论中,不一定正确的是( )
平分
3.如图,△ABC中, 14,边AB的垂直平分线和边AC的垂直平分线相交于点M,且与边BC相交于点D、E,连接AD、AE,则△AED的周长为( )
A.14 B.10 C.18 D.不能确定
4.如图,已知线段AB,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C、D两点,作直线CD,交AB于点E,在直线CD上任取一点F,连接FA、FB.若FA=5,则FB=_________.
5.如图,有A、B、C三个村,现在要建一个集贸市场,要求三个村到集贸市场的距离一样.请在图中确定集贸市场的位置.(保留作图痕迹)
知识点2 角的轴对称性
6.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是 ( )
A.PA=PB B.PO平分 C.OA=OB D.AB垂直平分OP
7.如图,AD是△ABC的角平分线.若 则点D到AC的距离是________.
知识点3 等腰三角形的性质及判定
8.若等腰三角形的两边长为5,10,则其周长为( )
A.15 B.20 C.25 D.20或25
9.如图,在△中,点D是边BC上的一点.若 则∠C的度数为__________.
10.如图,在△中, AD为△的角平分线,且 若△的周长为12,则△ABC的周长是____________.
11.如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
知识点4 等边三角形的性质及判定
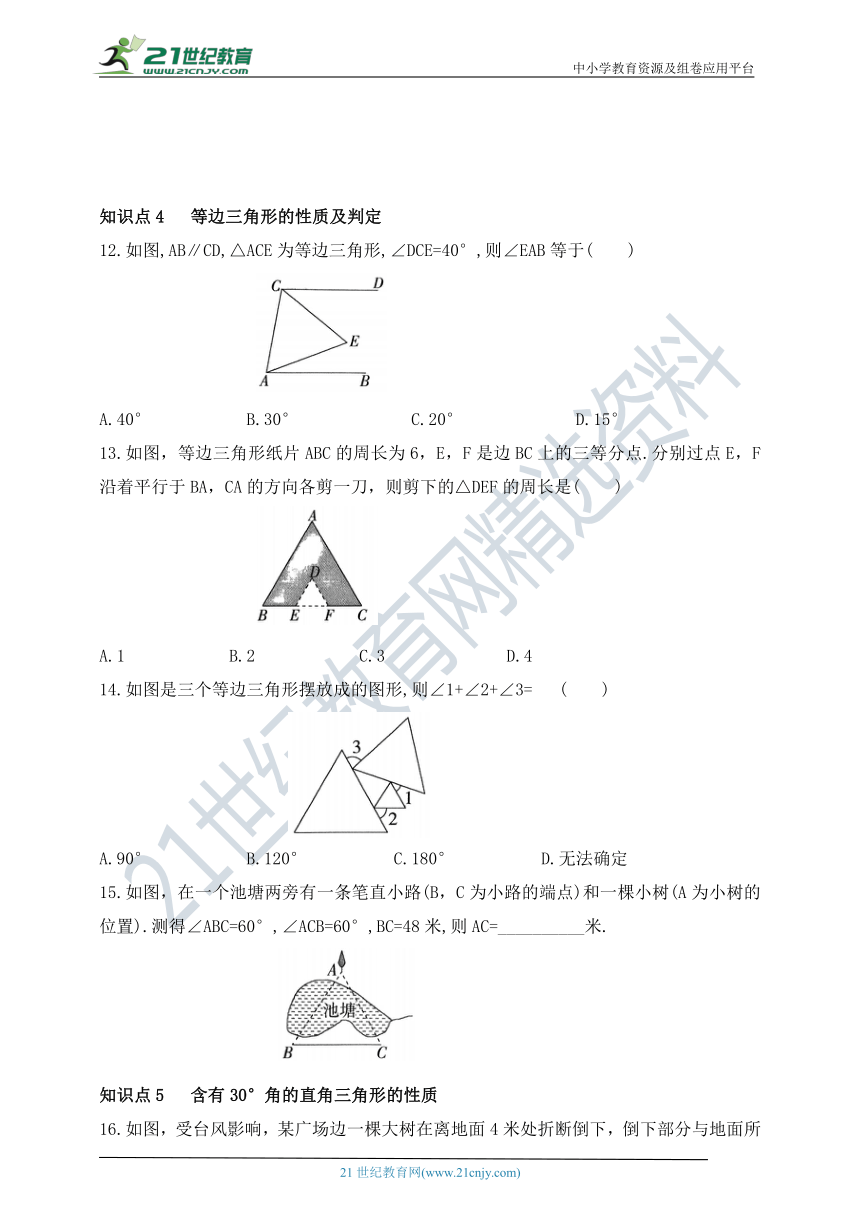
12.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
13.如图,等边三角形纸片ABC的周长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA的方向各剪一刀,则剪下的△DEF的周长是( )
A.1 B.2 C.3 D.4
14.如图是三个等边三角形摆放成的图形,则∠1+∠2+∠3= ( )
A.90° B.120° C.180° D.无法确定
15.如图,在一个池塘两旁有一条笔直小路(B,C为小路的端点)和一棵小树(A为小树的位置).测得∠ABC=60°,∠ACB=60°,BC=48米,则AC=__________米.
知识点5 含有30°角的直角三角形的性质
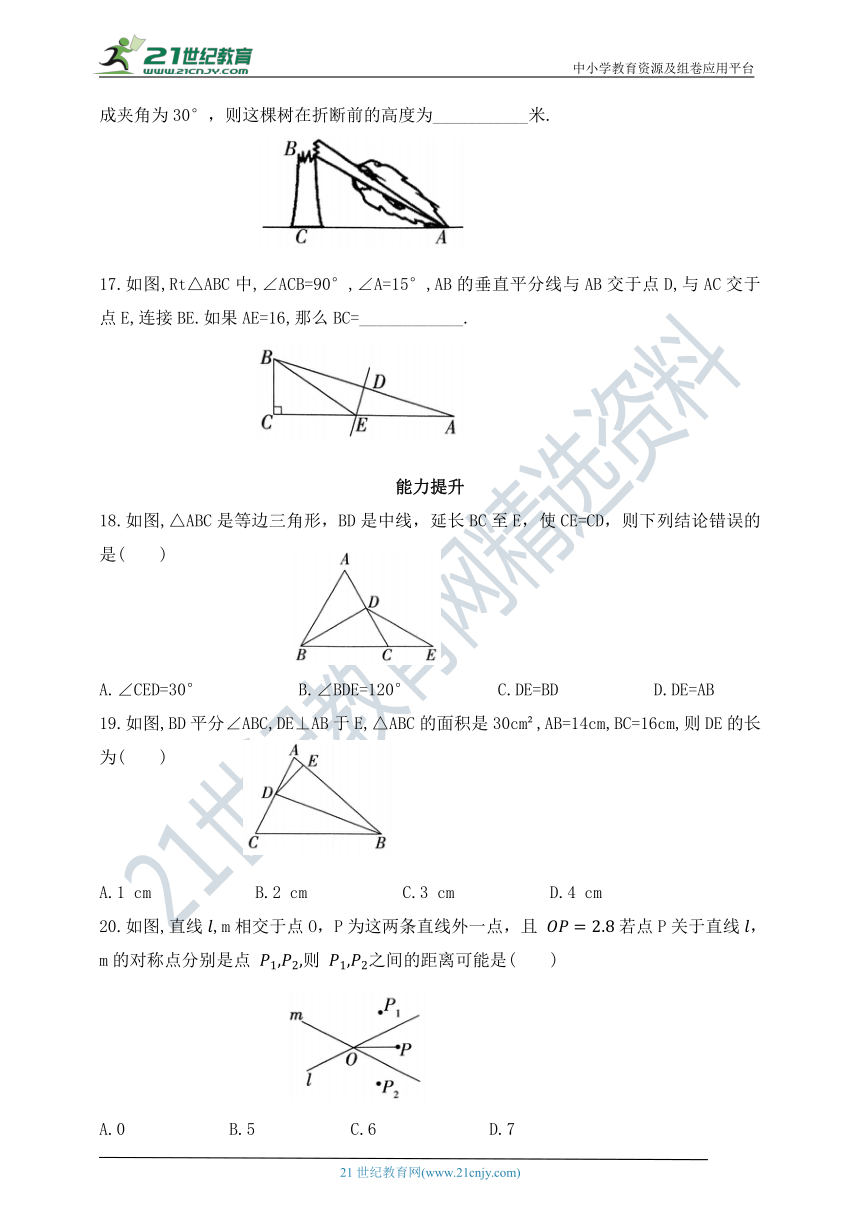
16.如图,受台风影响,某广场边一棵大树在离地面4米处折断倒下,倒下部分与地面所成夹角为30°,则这棵树在折断前的高度为___________米.
17.如图,Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AB交于点D,与AC交于点E,连接BE.如果AE=16,那么BC=____________.
能力提升
18.如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,则下列结论错误的是( )
A.∠CED=30° B.∠BDE=120° C.DE=BD D.DE=AB
19.如图,BD平分∠ABC,DE⊥AB于E,△ABC的面积是30cm ,AB=14cm,BC=16cm,则DE的长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
20.如图,直线,m相交于点O,P为这两条直线外一点,且 若点P关于直线,m的对称点分别是点 则 之间的距离可能是( )
A.0 B.5 C.6 D.7
21.如图,正方形网格中,点A,B是小正方形的顶点,如果点C是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )
A.6 B.7 C.8 D.9
22.下列说法:
(1)等腰三角形的高、中线、角平分线互相重合;
(2)等腰三角形的两腰上的中线长相等;
(3)等腰三角形的腰长一定大于其腰上的高;
(4)等腰三角形的两边长为8,16,那么它的周长是32或40.
其中不正确的个数是( )
A.1 B.2 C.3 D.4
23.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧,交AB于点D,连接CD,若 则∠BDC=( )
A.52° B.55° C.56° D.60°
24.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=4,DE=1.6,则BD的长为__________.
25.如图,在 中, 线段AB的垂直平分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为 _________.
26.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角的度数为__________.
27.[模型观念]如图,一艘旅游船从景观长廊AB的P处前往山脚下的Q处接游客,然后将游客送往河岸BC,再回到P处.请画出旅游船航行的最短路径.(实际航行路径画实线,其他辅助线画虚线)
28.[推理能力]数学课上,张老师举了下面的例题:
例1:等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:
例2:等腰三角形ABC中,∠A=40°,求∠B的度数.(答案: 或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式:等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题;
(2)小敏发现,∠A的度数不同,得到的 的度数的个数也可能不同,在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
参考答案
基础过关
1.B 线段所在的直线和过线段中点且与线段垂直的直线都是线段的对称轴,所以线段有2条对称轴.
2.C ∵AB的垂直平分线为直线MN,点P在MN上,∴PA=PB,OA=OB,又OP=OP,∴△AOP≌△BOP,∴ ∴PO平分∠APB.故选C.
3.A 因为直线DF是线段AB的垂直平分线,所以DA=DB,同理可得EA=EC,
所以△AED的周长=AD+DE+EA=BD+DE+EC=BC故选A.
4.答案 5
解析 由题意知直线CD是线段AB的垂直平分线,∵点F在直线CD上,∴FA=FB,∵FA=5,
5.解析 如图所示,连接AB、CA,作出AB、AC的垂直平分线,相交于点O,点O就是集贸市场的位置.
6.D 因为OP平分 所以 ,所以△所以∠APO=∠BPO,OA=OB,所以A,B,C中的结论一定成立,故选D.
7.答案 3
解析 如图,过点D作 于E,
因为AD是△ABC的角平分线,∠B=90°,DE⊥AC,所以DE=BD=3,所以点D到AC的距离为3.
8.C 分两种情况:①当腰长为5时,5+5=10,不能构成三角形;②当腰长为10时,5+10>10,能构成三角形,其周长是10+10+5=25.故选C.
9.答案 34°
解析 因为AB=AD,所以∠B=∠ADB,因为∠BAD=44°,所以
所以∠ADC=112°,因为AD=DC,所以 因为∠C+∠DAC+∠ADC=180°,所以∠C=34°.
10.答案 16
解析 因为AB=AC,所以△ABC是等腰三角形,因为AD为 的角平分线,所以BD=CD,又因为 的周长所以 所以△ABC的周长
11.解析 (1)证明:因为BD平分 所以∠ABD=∠CBD,因为 ∥所以 所以∠EBD=∠EDB,所以BE=DE.
(2)因为∠A=80°,∠C=40°,所以∠ABC=60°,因为BD平分∠ABC,所以∠ABD=∠CBD= 由(1)知∠EDB=∠EBD=30°.
12.C 因为AB∥CD,所以∠DCA+∠CAB=180°,即 因为△ACE为等边三角形,所以 所以 故选C.
13.B 因为等边三角形ABC的周长为6,所以 2, 因为E,F是边BC上的三等分点,所以 因为 所以 所以∠EDF=60°,所以△DEF是等边三角形,所以,所以△的周长 故选B.
14.C 如图,由题易知 因为 所以 ,故选C.
15.答案 48
解析 是等边三角形, 米.
16.答案 12
解析... 8米,∴这棵树在折断前的高度 12(米).
17.答案 8
解析 因为直线DE为线段AB的垂直平分线,所以BE=AE=16,所以∠EBA=∠A=15°,所以∠BEA=150°,所以 又因为 90°,所以
能力提升
18.D 因为 是等边三角形,BD是中线,所以所以 因为 所以 ∠CED.因为 所以所以 所以 故选D.
19.B 作 于F,如图,因为BD平分 所以 因为 所以 即所以 故选B.
20.B 如图,连接OP ,OP ,P P ,因为点P关于直线,m的对称点分别是点P ,P ,所以OP =OP=2.8,0P =OP=2.8,易知0<P P <5.6,故选B.
21.C 分情况讨论:①当AB为等腰△ABC的底边时,符合条件的点C有4个;②当AB为等腰△ABC的腰时,符合条件的点C有4个.综上,点C的个数为8,故选C.
22.C 等腰三角形的顶角的平分线、底边上的高、底边上的中线互相重合,故(1)错误;如图,△ABC是等腰三角形,AB=AC,BD、CE分别是边AC、AB上的中线.
因为 所以
在△BDC和△CEB中,所以△BDC≌△所以
故(2)正确;等腰直角三角形的腰长等于腰上的高,故(3)错误;因为等腰三角形的两边长为8,16,所以其三边长是16,16,8,所以它的周长是40,故(4)错误.故选C.
23.C 连接CH(图略),由题意得,直线MN是线段AB的垂直平分线, ∴∠BHC=44°,因为 故选C.
24.答案 2.4
解析 因为AD平分 所以CD=DE=1.6,所以BD=BC-CD=2.4.
25.答案 2
解析 因为DE垂直平分AB,所以AD=BD,所以∠ABD=∠A=30°,因为 所以∠ABC=60°,所以 所以2,所以
26.答案 或
解析 (1)如图①,△ABC中, 所以 易知 所以 因为 所以 所以∠B=360°;
(2)如图②, 中, 所以
所以
因为 所以4∠B=180°,所以∠B=45°.
综上,原等腰三角形的底角的度数为36°或45°.
27.解析 如图所示,连接PQ,作点P关于BC所在直线的对称点,连接 交BC于点M,连接MP.航行的最短路径为P—Q—M—P.
28.解析 (1)分三种情况:①当∠A为顶角时,∠B=
②当 是顶角时, 80°-80°=20°;③当 是顶角时,
综上所述,∠B的度数为 或 或
(2)分两种情况:①当 时, 只能为顶角,所以 的度数只有一个;
②当 )时,若 为顶角,则 若 为顶角,则 若 为顶角,则 当 且180-2x≠x且 即 时,∠B有三个不同的度数.综上所述,当 且x≠60时,∠B有三个不同的度数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 轴对称
3 简单的轴对称图形
基础过关
知识点1 线段的轴对称性
1.线段是轴对称图形,它的对称轴有( )
A.1条 B.2条 C.3条 D.无数条
2.如图,AB的垂直平分线为直线MN,点P在MN上,连接PA,PB,则下列结论中,不一定正确的是( )
平分
3.如图,△ABC中, 14,边AB的垂直平分线和边AC的垂直平分线相交于点M,且与边BC相交于点D、E,连接AD、AE,则△AED的周长为( )
A.14 B.10 C.18 D.不能确定
4.如图,已知线段AB,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于C、D两点,作直线CD,交AB于点E,在直线CD上任取一点F,连接FA、FB.若FA=5,则FB=_________.
5.如图,有A、B、C三个村,现在要建一个集贸市场,要求三个村到集贸市场的距离一样.请在图中确定集贸市场的位置.(保留作图痕迹)
知识点2 角的轴对称性
6.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是 ( )
A.PA=PB B.PO平分 C.OA=OB D.AB垂直平分OP
7.如图,AD是△ABC的角平分线.若 则点D到AC的距离是________.
知识点3 等腰三角形的性质及判定
8.若等腰三角形的两边长为5,10,则其周长为( )
A.15 B.20 C.25 D.20或25
9.如图,在△中,点D是边BC上的一点.若 则∠C的度数为__________.
10.如图,在△中, AD为△的角平分线,且 若△的周长为12,则△ABC的周长是____________.
11.如图,在△ABC中,∠ABC的平分线交AC于点D,过点D作DE∥BC交AB于点E.
(1)求证:BE=DE;
(2)若∠A=80°,∠C=40°,求∠BDE的度数.
知识点4 等边三角形的性质及判定
12.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
13.如图,等边三角形纸片ABC的周长为6,E,F是边BC上的三等分点.分别过点E,F沿着平行于BA,CA的方向各剪一刀,则剪下的△DEF的周长是( )
A.1 B.2 C.3 D.4
14.如图是三个等边三角形摆放成的图形,则∠1+∠2+∠3= ( )
A.90° B.120° C.180° D.无法确定
15.如图,在一个池塘两旁有一条笔直小路(B,C为小路的端点)和一棵小树(A为小树的位置).测得∠ABC=60°,∠ACB=60°,BC=48米,则AC=__________米.
知识点5 含有30°角的直角三角形的性质
16.如图,受台风影响,某广场边一棵大树在离地面4米处折断倒下,倒下部分与地面所成夹角为30°,则这棵树在折断前的高度为___________米.
17.如图,Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AB交于点D,与AC交于点E,连接BE.如果AE=16,那么BC=____________.
能力提升
18.如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,则下列结论错误的是( )
A.∠CED=30° B.∠BDE=120° C.DE=BD D.DE=AB
19.如图,BD平分∠ABC,DE⊥AB于E,△ABC的面积是30cm ,AB=14cm,BC=16cm,则DE的长为( )
A.1 cm B.2 cm C.3 cm D.4 cm
20.如图,直线,m相交于点O,P为这两条直线外一点,且 若点P关于直线,m的对称点分别是点 则 之间的距离可能是( )
A.0 B.5 C.6 D.7
21.如图,正方形网格中,点A,B是小正方形的顶点,如果点C是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )
A.6 B.7 C.8 D.9
22.下列说法:
(1)等腰三角形的高、中线、角平分线互相重合;
(2)等腰三角形的两腰上的中线长相等;
(3)等腰三角形的腰长一定大于其腰上的高;
(4)等腰三角形的两边长为8,16,那么它的周长是32或40.
其中不正确的个数是( )
A.1 B.2 C.3 D.4
23.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交AB于点H,以点H为圆心,HA的长为半径作的弧恰好经过点C,以点B为圆心,BC的长为半径作弧,交AB于点D,连接CD,若 则∠BDC=( )
A.52° B.55° C.56° D.60°
24.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=4,DE=1.6,则BD的长为__________.
25.如图,在 中, 线段AB的垂直平分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为 _________.
26.过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角的度数为__________.
27.[模型观念]如图,一艘旅游船从景观长廊AB的P处前往山脚下的Q处接游客,然后将游客送往河岸BC,再回到P处.请画出旅游船航行的最短路径.(实际航行路径画实线,其他辅助线画虚线)
28.[推理能力]数学课上,张老师举了下面的例题:
例1:等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:
例2:等腰三角形ABC中,∠A=40°,求∠B的度数.(答案: 或70°或100°)
张老师启发同学们进行变式,小敏编了如下一题:
变式:等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题;
(2)小敏发现,∠A的度数不同,得到的 的度数的个数也可能不同,在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
参考答案
基础过关
1.B 线段所在的直线和过线段中点且与线段垂直的直线都是线段的对称轴,所以线段有2条对称轴.
2.C ∵AB的垂直平分线为直线MN,点P在MN上,∴PA=PB,OA=OB,又OP=OP,∴△AOP≌△BOP,∴ ∴PO平分∠APB.故选C.
3.A 因为直线DF是线段AB的垂直平分线,所以DA=DB,同理可得EA=EC,
所以△AED的周长=AD+DE+EA=BD+DE+EC=BC故选A.
4.答案 5
解析 由题意知直线CD是线段AB的垂直平分线,∵点F在直线CD上,∴FA=FB,∵FA=5,
5.解析 如图所示,连接AB、CA,作出AB、AC的垂直平分线,相交于点O,点O就是集贸市场的位置.
6.D 因为OP平分 所以 ,所以△所以∠APO=∠BPO,OA=OB,所以A,B,C中的结论一定成立,故选D.
7.答案 3
解析 如图,过点D作 于E,
因为AD是△ABC的角平分线,∠B=90°,DE⊥AC,所以DE=BD=3,所以点D到AC的距离为3.
8.C 分两种情况:①当腰长为5时,5+5=10,不能构成三角形;②当腰长为10时,5+10>10,能构成三角形,其周长是10+10+5=25.故选C.
9.答案 34°
解析 因为AB=AD,所以∠B=∠ADB,因为∠BAD=44°,所以
所以∠ADC=112°,因为AD=DC,所以 因为∠C+∠DAC+∠ADC=180°,所以∠C=34°.
10.答案 16
解析 因为AB=AC,所以△ABC是等腰三角形,因为AD为 的角平分线,所以BD=CD,又因为 的周长所以 所以△ABC的周长
11.解析 (1)证明:因为BD平分 所以∠ABD=∠CBD,因为 ∥所以 所以∠EBD=∠EDB,所以BE=DE.
(2)因为∠A=80°,∠C=40°,所以∠ABC=60°,因为BD平分∠ABC,所以∠ABD=∠CBD= 由(1)知∠EDB=∠EBD=30°.
12.C 因为AB∥CD,所以∠DCA+∠CAB=180°,即 因为△ACE为等边三角形,所以 所以 故选C.
13.B 因为等边三角形ABC的周长为6,所以 2, 因为E,F是边BC上的三等分点,所以 因为 所以 所以∠EDF=60°,所以△DEF是等边三角形,所以,所以△的周长 故选B.
14.C 如图,由题易知 因为 所以 ,故选C.
15.答案 48
解析 是等边三角形, 米.
16.答案 12
解析... 8米,∴这棵树在折断前的高度 12(米).
17.答案 8
解析 因为直线DE为线段AB的垂直平分线,所以BE=AE=16,所以∠EBA=∠A=15°,所以∠BEA=150°,所以 又因为 90°,所以
能力提升
18.D 因为 是等边三角形,BD是中线,所以所以 因为 所以 ∠CED.因为 所以所以 所以 故选D.
19.B 作 于F,如图,因为BD平分 所以 因为 所以 即所以 故选B.
20.B 如图,连接OP ,OP ,P P ,因为点P关于直线,m的对称点分别是点P ,P ,所以OP =OP=2.8,0P =OP=2.8,易知0<P P <5.6,故选B.
21.C 分情况讨论:①当AB为等腰△ABC的底边时,符合条件的点C有4个;②当AB为等腰△ABC的腰时,符合条件的点C有4个.综上,点C的个数为8,故选C.
22.C 等腰三角形的顶角的平分线、底边上的高、底边上的中线互相重合,故(1)错误;如图,△ABC是等腰三角形,AB=AC,BD、CE分别是边AC、AB上的中线.
因为 所以
在△BDC和△CEB中,所以△BDC≌△所以
故(2)正确;等腰直角三角形的腰长等于腰上的高,故(3)错误;因为等腰三角形的两边长为8,16,所以其三边长是16,16,8,所以它的周长是40,故(4)错误.故选C.
23.C 连接CH(图略),由题意得,直线MN是线段AB的垂直平分线, ∴∠BHC=44°,因为 故选C.
24.答案 2.4
解析 因为AD平分 所以CD=DE=1.6,所以BD=BC-CD=2.4.
25.答案 2
解析 因为DE垂直平分AB,所以AD=BD,所以∠ABD=∠A=30°,因为 所以∠ABC=60°,所以 所以2,所以
26.答案 或
解析 (1)如图①,△ABC中, 所以 易知 所以 因为 所以 所以∠B=360°;
(2)如图②, 中, 所以
所以
因为 所以4∠B=180°,所以∠B=45°.
综上,原等腰三角形的底角的度数为36°或45°.
27.解析 如图所示,连接PQ,作点P关于BC所在直线的对称点,连接 交BC于点M,连接MP.航行的最短路径为P—Q—M—P.
28.解析 (1)分三种情况:①当∠A为顶角时,∠B=
②当 是顶角时, 80°-80°=20°;③当 是顶角时,
综上所述,∠B的度数为 或 或
(2)分两种情况:①当 时, 只能为顶角,所以 的度数只有一个;
②当 )时,若 为顶角,则 若 为顶角,则 若 为顶角,则 当 且180-2x≠x且 即 时,∠B有三个不同的度数.综上所述,当 且x≠60时,∠B有三个不同的度数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
