四川省邻水县2013年春季期末学科教学质量检测八年级数学(附答案)
文档属性
| 名称 | 四川省邻水县2013年春季期末学科教学质量检测八年级数学(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 108.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-10 22:46:31 | ||
图片预览


文档简介
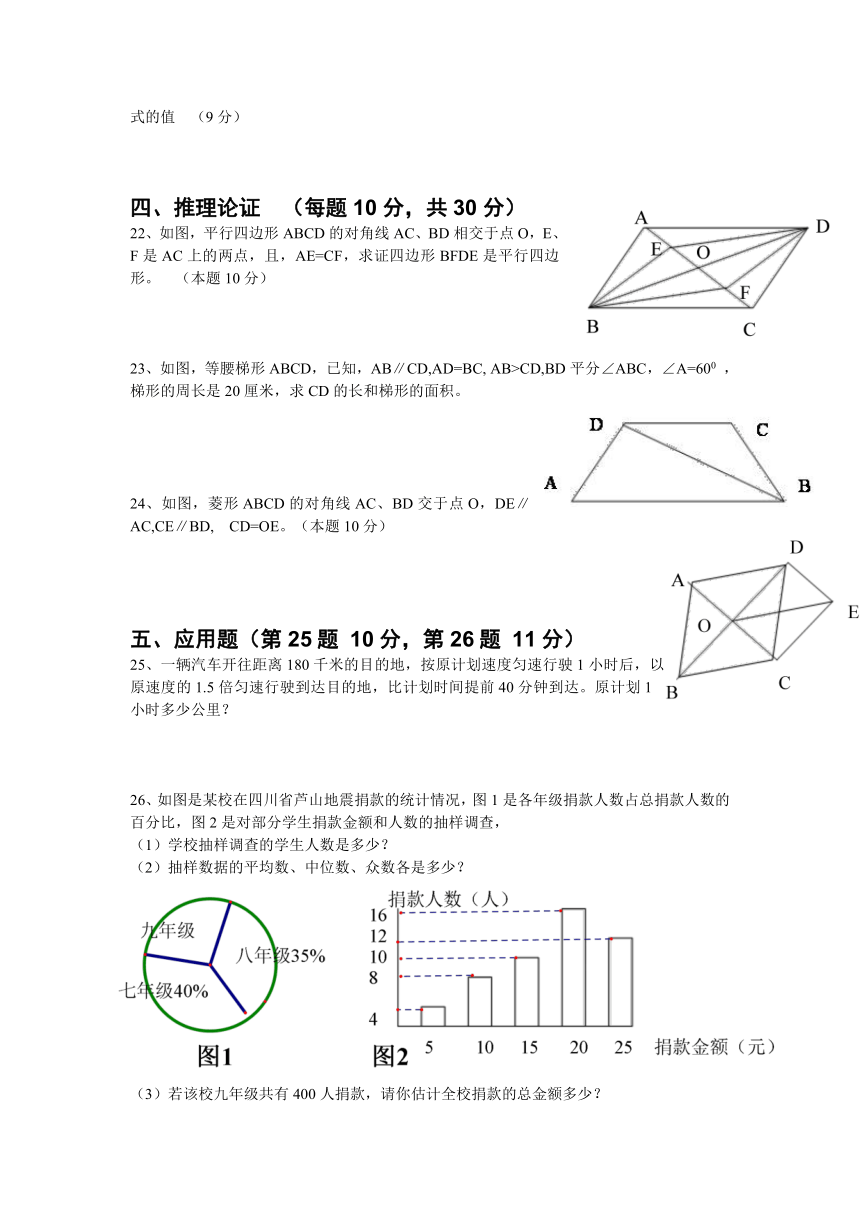
四川省邻水县2013年春季期末学科教学质量检测
八年级数学试卷
一、每题3分,共30分
1、甲、乙、丙三人进行射击测试,每人10次射击的平均成绩都是9.4环,方差分别是 , , ,在本次测试中成绩最稳定的是( )
A、甲 B、乙 C、丙 D、不确定
2、若一组数据33、28、27、、22、23的中位数是26,则数据中为( )
A、24 B、25 C、26 D、28
3、矩形的两条对角线夹角为600 ,对角线长为15厘米,则最短的边为( )
A、12㎝ B、10㎝ C、7.5㎝ D、5㎝
4、下列说法错误的是 ( )
A、对角线互相垂直的四边形是菱形;
B、对角线互相垂直平分且相等的四边形是正方形;
C、对角线相等的平行四边形是矩形;
D、一组对边平行,一组对角相等的四边形是平行四边形。
5、不改变分式的值,把分式的分子和分母都化为整数,正确的是( )
A、 B、 C、 D、
6、函数与在同一直角坐标系中的大致图像是( )
A B C D
7、一位经销商计划进一批运动鞋,他到学校对初二的100名男生的鞋号进行了调查,经销商最感兴趣的是这些鞋号的数据 ( )
A、中位数 B、平均数 C、方差 D、众位数
8、已知点(-1,y1)、(2,y2)、(π,y3)在双曲线 上,则下列关系正确的是 ( )
A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y13>y1>y2
9、在x轴上的点P的右侧有一点D,过点D作X轴的垂线交双曲线于点B,连接BO交AP于C,AP⊥X轴,设△AOC的面积为S1 ,梯形BCPD的面积为S2 ,则S1、S2的大小关系是( )
A、S1>S2 B、S110、如图,下边每个大正方形网格,都是由边长为1的小正方形组成,图中阴影部分面积最大的是 ( )
二、填空题 (每小题4分,共32分)
11、0.000 000 567用科学计数法表示为 。
12、某农业大学计划修建一块面积为2×106㎡的长方形实验田,该试验田的长y米与宽x米的函数解析式是 。
13、三角形的各边长分别是8、10、12、则连接各边中点所得的三角形的周长是 。
14、在Rt△ABC中,∠C=900 ,∠A=450 ,AB=10, BC= .
15、菱形两条对角线分别是8和6,则该菱形的高为 。
16、反比例函数图像的每一条曲线上,y都随着x的增大而增大,则,K的取值范围是 。
17、以正方形ABCD的BC为边作等边三角形BCE,点E在正方形内,则∠AED的度数为 。
18、如图,OABC是一张放在平面直角坐标系的矩形纸片,O上原点,点A在X轴的正半轴上,点C在Y轴的正半轴上,且OA=10,OC=8,在OC边上取一点D,沿AD翻折纸片,使O点落在BC边上的E点上,则点D的坐标为 。
三 计算 24分
19、计算 (7分)
20、解分式方程 (8分)
21、先化简代数式,再从-2、0、2中选一个数作为a的值求代数式的值 (9分)
四、推理论证 (每题10分,共30分)
22、如图,平行四边形ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,且,AE=CF,求证四边形BFDE是平行四边形。 (本题10分)
23、如图,等腰梯形ABCD,已知,AB∥CD,AD=BC, AB>CD,BD平分∠ABC,∠A=600 ,梯形的周长是20厘米,求CD的长和梯形的面积。
24、如图,菱形ABCD的对角线AC、BD交于点O,DE∥AC,CE∥BD, CD=OE。(本题10分)
五、应用题(第25题 10分,第26题 11分)
25、一辆汽车开往距离180千米的目的地,按原计划速度匀速行驶1小时后,以原速度的1.5倍匀速行驶到达目的地,比计划时间提前40分钟到达。原计划1小时多少公里?
26、如图是某校在四川省芦山地震捐款的统计情况,图1是各年级捐款人数占总捐款人数的百分比,图2是对部分学生捐款金额和人数的抽样调查,
(1)学校抽样调查的学生人数是多少?
(2)抽样数据的平均数、中位数、众数各是多少?
(3)若该校九年级共有400人捐款,请你估计全校捐款的总金额多少?
六、拓展与探究 (13分)
27、已知一次函数与X轴、Y轴分别相交于点D、C,和反比例函数相交于A、B两点,且点A(1,3),点B(3,m).求
(1)△AOB面积
(2)利用图像直接写出当x在什么取值范围时,
(3)动点P,从D点出发,以每秒1个单位长度向X轴的负方向移动,经过多长时间三角形ADP是直角三角形?
参考答案:
一、1—5 C、 B、 C、 D、 B 6—10 D、 D、 B、 C、 D
二、11、5.67×107 , 12、 , 13、15 , 14、 ,
15、4.8 , 16、K<1 , 17、1500 , 18、(0,5)
三、计算、
25、解,设原计划每小时行驶X公里,则方程为:
26、解:(1)16+12+10+8++4=50
(2)平均数:(5×4+10×8÷15×10+20×16+25×12)÷50=15.40(元)
中位数:20, 众位数:20
(3)全校捐款总人数:400÷(1-40%-35%)=1600 人
估计捐款总额:15.4×1600=14640 (元)
27、解:(1)把点A(1,3)代入,和得:
所以点B(3,1)、点C(0,4)、点D(4,0)
AOB的面积=S△COD-S△COA-S△BOD
=(4×4-3×1-1×3)÷2
=5
(2)、根据图像,当1(3)过点A作垂直于X轴,交X轴于,作垂直于直线CD,交X轴于,则:
因为C(0,4)、D(4,0)
所以∠CDO=450,,∠∠AP2P1=450
所以,AP1=DP1=P1P2=3
所以DP2=6
所以,当P点以每秒1个单位长度从点D向X轴的负半轴移动,在第3秒、第6秒时,三角形APD是一个直角三角形。
A B C D
19、解:
20、解:
经检验是原方程的根
21、解:
当a=2时,代数式的值为0
22、证明:因为四边形ABCD是平行四边形
所以 OA=OC,OB=OD
因为 AE=CF
所以 OE=OF
在△EOD和△FOB中:
OE=OF, OB=OD, ∠EOD=∠FOB
所以 △EOD≌△FOB
所以 ED=FB , EB=DF
所以四边形BFDE是平行四边形。
23、证明:过C作CE∥AD,交AB于E。
因为四边形ABCD是等腰梯形,
所以 四边形AECD是平行四边形,
所以 DC=AE,AD=EC=BC
所以∠CEB=∠A=60 ,
所以CE=BC=BE,
所以AD=AE=EB=BC=CD
因为梯形的周长为20㎝,
所以 CD=4㎝
过点D作DF⊥AB交AB于F.
DF=
梯形的面积为
24、证明:因为四边形ABCD是菱形,
所以 ∠DOC=900
因为DE∥AC,CE∥BD,
所以四边形CODE是矩形
CD=OE
八年级数学试卷
一、每题3分,共30分
1、甲、乙、丙三人进行射击测试,每人10次射击的平均成绩都是9.4环,方差分别是 , , ,在本次测试中成绩最稳定的是( )
A、甲 B、乙 C、丙 D、不确定
2、若一组数据33、28、27、、22、23的中位数是26,则数据中为( )
A、24 B、25 C、26 D、28
3、矩形的两条对角线夹角为600 ,对角线长为15厘米,则最短的边为( )
A、12㎝ B、10㎝ C、7.5㎝ D、5㎝
4、下列说法错误的是 ( )
A、对角线互相垂直的四边形是菱形;
B、对角线互相垂直平分且相等的四边形是正方形;
C、对角线相等的平行四边形是矩形;
D、一组对边平行,一组对角相等的四边形是平行四边形。
5、不改变分式的值,把分式的分子和分母都化为整数,正确的是( )
A、 B、 C、 D、
6、函数与在同一直角坐标系中的大致图像是( )
A B C D
7、一位经销商计划进一批运动鞋,他到学校对初二的100名男生的鞋号进行了调查,经销商最感兴趣的是这些鞋号的数据 ( )
A、中位数 B、平均数 C、方差 D、众位数
8、已知点(-1,y1)、(2,y2)、(π,y3)在双曲线 上,则下列关系正确的是 ( )
A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y13>y1>y2
9、在x轴上的点P的右侧有一点D,过点D作X轴的垂线交双曲线于点B,连接BO交AP于C,AP⊥X轴,设△AOC的面积为S1 ,梯形BCPD的面积为S2 ,则S1、S2的大小关系是( )
A、S1>S2 B、S1
二、填空题 (每小题4分,共32分)
11、0.000 000 567用科学计数法表示为 。
12、某农业大学计划修建一块面积为2×106㎡的长方形实验田,该试验田的长y米与宽x米的函数解析式是 。
13、三角形的各边长分别是8、10、12、则连接各边中点所得的三角形的周长是 。
14、在Rt△ABC中,∠C=900 ,∠A=450 ,AB=10, BC= .
15、菱形两条对角线分别是8和6,则该菱形的高为 。
16、反比例函数图像的每一条曲线上,y都随着x的增大而增大,则,K的取值范围是 。
17、以正方形ABCD的BC为边作等边三角形BCE,点E在正方形内,则∠AED的度数为 。
18、如图,OABC是一张放在平面直角坐标系的矩形纸片,O上原点,点A在X轴的正半轴上,点C在Y轴的正半轴上,且OA=10,OC=8,在OC边上取一点D,沿AD翻折纸片,使O点落在BC边上的E点上,则点D的坐标为 。
三 计算 24分
19、计算 (7分)
20、解分式方程 (8分)
21、先化简代数式,再从-2、0、2中选一个数作为a的值求代数式的值 (9分)
四、推理论证 (每题10分,共30分)
22、如图,平行四边形ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,且,AE=CF,求证四边形BFDE是平行四边形。 (本题10分)
23、如图,等腰梯形ABCD,已知,AB∥CD,AD=BC, AB>CD,BD平分∠ABC,∠A=600 ,梯形的周长是20厘米,求CD的长和梯形的面积。
24、如图,菱形ABCD的对角线AC、BD交于点O,DE∥AC,CE∥BD, CD=OE。(本题10分)
五、应用题(第25题 10分,第26题 11分)
25、一辆汽车开往距离180千米的目的地,按原计划速度匀速行驶1小时后,以原速度的1.5倍匀速行驶到达目的地,比计划时间提前40分钟到达。原计划1小时多少公里?
26、如图是某校在四川省芦山地震捐款的统计情况,图1是各年级捐款人数占总捐款人数的百分比,图2是对部分学生捐款金额和人数的抽样调查,
(1)学校抽样调查的学生人数是多少?
(2)抽样数据的平均数、中位数、众数各是多少?
(3)若该校九年级共有400人捐款,请你估计全校捐款的总金额多少?
六、拓展与探究 (13分)
27、已知一次函数与X轴、Y轴分别相交于点D、C,和反比例函数相交于A、B两点,且点A(1,3),点B(3,m).求
(1)△AOB面积
(2)利用图像直接写出当x在什么取值范围时,
(3)动点P,从D点出发,以每秒1个单位长度向X轴的负方向移动,经过多长时间三角形ADP是直角三角形?
参考答案:
一、1—5 C、 B、 C、 D、 B 6—10 D、 D、 B、 C、 D
二、11、5.67×107 , 12、 , 13、15 , 14、 ,
15、4.8 , 16、K<1 , 17、1500 , 18、(0,5)
三、计算、
25、解,设原计划每小时行驶X公里,则方程为:
26、解:(1)16+12+10+8++4=50
(2)平均数:(5×4+10×8÷15×10+20×16+25×12)÷50=15.40(元)
中位数:20, 众位数:20
(3)全校捐款总人数:400÷(1-40%-35%)=1600 人
估计捐款总额:15.4×1600=14640 (元)
27、解:(1)把点A(1,3)代入,和得:
所以点B(3,1)、点C(0,4)、点D(4,0)
AOB的面积=S△COD-S△COA-S△BOD
=(4×4-3×1-1×3)÷2
=5
(2)、根据图像,当1
因为C(0,4)、D(4,0)
所以∠CDO=450,,∠∠AP2P1=450
所以,AP1=DP1=P1P2=3
所以DP2=6
所以,当P点以每秒1个单位长度从点D向X轴的负半轴移动,在第3秒、第6秒时,三角形APD是一个直角三角形。
A B C D
19、解:
20、解:
经检验是原方程的根
21、解:
当a=2时,代数式的值为0
22、证明:因为四边形ABCD是平行四边形
所以 OA=OC,OB=OD
因为 AE=CF
所以 OE=OF
在△EOD和△FOB中:
OE=OF, OB=OD, ∠EOD=∠FOB
所以 △EOD≌△FOB
所以 ED=FB , EB=DF
所以四边形BFDE是平行四边形。
23、证明:过C作CE∥AD,交AB于E。
因为四边形ABCD是等腰梯形,
所以 四边形AECD是平行四边形,
所以 DC=AE,AD=EC=BC
所以∠CEB=∠A=60 ,
所以CE=BC=BE,
所以AD=AE=EB=BC=CD
因为梯形的周长为20㎝,
所以 CD=4㎝
过点D作DF⊥AB交AB于F.
DF=
梯形的面积为
24、证明:因为四边形ABCD是菱形,
所以 ∠DOC=900
因为DE∥AC,CE∥BD,
所以四边形CODE是矩形
CD=OE
同课章节目录
