探索三角形全等的条件(一)[上学期]
文档属性
| 名称 | 探索三角形全等的条件(一)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-24 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
洪家二中 陈捷
复习引入
探索发现
应用拓展
归纳小结
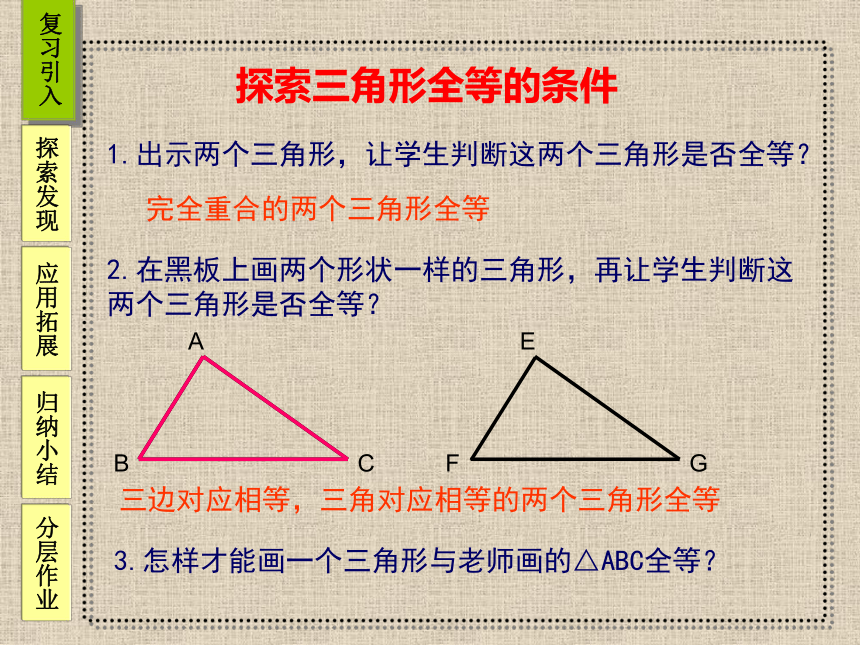
1.出示两个三角形,让学生判断这两个三角形是否全等?
2.在黑板上画两个形状一样的三角形,再让学生判断这两个三角形是否全等?
E
F
G
A
B
C
分层作业
3.怎样才能画一个三角形与老师画的△ABC全等?
探索三角形全等的条件
三边对应相等,三角对应相等的两个三角形全等
完全重合的两个三角形全等
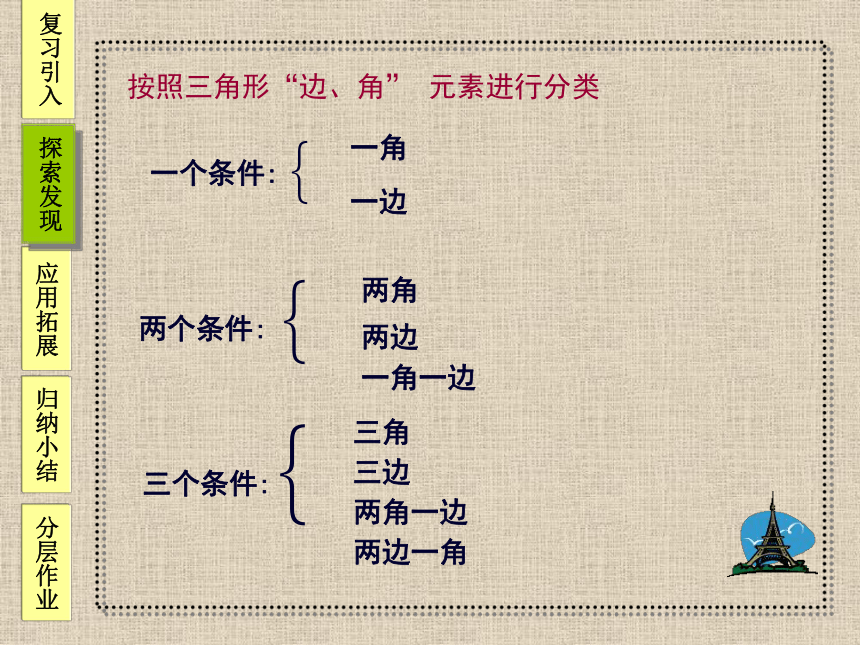
按照三角形“边、角” 元素进行分类
两个条件:
一角一边
两边
两角
{
一个条件:
{
一角
一边
三个条件:
两边一角
两角一边
三边
三角
{
应用拓展
归纳小结
分层作业
复习引入
探索发现
探索发现
应用拓展
复习引入
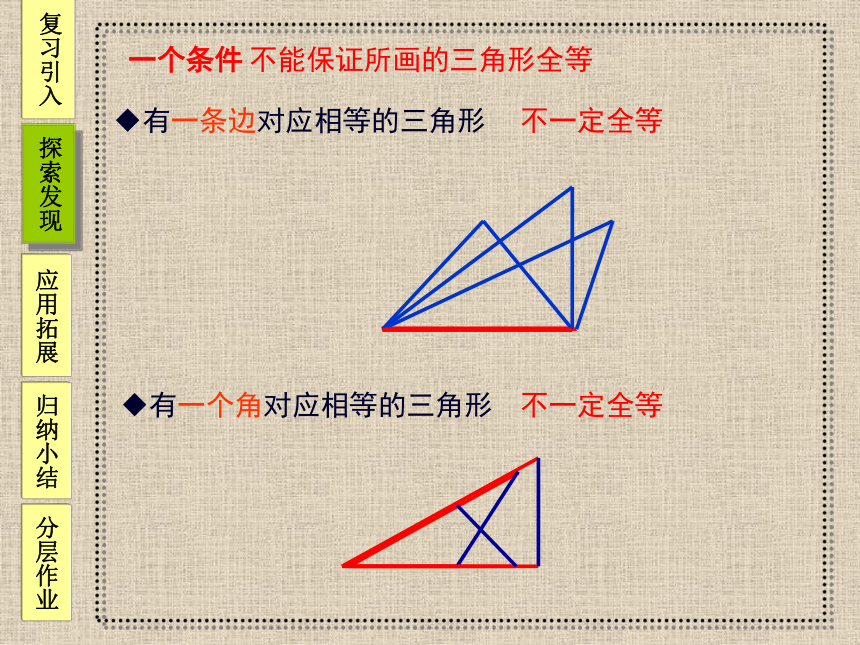
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
不能保证所画的三角形全等
归纳小结
分层作业
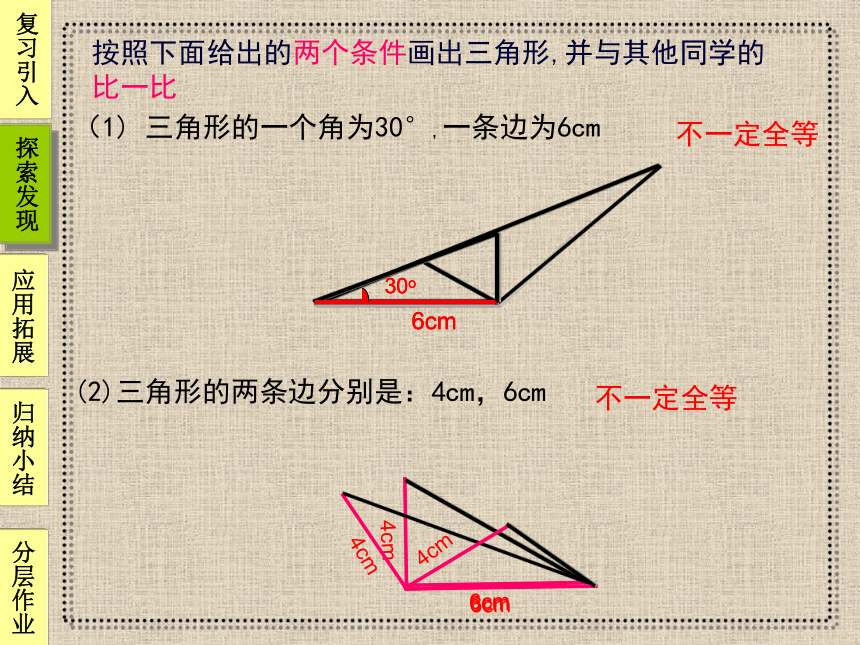
按照下面给出的两个条件画出三角形,并与其他同学的
比一比
(1) 三角形的一个角为30°,一条边为6cm
30o
6cm
30o
6cm
30o
6cm
不一定全等
(2)三角形的两条边分别是:4cm,6cm
4cm
6cm
4cm
6cm
复习引入
探索发现
应用拓展
归纳小结
分层作业
4cm
6cm
不一定全等
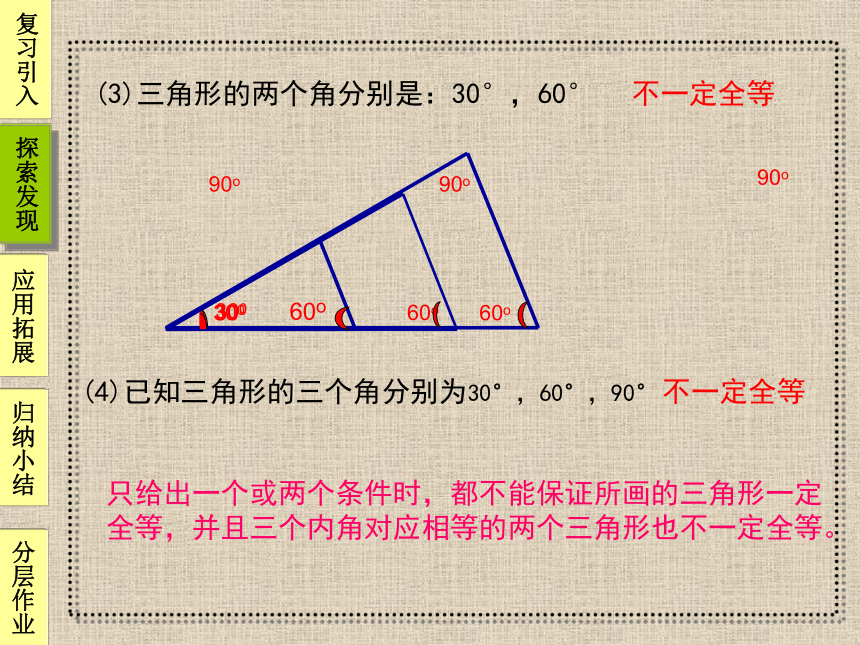
(3)三角形的两个角分别是:30°,60°
(4)已知三角形的三个角分别为30°,60°,90°
300
60o
300
60o
60o
300
不一定全等
90o
90o
90o
不一定全等
只给出一个或两个条件时,都不能保证所画的三角形一定
全等,并且三个内角对应相等的两个三角形也不一定全等。
复习引入
探索发现
应用拓展
归纳小结
分层作业
探索发现
应用拓展
归纳小结
复习引入
已知三角形三条边分别是4cm,5cm,7cm,画出这个三形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
分层作业
三个条件
三边对应相等的两个三角形全等,
或
简写为
边边边
SSS
探索发现
应用拓展
归纳小结
复习引入
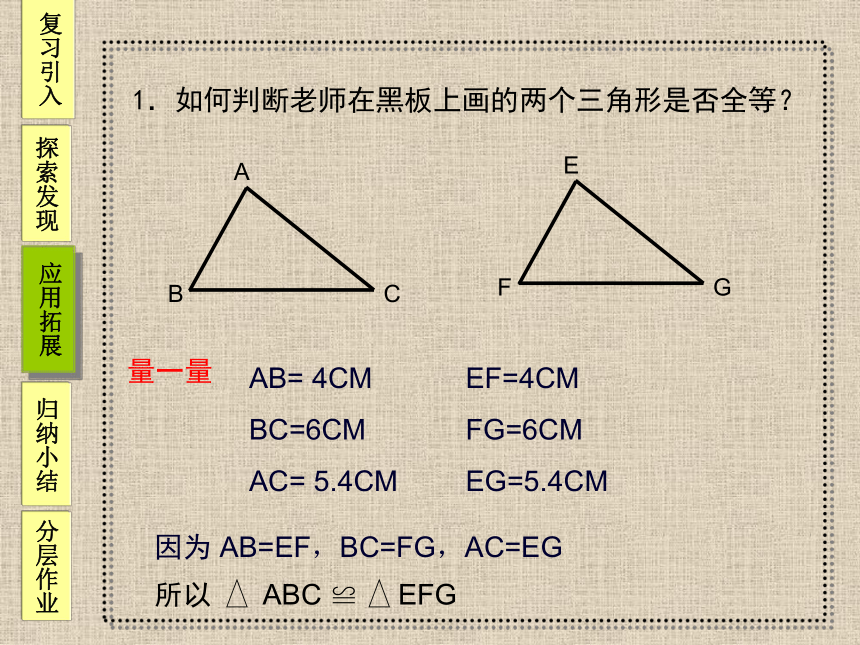
1.如何判断老师在黑板上画的两个三角形是否全等?
A
B
C
E
F
G
量一量
AB= 4CM
BC=6CM
AC= 5.4CM
EF=4CM
FG=6CM
EG=5.4CM
因为 AB=EF,BC=FG,AC=EG
所以
ABC ≌ EFG
分层作业
探索发现
应用拓展
归纳小结
复习引入
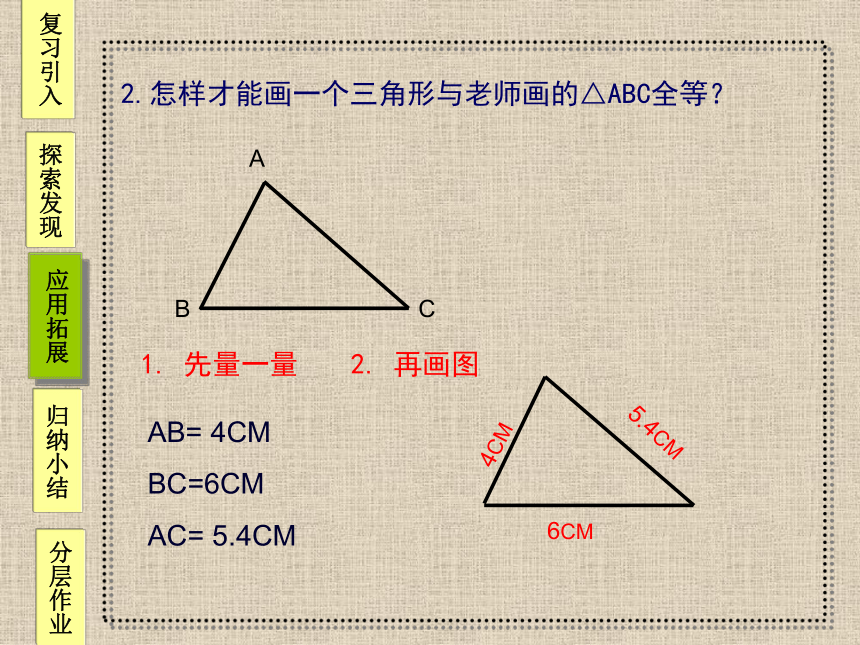
1. 先量一量
AB= 4CM
BC=6CM
AC= 5.4CM
2. 再画图
6CM
4CM
5.4CM
分层作业
A
B
C
2.怎样才能画一个三角形与老师画的△ABC全等?
探索发现
应用拓展
归纳小结
复习引入
BC
BC
分层作业
△DCB
BF=DC
或 BD=FC
A
B
C
D
3、填空题:
解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
=
△ABD ≌ ( )
S S S
(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
探索发现
应用拓展
归纳小结
复习引入
5.四边形ABCD中,AB=CD,AD=BC。△ABC和△CDA是否全等?∠A=∠C吗?说明理由。
(请同学们模仿题(1)做一做)
A
C
D
B
4.如图,AB=AC,BD=CD,H是BC的中点,指出图中全等三角形,它们全等的条件什么?
B H C
D
A
分层作业
探索发现
应用拓展
归纳小结
复习引入
做一做
取出课前自制长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。
发现什么?
三角形的大小和形状是固定不变的,而四边形
的形状会改变。
只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫
三角形的稳定性。
分层作业
探索发现
应用拓展
归纳小结
复习引入
四边形不具有稳定性,你能想出什么方法让它们的形状
不发生改变吗?
试一试
分层作业
探索发现
应用拓展
归纳小结
复习引入
请同学们谈谈本节课的收获与体会
本节课你学习了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题?
分层作业
必做题 :教科书 第140页 习题第2、3题
复习引入
探索发现
应用拓展
归纳小结
分层作业
选做题:1、想一想满足“两角一边或两边一角”
的条件能否判断两个三角形全等?
2、收集三角形的稳定性在日常生活中
应用的例子。
探索三角形全等的条件
条件1:边边边
(SSS)
三角形的稳定性
画图
练习
条件分类:
一个条件:一边,一角
两个条件:两边,两角
一边一角
三个条件:三边,三角
两边一角,
两角一边
洪家二中 陈捷
复习引入
探索发现
应用拓展
归纳小结
1.出示两个三角形,让学生判断这两个三角形是否全等?
2.在黑板上画两个形状一样的三角形,再让学生判断这两个三角形是否全等?
E
F
G
A
B
C
分层作业
3.怎样才能画一个三角形与老师画的△ABC全等?
探索三角形全等的条件
三边对应相等,三角对应相等的两个三角形全等
完全重合的两个三角形全等
按照三角形“边、角” 元素进行分类
两个条件:
一角一边
两边
两角
{
一个条件:
{
一角
一边
三个条件:
两边一角
两角一边
三边
三角
{
应用拓展
归纳小结
分层作业
复习引入
探索发现
探索发现
应用拓展
复习引入
一个条件
有一条边对应相等的三角形
不一定全等
有一个角对应相等的三角形
不一定全等
不能保证所画的三角形全等
归纳小结
分层作业
按照下面给出的两个条件画出三角形,并与其他同学的
比一比
(1) 三角形的一个角为30°,一条边为6cm
30o
6cm
30o
6cm
30o
6cm
不一定全等
(2)三角形的两条边分别是:4cm,6cm
4cm
6cm
4cm
6cm
复习引入
探索发现
应用拓展
归纳小结
分层作业
4cm
6cm
不一定全等
(3)三角形的两个角分别是:30°,60°
(4)已知三角形的三个角分别为30°,60°,90°
300
60o
300
60o
60o
300
不一定全等
90o
90o
90o
不一定全等
只给出一个或两个条件时,都不能保证所画的三角形一定
全等,并且三个内角对应相等的两个三角形也不一定全等。
复习引入
探索发现
应用拓展
归纳小结
分层作业
探索发现
应用拓展
归纳小结
复习引入
已知三角形三条边分别是4cm,5cm,7cm,画出这个三形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
分层作业
三个条件
三边对应相等的两个三角形全等,
或
简写为
边边边
SSS
探索发现
应用拓展
归纳小结
复习引入
1.如何判断老师在黑板上画的两个三角形是否全等?
A
B
C
E
F
G
量一量
AB= 4CM
BC=6CM
AC= 5.4CM
EF=4CM
FG=6CM
EG=5.4CM
因为 AB=EF,BC=FG,AC=EG
所以
ABC ≌ EFG
分层作业
探索发现
应用拓展
归纳小结
复习引入
1. 先量一量
AB= 4CM
BC=6CM
AC= 5.4CM
2. 再画图
6CM
4CM
5.4CM
分层作业
A
B
C
2.怎样才能画一个三角形与老师画的△ABC全等?
探索发现
应用拓展
归纳小结
复习引入
BC
BC
分层作业
△DCB
BF=DC
或 BD=FC
A
B
C
D
3、填空题:
解: △ABC≌△DCB
理由如下:
AB = CD
AC = BD
=
△ABD ≌ ( )
S S S
(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件
A
E
B D F C
探索发现
应用拓展
归纳小结
复习引入
5.四边形ABCD中,AB=CD,AD=BC。△ABC和△CDA是否全等?∠A=∠C吗?说明理由。
(请同学们模仿题(1)做一做)
A
C
D
B
4.如图,AB=AC,BD=CD,H是BC的中点,指出图中全等三角形,它们全等的条件什么?
B H C
D
A
分层作业
探索发现
应用拓展
归纳小结
复习引入
做一做
取出课前自制长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。
发现什么?
三角形的大小和形状是固定不变的,而四边形
的形状会改变。
只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫
三角形的稳定性。
分层作业
探索发现
应用拓展
归纳小结
复习引入
四边形不具有稳定性,你能想出什么方法让它们的形状
不发生改变吗?
试一试
分层作业
探索发现
应用拓展
归纳小结
复习引入
请同学们谈谈本节课的收获与体会
本节课你学习了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题?
分层作业
必做题 :教科书 第140页 习题第2、3题
复习引入
探索发现
应用拓展
归纳小结
分层作业
选做题:1、想一想满足“两角一边或两边一角”
的条件能否判断两个三角形全等?
2、收集三角形的稳定性在日常生活中
应用的例子。
探索三角形全等的条件
条件1:边边边
(SSS)
三角形的稳定性
画图
练习
条件分类:
一个条件:一边,一角
两个条件:两边,两角
一边一角
三个条件:三边,三角
两边一角,
两角一边
