第二章 轴对称单元检测题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第二单元综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共24分)
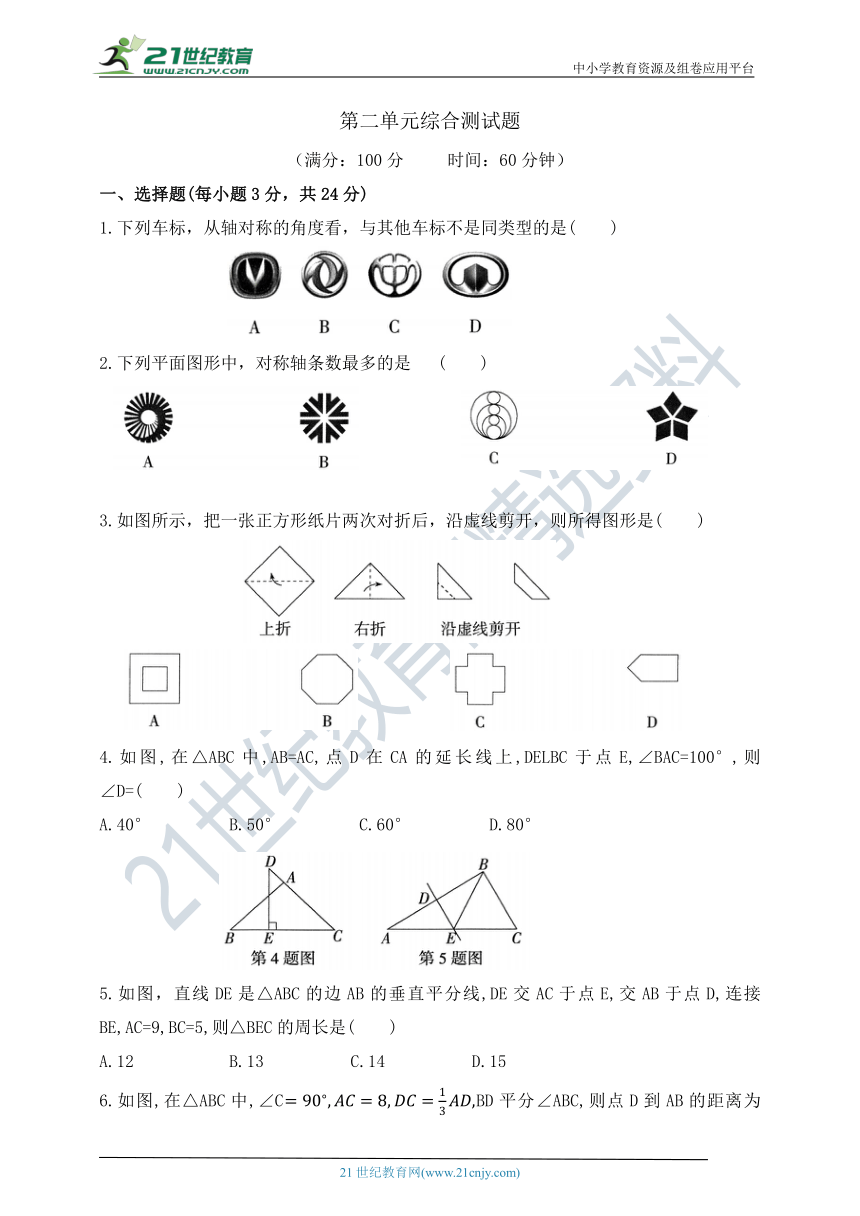
1.下列车标,从轴对称的角度看,与其他车标不是同类型的是( )
2.下列平面图形中,对称轴条数最多的是 ( )
3.如图所示,把一张正方形纸片两次对折后,沿虚线剪开,则所得图形是( )
4.如图,在△ABC中,AB=AC,点D在CA的延长线上,DELBC于点E,∠BAC=100°,则∠D=( )
A.40° B.50° C.60° D.80°
5.如图,直线DE是△ABC的边AB的垂直平分线,DE交AC于点E,交AB于点D,连接BE,AC=9,BC=5,则△BEC的周长是( )
A.12 B.13 C.14 D.15
6.如图,在△ABC中,∠CBD平分∠ABC,则点D到AB的距离为( )
A.4 B.3 C.2 D.1
7.如图所示,两个全等的等边三角形的边长为1m,一只电子蚂蚁由A点开始按A—B—
C—D—B—E—A沿等边三角形的边循环爬行,爬行2022m停下,则这只电子蚂蚁停在( )
A.点A处 B.点B处 C.点C处 D.点E处
8.如图,△ABC是等边三角形,AD=AE,BD=CE,则∠ACE的度数是( )
A.40° B.50° C.60° D.70°
二、填空题(每小题4分,共24分)
9.在角、线段、等边三角形中,对称轴最多的是__________,它有________条对称轴;对称轴最少的是__________,它有__________条对称轴.
10.观察下列各组图形(如图所示),其中成轴对称的是___________.(填写序号)
11.如图,三角形纸片ABC中,∠ACB=90°,在BC边上取一点P,沿AP所在直线折叠,点B落在AC的延长线上的点D处,∠CPD=40°,则∠PAC=___________°.
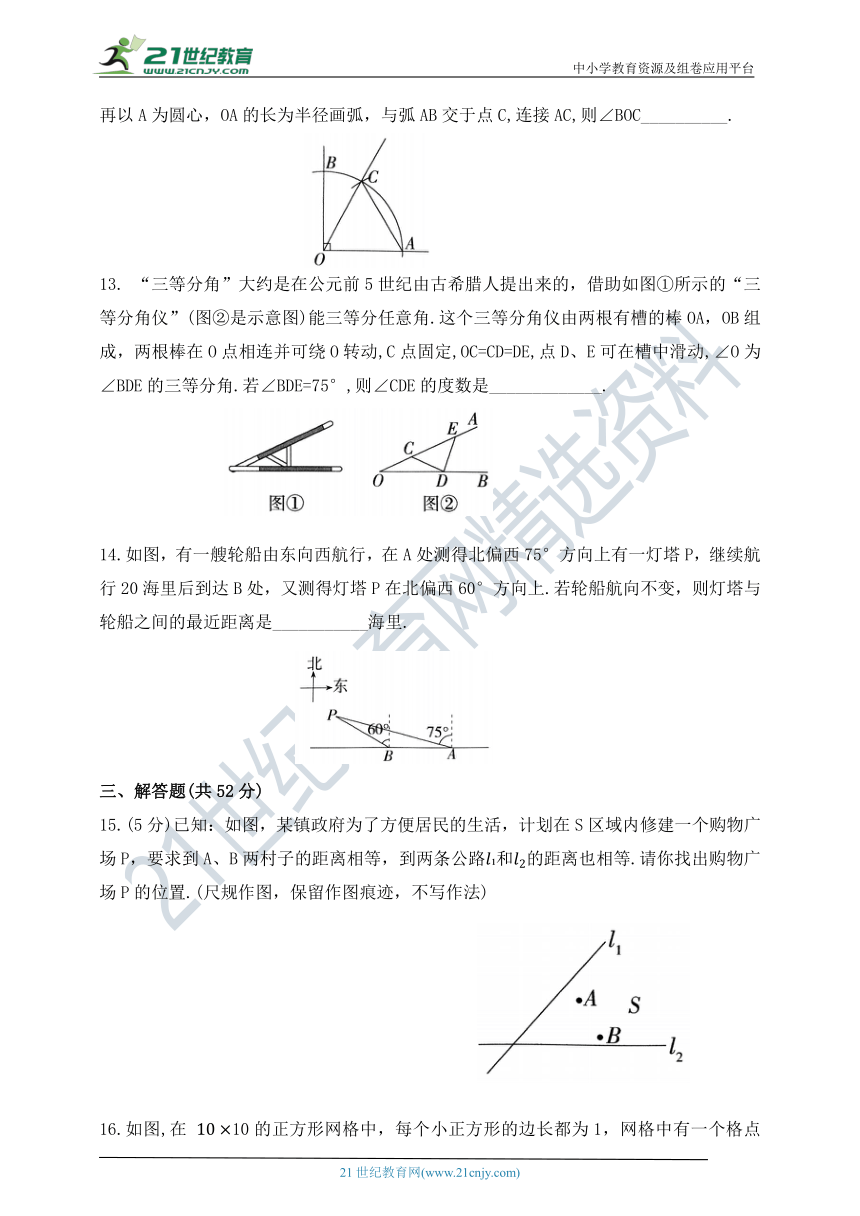
12.如图,用圆规以直角顶点0为圆心,以适当长为半径画弧,交两直角边于A、B两点,再以A为圆心,OA的长为半径画弧,与弧AB交于点C,连接AC,则∠BOC__________.
13. “三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图①所示的“三等分角仪”(图②是示意图)能三等分任意角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,∠O为∠BDE的三等分角.若∠BDE=75°,则∠CDE的度数是_____________.
14.如图,有一艘轮船由东向西航行,在A处测得北偏西75°方向上有一灯塔P,继续航行20海里后到达B处,又测得灯塔P在北偏西60°方向上.若轮船航向不变,则灯塔与轮船之间的最近距离是___________海里.
三、解答题(共52分)
15.(5分)已知:如图,某镇政府为了方便居民的生活,计划在S区域内修建一个购物广场P,要求到A、B两村子的距离相等,到两条公路 和的距离也相等.请你找出购物广场P的位置.(尺规作图,保留作图痕迹,不写作法)
16.如图,在 10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△ABC关于直线对称的△A B C ;(要求:A与A ,B与 C与C 相对应)
(2)求出△A B C 的面积;
(3)在直线上找一点P,使得 的值最小.
17. (7分)如图,四边形ABCD中,AB∥CD,点E为CD上一点,BE、AE分别平分∠ABC、∠BAD.求证:CD=AD+BC.
18. (7分)如图,在△中, AD平分 交BC于点D,BD: 求点D到AB的距离.
19. (8分)如图,在Rt△ABC中, AC的垂直平分线DE交AB于点D,交AC于点E,连接CD.
(1)求 的度数;
(2)若 ,求AB的长.
20.(8分)用两个全等的三角形可以拼出各种不同的图形.已画出其中一个三角形(如图),请你分别补画出另一个与其全等的三角形,使每个图形分别成为不同的轴对称图形,并画出各图形的一条对称轴(所画三角形可与原三角形有重叠的部分,至少设计四种).
21.(10分)已知:如图, 点D是BC的中点,AB平分 垂足为E.
(1)求证:
(2)若 ∥试判断 的形状,并说明理由.
参考答案
1.B 只有B不是轴对称图形.选项A、C、D都是轴对称图形,且都只有一条对称轴.
2.B 选项A中的图形没有对称轴,选项B中的图形有8条对称轴,选项C中的图形有1条对称轴,选项D中的图形有5条对称轴,故选B.
3.A 按照题中的顺序动手操作,可知选A.
4.B ∵AB=AC,∠BAC=100°,∴∠C=∠B=40°,∵DE⊥BC于点E, 故选B.
5.C 因为直线DE是线段AB的垂直平分线,所以EA=EB,所以 的周长 BC+CE+EA=BC+AC=14,故选C.
6.C 如图,过点D作 于E,
因为 所以
因为BD平分 所以DE=CD=2,
故点D到AB的距离为2.故选C.
7.A 由题意得电子蚂蚁爬行6m为一个循环组,因为2022÷6=337,
所以电子蚂蚁爬行2022m停在点A处,故选A.
8.C∵△ABC是等边三角形,∴AB=AC=BC,∠B=60°,
在△ABD和△ACE中, △ACE,∴∠ACE=∠B=60°,故选C.
9.答案 等边三角形;3;角;1
解析 等边三角形有3条对称轴,分别是三边的中线所在的直线;角只有一条对称轴,是角平分线所在的直线;线段有两条对称轴,分别是线段的垂直平分线和线段本身所在的直线.
10.答案 ②
解析 找成轴对称的图形的关键是寻找对称轴,成轴对称的两个图形沿对称轴折叠后可完全重合.
11.答案 20
解析 由题意可知∠D=∠B,∠DAP=∠BAP=
12.答案
解析 由题意可知 所以△AOC是等边三角形,所以∠AOC=60°,所以∠BOC=90°-∠AOC=30°.
13.答案
解析 由题意知3∠O=∠BDE=75°,∴∠O=
14.答案 10
解析 如图,过P作 交直线AB于D,则PD的长就是灯塔与轮船之间的最近距离,∠PDB=90°,∵∠PBD=90°-60°=30°,∴∠PBA=150°, 20(海里),在 中, 海里,∠PBD=30°, (海里).
15.解析 如图所示,点P即为所求.
16.解析 (1)如图所示,△即为所求.
(2)△A B C 的面积 ×1×4=5.
(3)如图,点P即为所求.
17.证明∵AE平分∠DAB,BE平分
∥∴CD
18.解析 如图,过点D作DELAB于E.
∵AD平分
∵BD
∴DE=2.6cm,∴点D到AB的距离为2.6cm.
19.解析 (1)∵DE垂直平分AC,∴ ∴
CD=
,∴BD
∠A=30°,∴AD=2DE=6,∴AB=2AD=12.
20.解析 如图所示(答案不唯一).
21.解析 (1)证明:∵AB=AC,点D是BC的中点,∴AD⊥BC,∴∠ADB=90°,
∵BE⊥AE,∴∠E=90°,∴∠E=∠ADB,
∵AB平分∠DAE,∴∠DAB=∠EAB,
在△ADB和△AEB中, ∴△ADB≌△AEB(AAS),
是等边三角形.
理由:∵BE∥AC,∠E=90°,
点D是BC的中点,
由(1)知∠EAB=∠BAD,
∴∠BAC=∠BAD+∠DAC=60°,∴△ABC是等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元综合测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共24分)
1.下列车标,从轴对称的角度看,与其他车标不是同类型的是( )
2.下列平面图形中,对称轴条数最多的是 ( )
3.如图所示,把一张正方形纸片两次对折后,沿虚线剪开,则所得图形是( )
4.如图,在△ABC中,AB=AC,点D在CA的延长线上,DELBC于点E,∠BAC=100°,则∠D=( )
A.40° B.50° C.60° D.80°
5.如图,直线DE是△ABC的边AB的垂直平分线,DE交AC于点E,交AB于点D,连接BE,AC=9,BC=5,则△BEC的周长是( )
A.12 B.13 C.14 D.15
6.如图,在△ABC中,∠CBD平分∠ABC,则点D到AB的距离为( )
A.4 B.3 C.2 D.1
7.如图所示,两个全等的等边三角形的边长为1m,一只电子蚂蚁由A点开始按A—B—
C—D—B—E—A沿等边三角形的边循环爬行,爬行2022m停下,则这只电子蚂蚁停在( )
A.点A处 B.点B处 C.点C处 D.点E处
8.如图,△ABC是等边三角形,AD=AE,BD=CE,则∠ACE的度数是( )
A.40° B.50° C.60° D.70°
二、填空题(每小题4分,共24分)
9.在角、线段、等边三角形中,对称轴最多的是__________,它有________条对称轴;对称轴最少的是__________,它有__________条对称轴.
10.观察下列各组图形(如图所示),其中成轴对称的是___________.(填写序号)
11.如图,三角形纸片ABC中,∠ACB=90°,在BC边上取一点P,沿AP所在直线折叠,点B落在AC的延长线上的点D处,∠CPD=40°,则∠PAC=___________°.
12.如图,用圆规以直角顶点0为圆心,以适当长为半径画弧,交两直角边于A、B两点,再以A为圆心,OA的长为半径画弧,与弧AB交于点C,连接AC,则∠BOC__________.
13. “三等分角”大约是在公元前5世纪由古希腊人提出来的,借助如图①所示的“三等分角仪”(图②是示意图)能三等分任意角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动,∠O为∠BDE的三等分角.若∠BDE=75°,则∠CDE的度数是_____________.
14.如图,有一艘轮船由东向西航行,在A处测得北偏西75°方向上有一灯塔P,继续航行20海里后到达B处,又测得灯塔P在北偏西60°方向上.若轮船航向不变,则灯塔与轮船之间的最近距离是___________海里.
三、解答题(共52分)
15.(5分)已知:如图,某镇政府为了方便居民的生活,计划在S区域内修建一个购物广场P,要求到A、B两村子的距离相等,到两条公路 和的距离也相等.请你找出购物广场P的位置.(尺规作图,保留作图痕迹,不写作法)
16.如图,在 10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△ABC关于直线对称的△A B C ;(要求:A与A ,B与 C与C 相对应)
(2)求出△A B C 的面积;
(3)在直线上找一点P,使得 的值最小.
17. (7分)如图,四边形ABCD中,AB∥CD,点E为CD上一点,BE、AE分别平分∠ABC、∠BAD.求证:CD=AD+BC.
18. (7分)如图,在△中, AD平分 交BC于点D,BD: 求点D到AB的距离.
19. (8分)如图,在Rt△ABC中, AC的垂直平分线DE交AB于点D,交AC于点E,连接CD.
(1)求 的度数;
(2)若 ,求AB的长.
20.(8分)用两个全等的三角形可以拼出各种不同的图形.已画出其中一个三角形(如图),请你分别补画出另一个与其全等的三角形,使每个图形分别成为不同的轴对称图形,并画出各图形的一条对称轴(所画三角形可与原三角形有重叠的部分,至少设计四种).
21.(10分)已知:如图, 点D是BC的中点,AB平分 垂足为E.
(1)求证:
(2)若 ∥试判断 的形状,并说明理由.
参考答案
1.B 只有B不是轴对称图形.选项A、C、D都是轴对称图形,且都只有一条对称轴.
2.B 选项A中的图形没有对称轴,选项B中的图形有8条对称轴,选项C中的图形有1条对称轴,选项D中的图形有5条对称轴,故选B.
3.A 按照题中的顺序动手操作,可知选A.
4.B ∵AB=AC,∠BAC=100°,∴∠C=∠B=40°,∵DE⊥BC于点E, 故选B.
5.C 因为直线DE是线段AB的垂直平分线,所以EA=EB,所以 的周长 BC+CE+EA=BC+AC=14,故选C.
6.C 如图,过点D作 于E,
因为 所以
因为BD平分 所以DE=CD=2,
故点D到AB的距离为2.故选C.
7.A 由题意得电子蚂蚁爬行6m为一个循环组,因为2022÷6=337,
所以电子蚂蚁爬行2022m停在点A处,故选A.
8.C∵△ABC是等边三角形,∴AB=AC=BC,∠B=60°,
在△ABD和△ACE中, △ACE,∴∠ACE=∠B=60°,故选C.
9.答案 等边三角形;3;角;1
解析 等边三角形有3条对称轴,分别是三边的中线所在的直线;角只有一条对称轴,是角平分线所在的直线;线段有两条对称轴,分别是线段的垂直平分线和线段本身所在的直线.
10.答案 ②
解析 找成轴对称的图形的关键是寻找对称轴,成轴对称的两个图形沿对称轴折叠后可完全重合.
11.答案 20
解析 由题意可知∠D=∠B,∠DAP=∠BAP=
12.答案
解析 由题意可知 所以△AOC是等边三角形,所以∠AOC=60°,所以∠BOC=90°-∠AOC=30°.
13.答案
解析 由题意知3∠O=∠BDE=75°,∴∠O=
14.答案 10
解析 如图,过P作 交直线AB于D,则PD的长就是灯塔与轮船之间的最近距离,∠PDB=90°,∵∠PBD=90°-60°=30°,∴∠PBA=150°, 20(海里),在 中, 海里,∠PBD=30°, (海里).
15.解析 如图所示,点P即为所求.
16.解析 (1)如图所示,△即为所求.
(2)△A B C 的面积 ×1×4=5.
(3)如图,点P即为所求.
17.证明∵AE平分∠DAB,BE平分
∥∴CD
18.解析 如图,过点D作DELAB于E.
∵AD平分
∵BD
∴DE=2.6cm,∴点D到AB的距离为2.6cm.
19.解析 (1)∵DE垂直平分AC,∴ ∴
CD=
,∴BD
∠A=30°,∴AD=2DE=6,∴AB=2AD=12.
20.解析 如图所示(答案不唯一).
21.解析 (1)证明:∵AB=AC,点D是BC的中点,∴AD⊥BC,∴∠ADB=90°,
∵BE⊥AE,∴∠E=90°,∴∠E=∠ADB,
∵AB平分∠DAE,∴∠DAB=∠EAB,
在△ADB和△AEB中, ∴△ADB≌△AEB(AAS),
是等边三角形.
理由:∵BE∥AC,∠E=90°,
点D是BC的中点,
由(1)知∠EAB=∠BAD,
∴∠BAC=∠BAD+∠DAC=60°,∴△ABC是等边三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
