13.2.1 探索三角形全等的条件SSS[上学期]
文档属性
| 名称 | 13.2.1 探索三角形全等的条件SSS[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 483.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-16 00:00:00 | ||
图片预览



文档简介
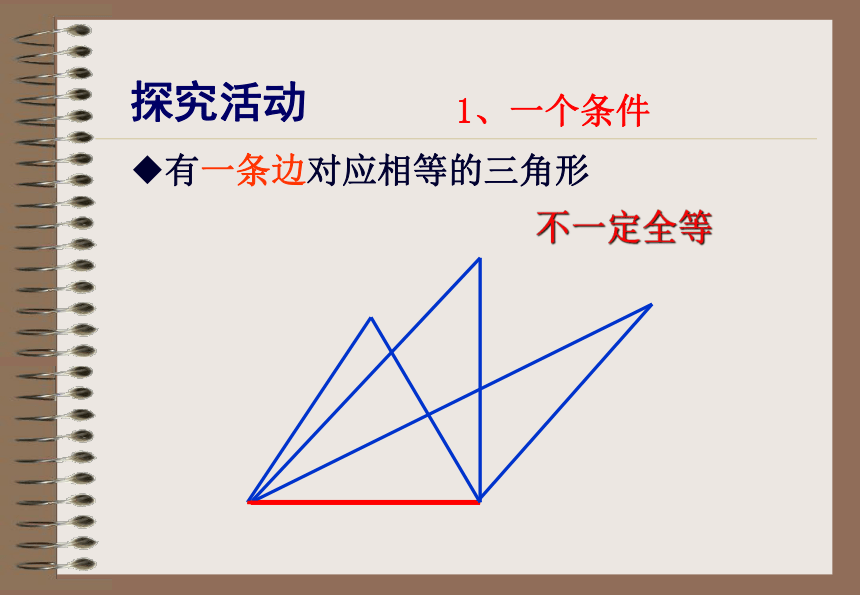
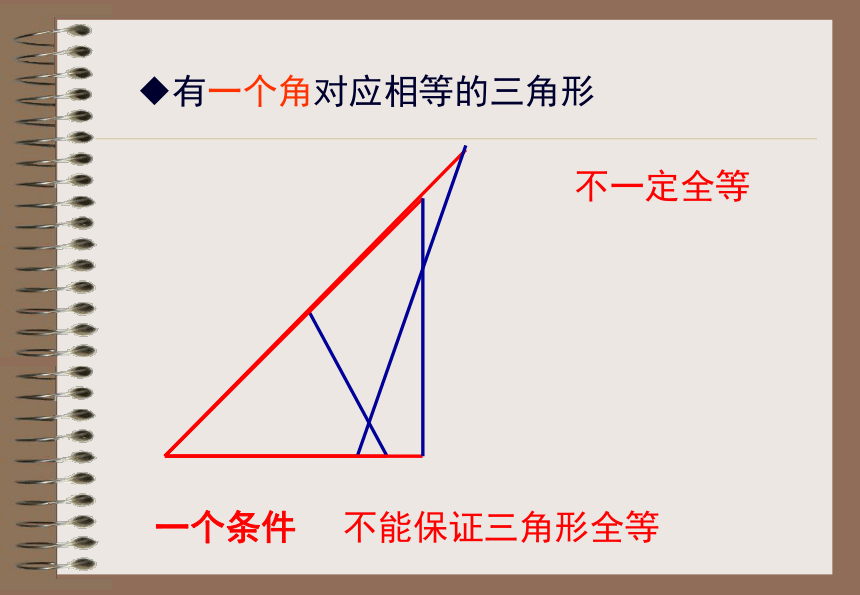
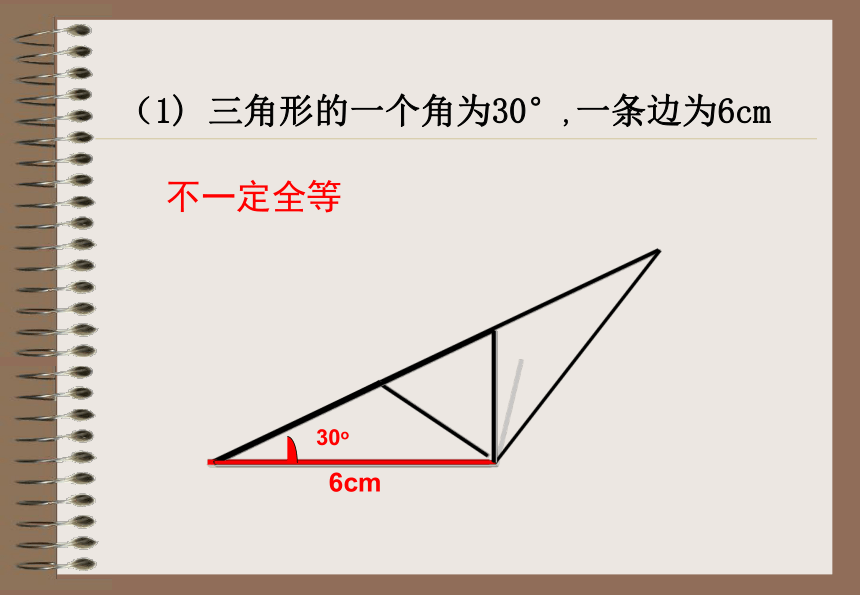
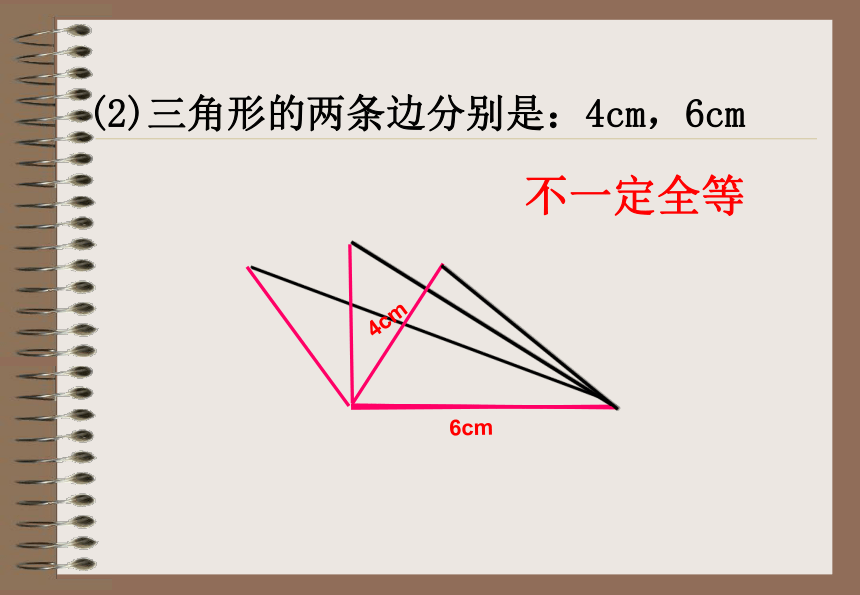
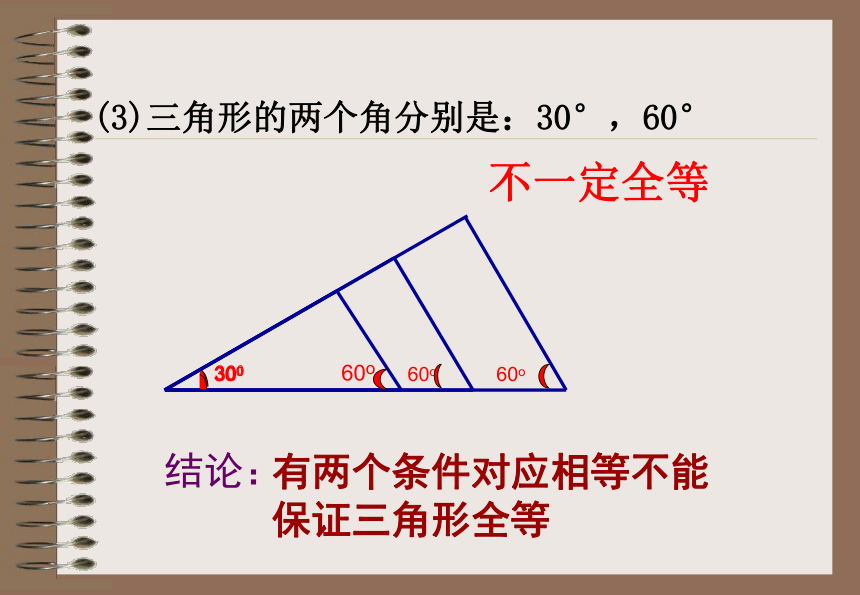
课件23张PPT。探索三角形全等的条件授课人:李萍萍情境问题: 小明家的衣橱上有两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明到玻璃店配一块回来,聪明的同学,小明该测量哪些数据呢?数据能尽可能少吗? 1、一个条件有一条边对应相等的三角形不一定全等探究活动有一个角对应相等的三角形不一定全等 一个条件不能保证三角形全等2、按照下面给出的两个条件画出三角形,并将完成的三角形比一比(1)三角形的一个角为 30°,一条边为6cm ;探究活动(2)三角形的两条边分别是 4cm 和 6cm ;(3)三角形的两个角分别是 30°和 60°.(1) 三角形的一个角为30°,一条边为6cm不一定全等(2)三角形的两条边分别是:4cm,6cm不一定全等(3)三角形的两个角分别是:30°,60°不一定全等结论:有两个条件对应相等不能
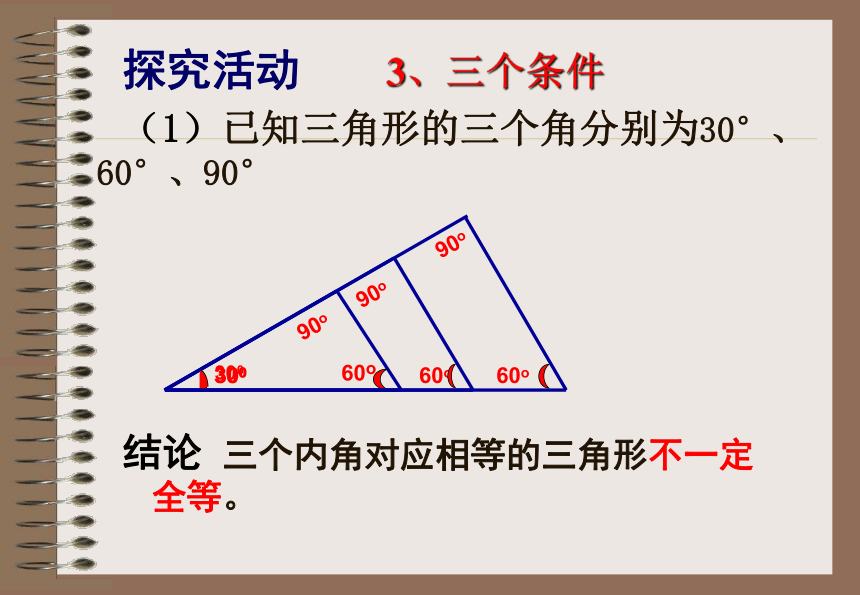
保证三角形全等 (1)已知三角形的三个角分别为30°、60°、90° 三个内角对应相等的三角形不一定全等。探究活动3、三个条件结论 2、已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?三边对应相等的两个三角形全等,探究新知边边边公理 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S ——边AB=EFBC=FGAC=EG(SSS)规范书写:∴∵议一议:已知: 如图,AC=AD ,BC=BD 请说明△ACB ≌ △ADB的理由.
ABCD说明:
△ACB ≌ △ADB
这两个条件够吗?已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?还要一条边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB
又是△ADB的一条边
△ACB 和△ADB的
公共边议一议:例题1 如图, △ABC 是一个钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD ACDB证明:在△ABD 和△ACD中AB = AC ∴ △ABD ≌ △ACD(已知)(公共边)(已知)AD = ADDB = DC( SSS )动 态 演 示P96思考:图3已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD(等式性质)
即AB=FD
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已证)
AB=FD(已知)
∴△ABC≌△FDE(SSS)若求证∠C=∠E ,如何证明?分析:要证明ABC≌△FDE ,有已知 条件AC=FE,BC=DE 两对边
还要一对边 AB=FDP96思考:问:
动 态 演 示变式1练习:已知:如图2,点A、B、C、D在同一条直线上,AC=DB,AE=DF,BE=CF图2求证:(1)△EAB≌△FDC、(2)DF= AE课堂小结1.边边边公理:有三边对应相等的两个三角形全等 简写成“边边边”(SSS)2.边边边公理的发现过程所用到的数学方法(包括画 图、猜想、分析、归纳等.)3.边边边公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.转化1. 说明两个三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中. 用结论说明两个三角形全等需注意知识的升华1.P103 作业题1,2题.
(做在作业本上)
2.预习下一节的内容并在课本上完成课后练习。
再 见努力学习吧,有了知识的浇灌,
某一天你也会成为参天大树!
保证三角形全等 (1)已知三角形的三个角分别为30°、60°、90° 三个内角对应相等的三角形不一定全等。探究活动3、三个条件结论 2、已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?三边对应相等的两个三角形全等,探究新知边边边公理 有三边对应相等的两个三角形全等.
可以简写成 “边边边” 或“ SSS ” S ——边AB=EFBC=FGAC=EG(SSS)规范书写:∴∵议一议:已知: 如图,AC=AD ,BC=BD 请说明△ACB ≌ △ADB的理由.
ABCD说明:
△ACB ≌ △ADB
这两个条件够吗?已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD说明:
△ACB ≌ △ADB.
这两个条件够吗?
还要什么条件呢?还要一条边议一议:已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
ABCD它既是△ACB的一条边,看看线段AB
又是△ADB的一条边
△ACB 和△ADB的
公共边议一议:例题1 如图, △ABC 是一个钢架,AB = AC ,AD是
连结点A与BC中点D的支架.
求证: △ABD ≌ △ACD ACDB证明:在△ABD 和△ACD中AB = AC ∴ △ABD ≌ △ACD(已知)(公共边)(已知)AD = ADDB = DC( SSS )动 态 演 示P96思考:图3已知:如图1 ,AC=FE,AD=FB,BC=DE
求证:ABC≌△FDE 证明:∵ AD=FB
∴AD+DB=FB+BD(等式性质)
即AB=FD
在△ABC和△FDE 中AC=FE(已知)
BC=DE(已证)
AB=FD(已知)
∴△ABC≌△FDE(SSS)若求证∠C=∠E ,如何证明?分析:要证明ABC≌△FDE ,有已知 条件AC=FE,BC=DE 两对边
还要一对边 AB=FDP96思考:问:
动 态 演 示变式1练习:已知:如图2,点A、B、C、D在同一条直线上,AC=DB,AE=DF,BE=CF图2求证:(1)△EAB≌△FDC、(2)DF= AE课堂小结1.边边边公理:有三边对应相等的两个三角形全等 简写成“边边边”(SSS)2.边边边公理的发现过程所用到的数学方法(包括画 图、猜想、分析、归纳等.)3.边边边公理的应用中所用到的数学方法:
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.转化1. 说明两个三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中. 用结论说明两个三角形全等需注意知识的升华1.P103 作业题1,2题.
(做在作业本上)
2.预习下一节的内容并在课本上完成课后练习。
再 见努力学习吧,有了知识的浇灌,
某一天你也会成为参天大树!
