三角形全等的条件[上学期]
文档属性
| 名称 | 三角形全等的条件[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 494.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-18 00:00:00 | ||
图片预览







文档简介
课件23张PPT。三角形全等的条件如图,小明不慎将一块三角形模具打碎为两块,他是否可以
只带其中的一块碎片到商店去,就能配一块与原来一样的
三角形模具吗? 如果可以,带哪块去合适?
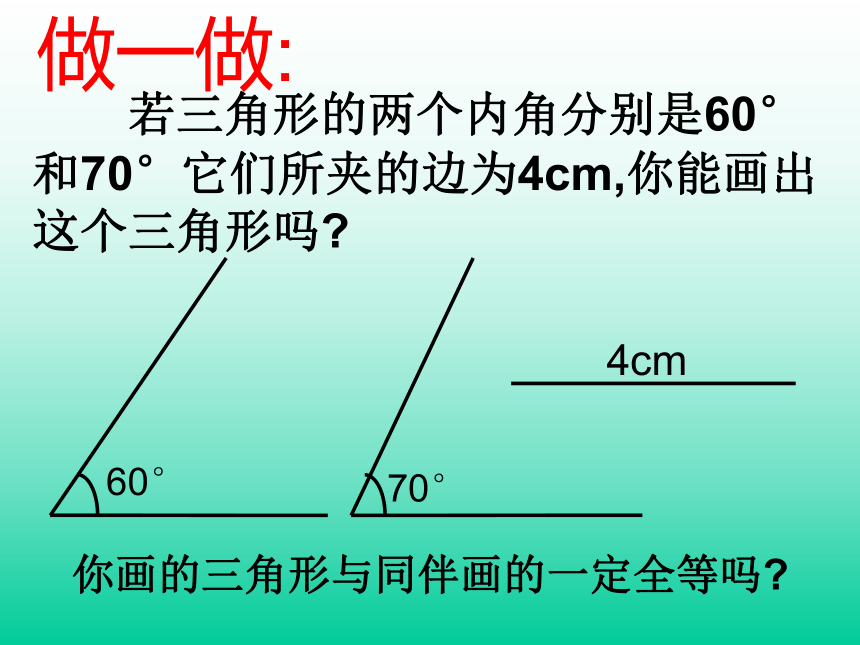
你能说明其中理由吗?想一想怎么办?可以帮帮我吗?做一做: 若三角形的两个内角分别是60°和70°它们所夹的边为4cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗? 先任意画出一个△ABC,
再画一个△A/B/C/,使A/B/=AB,
∠A/ =∠A, ∠B/ =∠B 。把画好
的△A/B/C/剪下,放到△ABC上,
它们全等吗?探究1已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B :画法:1、画A/ B/ =AB △A/B/C/就是所要画的三角形。问:通过实验可以发现什么事实?2、在A/ B/的同旁画∠ DA/ B/ =∠A ,
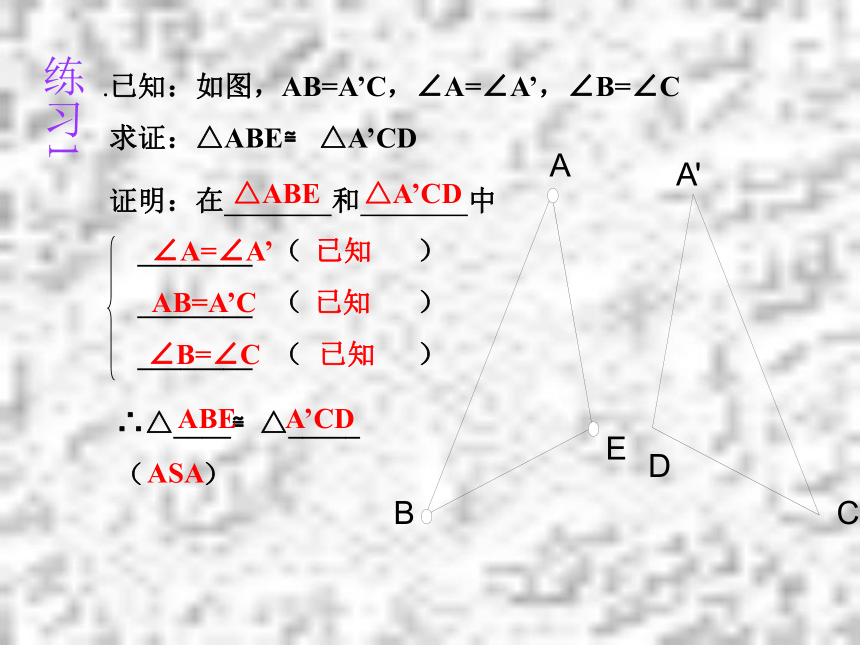
∠E B/ A/ =∠B, A/ D, B/ E交于点C/ 。 有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。探究反映的规律是:到目前为此,我们共学了几种判定三角形全等的方法?1、边边边(SSS)3、角边角(ASA)4、角角边(AAS)2、边角边(SAS).已知:如图,AB=A’C,∠A=∠A’,∠B=∠C
求证:△ABE≌ △A’CD 练习1∠A=∠A’ 已知
AB=A’C 已知
∠B=∠C 已知ABE A’CD△ABE △A’CDASA例题讲解:巩固练习1.如图,∠1=∠2,∠3=∠4
求证:AC=ADABD
ABC
ABD ABC
∠1=∠2 已知
AB=AB
∠ABD=∠ABC 已知
ABD ABC ASA
AC=ADAO=BO(1)学习了角边角。
(2)由实践证明角边角是真命题。
(3)注意角边角中两角夹边的条件。小结 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?探究2有两个角和其中一个角的对边对应相等的两个三角形全等
(简写成“角角边”或“AAS”)。巩固练习1.如图,∠1=∠2,∠3=∠4
求证:AC=AD2.已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
证明:评价1.错例辨析
若△ABC的∠B=∠C,△A’B’C’的∠B’=∠C’,且BC=B’C’,
那么△ABC与△A’B’C’全等吗?为什么?1212(3)如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC知识应用1.如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?布置作业P104 习题13.2 5、 6、 11、12.
只带其中的一块碎片到商店去,就能配一块与原来一样的
三角形模具吗? 如果可以,带哪块去合适?
你能说明其中理由吗?想一想怎么办?可以帮帮我吗?做一做: 若三角形的两个内角分别是60°和70°它们所夹的边为4cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗? 先任意画出一个△ABC,
再画一个△A/B/C/,使A/B/=AB,
∠A/ =∠A, ∠B/ =∠B 。把画好
的△A/B/C/剪下,放到△ABC上,
它们全等吗?探究1已知:任意 △ ABC,画一个△ A/B/C/,
使A/B/=AB, ∠A/ =∠A, ∠B/ =∠B :画法:1、画A/ B/ =AB △A/B/C/就是所要画的三角形。问:通过实验可以发现什么事实?2、在A/ B/的同旁画∠ DA/ B/ =∠A ,
∠E B/ A/ =∠B, A/ D, B/ E交于点C/ 。 有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。探究反映的规律是:到目前为此,我们共学了几种判定三角形全等的方法?1、边边边(SSS)3、角边角(ASA)4、角角边(AAS)2、边角边(SAS).已知:如图,AB=A’C,∠A=∠A’,∠B=∠C
求证:△ABE≌ △A’CD 练习1∠A=∠A’ 已知
AB=A’C 已知
∠B=∠C 已知ABE A’CD△ABE △A’CDASA例题讲解:巩固练习1.如图,∠1=∠2,∠3=∠4
求证:AC=ADABD
ABC
ABD ABC
∠1=∠2 已知
AB=AB
∠ABD=∠ABC 已知
ABD ABC ASA
AC=ADAO=BO(1)学习了角边角。
(2)由实践证明角边角是真命题。
(3)注意角边角中两角夹边的条件。小结 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?探究2有两个角和其中一个角的对边对应相等的两个三角形全等
(简写成“角角边”或“AAS”)。巩固练习1.如图,∠1=∠2,∠3=∠4
求证:AC=AD2.已知,如图,∠1=∠2,∠C=∠D
求证:AC=AD
证明:评价1.错例辨析
若△ABC的∠B=∠C,△A’B’C’的∠B’=∠C’,且BC=B’C’,
那么△ABC与△A’B’C’全等吗?为什么?1212(3)如图,已知∠1=∠2,∠3=∠4,BD=CE
求证:AB=AC知识应用1.如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?布置作业P104 习题13.2 5、 6、 11、12.
