11.2三角形全等的判定(SAS)[上学期]
文档属性
| 名称 | 11.2三角形全等的判定(SAS)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-08 00:00:00 | ||
图片预览







文档简介
课件31张PPT。13.2 全等条件2
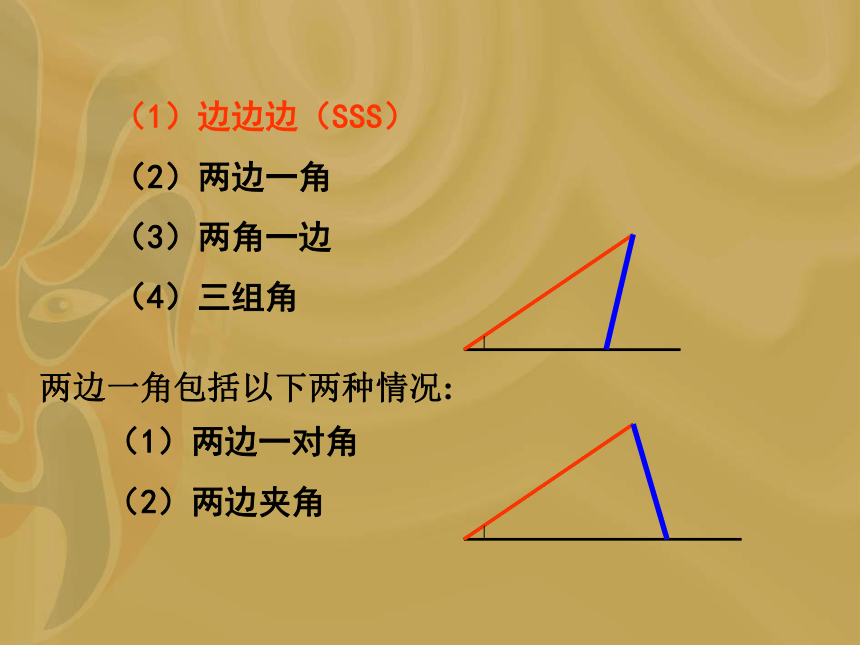
(1)边边边(SSS)
(2)两边一角
(3)两角一边
(4)三组角(1)两边一对角
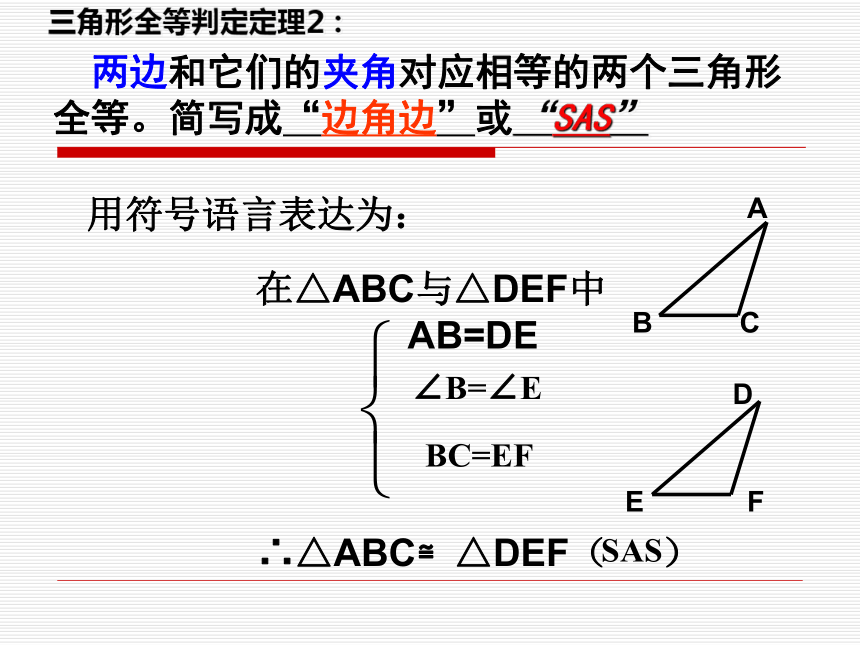
(2)两边夹角两边一角包括以下两种情况:1、画一个三角形,使其两条边长分别为3cm和4cm,并且使它们的夹角为45 °。 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗? 三角形全等判定定理2:用符号语言表达为:在△ABC与△DEF中AB=DE
∴△ABC≌△DEF( ) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
∠B=∠E
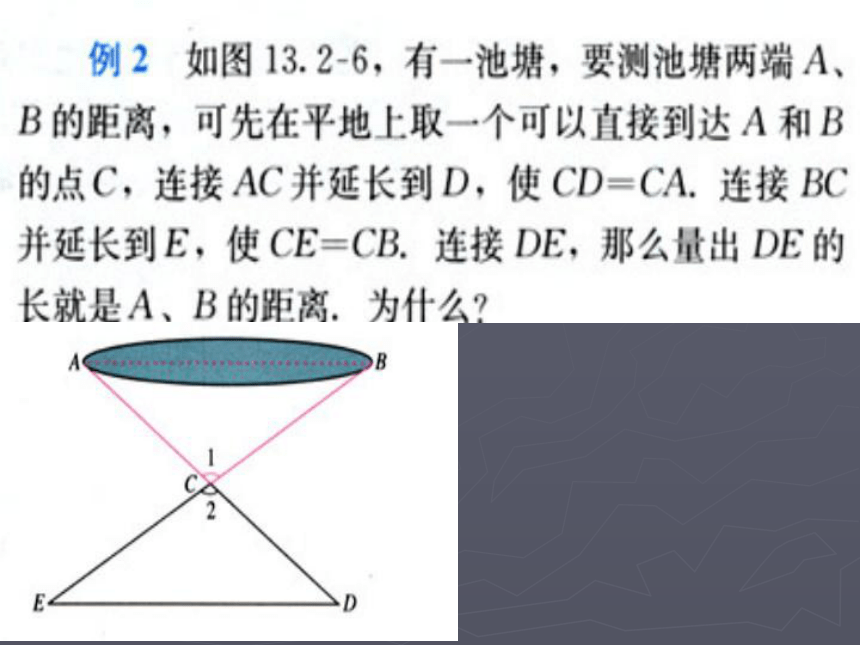
BC=EFSAS探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),你能测出A、B两点的距离吗? AB探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图), AB如果无法直接量出A、B两点的距离,现有一足够长的皮尺。你能设计一种方案,粗略测出
A、B两杆之间的距离吗?。
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用皮尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?( )
∴△ACB≌△DCE( )
∴AB=DE( )在△ACB和△DCE 中∠ACB=∠DCE( )
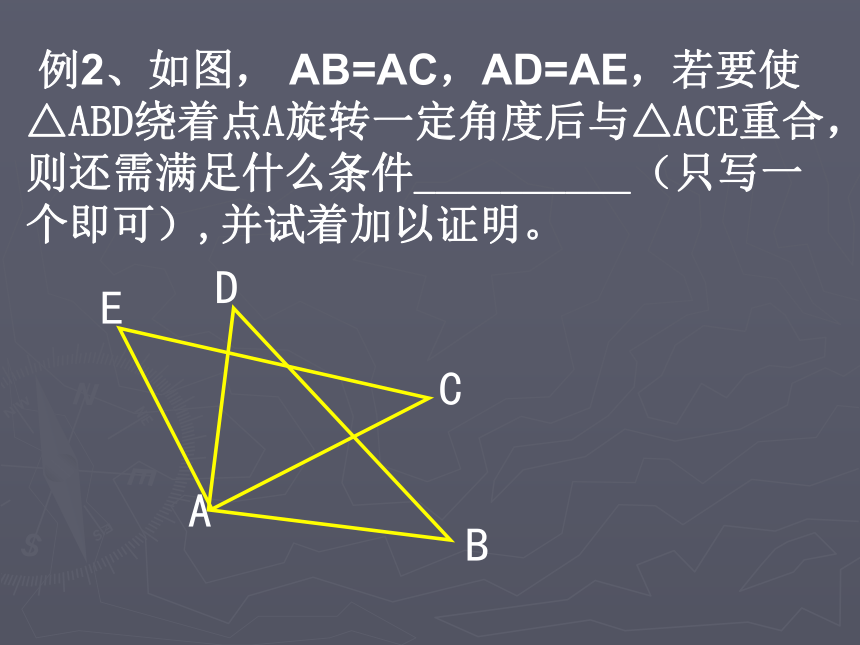
BC=EC( )SAS 例2、如图, AB=AC,AD=AE,若要使△ABD绕着点A旋转一定角度后与△ACE重合,则还需满足什么条件__________(只写一个即可),并试着加以证明。ABCDE课堂小结:2. 用尺规作图:已知两边及其夹角的三角形②两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)1. 三角形全等的条件: ①SSS《数学》( 北师大.七年级 下册 )13.2三角形全等的条件(2)第2课时(1)边边边(SSS)
(2)边角边(SAS)——两边夹角
边边角(SSA)——两边一对角教与学:
1、如图, 在△ABC中,AD┴BC,D为BC的中点,则以下结论不正确的是( )
(A)△ABD≌△ACD
(B)∠B=∠C
(C)AD是∠A的平分线
(D)△ABC是等边三角形ABCD2、如果两个三角形两边对应相等,且其中一边所对的角也相等,那么这两个三角形( )
(A)一定全等
(B)一定不全等
(C)不一定全等
(D)面积相等3、如图, 在△ABC中,AB=AC,BE、CF是中线,则由_______可得△AFC≌△AEBABCEF4、如图, AB=DC,AD=BC,E、F是DB上两点,若∠AFB=1000, ∠DAF=300,则∠CBE=_______ABCDEF4、如图, AB┴AC,AD┴AE,AB=AC,AD=AE,BD交AC、EC于P、F,AD、EC交于点Q,
求证(1) △ABD≌△ACE
(2) BD┴CE ABCDEFPQ精讲精练:
1、如图, 在四边形ABCD中,对角线AC、BD互相平分(即OA=OC,OB=OD),试判断图形中一共有多少对全等三角形。 ABCDO 2、如图, AB=CD,AF=DE,BE=CF,猜测并证明AF与DE的关系?
ABCDEF 3、如图, AB=AC,EB=EC,AE的延长线交BC于D,求证△ABD≌△ACD ABCDE 4、如图, DC=EA,EC=BA,DC┴AC,BA┴AC,垂足分别是C、A,求证BE┴DEABCDE 5、如图, 在AB、AC上各取一点E、D,使AE=AD,连结BD、CE,相交于点O,连结AO,OB=OC,若∠1= ∠2 ,
求证∠B= ∠C。 ABCDE12O 6、如图,已知△ABC中,AD┴BC于D,AD=BD,DE=DC,∠C=500,求∠EBD的度数。ABCDE 练习:
1、如图,已知AE=CF,BE=DF,要证明 △ABE≌△CDF,还需( )ABCDEF2、下列条件,可以确定△ABC和△A′B′C′全等的是( )
(A)BC=BA,B′C′=B′A′,∠B=∠B′
(B) ∠A=∠B′,AC= A′B′ ,AB=B′C′
(C) ∠A=∠A′,AB=B′C′ ,AC=A′C′
(D) BC=B′C′,AC =A′B′,∠B=∠C′3、如图所示,OC 是∠AOB的平分线,请你再添加一个条件,使得AC=BC,并说明你的理由。ABCO4、如图,已知AC=DB,要证明△ABC≌△DCB,只需增加一个条件是___________________ABCDO补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.Let’s go!
(1)边边边(SSS)
(2)两边一角
(3)两角一边
(4)三组角(1)两边一对角
(2)两边夹角两边一角包括以下两种情况:1、画一个三角形,使其两条边长分别为3cm和4cm,并且使它们的夹角为45 °。 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗? 三角形全等判定定理2:用符号语言表达为:在△ABC与△DEF中AB=DE
∴△ABC≌△DEF( ) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
∠B=∠E
BC=EFSAS探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),你能测出A、B两点的距离吗? AB探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图), AB如果无法直接量出A、B两点的距离,现有一足够长的皮尺。你能设计一种方案,粗略测出
A、B两杆之间的距离吗?。
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用皮尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?( )
∴△ACB≌△DCE( )
∴AB=DE( )在△ACB和△DCE 中∠ACB=∠DCE( )
BC=EC( )SAS 例2、如图, AB=AC,AD=AE,若要使△ABD绕着点A旋转一定角度后与△ACE重合,则还需满足什么条件__________(只写一个即可),并试着加以证明。ABCDE课堂小结:2. 用尺规作图:已知两边及其夹角的三角形②两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)1. 三角形全等的条件: ①SSS《数学》( 北师大.七年级 下册 )13.2三角形全等的条件(2)第2课时(1)边边边(SSS)
(2)边角边(SAS)——两边夹角
边边角(SSA)——两边一对角教与学:
1、如图, 在△ABC中,AD┴BC,D为BC的中点,则以下结论不正确的是( )
(A)△ABD≌△ACD
(B)∠B=∠C
(C)AD是∠A的平分线
(D)△ABC是等边三角形ABCD2、如果两个三角形两边对应相等,且其中一边所对的角也相等,那么这两个三角形( )
(A)一定全等
(B)一定不全等
(C)不一定全等
(D)面积相等3、如图, 在△ABC中,AB=AC,BE、CF是中线,则由_______可得△AFC≌△AEBABCEF4、如图, AB=DC,AD=BC,E、F是DB上两点,若∠AFB=1000, ∠DAF=300,则∠CBE=_______ABCDEF4、如图, AB┴AC,AD┴AE,AB=AC,AD=AE,BD交AC、EC于P、F,AD、EC交于点Q,
求证(1) △ABD≌△ACE
(2) BD┴CE ABCDEFPQ精讲精练:
1、如图, 在四边形ABCD中,对角线AC、BD互相平分(即OA=OC,OB=OD),试判断图形中一共有多少对全等三角形。 ABCDO 2、如图, AB=CD,AF=DE,BE=CF,猜测并证明AF与DE的关系?
ABCDEF 3、如图, AB=AC,EB=EC,AE的延长线交BC于D,求证△ABD≌△ACD ABCDE 4、如图, DC=EA,EC=BA,DC┴AC,BA┴AC,垂足分别是C、A,求证BE┴DEABCDE 5、如图, 在AB、AC上各取一点E、D,使AE=AD,连结BD、CE,相交于点O,连结AO,OB=OC,若∠1= ∠2 ,
求证∠B= ∠C。 ABCDE12O 6、如图,已知△ABC中,AD┴BC于D,AD=BD,DE=DC,∠C=500,求∠EBD的度数。ABCDE 练习:
1、如图,已知AE=CF,BE=DF,要证明 △ABE≌△CDF,还需( )ABCDEF2、下列条件,可以确定△ABC和△A′B′C′全等的是( )
(A)BC=BA,B′C′=B′A′,∠B=∠B′
(B) ∠A=∠B′,AC= A′B′ ,AB=B′C′
(C) ∠A=∠A′,AB=B′C′ ,AC=A′C′
(D) BC=B′C′,AC =A′B′,∠B=∠C′3、如图所示,OC 是∠AOB的平分线,请你再添加一个条件,使得AC=BC,并说明你的理由。ABCO4、如图,已知AC=DB,要证明△ABC≌△DCB,只需增加一个条件是___________________ABCDO补充练习:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.Let’s go!
