13.2三角形全等的条件(HL)[上学期]
文档属性
| 名称 | 13.2三角形全等的条件(HL)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-14 13:03:00 | ||
图片预览





文档简介
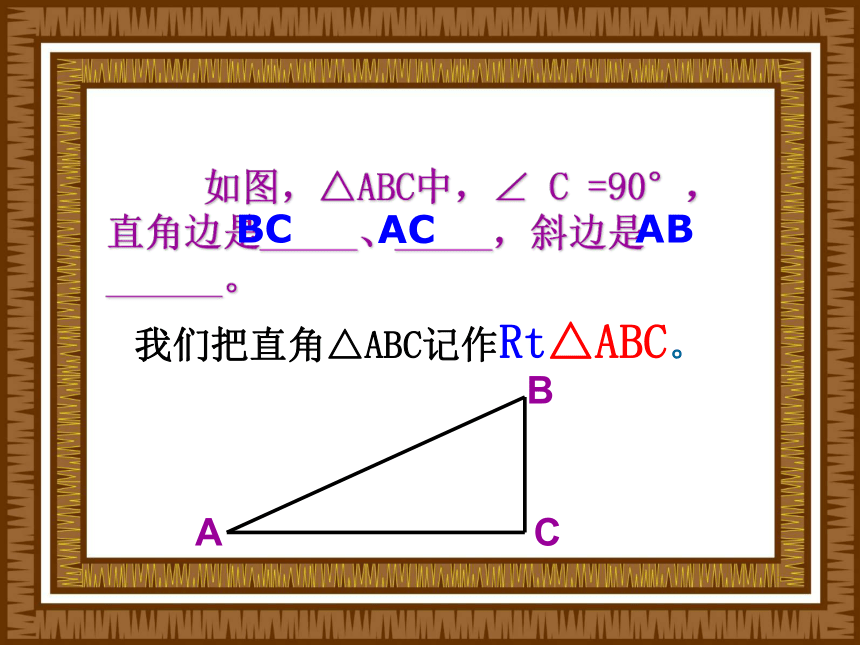
课件33张PPT。授课教师:李晶晶 13.2探索三角形全等的条件 (H L)旧知回顾SSSSASASAAAS 三边对应相等的两个三角形全等。(简写成边 边 边“边边边”或“SSS”)边 角 边“边角边”或“SAS”) 两边和它们夹角对应相等的两个三角形全等。(简写成角 边 角“角边角”或“ASA”) 两角和它们的夹边对应相等的两个三角形全等。(简写成角 角 边 两个角和其中一个角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”) 如图,△ABC中,∠ C =90°,直角边是_____、_____,斜边是______。我们把直角△ABC记作Rt△ABC。ACBCAB1、探索三角形全等的条件之五:
斜边、直角边(HL)。
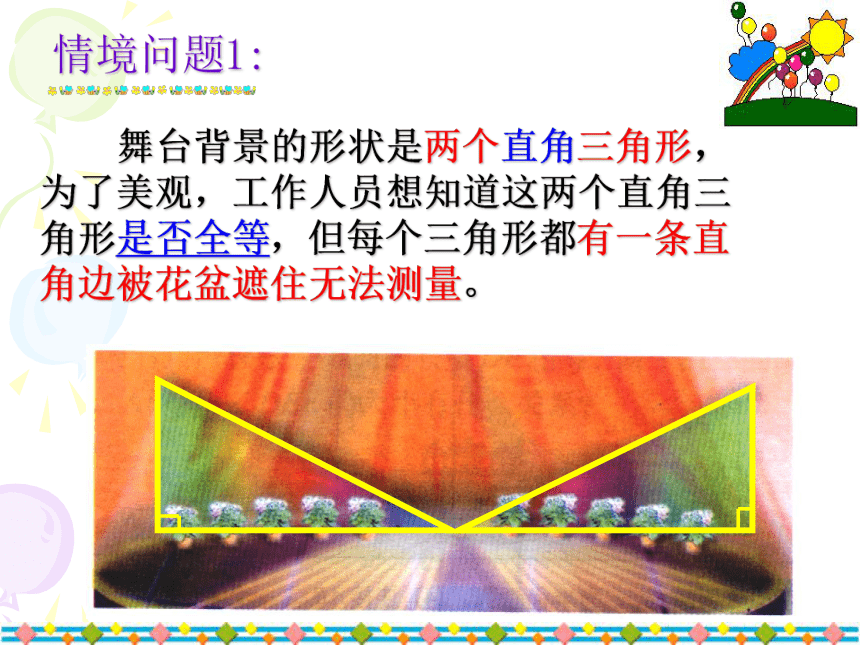
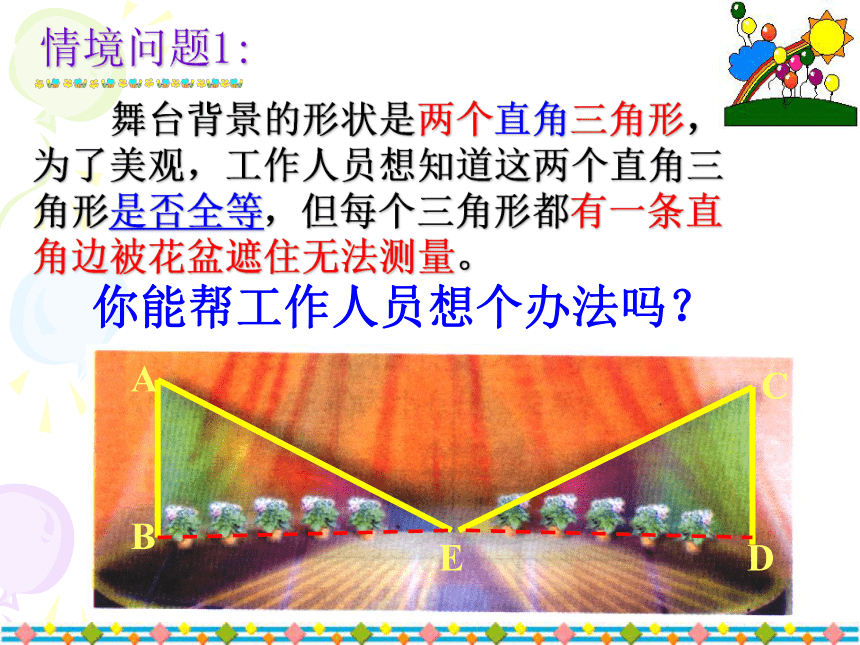
2、学会用HL证明三角形全等。本节课学习目标 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。情境问题1:情境问题1: 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。你能帮工作人员想个办法吗?情境问题1:方法1:测量斜边和一个对应的锐角。(AAS)方法2:测量未被遮住的一条直角边和一个对应的锐角。(ASA)方法3:测量未被遮住的一条直角边和斜边,及其它们的夹角。(SAS)情境问题2: 如果工作人员只带了一个卷尺,能完成这项任务吗? 工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗?情境问题2: 对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗?探 究 活 动
开 始 啦!请你动手画一画尺规作图的方法步骤:1、画∠DC/ E= 90°.2、在射线C/ D上截取C/B/=CB.4、连结B/A/。3、以B/为圆心,以AB为半径画弧,交射线C/ E于点A/.则 △A/ B/ C/ 即是我们要作的三角形。已知Rt△ABC,∠C=90°。
作Rt△A′B′C′ ,使得∠C′= ∠C= 90°,
斜边和任意一条直角边对应相等。探 究 8 用剪刀把你所画的三角形剪下来,与原三角形进行比较,看是否能重合?亲 自 实 践探索发现的规律是: 斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt △DEF中 通过刚才的探索,发现工作人员的做法是完全正确的。如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD(HL)∴BC=AD(全等三角形对应边相等)新知应用:(1)如图,AB⊥BC,AD⊥DC,
AB=AD。 求证:∠1=∠2 。证明: ∵AB⊥BC,AD⊥DC,
∴∠B和∠D都是直角。∴Rt△ABC≌ Rt △ADC(HL)∴ ∠1=∠2 (全等三角形对应角相等)在Rt△ABC和Rt△ADC中,演练空间!(2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?课本103页练习CD 与CE 相等吗?证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB (全等三角形对应边相等)在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(3)如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF
斜边和一条直角边对应相等的两个直角三角形全等(HL).畅所欲言! (1)如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。拓展探究1 (2)如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?拓展探究2解:在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°. 如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.求证:MB=MD,
ME=MF。ABCDEFM拓 展 探 究 3如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于点G,DE⊥AG于E,且DE=AB,∠1=∠2.根据上述条件,请在图中找出一对全等三角形,并证明你的结论. 课后思考题课 后 作 业(1)课本104页
练习题7、8。(2)填好课堂评价表。谢谢指导!再 见
斜边、直角边(HL)。
2、学会用HL证明三角形全等。本节课学习目标 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。情境问题1:情境问题1: 舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量。你能帮工作人员想个办法吗?情境问题1:方法1:测量斜边和一个对应的锐角。(AAS)方法2:测量未被遮住的一条直角边和一个对应的锐角。(ASA)方法3:测量未被遮住的一条直角边和斜边,及其它们的夹角。(SAS)情境问题2: 如果工作人员只带了一个卷尺,能完成这项任务吗? 工作人员是这样做的,他测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”。你相信他的结论吗?情境问题2: 对于两个直角三角形,若满足一条直角边和一条斜边对应相等时,这两个直角三角形全等吗?探 究 活 动
开 始 啦!请你动手画一画尺规作图的方法步骤:1、画∠DC/ E= 90°.2、在射线C/ D上截取C/B/=CB.4、连结B/A/。3、以B/为圆心,以AB为半径画弧,交射线C/ E于点A/.则 △A/ B/ C/ 即是我们要作的三角形。已知Rt△ABC,∠C=90°。
作Rt△A′B′C′ ,使得∠C′= ∠C= 90°,
斜边和任意一条直角边对应相等。探 究 8 用剪刀把你所画的三角形剪下来,与原三角形进行比较,看是否能重合?亲 自 实 践探索发现的规律是: 斜边和一条直角边对应相等的两个三角形全等,简写为“斜边、直角边”或“HL”。数学语言:∵在Rt△ABC和Rt △DEF中 通过刚才的探索,发现工作人员的做法是完全正确的。如图:AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.证明: ∵AC⊥BC,BD⊥AD,
∴∠C和∠D都是直角。在Rt△ABC和Rt△BAD中,∴Rt△ABC≌ Rt △BAD(HL)∴BC=AD(全等三角形对应边相等)新知应用:(1)如图,AB⊥BC,AD⊥DC,
AB=AD。 求证:∠1=∠2 。证明: ∵AB⊥BC,AD⊥DC,
∴∠B和∠D都是直角。∴Rt△ABC≌ Rt △ADC(HL)∴ ∠1=∠2 (全等三角形对应角相等)在Rt△ABC和Rt△ADC中,演练空间!(2)如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?课本103页练习CD 与CE 相等吗?证明: ∵DA⊥AB,EB⊥AB,
∴∠A和∠B都是直角。∴Rt△ACD≌ Rt △BCE(HL)∴ DA=EB (全等三角形对应边相等)在Rt△ACD和Rt△BCE中,又∵C是AB的中点,
∴AC=BC ∵C到D、E的速度、时间相同,
∴DC=EC(3)如图,AB=CD,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.课本103页练习∵CE=BF
∴CE-EF=BF-EF
即CF=BE。
证明:∵ AE⊥BC,DF⊥BC
∴△ABE和△DCF都是直角三角形。又∵CE=BF ∴CE-EF=BF-EF
即CF=BE。 在Rt△ABE和Rt△DCF中∴Rt△ABE≌Rt△DCF(HL) ∴AE=DF
斜边和一条直角边对应相等的两个直角三角形全等(HL).畅所欲言! (1)如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。拓展探究1 (2)如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系?拓展探究2解:在Rt△ABC和Rt△DEF中,∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°. 如图,E,F分别为线段AC上的两个点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.求证:MB=MD,
ME=MF。ABCDEFM拓 展 探 究 3如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于点G,DE⊥AG于E,且DE=AB,∠1=∠2.根据上述条件,请在图中找出一对全等三角形,并证明你的结论. 课后思考题课 后 作 业(1)课本104页
练习题7、8。(2)填好课堂评价表。谢谢指导!再 见
