13.2三角形全等的条件(2)[上学期]
文档属性
| 名称 | 13.2三角形全等的条件(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 942.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-24 00:00:00 | ||
图片预览

文档简介
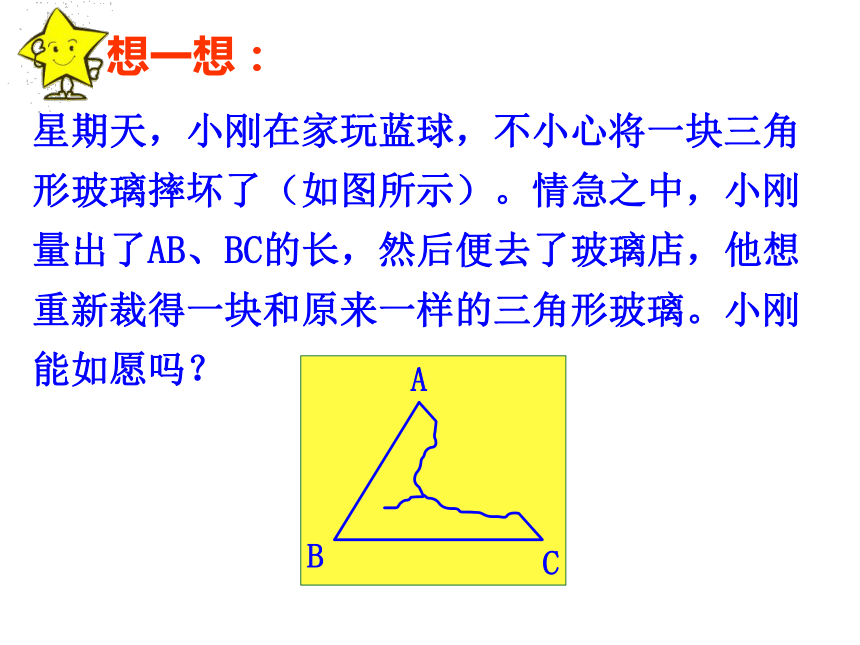
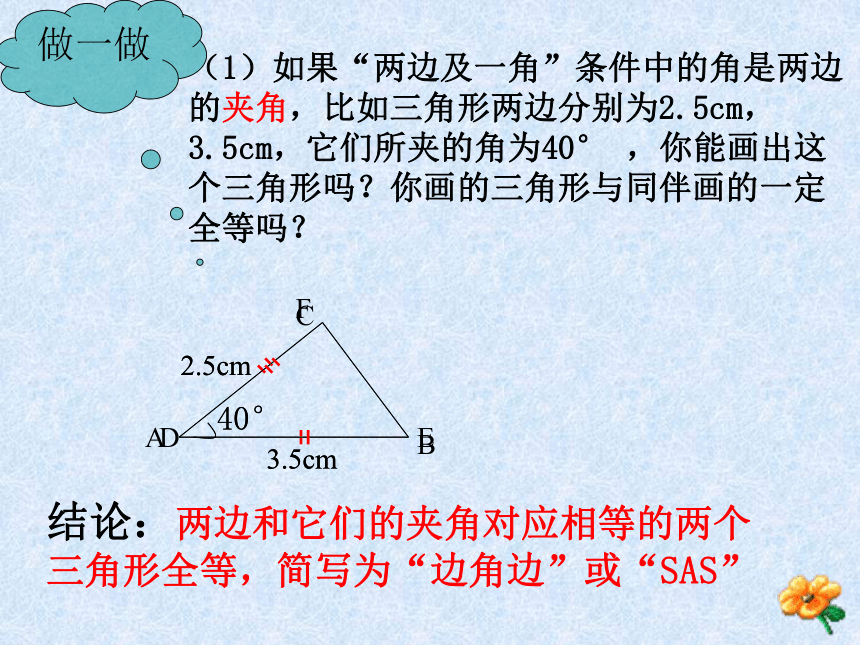
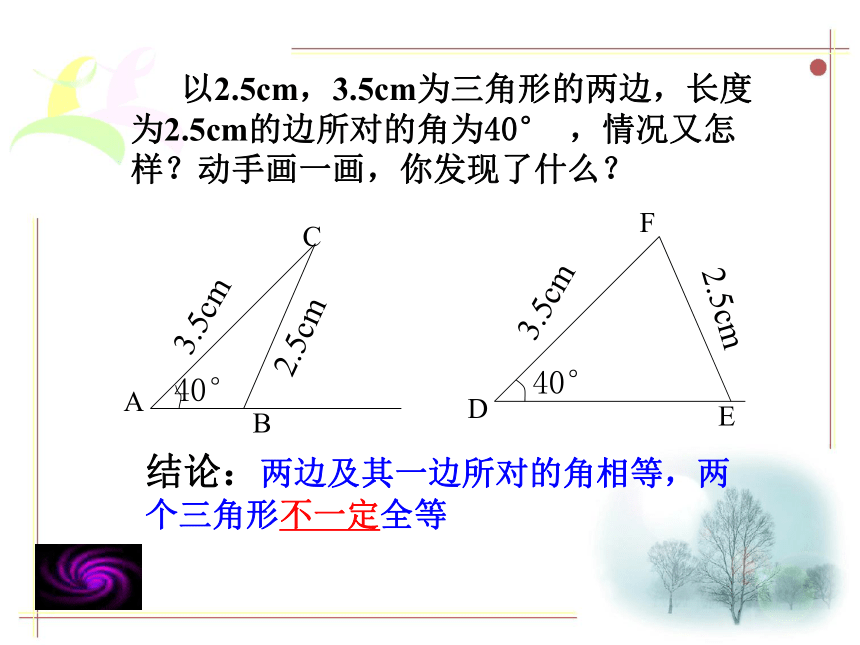
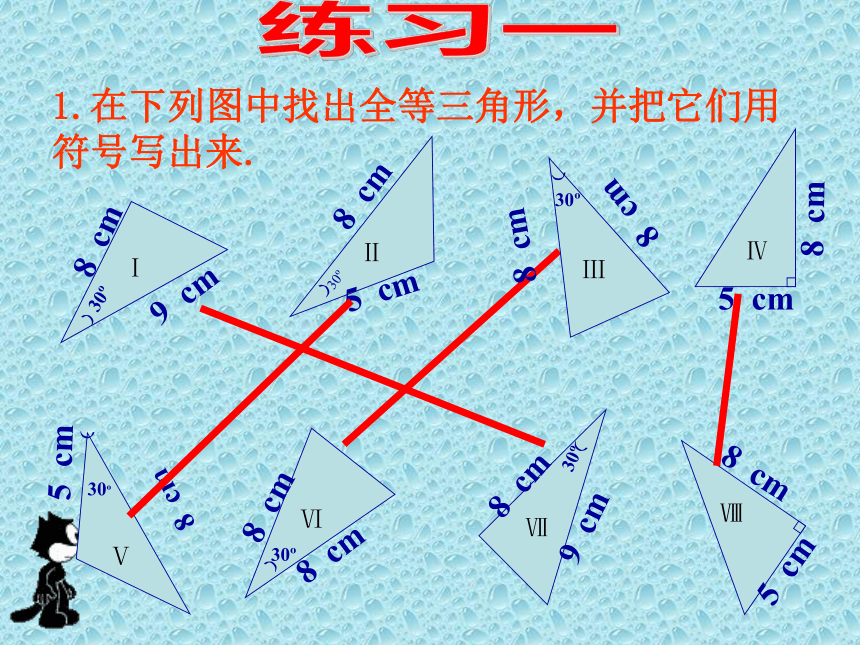
课件22张PPT。1.5 三角形全等的条件(2)星期天,小刚在家玩蓝球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?做一做(1)如果“两边及一角”条件中的角是两边的夹角,比如三角形两边分别为2.5cm,3.5cm,它们所夹的角为40° ,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS” 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等1.在下列图中找出全等三角形,并把它们用
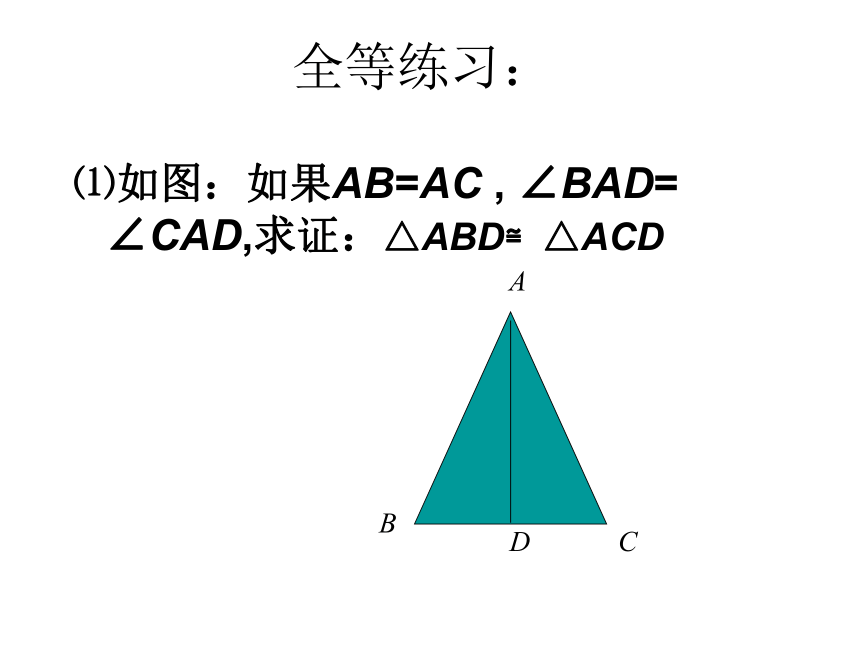
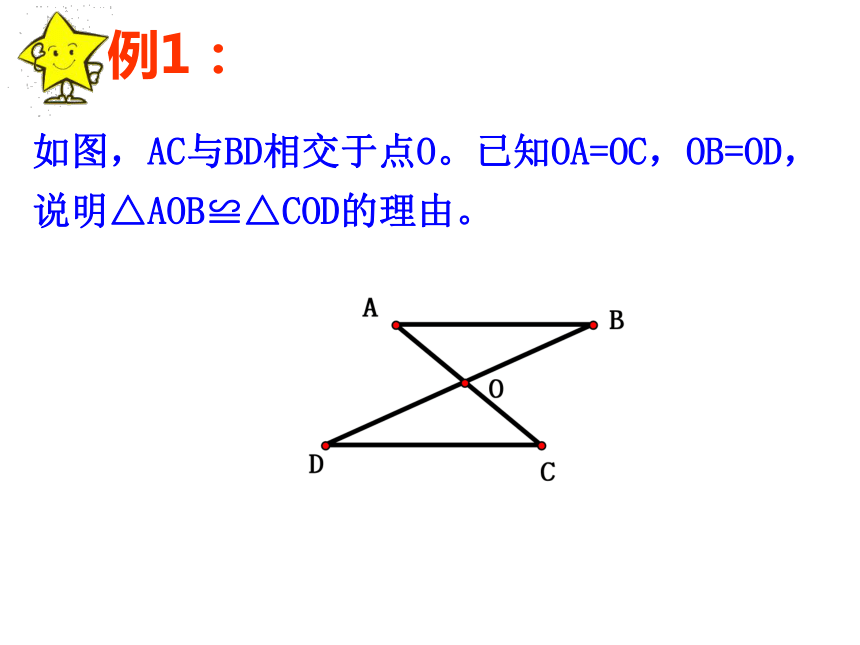
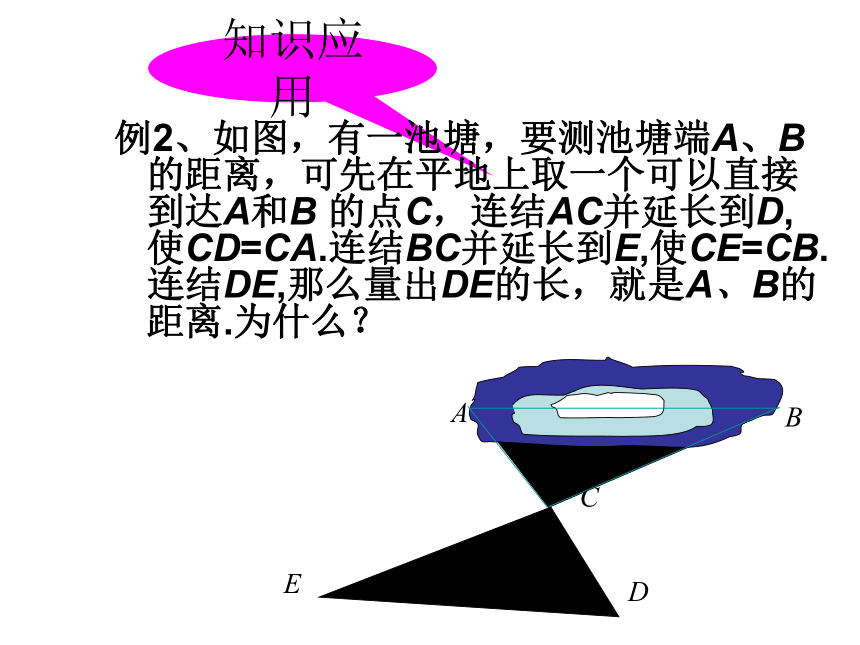
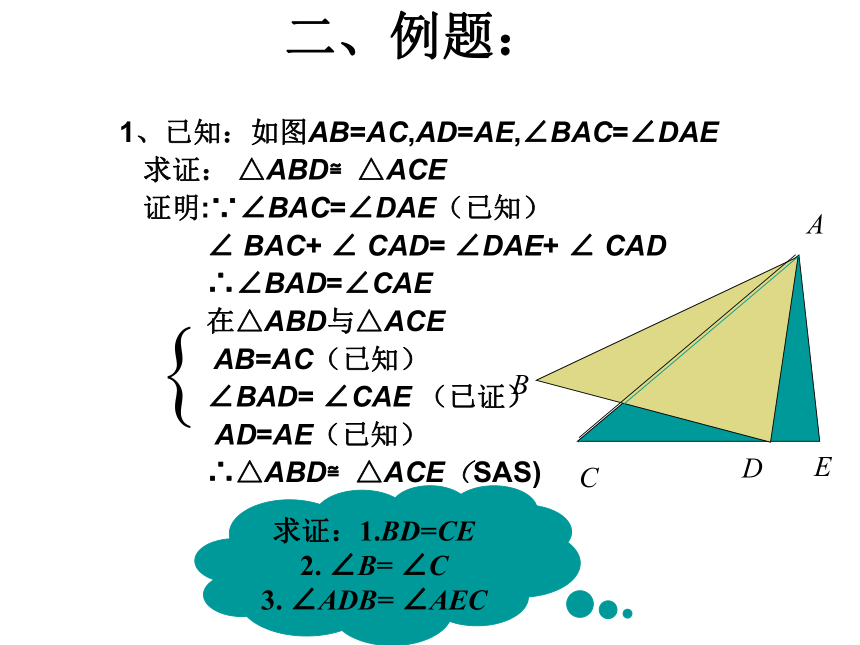
符号写出来.练习一全等练习:⑴如图:如果AB=AC , ∠BAD= ∠CAD,求证:△ABD≌△ACDABCD如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?二、例题:1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
∴△ABD≌△ACE(SAS)ABD CE求证:1.BD=CE
2. ∠B= ∠C
3. ∠ADB= ∠AEC
∟ ADBCE变式1:已知:如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE. 求证: ⑴ △DAC≌△EABBE=DC
∠B= ∠ C
∠ D= ∠ E
BE⊥CD FMABCED变式2:已知,如图等边△AEB与等 边△BCD在线段AC的同侧 求证: △ABD≌△EBC变式3:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
线段垂直平分线上的点和这条线段两个端点的距离相等。小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、注意哦!“边边角”不能判定两个三角形全等与你同桌交流一下,然后请说一说,你本节课学习了些什么?作业布置1、课本第25页
2、作业本(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSAS练习二AD=AD2.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=AD
符号写出来.练习一全等练习:⑴如图:如果AB=AC , ∠BAD= ∠CAD,求证:△ABD≌△ACDABCD如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。知识应用例2、如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连结AC并延长到D, 使CD=CA.连结BC并延长到E,使CE=CB. 连结DE,那么量出DE的长,就是A、B的距离.为什么?二、例题:1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE
求证: △ABD≌△ACE
证明:∵∠BAC=∠DAE(已知)
∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD
∴∠BAD=∠CAE
在△ABD与△ACE
AB=AC(已知)
∠BAD= ∠CAE (已证)
AD=AE(已知)
∴△ABD≌△ACE(SAS)ABD CE求证:1.BD=CE
2. ∠B= ∠C
3. ∠ADB= ∠AEC
∟ ADBCE变式1:已知:如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE. 求证: ⑴ △DAC≌△EABBE=DC
∠B= ∠ C
∠ D= ∠ E
BE⊥CD FMABCED变式2:已知,如图等边△AEB与等 边△BCD在线段AC的同侧 求证: △ABD≌△EBC变式3:已知如图△ABD与△ACE均为等边三角形,求证:DC=BE想一想:
你还能写出哪些结论
线段垂直平分线上的点和这条线段两个端点的距离相等。小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH说一说1、今天我们学习哪种方法判定两三角形全等?答:边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?答:SSS、SAS、注意哦!“边边角”不能判定两个三角形全等与你同桌交流一下,然后请说一说,你本节课学习了些什么?作业布置1、课本第25页
2、作业本(2).如图,在△AEC和△ADB中,已知AE=AD,AC=AB请说明△AEC ≌ △ADB的理由。____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )AEADACABSAS解:在△AEC和△ADB中如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件?1.若AB=AC,则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAB=AC∠BAD= ∠CADSAS练习二AD=AD2.如图,要证△ACB≌ △ADB ,至少选用哪些条件可ABCD△ACB≌ △ADBSAS证得△ACB≌ △ADBAB=AB∠CAB= ∠ DABAC=AD
