13.3角的平分线的性质[上学期]
文档属性
| 名称 | 13.3角的平分线的性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 702.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-19 20:45:00 | ||
图片预览



文档简介
课件16张PPT。HUANYINGGUANGLIN13.3三角形角平分线的性质学习目标
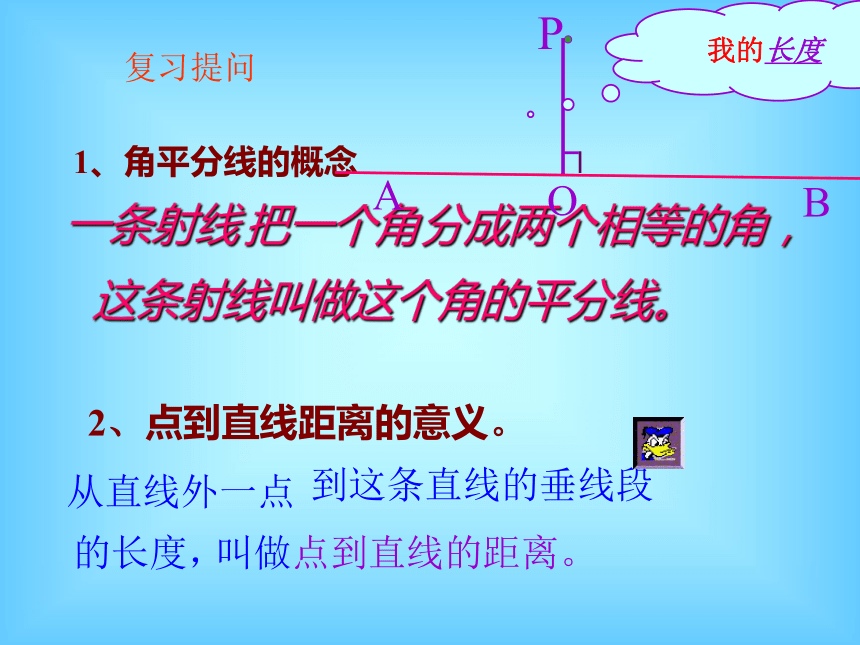
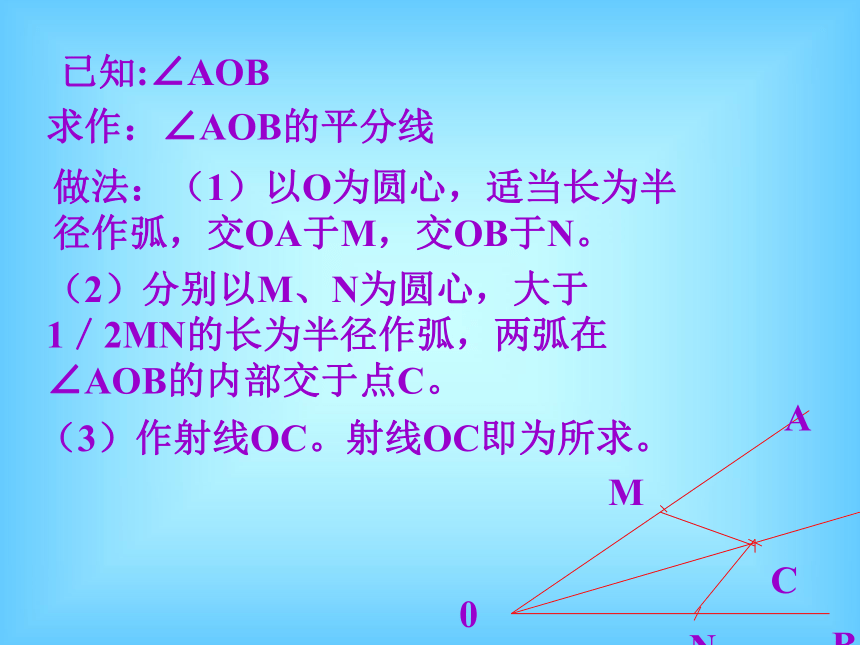
掌握角的平分线性质和判定,并能应用它解决问题。 角的平分线除了平分角的性质,还有其他的性质吗?想一想复习提问1、角平分线的概念 2、点到直线距离的意义。一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。已知:∠AOB求作:∠AOB的平分线做法:(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。(2)分别以M、N为圆心,大于 1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。(3)作射线OC。射线OC即为所求。
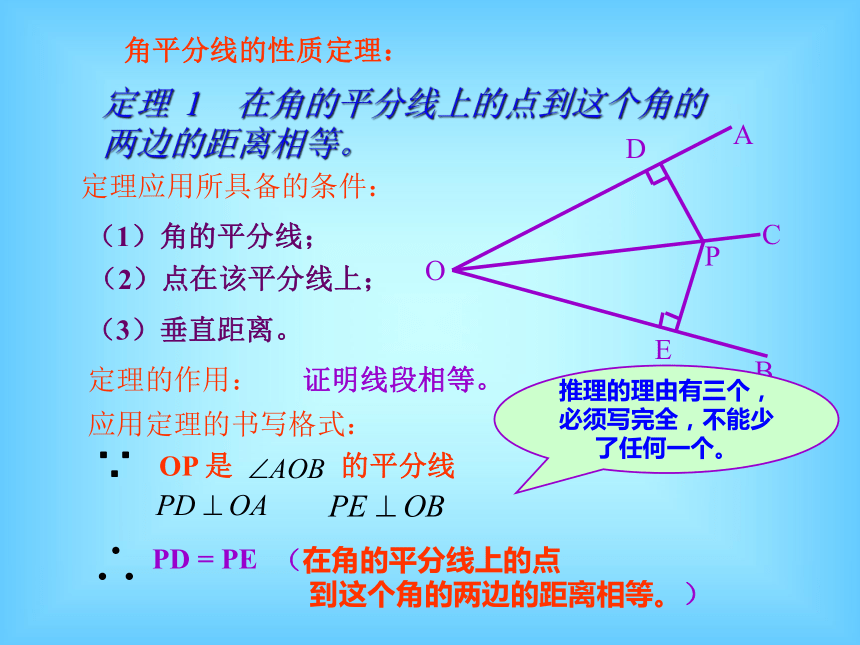
A0BMNC角平分线的性质定理:定理 1 在角的平分线上的点到这个角的两边的距离相等。定理应用所具备的条件:定理的作用: 证明线段相等。应用定理的书写格式:PD = PE(在角的平分线上的点
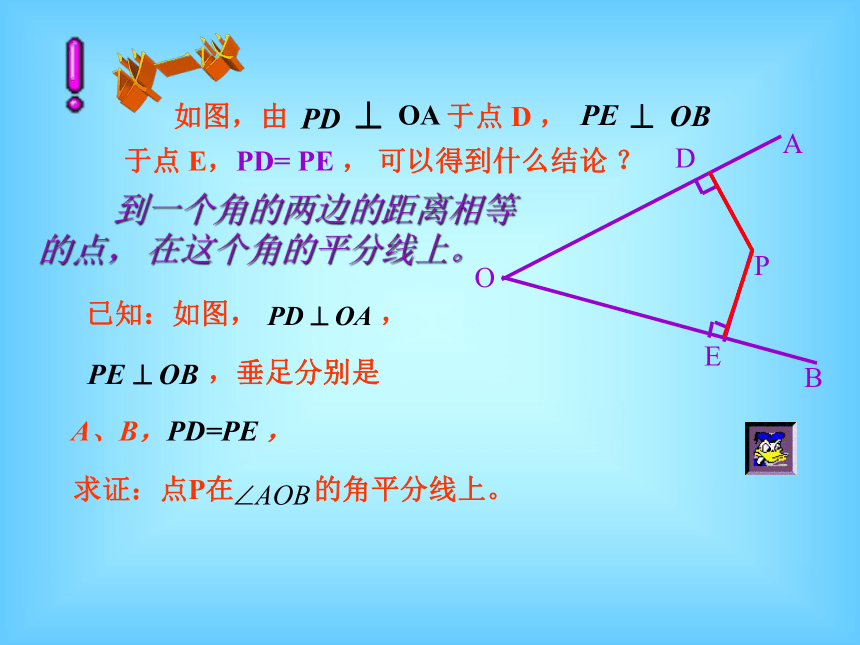
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。 如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ? 议一议 到一个角的两边的距离相等的点, 在这个角的平分线上。 到一个角的两边的距离相等的点, 在这个角的平分线上。证明:作射线OP 在 Rt△PDO 和Rt△PEO 中,( HL)(全等三角形的对应角相等) OP = OP (公共边)PD = PE ( 已 知 )定理 2定理 2的应用书写格式:PD= PE (到一个角的
两边的距离相等的点, 在这个角的平分线上)
∵定理 1 在角的平分线上的点到这个角的两边的距离相等。定理 2 到一个角的两边的距离相等的点, 在这个角的平分线上。PD = PE用途:证线段相等用途:判定一条射线是角平分线我们利用折纸和尺规作图的方法都发现三角形的三条角平分线相交于一点,你能证明这个结论吗?如图,设△ABC的角平分线BM,CN相交于点P,你能证明点P在∠BAC的平分线上吗?过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D,
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE(角平分线上的点到这个角的两边的距离相等)
同理,PE=PF,
∴PD=PF
∴点P在△BAC的平分线上(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上)。∴△ABC三条角平分线相交于点P。(1)角平分线的性质定理及其逆定理及作用;(2)用这两个定理,一定要具备两个垂直距离(即点到直线的距离),证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样做实际是重新证了一次定理)。小结:(3)怎样找三角形内到三角形三边距离相等的点。随堂练习3 已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F。
求证:点F在∠DAE的平分线上。(六)作业:
作业本(110页2、3)
掌握角的平分线性质和判定,并能应用它解决问题。 角的平分线除了平分角的性质,还有其他的性质吗?想一想复习提问1、角平分线的概念 2、点到直线距离的意义。一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。已知:∠AOB求作:∠AOB的平分线做法:(1)以O为圆心,适当长为半径作弧,交OA于M,交OB于N。(2)分别以M、N为圆心,大于 1/2MN的长为半径作弧,两弧在∠AOB的内部交于点C。(3)作射线OC。射线OC即为所求。
A0BMNC角平分线的性质定理:定理 1 在角的平分线上的点到这个角的两边的距离相等。定理应用所具备的条件:定理的作用: 证明线段相等。应用定理的书写格式:PD = PE(在角的平分线上的点
到这个角的两边的距离相等。)∵推理的理由有三个,必须写完全,不能少了任何一个。 如图,由 于点 D , 于点 E,PD= PE , 可以得到什么结论 ? 议一议 到一个角的两边的距离相等的点, 在这个角的平分线上。 到一个角的两边的距离相等的点, 在这个角的平分线上。证明:作射线OP 在 Rt△PDO 和Rt△PEO 中,( HL)(全等三角形的对应角相等) OP = OP (公共边)PD = PE ( 已 知 )定理 2定理 2的应用书写格式:PD= PE (到一个角的
两边的距离相等的点, 在这个角的平分线上)
∵定理 1 在角的平分线上的点到这个角的两边的距离相等。定理 2 到一个角的两边的距离相等的点, 在这个角的平分线上。PD = PE用途:证线段相等用途:判定一条射线是角平分线我们利用折纸和尺规作图的方法都发现三角形的三条角平分线相交于一点,你能证明这个结论吗?如图,设△ABC的角平分线BM,CN相交于点P,你能证明点P在∠BAC的平分线上吗?过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D,
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE(角平分线上的点到这个角的两边的距离相等)
同理,PE=PF,
∴PD=PF
∴点P在△BAC的平分线上(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上)。∴△ABC三条角平分线相交于点P。(1)角平分线的性质定理及其逆定理及作用;(2)用这两个定理,一定要具备两个垂直距离(即点到直线的距离),证明过程中要直接应用这两个定理,而不要去寻找全等三角形(这样做实际是重新证了一次定理)。小结:(3)怎样找三角形内到三角形三边距离相等的点。随堂练习3 已知:如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F。
求证:点F在∠DAE的平分线上。(六)作业:
作业本(110页2、3)
