轴对称(2)[上学期]
图片预览







文档简介
课件24张PPT。美妙的轴对称椒江二中 林英对称的起源 对称的概念源于数学。对于“对称”在生物现象中的研究,始于1884年的pasteur的工作。“对称”在天文学上的研究,则开始于二千年前的古希腊人。20世纪的物理学家们研究中发现:对称的重要性在与日俱增。
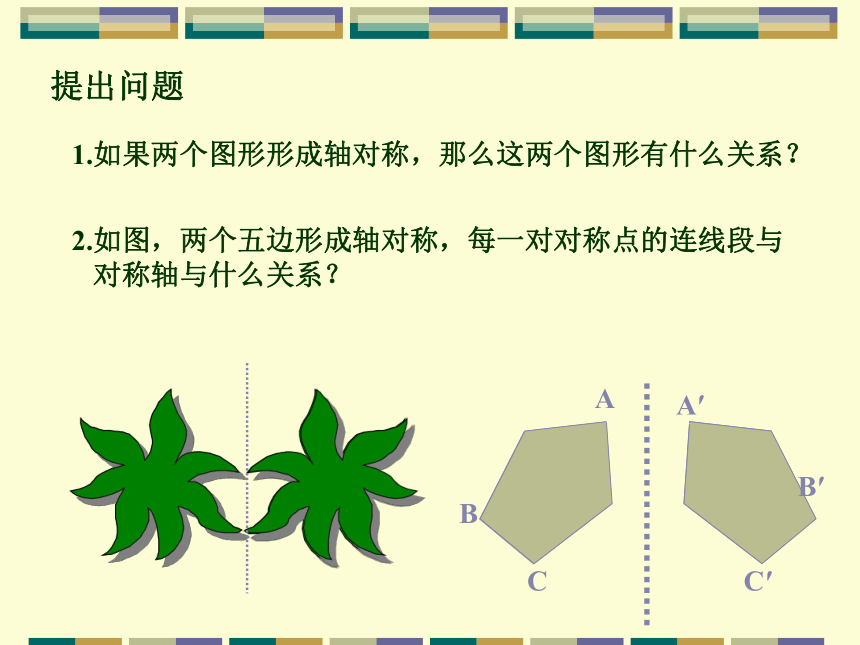
美国数学家赫尔曼 韦尔指出:“对称,尽管你可以规定其含义或宽或窄,而从古到今都是人们用来理解和创造秩序、美妙以及尽善尽美的一种思想。”对称原理乃是数学中“最有力量和最优雅”的解题方法之一。美妙的对称A′ABCB′C′ 提出问题1.如果两个图形形成轴对称,那么这两个图形有什么关系? 2.如图,两个五边形成轴对称,每一对对称点的连线段与
对称轴与什么关系?实验探究3.想一想:
上述性质是对两个成轴对称的图形来说的,如果
是一个轴对称图形,那么它的对应点的连线与对
称轴之间是否也有同样的关系呢?
1..折一折:
(1)从最简单的两点开始2.说一说:
观察图形,线段AB
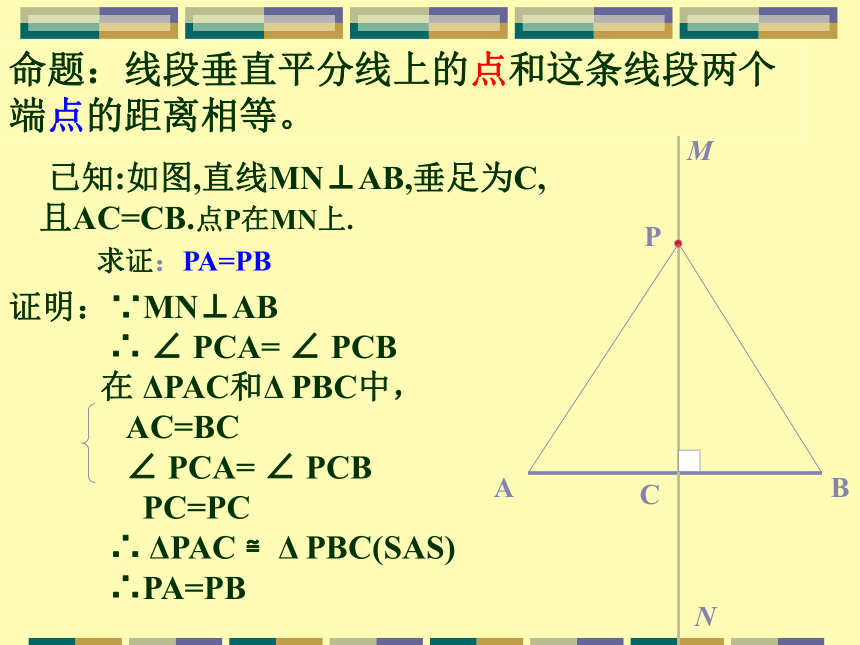
与m的位置关系?1.线段的垂直平分线的定义经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线2.图形轴对称的性质如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.归纳新概念学习新性质合作探究探究1:连接木条L与AB钉在一起,L垂直平分AB, 是L上的点,分别量一量点 到A与B的距离,你有什么发现? 命题:线段垂直平分线上的点和这条线段两个端点的距离相等。CCPA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点和这条线段两个端点的距离相等C性质定理:线段垂直平分线上的点和这条线段两个端 点的距离相等。PA=PB点P在线段AB的垂直平分线上?逆命题:和一条线段两个端点距离相等的点,在这条线 段的垂直平分线上。探究 2:二、逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。一、性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;应用新知:结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(性质定理).
同理 PB=PC.
∴PA=PB=PC. 椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题11、求作一点P,使它和已知△ABC的三个顶点距离相等.实际问题1京 石 高 速 公 路ABL实际问题2 在某高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?运用新知:2、如图,在直线L上求作一点P,使PA=PB.实际问题2数学问题源于生活实践,反过来数学又为生活实践服务京 石 高 速 公 路AL实际问题2的变形 运用新知:在某高速公路L的同侧,有两个化工厂A、B,市政府计划在公路边上修建一所医院,问医院的院址应选在何处使总路程最短?BA’C3.如图,在L上找一点,使AC+CB
是最小值。数学问题源于生活实践,反过来数学又为生活实践服务小结:一、性质定理:线段垂直平分线上的点
和这条线段两个端点的距离相等。二、逆定理:和一条线段两个端点距离
相等的点,在这条线段的垂直平分线上。三、线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两上端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线这节课你学会了什么?你有什么新的收获?作业布置:必做题:1.作业本
2.教科书第125页第3题,第126页第5,9题。
选做题:1.教科书第126页第11题,第127页第12题。再 见2005年11月18日
美国数学家赫尔曼 韦尔指出:“对称,尽管你可以规定其含义或宽或窄,而从古到今都是人们用来理解和创造秩序、美妙以及尽善尽美的一种思想。”对称原理乃是数学中“最有力量和最优雅”的解题方法之一。美妙的对称A′ABCB′C′ 提出问题1.如果两个图形形成轴对称,那么这两个图形有什么关系? 2.如图,两个五边形成轴对称,每一对对称点的连线段与
对称轴与什么关系?实验探究3.想一想:
上述性质是对两个成轴对称的图形来说的,如果
是一个轴对称图形,那么它的对应点的连线与对
称轴之间是否也有同样的关系呢?
1..折一折:
(1)从最简单的两点开始2.说一说:
观察图形,线段AB
与m的位置关系?1.线段的垂直平分线的定义经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线2.图形轴对称的性质如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.归纳新概念学习新性质合作探究探究1:连接木条L与AB钉在一起,L垂直平分AB, 是L上的点,分别量一量点 到A与B的距离,你有什么发现? 命题:线段垂直平分线上的点和这条线段两个端点的距离相等。CCPA=PB点P在线段AB的垂直平分线上线段垂直平分线上的点和这条线段两个端点的距离相等C性质定理:线段垂直平分线上的点和这条线段两个端 点的距离相等。PA=PB点P在线段AB的垂直平分线上?逆命题:和一条线段两个端点距离相等的点,在这条线 段的垂直平分线上。探究 2:二、逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。一、性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等。三、 线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;应用新知:结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(性质定理).
同理 PB=PC.
∴PA=PB=PC. 椒江区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。ABC实际问题11、求作一点P,使它和已知△ABC的三个顶点距离相等.实际问题1京 石 高 速 公 路ABL实际问题2 在某高速公路L的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?运用新知:2、如图,在直线L上求作一点P,使PA=PB.实际问题2数学问题源于生活实践,反过来数学又为生活实践服务京 石 高 速 公 路AL实际问题2的变形 运用新知:在某高速公路L的同侧,有两个化工厂A、B,市政府计划在公路边上修建一所医院,问医院的院址应选在何处使总路程最短?BA’C3.如图,在L上找一点,使AC+CB
是最小值。数学问题源于生活实践,反过来数学又为生活实践服务小结:一、性质定理:线段垂直平分线上的点
和这条线段两个端点的距离相等。二、逆定理:和一条线段两个端点距离
相等的点,在这条线段的垂直平分线上。三、线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两上端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线这节课你学会了什么?你有什么新的收获?作业布置:必做题:1.作业本
2.教科书第125页第3题,第126页第5,9题。
选做题:1.教科书第126页第11题,第127页第12题。再 见2005年11月18日
