人教版数学四年级上空间与图形复习 课件(42张PPT)
文档属性
| 名称 | 人教版数学四年级上空间与图形复习 课件(42张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-13 09:02:44 | ||
图片预览







文档简介
(共42张PPT)
空间与图形
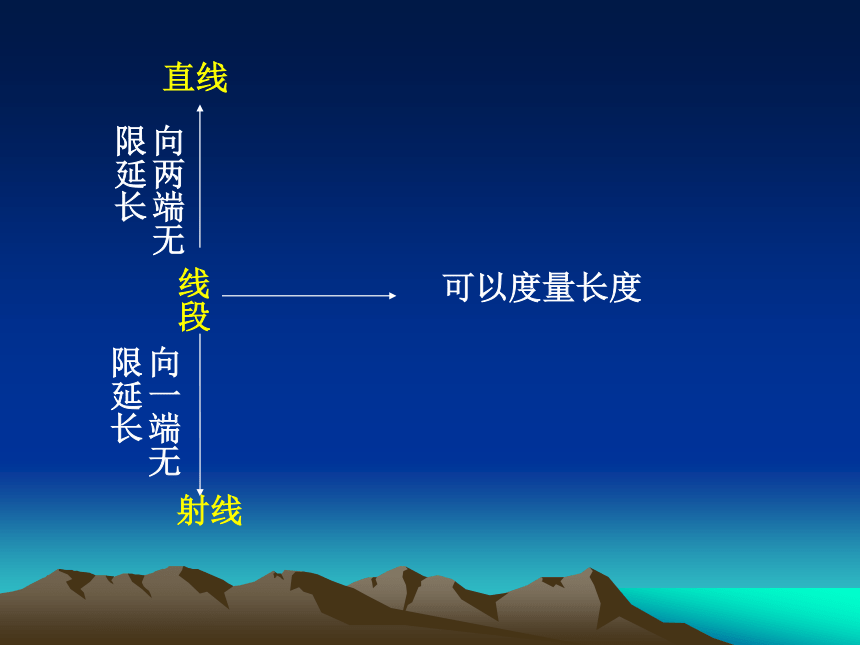
“五线”——直线、射线、线段、垂线、平行线;
“五角”——锐角、直角、钝角、平角、周角。
直线
线段
射线
可以度量长度
向两端无限延长
向一端无限延长
2.任意画出两条直线
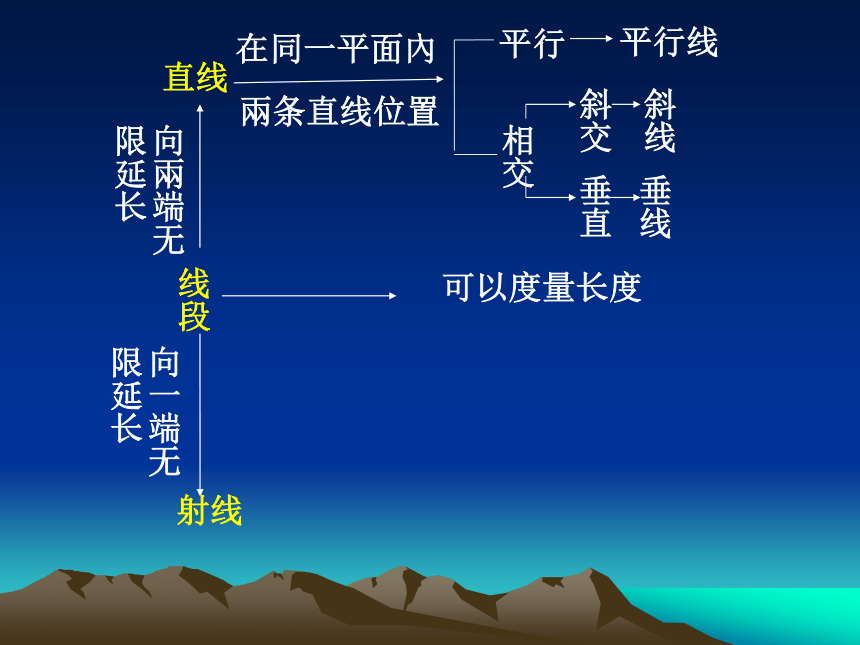
直线
线段
射线
平行
相交
可以度量长度
平行线
斜交
垂直
斜线
垂线
向兩端无限延长
向一端无限延长
在同一平面內
兩条直线位置
3.用两条射线画角
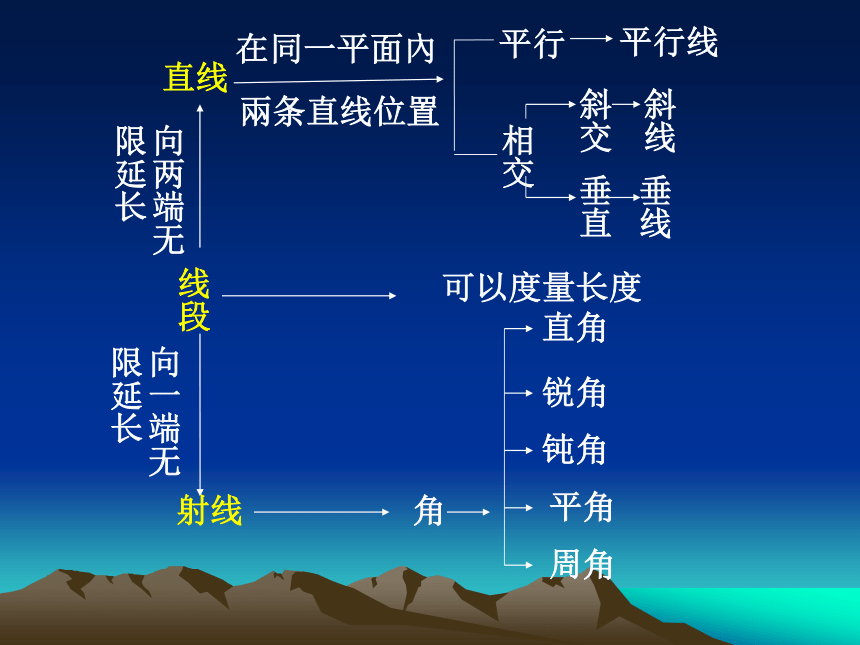
直线
线段
射线
平行
相交
可以度量长度
角
直角
锐角
钝角
平角
周角
平行线
斜交
垂直
斜线
垂线
向两端无限延长
向一端无限延长
在同一平面內
兩条直线位置
1.火眼金睛辨对错。
(1)一条射线长10厘米。 ( )
(2)过两点只能画出一条直线。 ( )
(3)互相垂直的两条直线相交成4个角,4个角都是直角。 ( )
(4)不相交的两条直线叫平行线。 ( )
(5)大于90。的角是钝角。 ( )
(6)平角就是一条直线。 ( )
(7)用一个10倍的放大镜看一个10度的角就是100度。
( )
(8)小明画了一条10厘米长的直线。 ( )
(9)过直线外一点只能画一条直线与这条直线平行。
( )
2.巧画图形我能行。
(1) 清你用量角器画一个135度的角。你还能用其他方法画135度的角吗 请你把方法写出来。
2.巧画图形我能行。
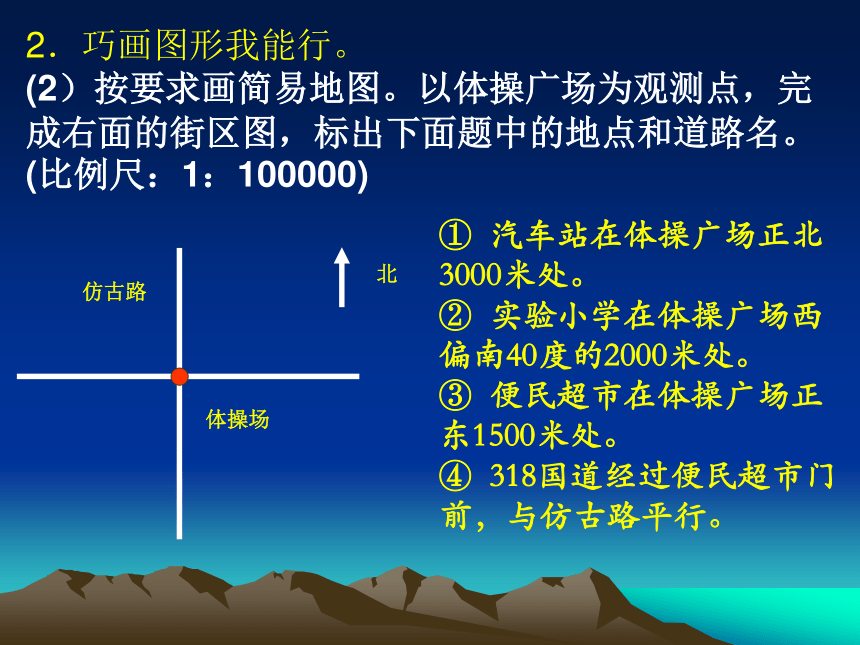
(2)按要求画简易地图。以体操广场为观测点,完成右面的街区图,标出下面题中的地点和道路名。(比例尺:1:100000)
北
仿古路
体操场
① 汽车站在体操广场正北3000米处。
② 实验小学在体操广场西偏南40度的2000米处。
③ 便民超市在体操广场正东1500米处。
④ 318国道经过便民超市门前,与仿古路平行。
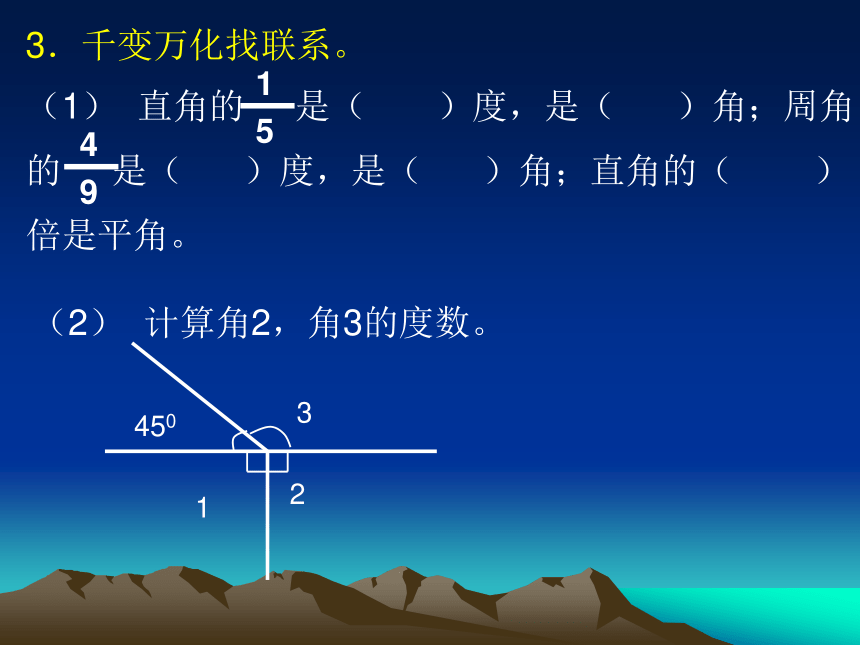
3.千变万化找联系。
(1) 直角的 是( )度,是( )角;周角
的 是( )度,是( )角;直角的( )
倍是平角。
1
5
4
9
(2) 计算角2,角3的度数。
1
2
3
450
在这一部分中,主要复习“七形”——长方形、正方形、平行四边形、三角形、梯形、圆、扇形(选学内容) 。
平面图形
三角形
四边形
平行四边形
长方形
正方形
梯形
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
正三角形
任意梯形
直角梯形
等腰梯形
圆
扇形
两组对边分别平行
只有一组对边平行
四个直角
四边相等
按角分
按边分
已学平面图形
不封闭的平面图形(“五线” 和“五角” )
封闭的平面图形(“七形”)
复习题
1.辨一辨
(1)把一周长20厘米的正方形剪成2个完全一样的长方形,每个长方形的周长是10厘米。 ( )
(2)两个面积相等的三角形不一定能拼成一个平行四边形。 ( )
(3)把一个长方形木框拉成平行四边形,周长和面积都不变。 ( )
复习题
2.填一填
(1) 一根长6.28米的铁丝,围成一个正方形,面积是( )平方米;围成一个圆,面积是( )平方米。
(2) 用一根20厘米长的铁丝围成一个宽是4厘米的长方形,它的长是( )厘米,面积是( )平方厘米;如果围成一个正方形,它的面积是( )平方厘米;( )的面积大。
复习题
2.填一填
(3) 一个等腰三角形的底角是45度,他的顶角是( )度。
(4) 等腰三角形有( )条对称轴;等边三角形有( )条对称轴;长方形有( )条对称轴,正方形有( )条对称轴;圆形有( )条对称轴。
复习题
3.算一算
计算下面图形的面积。(单位:厘米)
10
45o
复习题
3.算一算
一块如图所示的直角梯形木板,工人把它锯成平
行四边形。如果锯出的直角三角形木板
的面积是24平方厘米,平行四边形木板
的面积是多少平方厘米?
18cm
15cm
复习题
3.算一算
(4) 在长为1.8米、宽为1.2米的纸板上,你能截出几个半径为30厘米的圆?并计算材料的利用率。
复习题
下面每个小方格的边长是1厘米,请在方格图上画一个平面图形.使它的面积是12平方厘米。你可以画哪些图形
你是怎样想的
4. 画一画
二、在“围一围”中复习“形”
(二)复习题设计
5. 画一画
(1)画出图①的全部对称轴。
(2)画出图②向下平移3格后的图形。
(3)画出图③绕A点顺时针方向旋转90度后的图形。
三、在“比一比”中复习“体”
(一)复习内容及方式。
在这一部分中,主要复习“四体”——长方体、正方体、圆柱、圆锥,并进一步辨认从不同方向看到的物体形状。
三、在“比一比”中复习“体”
(一)复习内容及方式。
1.特征之“比”。
2.表面积与体积之“比”。
3.体积和容积之“比”。
4.单位之“比”。
5. 从不同角度观察物体结果之“比”。
二、在“围一围”中复习“形”
(二)复习题设计
1.根据已知条件,求出下列形体的表面积和体积,填入下表。
形体名称 已知条件 表面积 体积
长方体 长2米,宽1.5米,高1.2米
正方体 棱长3分米
圆柱 底面半径4厘米,高3分米
圆锥 底面直径6厘米,高5厘米
二、在“围一围”中复习“形”
(二)复习题设计
2.从不同的方向观察下面左图,再说说右面三幅图分别表示从什么方向看到的。
二、在“围一围”中复习“形”
(二)复习题设计
3.填一填。
(1) 用一根24厘米长的铁丝焊成一个最大的立方体模型,它的表面积是( )平方厘米,体积是( )立方厘米。
(2) 一个底面积是正方形的长方体,底面周长是20厘米,高是12厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
二、在“围一围”中复习“形”
(二)复习题设计
3.填一填。
(3) 一个圆柱的底面直径和高都是10厘米,它的侧面积是( )平方厘米,表面积是( )平方厘米,体积是( )立方厘米。
(4) 一段圆柱形木头制成一个最大的圆锥,削去部分的体积是圆柱体积的( ),是圆锥体积的( )。
(一)掌握实际问题与几何图形之间的联系,具体问题具体分析,灵活运用所学知识
做一个底面周长是18.84厘米,高10厘米的圆柱体罐头盒,至少用多少铁皮?能装多少东西?在四周贴商标纸,用多少纸?
(一)掌握实际问题与几何图形之间的联系,具体问题具体分析,灵活运用所学知识
长方体鱼缸5个面,没有上面
烟囱只有侧面
游泳池
结合物体具体情况,到底求体积还是表面积。判断求那几个面的和。
(二)注重面积、体积公式的推导,紧抓图形间的关系,帮助学生理解记忆。
如:
(二)注重面积、体积公式的推导
(1)圆转化成长方形后什么发生改变,什么没变?
(2)关系
(3)题问:①周长增加多少
②给宽,求圆的面积
③给长方形长求圆面积
已知图中正方形的面积是3平方厘米,请求出圆的面积。
已知图中正方形的面积是3平方厘米,请求出圆的面积。
已知图中正方形的面积是3平方厘米,请求出圆的面积。
已知图中正方形的面积是3平方厘米,请求出圆的面积。
圆柱体
(1)什么变?什么不变?
(2)柱→长方体,表面积增加多少?
(3)圆柱体的侧面积62.8平方厘米,半径2厘米,求体积?
(三)注重动手操作
1、如量出所需数据
2、画出图形的对称轴,
3、尺规画图
(1) 会画长、正方形、圆形。
(2)会做平行四边形、三角形、梯形的高。
(四)注重开放性练习,提高学生思维能力
6厘米
12厘米
例:
6厘米
10厘米
6厘米
(五)注重培养学生良好的习惯
(1)培养审题(单位名称)
例:制作五个底面半径是2分米、高是8米的圆柱形烟囱,至少需要多少平米铁皮?
(五)注重培养学生良好的习惯
(2)培养建立表象的习惯,甚至可以画出草图抓关系,闭眼想,建立空间观念。
3
2
3
2
2
3
例:以直角三角形一条直角边为轴旋转出图形,体积最大是( )
空间与图形
“五线”——直线、射线、线段、垂线、平行线;
“五角”——锐角、直角、钝角、平角、周角。
直线
线段
射线
可以度量长度
向两端无限延长
向一端无限延长
2.任意画出两条直线
直线
线段
射线
平行
相交
可以度量长度
平行线
斜交
垂直
斜线
垂线
向兩端无限延长
向一端无限延长
在同一平面內
兩条直线位置
3.用两条射线画角
直线
线段
射线
平行
相交
可以度量长度
角
直角
锐角
钝角
平角
周角
平行线
斜交
垂直
斜线
垂线
向两端无限延长
向一端无限延长
在同一平面內
兩条直线位置
1.火眼金睛辨对错。
(1)一条射线长10厘米。 ( )
(2)过两点只能画出一条直线。 ( )
(3)互相垂直的两条直线相交成4个角,4个角都是直角。 ( )
(4)不相交的两条直线叫平行线。 ( )
(5)大于90。的角是钝角。 ( )
(6)平角就是一条直线。 ( )
(7)用一个10倍的放大镜看一个10度的角就是100度。
( )
(8)小明画了一条10厘米长的直线。 ( )
(9)过直线外一点只能画一条直线与这条直线平行。
( )
2.巧画图形我能行。
(1) 清你用量角器画一个135度的角。你还能用其他方法画135度的角吗 请你把方法写出来。
2.巧画图形我能行。
(2)按要求画简易地图。以体操广场为观测点,完成右面的街区图,标出下面题中的地点和道路名。(比例尺:1:100000)
北
仿古路
体操场
① 汽车站在体操广场正北3000米处。
② 实验小学在体操广场西偏南40度的2000米处。
③ 便民超市在体操广场正东1500米处。
④ 318国道经过便民超市门前,与仿古路平行。
3.千变万化找联系。
(1) 直角的 是( )度,是( )角;周角
的 是( )度,是( )角;直角的( )
倍是平角。
1
5
4
9
(2) 计算角2,角3的度数。
1
2
3
450
在这一部分中,主要复习“七形”——长方形、正方形、平行四边形、三角形、梯形、圆、扇形(选学内容) 。
平面图形
三角形
四边形
平行四边形
长方形
正方形
梯形
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
正三角形
任意梯形
直角梯形
等腰梯形
圆
扇形
两组对边分别平行
只有一组对边平行
四个直角
四边相等
按角分
按边分
已学平面图形
不封闭的平面图形(“五线” 和“五角” )
封闭的平面图形(“七形”)
复习题
1.辨一辨
(1)把一周长20厘米的正方形剪成2个完全一样的长方形,每个长方形的周长是10厘米。 ( )
(2)两个面积相等的三角形不一定能拼成一个平行四边形。 ( )
(3)把一个长方形木框拉成平行四边形,周长和面积都不变。 ( )
复习题
2.填一填
(1) 一根长6.28米的铁丝,围成一个正方形,面积是( )平方米;围成一个圆,面积是( )平方米。
(2) 用一根20厘米长的铁丝围成一个宽是4厘米的长方形,它的长是( )厘米,面积是( )平方厘米;如果围成一个正方形,它的面积是( )平方厘米;( )的面积大。
复习题
2.填一填
(3) 一个等腰三角形的底角是45度,他的顶角是( )度。
(4) 等腰三角形有( )条对称轴;等边三角形有( )条对称轴;长方形有( )条对称轴,正方形有( )条对称轴;圆形有( )条对称轴。
复习题
3.算一算
计算下面图形的面积。(单位:厘米)
10
45o
复习题
3.算一算
一块如图所示的直角梯形木板,工人把它锯成平
行四边形。如果锯出的直角三角形木板
的面积是24平方厘米,平行四边形木板
的面积是多少平方厘米?
18cm
15cm
复习题
3.算一算
(4) 在长为1.8米、宽为1.2米的纸板上,你能截出几个半径为30厘米的圆?并计算材料的利用率。
复习题
下面每个小方格的边长是1厘米,请在方格图上画一个平面图形.使它的面积是12平方厘米。你可以画哪些图形
你是怎样想的
4. 画一画
二、在“围一围”中复习“形”
(二)复习题设计
5. 画一画
(1)画出图①的全部对称轴。
(2)画出图②向下平移3格后的图形。
(3)画出图③绕A点顺时针方向旋转90度后的图形。
三、在“比一比”中复习“体”
(一)复习内容及方式。
在这一部分中,主要复习“四体”——长方体、正方体、圆柱、圆锥,并进一步辨认从不同方向看到的物体形状。
三、在“比一比”中复习“体”
(一)复习内容及方式。
1.特征之“比”。
2.表面积与体积之“比”。
3.体积和容积之“比”。
4.单位之“比”。
5. 从不同角度观察物体结果之“比”。
二、在“围一围”中复习“形”
(二)复习题设计
1.根据已知条件,求出下列形体的表面积和体积,填入下表。
形体名称 已知条件 表面积 体积
长方体 长2米,宽1.5米,高1.2米
正方体 棱长3分米
圆柱 底面半径4厘米,高3分米
圆锥 底面直径6厘米,高5厘米
二、在“围一围”中复习“形”
(二)复习题设计
2.从不同的方向观察下面左图,再说说右面三幅图分别表示从什么方向看到的。
二、在“围一围”中复习“形”
(二)复习题设计
3.填一填。
(1) 用一根24厘米长的铁丝焊成一个最大的立方体模型,它的表面积是( )平方厘米,体积是( )立方厘米。
(2) 一个底面积是正方形的长方体,底面周长是20厘米,高是12厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
二、在“围一围”中复习“形”
(二)复习题设计
3.填一填。
(3) 一个圆柱的底面直径和高都是10厘米,它的侧面积是( )平方厘米,表面积是( )平方厘米,体积是( )立方厘米。
(4) 一段圆柱形木头制成一个最大的圆锥,削去部分的体积是圆柱体积的( ),是圆锥体积的( )。
(一)掌握实际问题与几何图形之间的联系,具体问题具体分析,灵活运用所学知识
做一个底面周长是18.84厘米,高10厘米的圆柱体罐头盒,至少用多少铁皮?能装多少东西?在四周贴商标纸,用多少纸?
(一)掌握实际问题与几何图形之间的联系,具体问题具体分析,灵活运用所学知识
长方体鱼缸5个面,没有上面
烟囱只有侧面
游泳池
结合物体具体情况,到底求体积还是表面积。判断求那几个面的和。
(二)注重面积、体积公式的推导,紧抓图形间的关系,帮助学生理解记忆。
如:
(二)注重面积、体积公式的推导
(1)圆转化成长方形后什么发生改变,什么没变?
(2)关系
(3)题问:①周长增加多少
②给宽,求圆的面积
③给长方形长求圆面积
已知图中正方形的面积是3平方厘米,请求出圆的面积。
已知图中正方形的面积是3平方厘米,请求出圆的面积。
已知图中正方形的面积是3平方厘米,请求出圆的面积。
已知图中正方形的面积是3平方厘米,请求出圆的面积。
圆柱体
(1)什么变?什么不变?
(2)柱→长方体,表面积增加多少?
(3)圆柱体的侧面积62.8平方厘米,半径2厘米,求体积?
(三)注重动手操作
1、如量出所需数据
2、画出图形的对称轴,
3、尺规画图
(1) 会画长、正方形、圆形。
(2)会做平行四边形、三角形、梯形的高。
(四)注重开放性练习,提高学生思维能力
6厘米
12厘米
例:
6厘米
10厘米
6厘米
(五)注重培养学生良好的习惯
(1)培养审题(单位名称)
例:制作五个底面半径是2分米、高是8米的圆柱形烟囱,至少需要多少平米铁皮?
(五)注重培养学生良好的习惯
(2)培养建立表象的习惯,甚至可以画出草图抓关系,闭眼想,建立空间观念。
3
2
3
2
2
3
例:以直角三角形一条直角边为轴旋转出图形,体积最大是( )
