高中物理 人教版(2019) 必修 第二册 7.2万有引力定律 学案(有解析)
文档属性
| 名称 | 高中物理 人教版(2019) 必修 第二册 7.2万有引力定律 学案(有解析) |  | |
| 格式 | zip | ||
| 文件大小 | 445.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-14 10:52:09 | ||
图片预览


文档简介
7.2万有引力定律
二、万有引力定律
1.内容
(1)自然界中任何两个物体都相互吸引。
(2)引力的方向在它们的连线上。
(3)引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比。
2.表达式
F=G,其中G为引力常量,G=6.67×10-11 N·m2/kg2,由卡文迪什扭秤实验测定。
3.适用条件
(1)两个质点之间的相互作用。当两个物体间的距离远大于物体本身的大小时物体可视为质点。
(2)对质量分布均匀的球体,r为两球心间的距离。
(3)一个质量分布均匀的球体和球外一个质点间的万有引力的计算,r为质点到球心间的距离。
1.行星绕太阳的运动通常按圆轨道处理。
2.由开普勒第二定律可得v1·Δt·r1=v2·Δt·r2,解得=,即行星在两个位置的速度之比与到太阳的距离成反比,近日点速度最大,远日点速度最小。
3.开普勒第三定律=k中,k值只与中心天体的质量有关,不同的中心天体k值不同。该定律只能用在同一中心天体的两星体之间。
7.2
一、填空题
1.行星与太阳间的引力
(1)太阳对行星的引力:太阳对行星的引力,与行星的质量成 _______,与行星和太阳间距离的二次方成 ___,即。
(2)行星对太阳的引力:在引力的存在与性质上,太阳与行星的地位完全相当,因此行星对太阳的引力和太阳对行星的引力规律相同,即。
(3)太阳与行星间的引力:根据牛顿第三定律F=F′,所以有,写成等式就是。
2.月—地检验
(1)检验目的:检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的引力是否为_____的力。
(2)检验方法:
a.假设地球与月球间的作用力和太阳与行星间的作用力是同一种力,它们的表达式也应该满足。
b.根据牛顿第二定律,月球绕地球做圆周运动的向心加速度(式中m地是地球质量,r是地球中心与月球中心的距离)。
c.假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度(式中m地是地球的质量,R是地球中心与苹果间的距离)。
d.,由于r≈60R,所以。
(3)验证:
a.苹果自由落体加速度a苹=g=9.8 m/s2。
b.月球中心到地球中心的距离r=3.8×108 m。
月球公转周期T=27.3 d≈2.36×106 s
则a月=≈_______m/s2(保留两位有效数字)
______(数值)≈(比例)。
(4)结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从_____的规律。
3.万有引力定律
(1)内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量____________成正比、与它们之间____________成反比。
(2)表达式:F=G,其中G叫作引力常量。
4.引力常量
牛顿得出了万有引力与物体质量及它们之间距离的关系,但没有测出引力常量G的值。
英国物理学家_______通过实验推算出引力常量G的值。通常情况下取G=________N·m2/kg2。
5.判断下列说法的正误。
(1)万有引力不仅存在于天体之间,也存在于普通物体之间。( )
(2)牛顿发现了万有引力定律,并测出了引力常量。( )
(3)质量一定的两个物体,若距离无限小,它们间的万有引力趋于无限大。( )
(4)由于太阳质量大,太阳对行星的引力大于行星对太阳的引力。( )
6.两个质量都是1 kg的物体(可看成质点),相距1 m时,两物体间的万有引力F=________ N,一个物体的重力F′=________ N,万有引力F与重力F′的比值为________.(已知引力常量G=6.67×10-11N·m2/kg2,重力加速度g=10 m/s2).
二、单选题
7.关于行星运动定律和万有引力定律的建立过程,下列说法正确的是( )
A.牛顿发现了万有引力定律,并且测得引力常量的数值
B.第谷接受了哥白尼日心说的观点,并根据开普勒对行星运动观察记录的数据,应用严密的数学运算和椭圆轨道假说,得出了开普勒行星运动定律
C.牛顿通过比较月球公转的向心加速度和地球赤道上物体随地球自转的向心加速度,对万有引力定律进行了“月地检验”
D.卡文迪许在实验室里通过几个铅球之间万有引力的测量,得出了引力常量的数值
8.物理学领域中具有普适性的一些常量,对物理学的发展有很大作用,引力常量G就是其中之一1798年,卡文迪什首次利用如图所示的装置,比较精确地测量出了引力常量。下列说法错误的是( )
A.引力常量不易测量的一个重要原因就是地面上普通物体间的引力太微小
B.月球上的引力常量等于地球上的引力常量
C.这个实验装置巧妙地利用放大原理,提高了测量精度
D.引力常量G的大小与两物体质量的乘积成反比,与两物体间距离的平方成正比
9.下列说法中正确的是( )
A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力
B.根据表达式可知,当r趋近于零时,万有引力趋近于无穷大
C.牛顿发现了万有引力定律,并测出了引力常量G
D.开普勒第三定律得出的表达式,其中k是一个与中心天体无关的常量
10.两个质量均匀的球体相距较远的距离,它们之间的万有引力为。若它们的质量不变、距离减小为原来的倍,则它们间的万有引力为( )
A. B.
C. D.
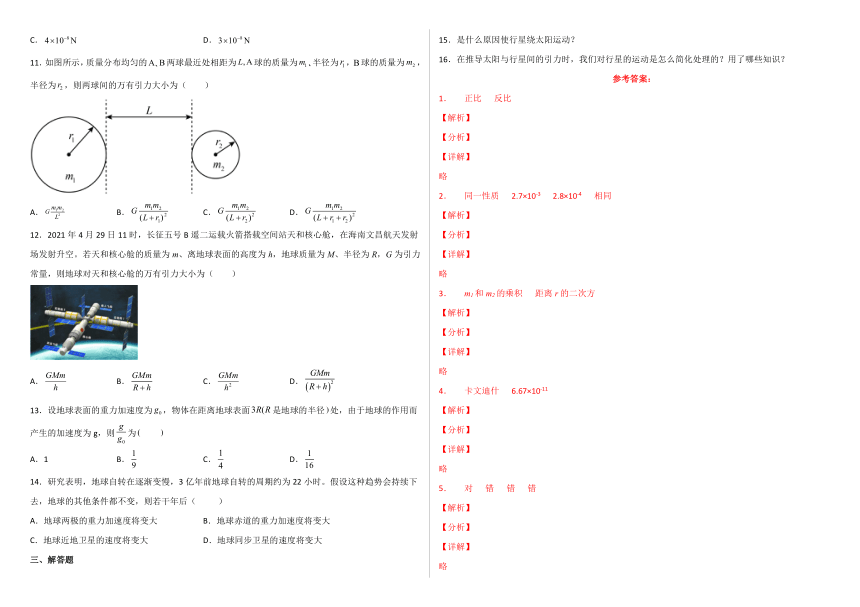
11.如图所示,质量分布均匀的两球最近处相距为球的质量为 半径为,球的质量为,半径为,则两球间的万有引力大小为( )
A. B. C. D.
12.2021年4月29日11时,长征五号B遥二运载火箭搭载空间站天和核心舱,在海南文昌航天发射场发射升空。若天和核心舱的质量为m、离地球表面的高度为h,地球质量为M、半径为R,G为引力常量,则地球对天和核心舱的万有引力大小为( )
A. B. C. D.
13.设地球表面的重力加速度为,物体在距离地球表面是地球的半径处,由于地球的作用而产生的加速度为g,则为
A.1 B. C. D.
14.研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时。假设这种趋势会持续下去,地球的其他条件都不变,则若干年后( )
A.地球两极的重力加速度将变大 B.地球赤道的重力加速度将变大
C.地球近地卫星的速度将变大 D.地球同步卫星的速度将变大
三、解答题
15.是什么原因使行星绕太阳运动?
16.在推导太阳与行星间的引力时,我们对行星的运动是怎么简化处理的?用了哪些知识?
参考答案:
1. 正比 反比
【解析】
【分析】
【详解】
略
2. 同一性质 2.7×10-3 2.8×10-4 相同
【解析】
【分析】
【详解】
略
3. m1和m2的乘积 距离r的二次方
【解析】
【分析】
【详解】
略
4. 卡文迪什 6.67×10-11
【解析】
【分析】
【详解】
略
5. 对 错 错 错
【解析】
【分析】
【详解】
略
6. 6.67×10-11 10 6.67×10-12
【解析】
【详解】
根据万有引力公式:,重力为:,万有引力F与重力F′的比值为:.
7.D
【解析】
【详解】
A、D项:牛顿发现了万有引力定律之后,第一次通过实验比较准确地测出万有引力常量的科学家是卡文迪许,故A错误,D正确;
B项:开普勒对第谷的行星运动观察记录的数据做了多年的研究,最终得出了行星运行三大定律,故B错误;
C项:牛顿通过比较月球公转的周期,根据万有引力充当向心力,对万有引力定律进行了“月地检验”,故C错误.
8.D
【解析】
【分析】
【详解】
A.引力常量不易测量的一个重要原因就是地面上普通物体间的引力太微小,选项A正确,不符合题意;
B.引力常数是固定不变的量,与在月球上还是地球上无关,选项B正确,不符合题意;
C.这个实验装置巧妙地利用放大原理,提高了测量精度,选项C正确,不符合题意;
D.引力常量G的大小为定值,与两物体质量的乘积以及两物体间距离的平方无关,选项D错误,符合题意。
故选D。
9.A
【解析】
【分析】
【详解】
A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力,选项A正确;
B.根据表达式
可知,当r趋近于零时,万有引力定律不再适用,选项B错误;
C.牛顿发现了万有引力定律,卡文迪许测出了引力常量G,选项C错误;
D.开普勒第三定律得出的表达式
其中k是一个与中心天体有关的常量,选项D错误。
故选A。
10.C
【解析】
【详解】
根据万有引力公式
距离减小为原来的一半,则力变为原来的4倍,即
故选C。
11.D
【解析】
【分析】
【详解】
两球球心间的距离为
则两球间的万有引力
故选D。
12.D
【解析】
【详解】
卫星到地心的距离为
r=R+h
地球对卫星万有引力的大小为
故选D。
13.D
【解析】
【分析】
【详解】
根据地球表面重力与万有引力近似相等
有地球表面处的重力加速度
离地球表面3R,即离地心距离4R处,根据牛顿第二定律
即
故ABC错误,D正确.
故选D。
14.B
【解析】
【详解】
A.在两极由公式
得
所以两极的重力加速度不变,故A错误;
B.在赤道上有
由于周期变大,赤道上的重力加速度变大,故B正确;
C.由公式
得
所以地球近地卫星的速度不变,故C错误;
D.由公式
得
现在同步卫星的周期变大,则知,其轨道半径r增大,则线速度v减小,故D错误。
故选B。
15.太阳对行星的引力使行星绕太阳运动。
【解析】
略
16.将行星绕太阳的椭圆运动看成匀速圆周运动。在推导过程中,用到了向心力公式、开普勒第三定律及牛顿运动定律。
【解析】
略
二、万有引力定律
1.内容
(1)自然界中任何两个物体都相互吸引。
(2)引力的方向在它们的连线上。
(3)引力的大小与物体的质量m1和m2的乘积成正比、与它们之间距离r的二次方成反比。
2.表达式
F=G,其中G为引力常量,G=6.67×10-11 N·m2/kg2,由卡文迪什扭秤实验测定。
3.适用条件
(1)两个质点之间的相互作用。当两个物体间的距离远大于物体本身的大小时物体可视为质点。
(2)对质量分布均匀的球体,r为两球心间的距离。
(3)一个质量分布均匀的球体和球外一个质点间的万有引力的计算,r为质点到球心间的距离。
1.行星绕太阳的运动通常按圆轨道处理。
2.由开普勒第二定律可得v1·Δt·r1=v2·Δt·r2,解得=,即行星在两个位置的速度之比与到太阳的距离成反比,近日点速度最大,远日点速度最小。
3.开普勒第三定律=k中,k值只与中心天体的质量有关,不同的中心天体k值不同。该定律只能用在同一中心天体的两星体之间。
7.2
一、填空题
1.行星与太阳间的引力
(1)太阳对行星的引力:太阳对行星的引力,与行星的质量成 _______,与行星和太阳间距离的二次方成 ___,即。
(2)行星对太阳的引力:在引力的存在与性质上,太阳与行星的地位完全相当,因此行星对太阳的引力和太阳对行星的引力规律相同,即。
(3)太阳与行星间的引力:根据牛顿第三定律F=F′,所以有,写成等式就是。
2.月—地检验
(1)检验目的:检验地球绕太阳运动、月球绕地球运动的力与地球对树上苹果的引力是否为_____的力。
(2)检验方法:
a.假设地球与月球间的作用力和太阳与行星间的作用力是同一种力,它们的表达式也应该满足。
b.根据牛顿第二定律,月球绕地球做圆周运动的向心加速度(式中m地是地球质量,r是地球中心与月球中心的距离)。
c.假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度(式中m地是地球的质量,R是地球中心与苹果间的距离)。
d.,由于r≈60R,所以。
(3)验证:
a.苹果自由落体加速度a苹=g=9.8 m/s2。
b.月球中心到地球中心的距离r=3.8×108 m。
月球公转周期T=27.3 d≈2.36×106 s
则a月=≈_______m/s2(保留两位有效数字)
______(数值)≈(比例)。
(4)结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从_____的规律。
3.万有引力定律
(1)内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量____________成正比、与它们之间____________成反比。
(2)表达式:F=G,其中G叫作引力常量。
4.引力常量
牛顿得出了万有引力与物体质量及它们之间距离的关系,但没有测出引力常量G的值。
英国物理学家_______通过实验推算出引力常量G的值。通常情况下取G=________N·m2/kg2。
5.判断下列说法的正误。
(1)万有引力不仅存在于天体之间,也存在于普通物体之间。( )
(2)牛顿发现了万有引力定律,并测出了引力常量。( )
(3)质量一定的两个物体,若距离无限小,它们间的万有引力趋于无限大。( )
(4)由于太阳质量大,太阳对行星的引力大于行星对太阳的引力。( )
6.两个质量都是1 kg的物体(可看成质点),相距1 m时,两物体间的万有引力F=________ N,一个物体的重力F′=________ N,万有引力F与重力F′的比值为________.(已知引力常量G=6.67×10-11N·m2/kg2,重力加速度g=10 m/s2).
二、单选题
7.关于行星运动定律和万有引力定律的建立过程,下列说法正确的是( )
A.牛顿发现了万有引力定律,并且测得引力常量的数值
B.第谷接受了哥白尼日心说的观点,并根据开普勒对行星运动观察记录的数据,应用严密的数学运算和椭圆轨道假说,得出了开普勒行星运动定律
C.牛顿通过比较月球公转的向心加速度和地球赤道上物体随地球自转的向心加速度,对万有引力定律进行了“月地检验”
D.卡文迪许在实验室里通过几个铅球之间万有引力的测量,得出了引力常量的数值
8.物理学领域中具有普适性的一些常量,对物理学的发展有很大作用,引力常量G就是其中之一1798年,卡文迪什首次利用如图所示的装置,比较精确地测量出了引力常量。下列说法错误的是( )
A.引力常量不易测量的一个重要原因就是地面上普通物体间的引力太微小
B.月球上的引力常量等于地球上的引力常量
C.这个实验装置巧妙地利用放大原理,提高了测量精度
D.引力常量G的大小与两物体质量的乘积成反比,与两物体间距离的平方成正比
9.下列说法中正确的是( )
A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力
B.根据表达式可知,当r趋近于零时,万有引力趋近于无穷大
C.牛顿发现了万有引力定律,并测出了引力常量G
D.开普勒第三定律得出的表达式,其中k是一个与中心天体无关的常量
10.两个质量均匀的球体相距较远的距离,它们之间的万有引力为。若它们的质量不变、距离减小为原来的倍,则它们间的万有引力为( )
A. B.
C. D.
11.如图所示,质量分布均匀的两球最近处相距为球的质量为 半径为,球的质量为,半径为,则两球间的万有引力大小为( )
A. B. C. D.
12.2021年4月29日11时,长征五号B遥二运载火箭搭载空间站天和核心舱,在海南文昌航天发射场发射升空。若天和核心舱的质量为m、离地球表面的高度为h,地球质量为M、半径为R,G为引力常量,则地球对天和核心舱的万有引力大小为( )
A. B. C. D.
13.设地球表面的重力加速度为,物体在距离地球表面是地球的半径处,由于地球的作用而产生的加速度为g,则为
A.1 B. C. D.
14.研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时。假设这种趋势会持续下去,地球的其他条件都不变,则若干年后( )
A.地球两极的重力加速度将变大 B.地球赤道的重力加速度将变大
C.地球近地卫星的速度将变大 D.地球同步卫星的速度将变大
三、解答题
15.是什么原因使行星绕太阳运动?
16.在推导太阳与行星间的引力时,我们对行星的运动是怎么简化处理的?用了哪些知识?
参考答案:
1. 正比 反比
【解析】
【分析】
【详解】
略
2. 同一性质 2.7×10-3 2.8×10-4 相同
【解析】
【分析】
【详解】
略
3. m1和m2的乘积 距离r的二次方
【解析】
【分析】
【详解】
略
4. 卡文迪什 6.67×10-11
【解析】
【分析】
【详解】
略
5. 对 错 错 错
【解析】
【分析】
【详解】
略
6. 6.67×10-11 10 6.67×10-12
【解析】
【详解】
根据万有引力公式:,重力为:,万有引力F与重力F′的比值为:.
7.D
【解析】
【详解】
A、D项:牛顿发现了万有引力定律之后,第一次通过实验比较准确地测出万有引力常量的科学家是卡文迪许,故A错误,D正确;
B项:开普勒对第谷的行星运动观察记录的数据做了多年的研究,最终得出了行星运行三大定律,故B错误;
C项:牛顿通过比较月球公转的周期,根据万有引力充当向心力,对万有引力定律进行了“月地检验”,故C错误.
8.D
【解析】
【分析】
【详解】
A.引力常量不易测量的一个重要原因就是地面上普通物体间的引力太微小,选项A正确,不符合题意;
B.引力常数是固定不变的量,与在月球上还是地球上无关,选项B正确,不符合题意;
C.这个实验装置巧妙地利用放大原理,提高了测量精度,选项C正确,不符合题意;
D.引力常量G的大小为定值,与两物体质量的乘积以及两物体间距离的平方无关,选项D错误,符合题意。
故选D。
9.A
【解析】
【分析】
【详解】
A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力,选项A正确;
B.根据表达式
可知,当r趋近于零时,万有引力定律不再适用,选项B错误;
C.牛顿发现了万有引力定律,卡文迪许测出了引力常量G,选项C错误;
D.开普勒第三定律得出的表达式
其中k是一个与中心天体有关的常量,选项D错误。
故选A。
10.C
【解析】
【详解】
根据万有引力公式
距离减小为原来的一半,则力变为原来的4倍,即
故选C。
11.D
【解析】
【分析】
【详解】
两球球心间的距离为
则两球间的万有引力
故选D。
12.D
【解析】
【详解】
卫星到地心的距离为
r=R+h
地球对卫星万有引力的大小为
故选D。
13.D
【解析】
【分析】
【详解】
根据地球表面重力与万有引力近似相等
有地球表面处的重力加速度
离地球表面3R,即离地心距离4R处,根据牛顿第二定律
即
故ABC错误,D正确.
故选D。
14.B
【解析】
【详解】
A.在两极由公式
得
所以两极的重力加速度不变,故A错误;
B.在赤道上有
由于周期变大,赤道上的重力加速度变大,故B正确;
C.由公式
得
所以地球近地卫星的速度不变,故C错误;
D.由公式
得
现在同步卫星的周期变大,则知,其轨道半径r增大,则线速度v减小,故D错误。
故选B。
15.太阳对行星的引力使行星绕太阳运动。
【解析】
略
16.将行星绕太阳的椭圆运动看成匀速圆周运动。在推导过程中,用到了向心力公式、开普勒第三定律及牛顿运动定律。
【解析】
略
