7.4 由三角函数值求锐角同步练习(含答案)
文档属性
| 名称 | 7.4 由三角函数值求锐角同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 107.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-13 17:50:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
7.4由三角函数值求锐角 苏科版初中数学九年级下册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共6小题,共18分)
一个直角三角形有两条边长分别为,,则较小的锐角约为( )
A. B. C. 或 D.
在中,,,运用计算器计算的度数约为精确到( )
A. B. C. D.
用计算器求、、、、、、、的值,研究的值随锐角变化的规律,根据这个规律判断:若,则( )
A. B. C. D.
已知,,,则,,的大小为( )
A. B.
C. D.
如图,轮船沿正南方向以海里时的速度匀速航行,在处观测到灯塔在西偏南方向上,航行小时后到达处,观测灯塔在西偏南方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为由科学计算器得到,,,( )
A. 海里 B. 海里 C. 海里 D. 海里
在中,,,下列四个选项,正确的是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共1小题,共3分)
已知一条长度为米的斜坡两端的垂直高度差为米,那么该斜坡的坡角度数约为 结果精确到
三、解答题(本大题共7小题,共56分)
在中,,,求的长精确到.
已知一个等腰三角形的腰长为,底边长为求顶角的大小精确到
一辆汽车沿着一山坡行驶了,其竖直高度上升了求山坡与水平面所成的锐角的大小精确到
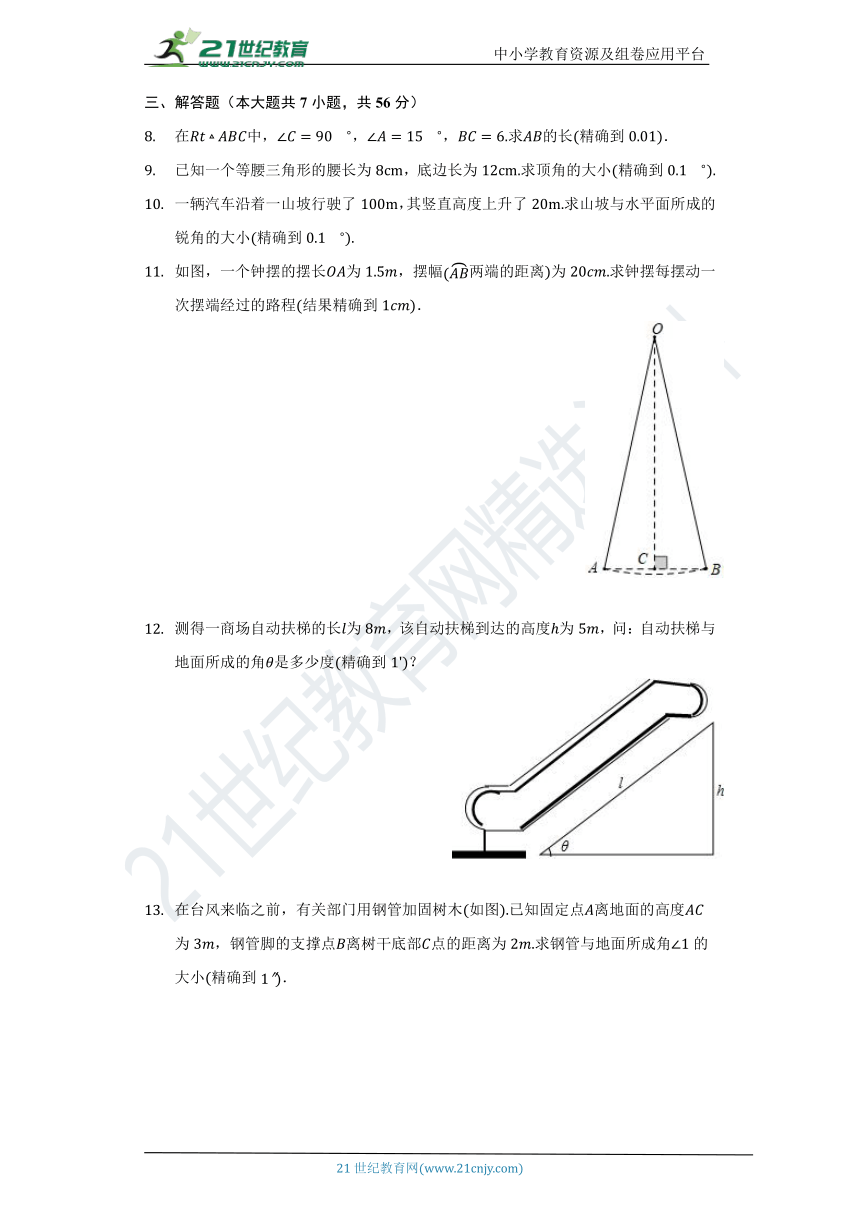
如图,一个钟摆的摆长为,摆幅两端的距离为求钟摆每摆动一次摆端经过的路程结果精确到.
测得一商场自动扶梯的长为,该自动扶梯到达的高度为,问:自动扶梯与地面所成的角是多少度精确到?
在台风来临之前,有关部门用钢管加固树木如图已知固定点离地面的高度为,钢管脚的支撑点离树干底部点的距离为求钢管与地面所成角的大小精确到.
如图,河两岸,互相平行,小明和小慧要测量河的宽度,小明在点测得对岸河边的树正好在他的正北方向,小慧站在小明正东方向的点,测得,两点之间的距离是根据上述测量数据,你能求出河的宽度吗精确到?
答案和解析
1.【答案】
【解析】
【分析】
本题考查本题考查了勾股定理、求三角函数值、利用计算器求反三角函数、分情况讨论;
此题分情况计算:若、是直角边,利用勾股定理可求斜边,从而可求较小锐角的正弦值,再利用计算器可求角;是斜边,利用勾股定理可求较小边,从而求出其所对角的正弦值,再利用计算器可求角.
【解答】
解:若、是两直角边长;
两直角边长分别为、,
斜边长为,
较小的锐角所对的直角边长为,
则其正弦值为,
利用计算器求得较小的锐角约为.
若斜边长为,则另一边长为,则较小边长为,
较小的锐角的正弦值为,
利用计算器求得较小的锐角约为
2.【答案】
【解析】
【分析】
本题考查在直角三角形中解题,根据角的正弦值求出三角形的角度.根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后求出.
【解答】
解:::,
设,,
由勾股定理知,
,
运用计算器得,.
故选B.
3.【答案】
【解析】解:,,,,,,,,
的值随锐角的增大而增大,
,
.
故选A
4.【答案】
【解析】解:由科学计算器可得,,
,故选D.
5.【答案】
【解析】
【分析】
此题主要考查了方向角问题,熟练应用锐角三角函数关系是解题关键.过点作于点,则若该船继续向南航行至离灯塔距离最近的位置为的长度,利用锐角三角函数关系进行求解即可.
【解答】
解:如图,过点作于点,
海里,
,,
,
,
,
,
,
海里,
,
,
海里
故选:.
6.【答案】
【解析】解:如图,,,,
,
选项,原式,故该选项不符合题意;
选项,原式,故该选项不符合题意;
选项,原式,故该选项符合题意;
选项,原式,故该选项不符合题意;
故选:.
根据勾股定理求出的长,根据锐角三角函数的定义求值即可得出答案.
本题考查了勾股定理,锐角三角函数,牢记锐角三角函数的定义是解题的关键.
7.【答案】
【解析】略
8.【答案】解:由题意知,,
则.
用计算器计算,得.
【解析】见答案.
9.【答案】略
【解析】略
10.【答案】略
【解析】略
11.【答案】解:过点作于,如图,则,
在中,,
,
,
,
的长度,
即钟摆每摆动一次摆端经过的路程约为.
【解析】过点作于,如图,根据垂径定理得到,再利用正弦的定义求出,则,然后根据弧长公式计算的长度即可.
本题考查了弧长公式:弧长为,圆心角度数为,圆的半径为也考查了垂径定理.
12.【答案】解:自动扶梯的长为,该自动扶梯到达的高度为,
,
.
【解析】利用三角函数的定义得出,进而求解即可.
本题考查了三角函数的定义问题,正确理解三角函数的定义是关键.
13.【答案】解:固定点离地面的高度为,钢管脚的支撑点离树干底部点的距离为,
,
;
答:钢管与地面所成角的度数是.
【解析】根据题意得出,,再根据,代入计算即可求出的度数.
此题考查了三角函数定义,关键是根据正切的定义得出,把实际问题转化为数学问题加以计算.
14.【答案】解:根据题意得:,,,
在中,
.
、两点之间的距离为,
即河的宽度为.
【解析】由题意可知,,,然后在中,利用正切函数,即可求得、两点之间的距离即河的宽度.
此题考查三角函数定义.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
7.4由三角函数值求锐角 苏科版初中数学九年级下册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共6小题,共18分)
一个直角三角形有两条边长分别为,,则较小的锐角约为( )
A. B. C. 或 D.
在中,,,运用计算器计算的度数约为精确到( )
A. B. C. D.
用计算器求、、、、、、、的值,研究的值随锐角变化的规律,根据这个规律判断:若,则( )
A. B. C. D.
已知,,,则,,的大小为( )
A. B.
C. D.
如图,轮船沿正南方向以海里时的速度匀速航行,在处观测到灯塔在西偏南方向上,航行小时后到达处,观测灯塔在西偏南方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为由科学计算器得到,,,( )
A. 海里 B. 海里 C. 海里 D. 海里
在中,,,下列四个选项,正确的是( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共1小题,共3分)
已知一条长度为米的斜坡两端的垂直高度差为米,那么该斜坡的坡角度数约为 结果精确到
三、解答题(本大题共7小题,共56分)
在中,,,求的长精确到.
已知一个等腰三角形的腰长为,底边长为求顶角的大小精确到
一辆汽车沿着一山坡行驶了,其竖直高度上升了求山坡与水平面所成的锐角的大小精确到
如图,一个钟摆的摆长为,摆幅两端的距离为求钟摆每摆动一次摆端经过的路程结果精确到.
测得一商场自动扶梯的长为,该自动扶梯到达的高度为,问:自动扶梯与地面所成的角是多少度精确到?
在台风来临之前,有关部门用钢管加固树木如图已知固定点离地面的高度为,钢管脚的支撑点离树干底部点的距离为求钢管与地面所成角的大小精确到.
如图,河两岸,互相平行,小明和小慧要测量河的宽度,小明在点测得对岸河边的树正好在他的正北方向,小慧站在小明正东方向的点,测得,两点之间的距离是根据上述测量数据,你能求出河的宽度吗精确到?
答案和解析
1.【答案】
【解析】
【分析】
本题考查本题考查了勾股定理、求三角函数值、利用计算器求反三角函数、分情况讨论;
此题分情况计算:若、是直角边,利用勾股定理可求斜边,从而可求较小锐角的正弦值,再利用计算器可求角;是斜边,利用勾股定理可求较小边,从而求出其所对角的正弦值,再利用计算器可求角.
【解答】
解:若、是两直角边长;
两直角边长分别为、,
斜边长为,
较小的锐角所对的直角边长为,
则其正弦值为,
利用计算器求得较小的锐角约为.
若斜边长为,则另一边长为,则较小边长为,
较小的锐角的正弦值为,
利用计算器求得较小的锐角约为
2.【答案】
【解析】
【分析】
本题考查在直角三角形中解题,根据角的正弦值求出三角形的角度.根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长,然后求出.
【解答】
解:::,
设,,
由勾股定理知,
,
运用计算器得,.
故选B.
3.【答案】
【解析】解:,,,,,,,,
的值随锐角的增大而增大,
,
.
故选A
4.【答案】
【解析】解:由科学计算器可得,,
,故选D.
5.【答案】
【解析】
【分析】
此题主要考查了方向角问题,熟练应用锐角三角函数关系是解题关键.过点作于点,则若该船继续向南航行至离灯塔距离最近的位置为的长度,利用锐角三角函数关系进行求解即可.
【解答】
解:如图,过点作于点,
海里,
,,
,
,
,
,
,
海里,
,
,
海里
故选:.
6.【答案】
【解析】解:如图,,,,
,
选项,原式,故该选项不符合题意;
选项,原式,故该选项不符合题意;
选项,原式,故该选项符合题意;
选项,原式,故该选项不符合题意;
故选:.
根据勾股定理求出的长,根据锐角三角函数的定义求值即可得出答案.
本题考查了勾股定理,锐角三角函数,牢记锐角三角函数的定义是解题的关键.
7.【答案】
【解析】略
8.【答案】解:由题意知,,
则.
用计算器计算,得.
【解析】见答案.
9.【答案】略
【解析】略
10.【答案】略
【解析】略
11.【答案】解:过点作于,如图,则,
在中,,
,
,
,
的长度,
即钟摆每摆动一次摆端经过的路程约为.
【解析】过点作于,如图,根据垂径定理得到,再利用正弦的定义求出,则,然后根据弧长公式计算的长度即可.
本题考查了弧长公式:弧长为,圆心角度数为,圆的半径为也考查了垂径定理.
12.【答案】解:自动扶梯的长为,该自动扶梯到达的高度为,
,
.
【解析】利用三角函数的定义得出,进而求解即可.
本题考查了三角函数的定义问题,正确理解三角函数的定义是关键.
13.【答案】解:固定点离地面的高度为,钢管脚的支撑点离树干底部点的距离为,
,
;
答:钢管与地面所成角的度数是.
【解析】根据题意得出,,再根据,代入计算即可求出的度数.
此题考查了三角函数定义,关键是根据正切的定义得出,把实际问题转化为数学问题加以计算.
14.【答案】解:根据题意得:,,,
在中,
.
、两点之间的距离为,
即河的宽度为.
【解析】由题意可知,,,然后在中,利用正切函数,即可求得、两点之间的距离即河的宽度.
此题考查三角函数定义.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
