8.6 收取多少保险费才合理 同步练习(含答案)
文档属性
| 名称 | 8.6 收取多少保险费才合理 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 284.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-13 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
8.6收取多少保险费才合理苏科版初中数学九年级下册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
某地旅游管理部门在某景区随机调查了名游客,其中有名游客对该景区的服务表示满意对于此次调查,下列说法正确的是( )
A. 若随机调查名游客,则该游客表示满意的概率约为
B. 若随机调查名游客,则一定有名游客表示满意
C. 在所有到该景区旅游的游客中,只有名游客表示满意
D. 本次调查采用的方式是普查
抛掷一枚质地均匀的骰子次,向上一面的点数为的次数大约是( )
A. B. C. D.
下列说法正确的是( )
A. 一组数据,,,,这组数据的中位数是
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是分,分,分,则小明这三次成绩的平均数是分
D. 某日最高气温是,最低气温是,则该日气温的极差是
为了解新冠肺炎疫情防控期间,学生居家进行“线上学习”情况,某班进行了某学科单元基础知识“线上测试”,其中抽查的名学生的成绩如图所示,对于这名学生的测试成绩,下列说法正确( )
A. 中位数是分 B. 众数是分 C. 平均数是分 D. 方差是
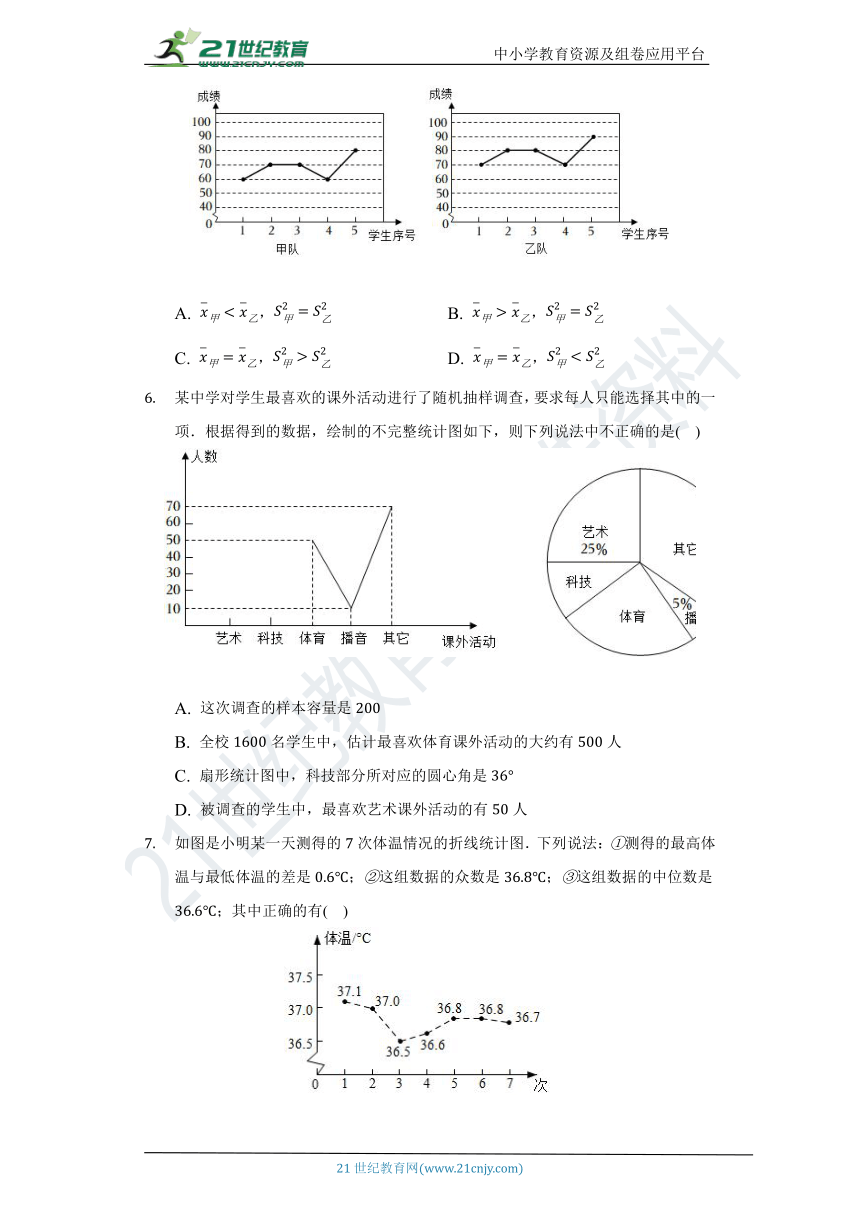
某校在评选“交通安全在我心”优秀宣传小队的活动中,分别对甲、乙两队的名学生进行了交通安全知识考核,其中甲、乙两队学生的考核成绩如图所示,下列关系完全正确的是( )
A. , B. ,
C. , D. ,
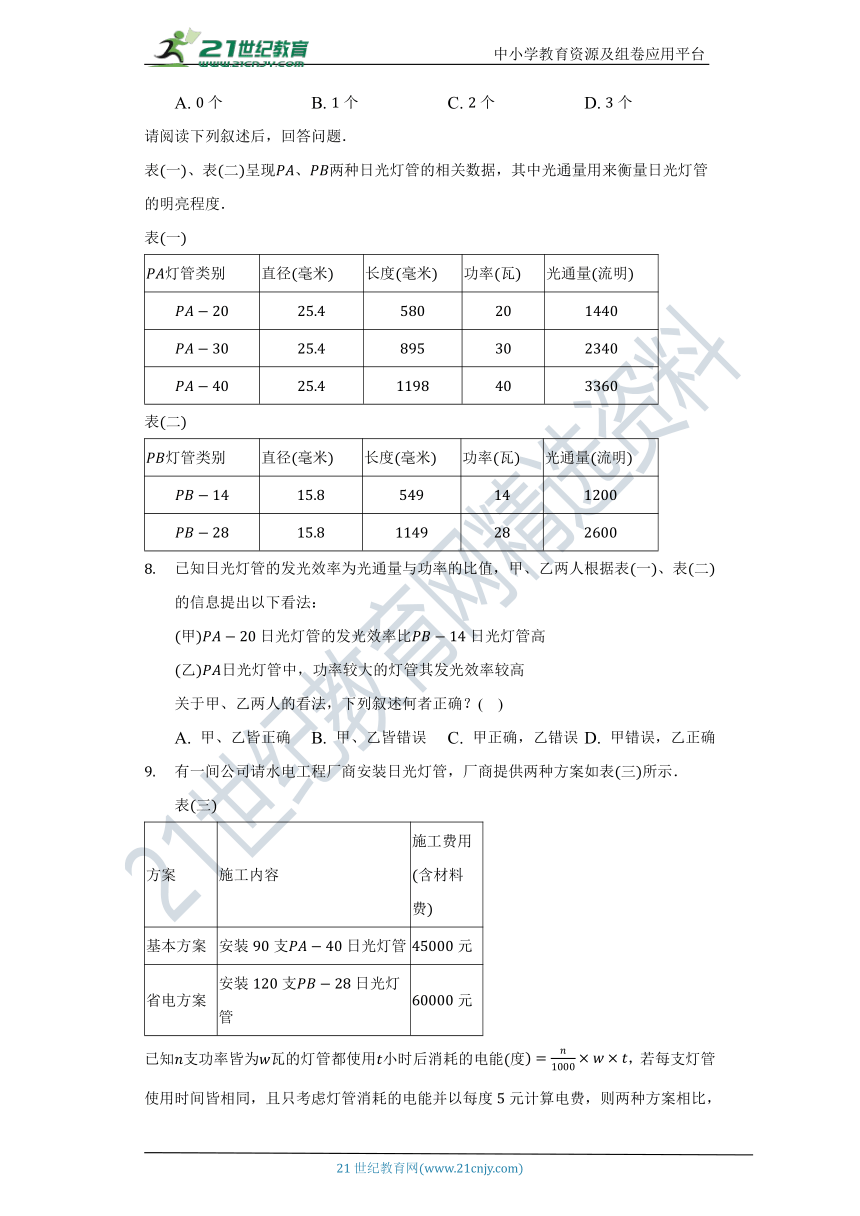
某中学对学生最喜欢的课外活动进行了随机抽样调查,要求每人只能选择其中的一项.根据得到的数据,绘制的不完整统计图如下,则下列说法中不正确的是( )
A. 这次调查的样本容量是
B. 全校名学生中,估计最喜欢体育课外活动的大约有人
C. 扇形统计图中,科技部分所对应的圆心角是
D. 被调查的学生中,最喜欢艺术课外活动的有人
如图是小明某一天测得的次体温情况的折线统计图.下列说法:测得的最高体温与最低体温的差是;这组数据的众数是;这组数据的中位数是;其中正确的有( )
A. 个 B. 个 C. 个 D. 个
请阅读下列叙述后,回答问题.
表一、表二呈现、两种日光灯管的相关数据,其中光通量用来衡量日光灯管的明亮程度.
表一
灯管类别 直径毫米 长度毫米 功率瓦 光通量流明
表二
灯管类别 直径毫米 长度毫米 功率瓦 光通量流明
已知日光灯管的发光效率为光通量与功率的比值,甲、乙两人根据表一、表二的信息提出以下看法:
甲日光灯管的发光效率比日光灯管高
乙日光灯管中,功率较大的灯管其发光效率较高
关于甲、乙两人的看法,下列叙述何者正确?( )
A. 甲、乙皆正确 B. 甲、乙皆错误 C. 甲正确,乙错误 D. 甲错误,乙正确
有一间公司请水电工程厂商安装日光灯管,厂商提供两种方案如表三所示.
表三
方案 施工内容 施工费用含材料费
基本方案 安装支日光灯管 元
省电方案 安装支日光灯管 元
已知支功率皆为瓦的灯管都使用小时后消耗的电能度,若每支灯管使用时间皆相同,且只考虑灯管消耗的电能并以每度元计算电费,则两种方案相比,灯管使用时间至少要超过多少小时,采用省电方案所节省的电费才会高于两者相差的施工费用?( )
A. B. C. D.
从,两个品种的西瓜中随机各取个,它们的质量分布折线图如图.下列统计量中,最能反映出这两组数据之间差异的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
下列说法正确的是( )
A. 打开电视机,它正在播广告是必然事件
B. “明天降水概率“,是指明天有的时间在下雨
C. 方差越大数据的波动越大,方差越小数据的波动越小
D. 在抽样调查过程中,样本容量越小,对总体的估计就越准确
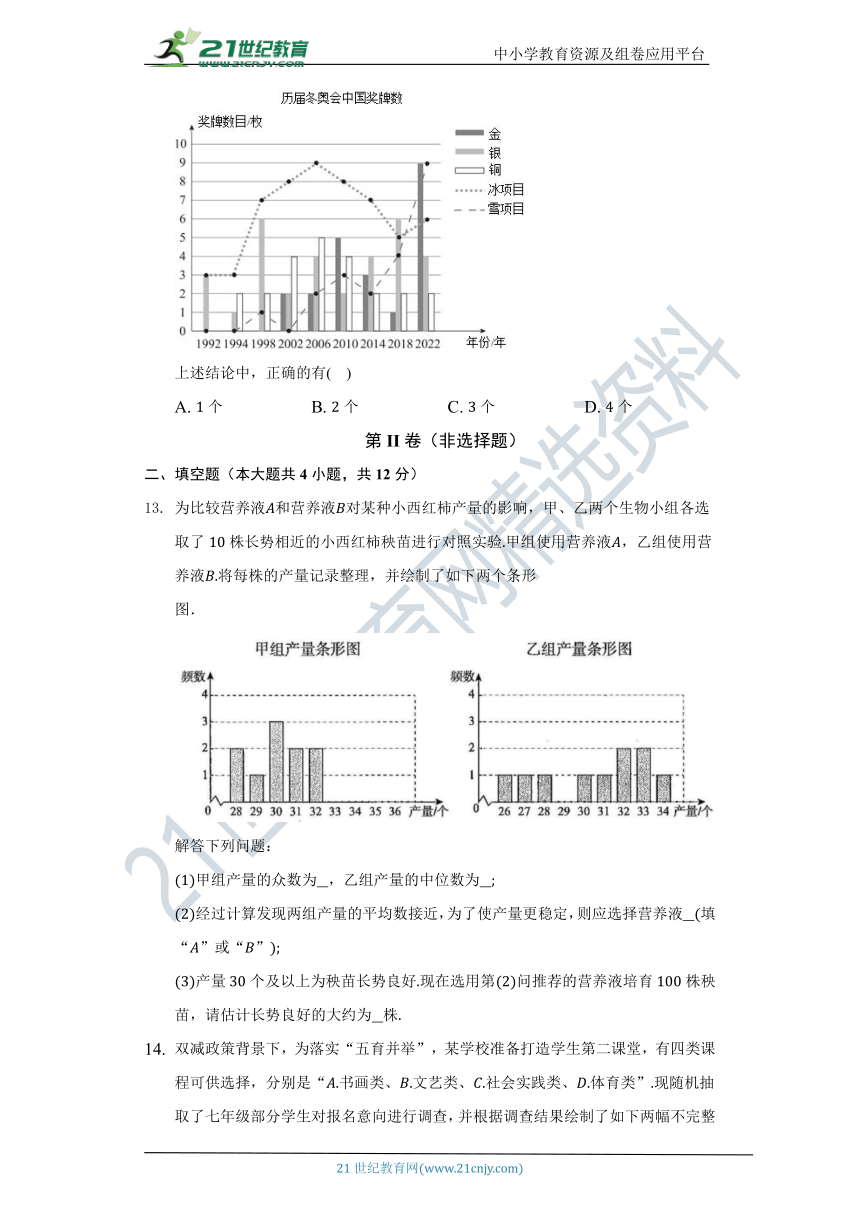
从年初次征战冬奥会,到年取得首枚冬奥会奖牌,再到年北京冬奥会金牌榜前三,中国的冰雪体育事业不断取得突破性成绩.历届冬奥会的比赛项目常被分成两大类:冰项目和雪项目.根据统计图提供的信息,有如下四个结论:
中国队在年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次;
中国队在年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次;
中国队在冬奥会上的冰上项目奖牌数逐年提高;
中国队在冬奥会上的雪上项目奖牌数在年首次超越冰上项目奖牌数.
上述结论中,正确的有( )
A. 个 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
为比较营养液和营养液对某种小西红柿产量的影响,甲、乙两个生物小组各选取了株长势相近的小西红柿秧苗进行对照实验甲组使用营养液,乙组使用营养液将每株的产量记录整理,并绘制了如下两个条形图.
解答下列问题:
甲组产量的众数为 ,乙组产量的中位数为
经过计算发现两组产量的平均数接近,为了使产量更稳定,则应选择营养液 填“”或“”
产量个及以上为秧苗长势良好现在选用第问推荐的营养液培育株秧苗,请估计长势良好的大约为 株
双减政策背景下,为落实“五育并举”,某学校准备打造学生第二课堂,有四类课程可供选择,分别是“书画类、文艺类、社会实践类、体育类”现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了如下两幅不完整的统计图,若该校七年级共有名学生,根据上述调查结果估计该校学生选择“社会实践类”的学生共有______名.
为了估计池塘里有多少条鱼,从池塘里捕捞了条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后再捕捞条,若其中有标记的鱼有条,则估计池塘里共有鱼______条.
为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出条鱼苗,每条做好记号,然后放回原鱼池.一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出条鱼苗,发现其中有记号的鱼苗分别是条、条,可以初步估计鱼苗数目较多的是______鱼池.填甲或乙
三、解答题(本大题共6小题,共48.0分)
疫情期间福州一中初中部举行了“宅家运动会”该学校七、八年级各有名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级:
八年级:
整理数据如下表:
年级
人数
成绩
七年级
八年级
分析数据如下表:
年级 平均数 中位数 众数 方差
七年级
八年级
根据以上信息,回答下列问题:
______,______;
你认为哪个年级“宅家运动会”的总体成绩较好,说明理由至少从两个不同的角度说明推断的合理性;
学校对“宅家运动会”成绩不低于分的学生颁发优胜奖,请你估计学校七八年级所有学生中获得优胜奖的大约有______人.
某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“合格”,“不合格”.
本次抽查总人数为______,“合格”人数的百分比为______;
补全条形统计图;
扇形统计图中“不合格人数”的度数为______;
在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为______.
某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了个活动小组每位学生只能参加一个活动小组:音乐;体育;美术;阅读;人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
此次调查一共随机抽取了______名学生;
补全条形统计图要求在条形图上方注明人数;
扇形统计图中圆心角______度;
若该校有名学生,估计该校参加组阅读的学生人数;
刘老师计划从组人工智能的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.
自年月以来.新型冠状病毒导致的肺炎疫情在全球蔓延流行,进入年,新一轮的疫情爆发又波及校园,严重危及师生的身心健康,为此某校师生举行了“疫情防控大演练”活动,并学习了当前疫情防控的主要措施,包括:远离感染源区;加强自我防控;增强身体体质;合理健康饮食;加强防控意识五个要点,为了了解学生对“五要点”的掌握情况,从全校随机抽取了一部分学生作出调查,并根据学生的回答情况、仅能答出一点;、仅能答出两点;、能回答其中三点;、能回答其中四点;、能回答全部五点,绘制出下面两幅不完整的统计图,请根据统计图上的信息解答下列问题:
在这次调查中抽取的总人数为______人.
在扇形统计图中“”部分值为______.
该学校共有学生人,估计能回答全部五个要点的人数约有多少人?
针对本次学习,学校准备组织一次疫情防控知识竞赛,要求每个班级选取两名同学参赛,小明和小颖所在的九年级某班共选出名候选人,除小明和小颖之外还有另外名同学,从这四人中随机选取两个人参加比赛,请用树状图或列表法求出恰好选中小明和小颖两人的概率这名学生分别用,,,表示,其中,分别代表小明和小颖.
羊城书香浓郁,某校为进一步提升学生阅读水平,组织学生参加阅读大赛.从中抽取部分学生阅读大赛的成绩得分取正整数,满分为分进行统计分析,请根据下列尚未完成的统计图表,解答问题.
组别 分数段 频数 频率
一
二
三
四
五
本次抽样调查的样本容量为______,表中______,并补全频数分布直方图;
若把各组的分数段所占的百分比绘制成扇形统计图,则第三组对应的扇形圆心角的度数是______;
该校一共组织名学生参加阅读大赛,若抽取的样本具有较好的代表性,且成绩超过分为优秀,请估计该校学生中阅读能力优秀的约有多少人?
某校开展“科技知识竞赛”,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.
组别 分数 人数
组
组
组
组
组
合计
根据统计图表提供的信息,解答下列问题:
本次共调查了______名学生;组所在扇形的圆心角为______度;
该校共有学生人,若分以上为优秀,估计该校优秀学生人数为多少?
若组名学生中有人满分,设这名学生为,,,,从其中抽取名学生代表学校参加区级比赛,请用列表或画树状图的方法求恰好抽到,的概率.
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】
【分析】
本题考查统计与概率的可能性大小,概率公式.
先根据一颗质地均匀的骰子的特点求出掷一次向上,每面向上的可能性相同,共有种可能性,点数为的概率为,再求出掷次向上一面的点数为点的次数只要用乘以即可.
【解答】
解:掷一颗骰子有种情况,为其中一种,因此掷一次向上点数为的可能为,
次.
故选D.
3.【答案】
【解析】解:、一组数据,,,,这组数据的中位数是,故此选项错误;
B、了解一批灯泡的使用寿命的情况,适合抽样调查,正确;
C、小明的三次数学成绩是分,分,分,则小明这三次成绩的平均数是分,故此选项错误;
D、某日最高气温是,最低气温是,该日气温的极差是,故此选项错误;
故选:.
直接利用中位数的定义以及抽样调查的意义和平均数的求法、极差的定义分别分析得出答案.
此题主要考查了中位数、抽样调查的意义和平均数的求法、极差,正确把握相关定义是解题关键.
4.【答案】
【解析】
【分析】
本题考查了众数、平均数、中位数以及方差的知识,熟练掌握概念及公式是解题的关键.
A、根据中位数的定义将这组数据从小到大重新排列,求出最中间的个数的平均数,即可得出中位数;
B、根据众数的定义找出出现次数最多的数.
C、根据加权平均数公式代入计算可得;
D、根据方差公式计算即可.
【解答】
解:、中位数是分,错误;
B、众数是分,正确;
C、平均数,错误;
D、方差,错误;
故选:.
5.【答案】
【解析】解:由题意可知,,,
,
由折线统计图可得,
故选:.
根据算术平均数和方差的定义解答即可.
本题考查了平均数和方差,掌握相关定义是解答本题的关键.
6.【答案】
【解析】解:,
这次调查的样本容量为,
故A选项结论正确,不符合题意;
人,
全校名学生中,估计最喜欢体育课外活动的大约有人,
故B选项结论不正确,符合题意;
人,
被调查的学生中,最喜欢艺术课外活动的有人,
故D选项结论正确,不符合题意;
,
扇形统计图中,科技部分所对应的圆心角是,
故C选项结论正确,不符合题意;
故选:.
根据统计图分别判断各个选项即可.
本题主要考查统计的知识,熟练掌握扇形统计图等统计的知识是解题的关键.
7.【答案】
【解析】解:,所以正确.
根据众数定义可知众数为,所以正确.
根据中位数定义可知,中位数应该为,而不是.
故选:.
根据折线图给出的数据,最大值与最小值的差.
根据数据中,众数与中位数的定义来判断即可.
本题主要考查折线统计图、众数、中位数的定义,正确读懂折线统计图,正确理解众数、中位数定义是解题关键.
8~9.【答案】D 、D
【解析】
【分析】
根据“日光灯管的发光效率为光通量与功率的比值”表示出各日光灯管的发光效率然后进行比较即可.
本题考查了统计表,表示出各日光灯管的发光效率是解题的关键.
【解答】
解:根据题意,日光灯管的发光效率为,
日光灯管的发光效率为,
,
日光灯管发光效率高,
故甲错误;
日光灯管的发光效率为,
日光灯管的发光效率为,
日光灯管的发光效率为,
时,,
日光灯管中,功率较大的灯管其发光效率较高,
故乙正确,
故选:.
【分析】
根据“采用省电方案所节省的电费才会高于两者相差的施工费用”列一元一次不等式,求解即可.
本题考查了一元一次不等式的应用,理解题意并根据题意建立一元一次不等式是解题的关键.
【解答】
解:根据题意,得,
解得,
灯管使用时间超过小时,采用省电方案所节省的电费才会高于两者相差的施工费用,
故选:.
10.【答案】
【解析】解:由图可得,
,
,
故反映出这两组数据之间差异不能反映出这两组数据之间差异,故选项A不符合题意;
和的中位数和众数都相等,故不能反映出这两组数据之间差异,故选项B和不符合题意;
由图象可得,种数据波动小,比较稳定,种数据波动大,不稳定,能反映出这两组数据之间差异,故选项D符合题意;
故选:.
根据统计图中的数据,可以判断哪个选项符合题意,本题得以解决.
本题考查折线统计图、中位数、众数、平均数、方差,解答本题的关键是明确题意,利用数形结合的思想解答.
11.【答案】
【解析】解:、打开电视机,它正在播广告是随机事件,故本选项错误;
B、“明天降水概率“,意味着明天降雨的可能是,故本选项错误;
C、方差越大数据的波动越大,方差越小数据的波动越小,故本选项正确;
D、在抽样调查过程中,样本容量越大,对总体的估计就越准确,故本选项错误;
故选:.
根据必然事件的概念、方差的定义、随机事件的概率逐项分析即可得出答案.
本题考查了必然事件的概念、方差的定义、求随机事件的概率,解题的关键是熟练掌握方差的定义以及求随机事件的概率.
12.【答案】
【解析】解:由题意可知,中国队在年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次,故说法正确;
中国队在年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次,故说法正确;
中国队在冬奥会上的冰上项目奖牌数在年和年持平,年奖牌数为枚,年也是枚,故说法错误;
中国队在冬奥会上的雪上项目奖牌数在年首次超越冰上项目奖牌数,故说法正确;
所以正确的有个.
故选:.
根据统计图逐一判断即可.
本题考查折线统计图和条形统计图,利用数形结合的方法是解决问题的关键.
13.【答案】,
【解析】
【分析】
此题主要考查众数及中位数的定义及方差,用样本估计总体
利用众数及中位数的定义求解
先计算平均数与方差,进行比较求解
用样本估计总体:先求出涨势良好的株数,根据良好株数的占比求解
【解答】
解:观察条形图,出现频数最多的数据就是众数,则甲组产量的众数为
将乙组产量按照频数从小到大排序得:,,,,,,,。
一共有个数据,则中位数就是第个和第个数据的平均数,
即乙组产量的中位数为
计算两组产量的平均数,
甲组
乙组
要使得产量更稳定,则要求产量的方差要小,
所以
所以甲组产量更加稳定,因此应选择营养液
观察甲组条形图,
产量个及以上的秧苗有株,
占比,
因此估计长势良好的大约为株.
14.【答案】
【解析】
【分析】
本题主要考查的是扇形统计图,条形统计图,用样本估计总体的有关知识,先求出学生选择“社会实践类”对应的百分比,然后乘以进行计算即可.
【解答】
解:由题意得
人,
该校学生选择“社会实践类”的学生共有:
名.
15.【答案】
【解析】解:则估计池塘里共有鱼条,
故答案为:.
用原做标记的鱼的数量除以所抽取样本中做标记的鱼的数量所占比例即可.
本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
16.【答案】甲
【解析】解:由题意可得,
甲鱼池中的鱼苗数量约为:条,
乙鱼池中的鱼苗数量约为:条,
,
初步估计鱼苗数目较多的是甲鱼池,
故答案为:甲.
根据题意和题目中的数据可以计算出甲鱼池和乙鱼池中鱼苗的数量,然后比较大小即可.
本题考查用样本估计总体,解答本题的关键是求出两个鱼池中鱼苗的数量.
17.【答案】 ,
【解析】解:,
;
八年级成绩较好,八年级成绩的众数、中位数比七年级成绩相应的众数、中位数都要大,说明八年级成绩的集中趋势要高,方差八年级较小,说明八年级的成绩比较稳定.
七年级优秀人数为:人,
八年级优秀人数为:人.
故学校七八年级所有学生中获得优胜奖的大约有,人.
故答案为:,;,.
从调查的七年级的人数减去前几组的人数即可,将八年级的名学生的成绩排序后找到第、个数的平均数即是八年级的中位数;
从中位数、众数、方差进行分析,调查结论,
用各个年级的总人数乘样本中优秀人数所占的比即可.
本题考查了众数、中位数以及平均数,掌握众数、中位数以及平均数的定义是解题的关键.
18.【答案】人
【解析】解:本次抽查的总人数为人,
“合格”人数的百分比为,
故答案为:人,;
补全图形如下:
扇形统计图中“不合格人数”的度数为,
故答案为:;
列表如下:
甲 乙 丙
甲 乙,甲 丙,甲
乙 甲,乙 丙,乙
丙 甲,丙 乙,丙
由表知,共有种等可能结果,其中刚好抽中甲乙两人的有种结果,
所以刚好抽中甲乙两人的概率为.
故答案为:.
由优秀人数及其所占百分比可得总人数,根据百分比之和为可得合格人数所占百分比;
总人数乘以不合格人数所占百分比求出其人数,从而补全图形;
用乘以样本中“不合格人数”所占百分比即可得出答案;
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
此题考查了列表法与树状图法,用到的知识点为:概率所求情况数与总情况数之比.
19.【答案】
【解析】解:此次调查一共随机抽取的学生人数为:名,
故答案为:;
组的人数为:名,
补全条形统计图如下:
扇形统计图中圆心角,
故答案为:;
名,
答:估计该校参加组阅读的学生人数为名;
画树状图如下:
共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,
恰好抽中甲、乙两人的概率为.
由组的人数除以所占百分比即可;
求出组的人数,补全条形统计图即可;
由乘以组所占的比例即可;
由该校共有学生人数乘以参加组阅读的学生人数所占的比例即可;
画树状图,共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率以及条形统计图和扇形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
20.【答案】
【解析】解:本次调查的总人数为人,
故答案为:;
,即;
故答案为:.
估计能回答全部五个要点的人数约有人;
画树状图得:
一共有种可能出现的结果,它们都是等可能的,符合条件的有种,
恰好选中小明和小颖两人的概率为.
由类别人数及其所占百分比可得总人数;
用类别人数除以总人数可得的值,继而得出答案;
用总人数乘以样本中类别人数所占比例即可;
画出树状图,共有个等可能的结果,其中小明和小颖参加同一项目的结果有个,再由概率公式求解即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.同时考查了概率公式.
21.【答案】
【解析】解:样本容量为,
则,
补全直方图如下:
;
第三组对应的扇形圆心角的度数是,
故答案为:;
人.
答:估计该校学生中阅读能力优秀的约有人.
由第一组的人数及其所占百分比可得样本容量,样本容量乘以第四组对应的频率即可求出的值,据此即可补全图形;
用乘以第三组对应频率即可;
用总人数乘以样本中第四、五组的频率和即可.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
22.【答案】
【解析】解:调查人数为:人,
,
故答案为:,;
“组”的人数为:人,
“组”的人数为:人,
因此成绩为优秀分以上共有人,
人,
答:该校名学生中,成绩为优秀的大约有人;
从,,,这四名学生中抽取名,所有可能出现的结果如下:
共有种可能出现的结果,其中抽到,的有种,
所以抽到,的概率为.
从两个统计图表中可知,“组”的频数为,占调查人数的,根据频率进行计算即可;进而求出相应圆心角的度数;
先求出“组”人数,再求出“组”人数,根据分及以上学生所占的百分比进行计算即可;
用列表法表示从,,,这四名学生中抽取名,所有可能出现的结果,再根据概率的定义进行计算即可.
本题考查频数分布表、扇形统计图以及列表法求简单随机事件的概率,掌握频率以及列举出所有可能出现的结果是正确解答的前提.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
8.6收取多少保险费才合理苏科版初中数学九年级下册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
某地旅游管理部门在某景区随机调查了名游客,其中有名游客对该景区的服务表示满意对于此次调查,下列说法正确的是( )
A. 若随机调查名游客,则该游客表示满意的概率约为
B. 若随机调查名游客,则一定有名游客表示满意
C. 在所有到该景区旅游的游客中,只有名游客表示满意
D. 本次调查采用的方式是普查
抛掷一枚质地均匀的骰子次,向上一面的点数为的次数大约是( )
A. B. C. D.
下列说法正确的是( )
A. 一组数据,,,,这组数据的中位数是
B. 了解一批灯泡的使用寿命的情况,适合抽样调查
C. 小明的三次数学成绩是分,分,分,则小明这三次成绩的平均数是分
D. 某日最高气温是,最低气温是,则该日气温的极差是
为了解新冠肺炎疫情防控期间,学生居家进行“线上学习”情况,某班进行了某学科单元基础知识“线上测试”,其中抽查的名学生的成绩如图所示,对于这名学生的测试成绩,下列说法正确( )
A. 中位数是分 B. 众数是分 C. 平均数是分 D. 方差是
某校在评选“交通安全在我心”优秀宣传小队的活动中,分别对甲、乙两队的名学生进行了交通安全知识考核,其中甲、乙两队学生的考核成绩如图所示,下列关系完全正确的是( )
A. , B. ,
C. , D. ,
某中学对学生最喜欢的课外活动进行了随机抽样调查,要求每人只能选择其中的一项.根据得到的数据,绘制的不完整统计图如下,则下列说法中不正确的是( )
A. 这次调查的样本容量是
B. 全校名学生中,估计最喜欢体育课外活动的大约有人
C. 扇形统计图中,科技部分所对应的圆心角是
D. 被调查的学生中,最喜欢艺术课外活动的有人
如图是小明某一天测得的次体温情况的折线统计图.下列说法:测得的最高体温与最低体温的差是;这组数据的众数是;这组数据的中位数是;其中正确的有( )
A. 个 B. 个 C. 个 D. 个
请阅读下列叙述后,回答问题.
表一、表二呈现、两种日光灯管的相关数据,其中光通量用来衡量日光灯管的明亮程度.
表一
灯管类别 直径毫米 长度毫米 功率瓦 光通量流明
表二
灯管类别 直径毫米 长度毫米 功率瓦 光通量流明
已知日光灯管的发光效率为光通量与功率的比值,甲、乙两人根据表一、表二的信息提出以下看法:
甲日光灯管的发光效率比日光灯管高
乙日光灯管中,功率较大的灯管其发光效率较高
关于甲、乙两人的看法,下列叙述何者正确?( )
A. 甲、乙皆正确 B. 甲、乙皆错误 C. 甲正确,乙错误 D. 甲错误,乙正确
有一间公司请水电工程厂商安装日光灯管,厂商提供两种方案如表三所示.
表三
方案 施工内容 施工费用含材料费
基本方案 安装支日光灯管 元
省电方案 安装支日光灯管 元
已知支功率皆为瓦的灯管都使用小时后消耗的电能度,若每支灯管使用时间皆相同,且只考虑灯管消耗的电能并以每度元计算电费,则两种方案相比,灯管使用时间至少要超过多少小时,采用省电方案所节省的电费才会高于两者相差的施工费用?( )
A. B. C. D.
从,两个品种的西瓜中随机各取个,它们的质量分布折线图如图.下列统计量中,最能反映出这两组数据之间差异的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
下列说法正确的是( )
A. 打开电视机,它正在播广告是必然事件
B. “明天降水概率“,是指明天有的时间在下雨
C. 方差越大数据的波动越大,方差越小数据的波动越小
D. 在抽样调查过程中,样本容量越小,对总体的估计就越准确
从年初次征战冬奥会,到年取得首枚冬奥会奖牌,再到年北京冬奥会金牌榜前三,中国的冰雪体育事业不断取得突破性成绩.历届冬奥会的比赛项目常被分成两大类:冰项目和雪项目.根据统计图提供的信息,有如下四个结论:
中国队在年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次;
中国队在年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次;
中国队在冬奥会上的冰上项目奖牌数逐年提高;
中国队在冬奥会上的雪上项目奖牌数在年首次超越冰上项目奖牌数.
上述结论中,正确的有( )
A. 个 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
为比较营养液和营养液对某种小西红柿产量的影响,甲、乙两个生物小组各选取了株长势相近的小西红柿秧苗进行对照实验甲组使用营养液,乙组使用营养液将每株的产量记录整理,并绘制了如下两个条形图.
解答下列问题:
甲组产量的众数为 ,乙组产量的中位数为
经过计算发现两组产量的平均数接近,为了使产量更稳定,则应选择营养液 填“”或“”
产量个及以上为秧苗长势良好现在选用第问推荐的营养液培育株秧苗,请估计长势良好的大约为 株
双减政策背景下,为落实“五育并举”,某学校准备打造学生第二课堂,有四类课程可供选择,分别是“书画类、文艺类、社会实践类、体育类”现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了如下两幅不完整的统计图,若该校七年级共有名学生,根据上述调查结果估计该校学生选择“社会实践类”的学生共有______名.
为了估计池塘里有多少条鱼,从池塘里捕捞了条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后再捕捞条,若其中有标记的鱼有条,则估计池塘里共有鱼______条.
为了比较甲、乙两鱼池中的鱼苗数目,小明从两鱼池中各捞出条鱼苗,每条做好记号,然后放回原鱼池.一段时间后,在同样的地方,小明再从甲、乙两鱼池中各捞出条鱼苗,发现其中有记号的鱼苗分别是条、条,可以初步估计鱼苗数目较多的是______鱼池.填甲或乙
三、解答题(本大题共6小题,共48.0分)
疫情期间福州一中初中部举行了“宅家运动会”该学校七、八年级各有名学生参加了这次“宅家运动会”,现从七、八年级各随机抽取名学生宅家运动会的成绩进行抽样调查.
收集数据如下:
七年级:
八年级:
整理数据如下表:
年级
人数
成绩
七年级
八年级
分析数据如下表:
年级 平均数 中位数 众数 方差
七年级
八年级
根据以上信息,回答下列问题:
______,______;
你认为哪个年级“宅家运动会”的总体成绩较好,说明理由至少从两个不同的角度说明推断的合理性;
学校对“宅家运动会”成绩不低于分的学生颁发优胜奖,请你估计学校七八年级所有学生中获得优胜奖的大约有______人.
某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有“优秀”,“合格”,“不合格”.
本次抽查总人数为______,“合格”人数的百分比为______;
补全条形统计图;
扇形统计图中“不合格人数”的度数为______;
在“优秀”中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为______.
某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了个活动小组每位学生只能参加一个活动小组:音乐;体育;美术;阅读;人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
此次调查一共随机抽取了______名学生;
补全条形统计图要求在条形图上方注明人数;
扇形统计图中圆心角______度;
若该校有名学生,估计该校参加组阅读的学生人数;
刘老师计划从组人工智能的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.
自年月以来.新型冠状病毒导致的肺炎疫情在全球蔓延流行,进入年,新一轮的疫情爆发又波及校园,严重危及师生的身心健康,为此某校师生举行了“疫情防控大演练”活动,并学习了当前疫情防控的主要措施,包括:远离感染源区;加强自我防控;增强身体体质;合理健康饮食;加强防控意识五个要点,为了了解学生对“五要点”的掌握情况,从全校随机抽取了一部分学生作出调查,并根据学生的回答情况、仅能答出一点;、仅能答出两点;、能回答其中三点;、能回答其中四点;、能回答全部五点,绘制出下面两幅不完整的统计图,请根据统计图上的信息解答下列问题:
在这次调查中抽取的总人数为______人.
在扇形统计图中“”部分值为______.
该学校共有学生人,估计能回答全部五个要点的人数约有多少人?
针对本次学习,学校准备组织一次疫情防控知识竞赛,要求每个班级选取两名同学参赛,小明和小颖所在的九年级某班共选出名候选人,除小明和小颖之外还有另外名同学,从这四人中随机选取两个人参加比赛,请用树状图或列表法求出恰好选中小明和小颖两人的概率这名学生分别用,,,表示,其中,分别代表小明和小颖.
羊城书香浓郁,某校为进一步提升学生阅读水平,组织学生参加阅读大赛.从中抽取部分学生阅读大赛的成绩得分取正整数,满分为分进行统计分析,请根据下列尚未完成的统计图表,解答问题.
组别 分数段 频数 频率
一
二
三
四
五
本次抽样调查的样本容量为______,表中______,并补全频数分布直方图;
若把各组的分数段所占的百分比绘制成扇形统计图,则第三组对应的扇形圆心角的度数是______;
该校一共组织名学生参加阅读大赛,若抽取的样本具有较好的代表性,且成绩超过分为优秀,请估计该校学生中阅读能力优秀的约有多少人?
某校开展“科技知识竞赛”,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.
组别 分数 人数
组
组
组
组
组
合计
根据统计图表提供的信息,解答下列问题:
本次共调查了______名学生;组所在扇形的圆心角为______度;
该校共有学生人,若分以上为优秀,估计该校优秀学生人数为多少?
若组名学生中有人满分,设这名学生为,,,,从其中抽取名学生代表学校参加区级比赛,请用列表或画树状图的方法求恰好抽到,的概率.
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】
【分析】
本题考查统计与概率的可能性大小,概率公式.
先根据一颗质地均匀的骰子的特点求出掷一次向上,每面向上的可能性相同,共有种可能性,点数为的概率为,再求出掷次向上一面的点数为点的次数只要用乘以即可.
【解答】
解:掷一颗骰子有种情况,为其中一种,因此掷一次向上点数为的可能为,
次.
故选D.
3.【答案】
【解析】解:、一组数据,,,,这组数据的中位数是,故此选项错误;
B、了解一批灯泡的使用寿命的情况,适合抽样调查,正确;
C、小明的三次数学成绩是分,分,分,则小明这三次成绩的平均数是分,故此选项错误;
D、某日最高气温是,最低气温是,该日气温的极差是,故此选项错误;
故选:.
直接利用中位数的定义以及抽样调查的意义和平均数的求法、极差的定义分别分析得出答案.
此题主要考查了中位数、抽样调查的意义和平均数的求法、极差,正确把握相关定义是解题关键.
4.【答案】
【解析】
【分析】
本题考查了众数、平均数、中位数以及方差的知识,熟练掌握概念及公式是解题的关键.
A、根据中位数的定义将这组数据从小到大重新排列,求出最中间的个数的平均数,即可得出中位数;
B、根据众数的定义找出出现次数最多的数.
C、根据加权平均数公式代入计算可得;
D、根据方差公式计算即可.
【解答】
解:、中位数是分,错误;
B、众数是分,正确;
C、平均数,错误;
D、方差,错误;
故选:.
5.【答案】
【解析】解:由题意可知,,,
,
由折线统计图可得,
故选:.
根据算术平均数和方差的定义解答即可.
本题考查了平均数和方差,掌握相关定义是解答本题的关键.
6.【答案】
【解析】解:,
这次调查的样本容量为,
故A选项结论正确,不符合题意;
人,
全校名学生中,估计最喜欢体育课外活动的大约有人,
故B选项结论不正确,符合题意;
人,
被调查的学生中,最喜欢艺术课外活动的有人,
故D选项结论正确,不符合题意;
,
扇形统计图中,科技部分所对应的圆心角是,
故C选项结论正确,不符合题意;
故选:.
根据统计图分别判断各个选项即可.
本题主要考查统计的知识,熟练掌握扇形统计图等统计的知识是解题的关键.
7.【答案】
【解析】解:,所以正确.
根据众数定义可知众数为,所以正确.
根据中位数定义可知,中位数应该为,而不是.
故选:.
根据折线图给出的数据,最大值与最小值的差.
根据数据中,众数与中位数的定义来判断即可.
本题主要考查折线统计图、众数、中位数的定义,正确读懂折线统计图,正确理解众数、中位数定义是解题关键.
8~9.【答案】D 、D
【解析】
【分析】
根据“日光灯管的发光效率为光通量与功率的比值”表示出各日光灯管的发光效率然后进行比较即可.
本题考查了统计表,表示出各日光灯管的发光效率是解题的关键.
【解答】
解:根据题意,日光灯管的发光效率为,
日光灯管的发光效率为,
,
日光灯管发光效率高,
故甲错误;
日光灯管的发光效率为,
日光灯管的发光效率为,
日光灯管的发光效率为,
时,,
日光灯管中,功率较大的灯管其发光效率较高,
故乙正确,
故选:.
【分析】
根据“采用省电方案所节省的电费才会高于两者相差的施工费用”列一元一次不等式,求解即可.
本题考查了一元一次不等式的应用,理解题意并根据题意建立一元一次不等式是解题的关键.
【解答】
解:根据题意,得,
解得,
灯管使用时间超过小时,采用省电方案所节省的电费才会高于两者相差的施工费用,
故选:.
10.【答案】
【解析】解:由图可得,
,
,
故反映出这两组数据之间差异不能反映出这两组数据之间差异,故选项A不符合题意;
和的中位数和众数都相等,故不能反映出这两组数据之间差异,故选项B和不符合题意;
由图象可得,种数据波动小,比较稳定,种数据波动大,不稳定,能反映出这两组数据之间差异,故选项D符合题意;
故选:.
根据统计图中的数据,可以判断哪个选项符合题意,本题得以解决.
本题考查折线统计图、中位数、众数、平均数、方差,解答本题的关键是明确题意,利用数形结合的思想解答.
11.【答案】
【解析】解:、打开电视机,它正在播广告是随机事件,故本选项错误;
B、“明天降水概率“,意味着明天降雨的可能是,故本选项错误;
C、方差越大数据的波动越大,方差越小数据的波动越小,故本选项正确;
D、在抽样调查过程中,样本容量越大,对总体的估计就越准确,故本选项错误;
故选:.
根据必然事件的概念、方差的定义、随机事件的概率逐项分析即可得出答案.
本题考查了必然事件的概念、方差的定义、求随机事件的概率,解题的关键是熟练掌握方差的定义以及求随机事件的概率.
12.【答案】
【解析】解:由题意可知,中国队在年北京冬奥会上获得的金牌数是参加冬奥会以来最多的一次,故说法正确;
中国队在年北京冬奥会上获得的奖牌数是参加冬奥会以来最多的一次,故说法正确;
中国队在冬奥会上的冰上项目奖牌数在年和年持平,年奖牌数为枚,年也是枚,故说法错误;
中国队在冬奥会上的雪上项目奖牌数在年首次超越冰上项目奖牌数,故说法正确;
所以正确的有个.
故选:.
根据统计图逐一判断即可.
本题考查折线统计图和条形统计图,利用数形结合的方法是解决问题的关键.
13.【答案】,
【解析】
【分析】
此题主要考查众数及中位数的定义及方差,用样本估计总体
利用众数及中位数的定义求解
先计算平均数与方差,进行比较求解
用样本估计总体:先求出涨势良好的株数,根据良好株数的占比求解
【解答】
解:观察条形图,出现频数最多的数据就是众数,则甲组产量的众数为
将乙组产量按照频数从小到大排序得:,,,,,,,。
一共有个数据,则中位数就是第个和第个数据的平均数,
即乙组产量的中位数为
计算两组产量的平均数,
甲组
乙组
要使得产量更稳定,则要求产量的方差要小,
所以
所以甲组产量更加稳定,因此应选择营养液
观察甲组条形图,
产量个及以上的秧苗有株,
占比,
因此估计长势良好的大约为株.
14.【答案】
【解析】
【分析】
本题主要考查的是扇形统计图,条形统计图,用样本估计总体的有关知识,先求出学生选择“社会实践类”对应的百分比,然后乘以进行计算即可.
【解答】
解:由题意得
人,
该校学生选择“社会实践类”的学生共有:
名.
15.【答案】
【解析】解:则估计池塘里共有鱼条,
故答案为:.
用原做标记的鱼的数量除以所抽取样本中做标记的鱼的数量所占比例即可.
本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
16.【答案】甲
【解析】解:由题意可得,
甲鱼池中的鱼苗数量约为:条,
乙鱼池中的鱼苗数量约为:条,
,
初步估计鱼苗数目较多的是甲鱼池,
故答案为:甲.
根据题意和题目中的数据可以计算出甲鱼池和乙鱼池中鱼苗的数量,然后比较大小即可.
本题考查用样本估计总体,解答本题的关键是求出两个鱼池中鱼苗的数量.
17.【答案】 ,
【解析】解:,
;
八年级成绩较好,八年级成绩的众数、中位数比七年级成绩相应的众数、中位数都要大,说明八年级成绩的集中趋势要高,方差八年级较小,说明八年级的成绩比较稳定.
七年级优秀人数为:人,
八年级优秀人数为:人.
故学校七八年级所有学生中获得优胜奖的大约有,人.
故答案为:,;,.
从调查的七年级的人数减去前几组的人数即可,将八年级的名学生的成绩排序后找到第、个数的平均数即是八年级的中位数;
从中位数、众数、方差进行分析,调查结论,
用各个年级的总人数乘样本中优秀人数所占的比即可.
本题考查了众数、中位数以及平均数,掌握众数、中位数以及平均数的定义是解题的关键.
18.【答案】人
【解析】解:本次抽查的总人数为人,
“合格”人数的百分比为,
故答案为:人,;
补全图形如下:
扇形统计图中“不合格人数”的度数为,
故答案为:;
列表如下:
甲 乙 丙
甲 乙,甲 丙,甲
乙 甲,乙 丙,乙
丙 甲,丙 乙,丙
由表知,共有种等可能结果,其中刚好抽中甲乙两人的有种结果,
所以刚好抽中甲乙两人的概率为.
故答案为:.
由优秀人数及其所占百分比可得总人数,根据百分比之和为可得合格人数所占百分比;
总人数乘以不合格人数所占百分比求出其人数,从而补全图形;
用乘以样本中“不合格人数”所占百分比即可得出答案;
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
此题考查了列表法与树状图法,用到的知识点为:概率所求情况数与总情况数之比.
19.【答案】
【解析】解:此次调查一共随机抽取的学生人数为:名,
故答案为:;
组的人数为:名,
补全条形统计图如下:
扇形统计图中圆心角,
故答案为:;
名,
答:估计该校参加组阅读的学生人数为名;
画树状图如下:
共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,
恰好抽中甲、乙两人的概率为.
由组的人数除以所占百分比即可;
求出组的人数,补全条形统计图即可;
由乘以组所占的比例即可;
由该校共有学生人数乘以参加组阅读的学生人数所占的比例即可;
画树状图,共有种等可能的结果,其中恰好抽中甲、乙两人的结果有种,再由概率公式求解即可.
本题考查的是用树状图法求概率以及条形统计图和扇形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
20.【答案】
【解析】解:本次调查的总人数为人,
故答案为:;
,即;
故答案为:.
估计能回答全部五个要点的人数约有人;
画树状图得:
一共有种可能出现的结果,它们都是等可能的,符合条件的有种,
恰好选中小明和小颖两人的概率为.
由类别人数及其所占百分比可得总人数;
用类别人数除以总人数可得的值,继而得出答案;
用总人数乘以样本中类别人数所占比例即可;
画出树状图,共有个等可能的结果,其中小明和小颖参加同一项目的结果有个,再由概率公式求解即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.同时考查了概率公式.
21.【答案】
【解析】解:样本容量为,
则,
补全直方图如下:
;
第三组对应的扇形圆心角的度数是,
故答案为:;
人.
答:估计该校学生中阅读能力优秀的约有人.
由第一组的人数及其所占百分比可得样本容量,样本容量乘以第四组对应的频率即可求出的值,据此即可补全图形;
用乘以第三组对应频率即可;
用总人数乘以样本中第四、五组的频率和即可.
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
22.【答案】
【解析】解:调查人数为:人,
,
故答案为:,;
“组”的人数为:人,
“组”的人数为:人,
因此成绩为优秀分以上共有人,
人,
答:该校名学生中,成绩为优秀的大约有人;
从,,,这四名学生中抽取名,所有可能出现的结果如下:
共有种可能出现的结果,其中抽到,的有种,
所以抽到,的概率为.
从两个统计图表中可知,“组”的频数为,占调查人数的,根据频率进行计算即可;进而求出相应圆心角的度数;
先求出“组”人数,再求出“组”人数,根据分及以上学生所占的百分比进行计算即可;
用列表法表示从,,,这四名学生中抽取名,所有可能出现的结果,再根据概率的定义进行计算即可.
本题考查频数分布表、扇形统计图以及列表法求简单随机事件的概率,掌握频率以及列举出所有可能出现的结果是正确解答的前提.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
