高一新生入学分班考试数学模拟试卷(PDF版含答案)
文档属性
| 名称 | 高一新生入学分班考试数学模拟试卷(PDF版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 512.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-13 16:10:50 | ||
图片预览

文档简介
高一新生入学分班考试数学模拟试卷( 2)
一、填空题(每题 4 分)
2
1. 已知实数 x, y满足 x + 3x + y 3 = 0,则 x + y 的最大值为__________.
2. 直线 l1 : y = x +1与直线 l2 : y = mx + n相交于点 P(a,2),则m 2 时关于 x 的不等式 x+1 mx+ n
的解为__________.
3. 随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费标准按原标准每分钟降低了 a 元后,再次
下调了 25%,现在的收费标准是每分钟b 元,则原收费标准为__________元(用a,b表示)
2 2 b 1 a 1
4. 若实数 a b,且a,b满足a 8a + 5 = 0,b 8b + 5 = 0 ,则代数式 + 的值为__________.
a 1 b 1
5. 如图,已知直线 l1 / /l2 / /l3 / /l4 ,相邻两条平行直线间的距离都是 1,如果正方
形 ABCD的四个顶点分别在四条直线上,则 sin =__________.
6. 已知a+b+ c = 4,ab+bc+ ac = 5,则a2 +b2 + c2 = __________.
7. 商场的自动扶梯在匀速上升,一男孩与一女孩在这自动扶梯上往上爬,已知
男孩往上爬的速度是女孩往上爬的速度的 2 倍,男孩爬了 27 级到楼上,女孩爬
18 级到楼上,则从楼下到楼上自动扶梯的级数是__________.
8. 相交两圆的公共弦长为 16cm,若两圆的半径长分别为 10cm 和 17cm,则这
两圆的圆心距为__________cm
9. 如图,等边 ABC 的边长为 6, AD是 BC 边上的中线,M 是 AD上的动
点, E 是 AC 边上一点,若 AE = 2, EM +CM 的最小值为__________.
10. 用一长度为 l 的铁丝围成一个封闭图形,则其所围成的图形
的最大面积为__________.
11. 将图甲中阴影部分的小长方形变换到图乙位置,你能根据两
个图形的面积关系得到的数学公式是__________.
12. 在课外活动时间,小王、小丽、小华做“互相踢毽子”游戏,
毽子从一人传到另一人就记为踢一次,若经过三次踢毽后,毽子
踢到小王处的可能性最小,应从__________开始踢
13. 如图,n+1个上底、两腰长皆为 1,下底长为 2 的等腰梯形的下底均在同一直线上,设四边形 P1M1N1N2
面积为 S1 ,四边形 P2M 2N3N3 的面积为 S2 ,……,四边形 PnM nNnNn+1 的面积记为 Sn ,通过逐一计算
S1, S2 , ,可得 Sn = __________.
第 1 页
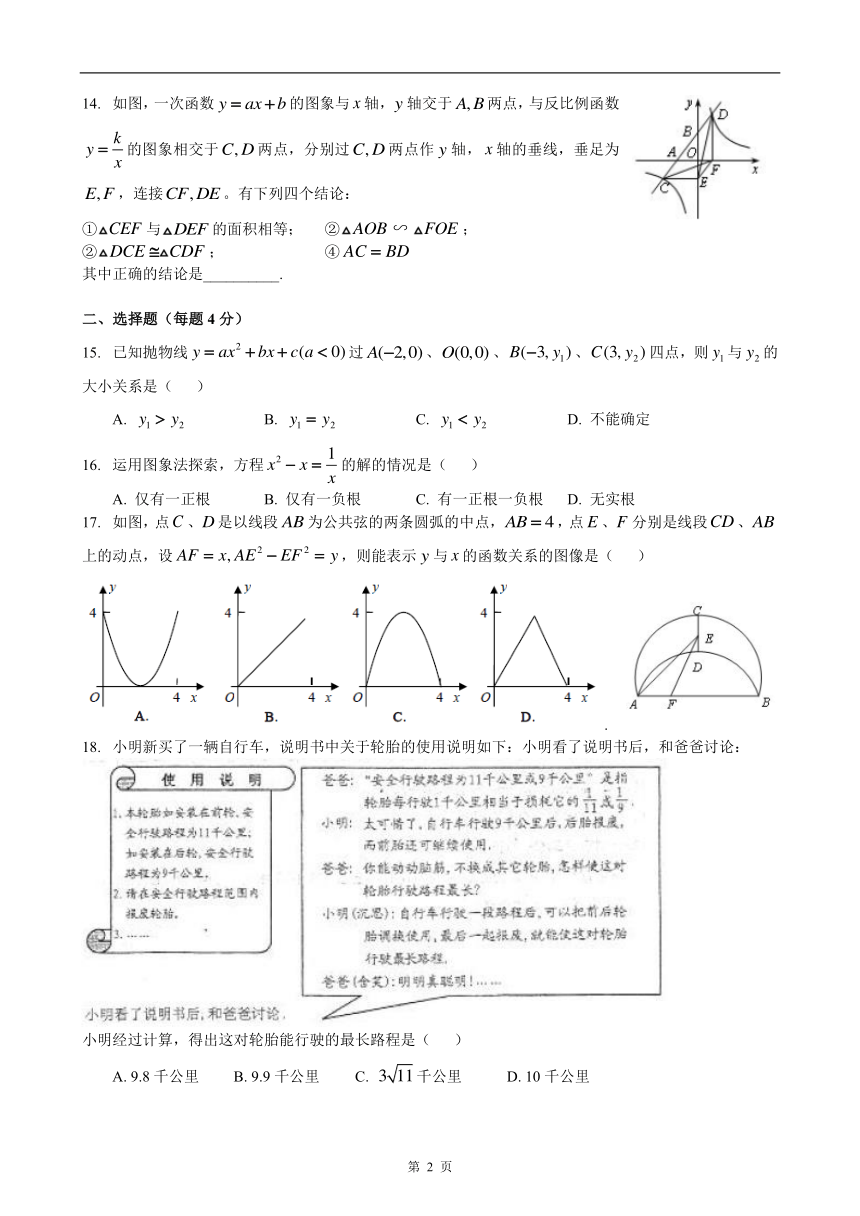
14. 如图,一次函数 y = ax+ b的图象与 x 轴,y 轴交于 A, B两点,与反比例函数
k
y = 的图象相交于C, D 两点,分别过C, D 两点作 y 轴, x 轴的垂线,垂足为
x
E,F ,连接CF,DE。有下列四个结论:
① CEF 与 DEF 的面积相等; ② AOB ∽ FOE ;
② DCE CDF ; ④ AC = BD
其中正确的结论是__________.
二、选择题(每题 4 分)
2
15. 已知抛物线 y = ax + bx + c(a 0)过 A( 2,0)、O(0,0) 、B( 3, y1) 、C(3, y2 ) 四点,则 y1 与 y2 的
大小关系是( )
A. y1 y2 B. y1 = y2 C. y1 y2 D. 不能确定
2 1
16. 运用图象法探索,方程 x x = 的解的情况是( )
x
A. 仅有一正根 B. 仅有一负根 C. 有一正根一负根 D. 无实根
17. 如图,点C 、D是以线段 AB 为公共弦的两条圆弧的中点,AB = 4,点 E 、F 分别是线段CD、AB
AF = x, AE 2上的动点,设 EF
2 = y,则能表示 y 与 x 的函数关系的图像是( )
.
18. 小明新买了一辆自行车,说明书中关于轮胎的使用说明如下:小明看了说明书后,和爸爸讨论:
小明经过计算,得出这对轮胎能行驶的最长路程是( )
A. 9.8 千公里 B. 9.9 千公里 C. 3 11千公里 D. 10 千公里
第 2 页
三、解答题(8+10+10)
2
19. 如图,四边形 ABCD是菱形,点 D的坐标是 (0, 3),以点C 为顶点的抛物线 y = ax + bx + c 恰好
经过 x 轴上 A、 B 两点
(1)求 A、 B 、C 三点的坐标;
(2)求过 A、 B 、C 三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过 D点,求平移后抛物线的解析式,并指出平移了多少
个单位?
20. 已知 x 、 y 均为实数,且满足 xy + x + y = 17, x
2 y + xy2 = 66 ,
4
求:代数式 x + x
3 y + x2 y2 + xy3 + y4 的值
第 3 页
1 1 2
21. 已知:如图一次函数 y = x +1的图象与 x 轴交于点 A,与 y 轴交于点 B ;二次函数 y = x + bx + c
2 2
1
的图象与一次函数 y = x +1的图象交于 B 、C 两点,与 x 轴交于 D、 E 两点且 D点坐标为 (1,0)
2
(1)求二次函数的解析式;
(2)求四边形 BDEC 的面积 S ;
(3)在 x 轴上是否存在点 P ,使得 PBC 是以 P 为直角顶点的直角三角形?若存在,求出所有的点 P ,
若不存在,请说明理由
第 4 页
参考答案
一、填空题
5
1. 4 2. x 1 3. a + b 4. 20 5. 6. 6 7. 54 8. 21 或 9
5
l 2 2 2
9. 2 7 10. 11. a b = (a + b)(a b) 12. 小华
4
3 1 3
13. 14. (1)(2)(4)
4 2n +1 4
二、选择题
15. A 16. A 17. C 18. B
三、解答题
19. (1) A(1,0),B(3,0),C(2, 2);(2) y = 3(x 2)2 + 3 ;
(3) y = 3(x 2)2 +5 3,移动了 4 3 个单位
20. 109
1 3 1
21. (1) y = x2 x +1;(2) 4 ;(3)P(1,3) 或 (3,0)
2 2 2
第 5 页
一、填空题(每题 4 分)
2
1. 已知实数 x, y满足 x + 3x + y 3 = 0,则 x + y 的最大值为__________.
2. 直线 l1 : y = x +1与直线 l2 : y = mx + n相交于点 P(a,2),则m 2 时关于 x 的不等式 x+1 mx+ n
的解为__________.
3. 随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费标准按原标准每分钟降低了 a 元后,再次
下调了 25%,现在的收费标准是每分钟b 元,则原收费标准为__________元(用a,b表示)
2 2 b 1 a 1
4. 若实数 a b,且a,b满足a 8a + 5 = 0,b 8b + 5 = 0 ,则代数式 + 的值为__________.
a 1 b 1
5. 如图,已知直线 l1 / /l2 / /l3 / /l4 ,相邻两条平行直线间的距离都是 1,如果正方
形 ABCD的四个顶点分别在四条直线上,则 sin =__________.
6. 已知a+b+ c = 4,ab+bc+ ac = 5,则a2 +b2 + c2 = __________.
7. 商场的自动扶梯在匀速上升,一男孩与一女孩在这自动扶梯上往上爬,已知
男孩往上爬的速度是女孩往上爬的速度的 2 倍,男孩爬了 27 级到楼上,女孩爬
18 级到楼上,则从楼下到楼上自动扶梯的级数是__________.
8. 相交两圆的公共弦长为 16cm,若两圆的半径长分别为 10cm 和 17cm,则这
两圆的圆心距为__________cm
9. 如图,等边 ABC 的边长为 6, AD是 BC 边上的中线,M 是 AD上的动
点, E 是 AC 边上一点,若 AE = 2, EM +CM 的最小值为__________.
10. 用一长度为 l 的铁丝围成一个封闭图形,则其所围成的图形
的最大面积为__________.
11. 将图甲中阴影部分的小长方形变换到图乙位置,你能根据两
个图形的面积关系得到的数学公式是__________.
12. 在课外活动时间,小王、小丽、小华做“互相踢毽子”游戏,
毽子从一人传到另一人就记为踢一次,若经过三次踢毽后,毽子
踢到小王处的可能性最小,应从__________开始踢
13. 如图,n+1个上底、两腰长皆为 1,下底长为 2 的等腰梯形的下底均在同一直线上,设四边形 P1M1N1N2
面积为 S1 ,四边形 P2M 2N3N3 的面积为 S2 ,……,四边形 PnM nNnNn+1 的面积记为 Sn ,通过逐一计算
S1, S2 , ,可得 Sn = __________.
第 1 页
14. 如图,一次函数 y = ax+ b的图象与 x 轴,y 轴交于 A, B两点,与反比例函数
k
y = 的图象相交于C, D 两点,分别过C, D 两点作 y 轴, x 轴的垂线,垂足为
x
E,F ,连接CF,DE。有下列四个结论:
① CEF 与 DEF 的面积相等; ② AOB ∽ FOE ;
② DCE CDF ; ④ AC = BD
其中正确的结论是__________.
二、选择题(每题 4 分)
2
15. 已知抛物线 y = ax + bx + c(a 0)过 A( 2,0)、O(0,0) 、B( 3, y1) 、C(3, y2 ) 四点,则 y1 与 y2 的
大小关系是( )
A. y1 y2 B. y1 = y2 C. y1 y2 D. 不能确定
2 1
16. 运用图象法探索,方程 x x = 的解的情况是( )
x
A. 仅有一正根 B. 仅有一负根 C. 有一正根一负根 D. 无实根
17. 如图,点C 、D是以线段 AB 为公共弦的两条圆弧的中点,AB = 4,点 E 、F 分别是线段CD、AB
AF = x, AE 2上的动点,设 EF
2 = y,则能表示 y 与 x 的函数关系的图像是( )
.
18. 小明新买了一辆自行车,说明书中关于轮胎的使用说明如下:小明看了说明书后,和爸爸讨论:
小明经过计算,得出这对轮胎能行驶的最长路程是( )
A. 9.8 千公里 B. 9.9 千公里 C. 3 11千公里 D. 10 千公里
第 2 页
三、解答题(8+10+10)
2
19. 如图,四边形 ABCD是菱形,点 D的坐标是 (0, 3),以点C 为顶点的抛物线 y = ax + bx + c 恰好
经过 x 轴上 A、 B 两点
(1)求 A、 B 、C 三点的坐标;
(2)求过 A、 B 、C 三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过 D点,求平移后抛物线的解析式,并指出平移了多少
个单位?
20. 已知 x 、 y 均为实数,且满足 xy + x + y = 17, x
2 y + xy2 = 66 ,
4
求:代数式 x + x
3 y + x2 y2 + xy3 + y4 的值
第 3 页
1 1 2
21. 已知:如图一次函数 y = x +1的图象与 x 轴交于点 A,与 y 轴交于点 B ;二次函数 y = x + bx + c
2 2
1
的图象与一次函数 y = x +1的图象交于 B 、C 两点,与 x 轴交于 D、 E 两点且 D点坐标为 (1,0)
2
(1)求二次函数的解析式;
(2)求四边形 BDEC 的面积 S ;
(3)在 x 轴上是否存在点 P ,使得 PBC 是以 P 为直角顶点的直角三角形?若存在,求出所有的点 P ,
若不存在,请说明理由
第 4 页
参考答案
一、填空题
5
1. 4 2. x 1 3. a + b 4. 20 5. 6. 6 7. 54 8. 21 或 9
5
l 2 2 2
9. 2 7 10. 11. a b = (a + b)(a b) 12. 小华
4
3 1 3
13. 14. (1)(2)(4)
4 2n +1 4
二、选择题
15. A 16. A 17. C 18. B
三、解答题
19. (1) A(1,0),B(3,0),C(2, 2);(2) y = 3(x 2)2 + 3 ;
(3) y = 3(x 2)2 +5 3,移动了 4 3 个单位
20. 109
1 3 1
21. (1) y = x2 x +1;(2) 4 ;(3)P(1,3) 或 (3,0)
2 2 2
第 5 页
同课章节目录
