人教版数学九年级上册 23.2.3 关于原点对称的点的坐标 教学设计
文档属性
| 名称 | 人教版数学九年级上册 23.2.3 关于原点对称的点的坐标 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 44.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-13 16:31:04 | ||
图片预览

文档简介
23.2.3 关于原点对称的点的坐标
一、教学目标:
1.知识与技能(学习目标)
⑴ 掌握点P(x,y)关于原点的对称点P'(-x,-y)的运用.
⑵ 能运用关于原点对称的点的坐标的关系解决具体问题.
2.过程与方法
通过观察和操作,理解关于原点对称的点的坐标的关系,并会运用.
3.情感态度与价值观
通过观察、操作、交流、归纳等过程,培养学生探究问题的能力、动手能力、观察能力
以及与他人合作交流的能力.
二、教学重难点:
重点:关于原点对称的两个点的横坐标相反,纵坐标相反.
难点:利用特殊图形与特殊坐标之间的对应关系发展数形结合思想.
三、教学过程:
1.温故知新:
回忆所学过的直角坐标系中点关于X轴、Y轴对称的点的坐标关系,引出本节课的内容-----关于原点对称的点的关系
2.合作探究(一):
⑴教材68页的“探究”
通过利用前面学习的“中心对称”知识,作已知点关于原点的对称点,探究对称点间的坐标关系.
⑵归纳得出结论:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点 为P'(-x,-y)。
⑶练习: 做“ 找关于原点的对称点的 ”3个小练习
1.请直接说出下列各点关于原点的对称点的坐标 :
A(3,1) B(-2,3) C(-1,-2)
D(2,-3) E(-5,0) F(0,2)
2.若点P(x,-3)与点Q(4,y)关于原点对称,则x+y等于( )
A.1 B.-1 C.7 D.-7
3 .已知点A(-2m+4,3m-1)关于原点的对称点位于第三象限,则m的取值范围是( )
3.合作探究(二):
⑴教材68页的“例2”
关于原点对称的点的坐标的关系的应用:------利用关于原点对称的点的坐标关系,做出与△ABC关于原点对称的图形。
⑵练习:利用关于原点对称的点的坐标关系,做出关于原点对称的图形(线段、多边形)。
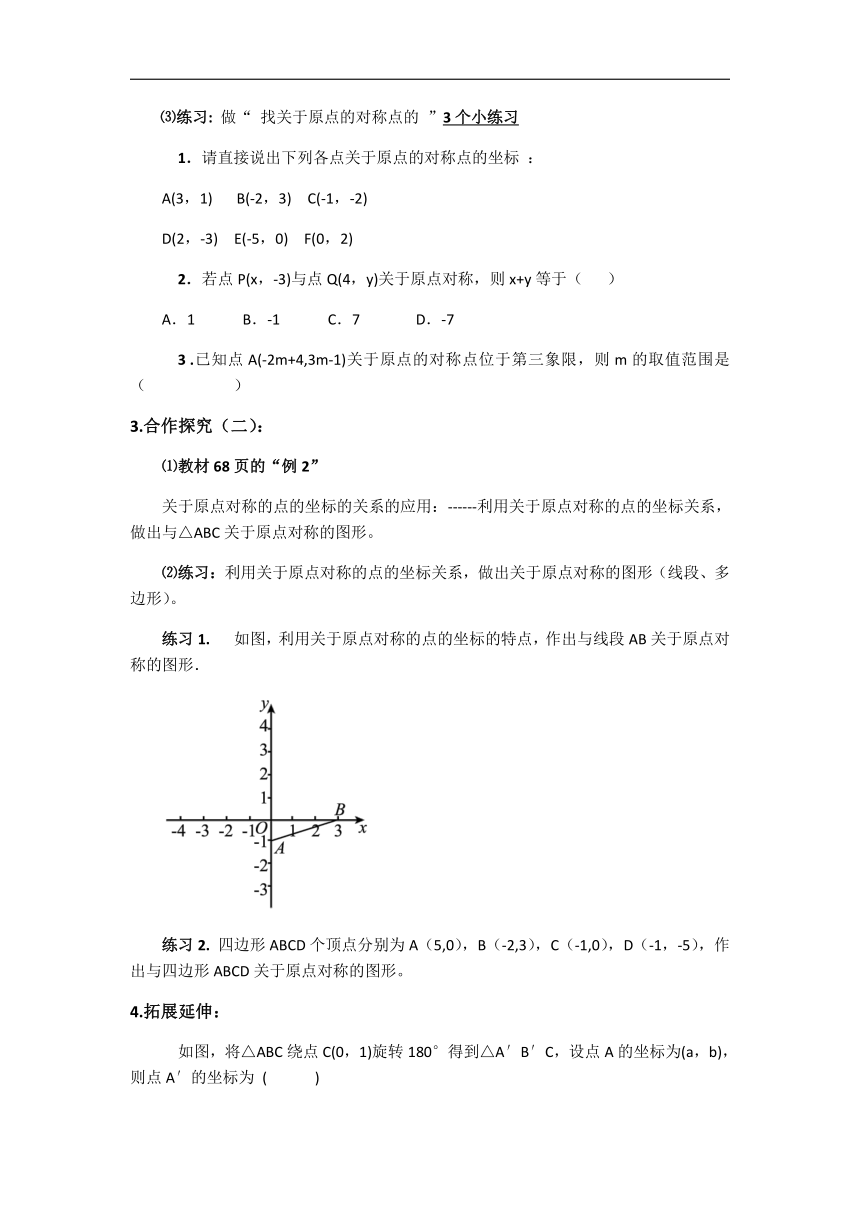
练习1. 如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
练习2. 四边形ABCD个顶点分别为A(5,0),B(-2,3),C(-1,0),D(-1,-5),作出与四边形ABCD关于原点对称的图形。
4.拓展延伸:
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为 ( )
A.(-a,-b) B.(-a,-b-1)
C.(-a,-b+1) D.(-a,-b+2)
四、课堂小结:
今天我们学习了:
1.关于原点对称的点的坐标特征;
两个点关于原点对称时,它们的坐标符号相反,即 点P(x,y)关于原点的对称点为P'(-x,-y).
2. 利用点的坐标确定字母的取值或范围;
3. 作一个图形关于原点对称的图形(如:线段、三角形、多边形等).
五、板书:
23.2.3关于原点对称的点的坐标
1.关于原点对称的点的坐标特征:
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点 为P'(-x,-y)。
2.关于原点对称点的坐标的应用:
六、教学反思:
学生已经学习了关于坐标轴对称的点的坐标,以及关于中心对称和中心对称作图的相关知识,因此本节课主要采用学生自主探究、观察发现、总结结论的方法来展开教学。通过教学,我总结了以下几点反思:
让学生自己动手操作,通过画中心对称图形找出关于原点对称的点的坐标并总结特点,是以学生为主体,充分发挥了学生的主体作用。
在课堂中仍有一部分学生实际操作能力不够,作图不到位。这部分学生由于基础薄弱,在学习中缺少自信心,课上及课后应多加以辅导、鼓励。
这节课基本按预设的完成了,学生通过探究、发现,总结出关于原点对称的点坐标特点,大部分学生积极性较高。
一、教学目标:
1.知识与技能(学习目标)
⑴ 掌握点P(x,y)关于原点的对称点P'(-x,-y)的运用.
⑵ 能运用关于原点对称的点的坐标的关系解决具体问题.
2.过程与方法
通过观察和操作,理解关于原点对称的点的坐标的关系,并会运用.
3.情感态度与价值观
通过观察、操作、交流、归纳等过程,培养学生探究问题的能力、动手能力、观察能力
以及与他人合作交流的能力.
二、教学重难点:
重点:关于原点对称的两个点的横坐标相反,纵坐标相反.
难点:利用特殊图形与特殊坐标之间的对应关系发展数形结合思想.
三、教学过程:
1.温故知新:
回忆所学过的直角坐标系中点关于X轴、Y轴对称的点的坐标关系,引出本节课的内容-----关于原点对称的点的关系
2.合作探究(一):
⑴教材68页的“探究”
通过利用前面学习的“中心对称”知识,作已知点关于原点的对称点,探究对称点间的坐标关系.
⑵归纳得出结论:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点 为P'(-x,-y)。
⑶练习: 做“ 找关于原点的对称点的 ”3个小练习
1.请直接说出下列各点关于原点的对称点的坐标 :
A(3,1) B(-2,3) C(-1,-2)
D(2,-3) E(-5,0) F(0,2)
2.若点P(x,-3)与点Q(4,y)关于原点对称,则x+y等于( )
A.1 B.-1 C.7 D.-7
3 .已知点A(-2m+4,3m-1)关于原点的对称点位于第三象限,则m的取值范围是( )
3.合作探究(二):
⑴教材68页的“例2”
关于原点对称的点的坐标的关系的应用:------利用关于原点对称的点的坐标关系,做出与△ABC关于原点对称的图形。
⑵练习:利用关于原点对称的点的坐标关系,做出关于原点对称的图形(线段、多边形)。
练习1. 如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
练习2. 四边形ABCD个顶点分别为A(5,0),B(-2,3),C(-1,0),D(-1,-5),作出与四边形ABCD关于原点对称的图形。
4.拓展延伸:
如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标为 ( )
A.(-a,-b) B.(-a,-b-1)
C.(-a,-b+1) D.(-a,-b+2)
四、课堂小结:
今天我们学习了:
1.关于原点对称的点的坐标特征;
两个点关于原点对称时,它们的坐标符号相反,即 点P(x,y)关于原点的对称点为P'(-x,-y).
2. 利用点的坐标确定字母的取值或范围;
3. 作一个图形关于原点对称的图形(如:线段、三角形、多边形等).
五、板书:
23.2.3关于原点对称的点的坐标
1.关于原点对称的点的坐标特征:
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点 为P'(-x,-y)。
2.关于原点对称点的坐标的应用:
六、教学反思:
学生已经学习了关于坐标轴对称的点的坐标,以及关于中心对称和中心对称作图的相关知识,因此本节课主要采用学生自主探究、观察发现、总结结论的方法来展开教学。通过教学,我总结了以下几点反思:
让学生自己动手操作,通过画中心对称图形找出关于原点对称的点的坐标并总结特点,是以学生为主体,充分发挥了学生的主体作用。
在课堂中仍有一部分学生实际操作能力不够,作图不到位。这部分学生由于基础薄弱,在学习中缺少自信心,课上及课后应多加以辅导、鼓励。
这节课基本按预设的完成了,学生通过探究、发现,总结出关于原点对称的点坐标特点,大部分学生积极性较高。
同课章节目录
