苏科版初中物理九年级(上)教学讲义11.5 机械效率(学生版+教师版)
文档属性
| 名称 | 苏科版初中物理九年级(上)教学讲义11.5 机械效率(学生版+教师版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-13 00:00:00 | ||
图片预览




文档简介
第十一章 简单机械和功
11.5 机械效率
【本节目标】
知道有用功、额外功、总功;
理解机械效率定义、大小范围、表示方法、公式、影响因素;
知道有用功、额外功、总功关系式;
理解机械效率的计算及公式。
题型汇总:机械效率的概念、机械效率大小的比较和计算、滑轮组的机械效率和实验、杠杆的机械效率和实验、斜面的机械效率和实验。
【知识要点】
有用功、额外功与总功
有用功:完成某项任务时有实用价值的功,即对人们有用的功。
额外功:对人没用但又不得不做的功。如:从井中打水时提水桶和绳子所做的功。
额外功产生的主要原因:提升重物时,克服机械自重、容器自重等所做的功,以及克服机械的摩擦所做的功。
总功:人们在达到一定目的的过程中,实际做的功,数值上等于有用功与额外功之和。
机械效率
定义:有用功与总功的比值。
公式:η= ×100%
η是一个没有单位的量,常用百分数表示。
机械效率是反映机械性能好坏的物理量,机械效率越高,这个机械的性能越好。机械效率只是反应有用功和总功的比值,只是一个比值关系,和做功多少、做功的距离、省力费力、做功快慢等因素无关;
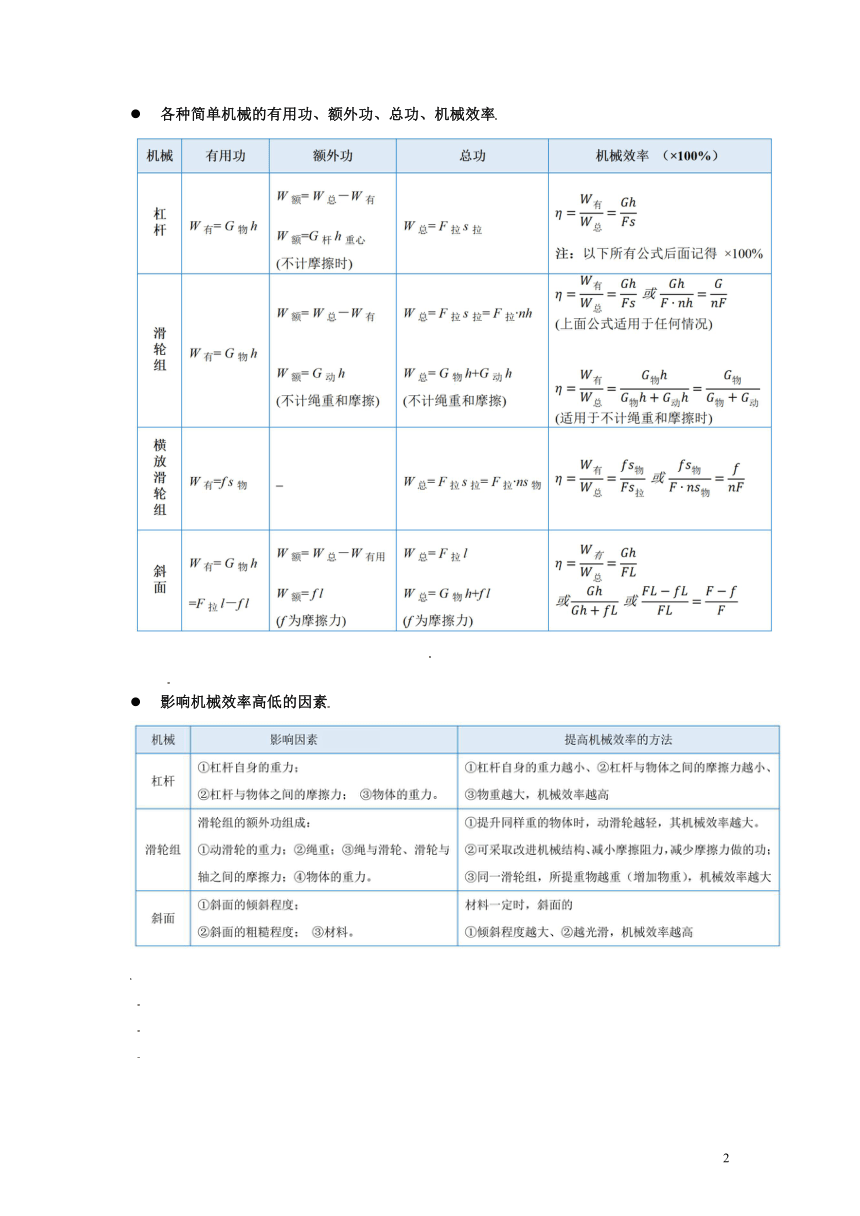
各种简单机械的有用功、额外功、总功、机械效率
影响机械效率高低的因素
【典题精选】
考点一 机械效率的概念
1.下列关于机械效率说法正确的是 ( )
A.机械做功越快,机械效率就越高
B.省力越多的机械,机械效率越大
C.单位时间做功越多的机械,效率越高
D.额外功在总功中占比例越小的机械效率越高
2.下列说法正确的是 ( )
A.机械效率高的机械,做功一定快
B.效率高的机械,做的有用功一定多
C.功率大的机械,做功一定快
D.功率大的机械,做功一定多
考点二 机械效率的大小比较
3.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为,机械效率为;用乙滑轮所做的总功为,机械效率为.若不计绳重与摩擦,则 ( )
4.两个完全相同的滑轮,其重力均为,分别用图甲、乙两种方式,将重的物体以相同的速度匀速竖直提升了,不计绳重和摩擦,则下列判断正确的是 ( )
A.做的功大于做的功 B.和做的功相等
C.做功的功率小于做功的功率 D.甲的机械效率小于乙的机械效率
5.如图为了提升重物,我们选用了粗细均匀重为的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在、两处,每次用力让杠杆上升同样的高度,下列说法正确是 ( )
A.重物在点处做的有用功多,机械效率高
B.重物在和点处杠杆的机械效率相等
C.重物在点处做的有用功多,杠杆的机械效率高
D.重物在点处做的额外功多,杠杆的机械效率高
考点三 机械效率的计算
6.小明不小心将水桶掉入井中,用钩子将质量为的桶从离井口的深处匀速捞到井口,称出桶内水的质量为,这次捞桶的过程中,做的有用功是 ,额外功是 ,总功是 ,机械效率为 取。
7.如图所示,搬运工人用滑轮组在内将重为的重物匀速提升,所用拉力为,则他拉力的功率是 ,滑轮组的机械效率是 。若定滑轮、动滑轮各增加一个组成新的滑轮组,将相同的重物提升相同的高度,机械效率将 (选填“增大”、“减小”或“不变”
8.如图所示,此图为“测量滑轮组机械效率”的实验装置,钩码总重力为,小明用的拉力竖直向上匀速拉动细线(绳重和摩擦忽略不计)。
(1)若钩码内上升,则钩码上升的速度为多少?
(2)小明拉力做功的功率是多少?该滑轮组的机械效率是多少?
(3)当钩码总重力为时,该滑轮组的机械效率为多大?(结果保留一位小数)
考点四 滑轮(组)的机械效率
9.如图所示,用滑轮组提升重物时,重的重物在内匀速上升了。已知拉绳子的力为,不计绳重和摩擦,则提升重物的过程中 ( )
A.绳子自由端下降速度为
B.动滑轮的重力为
C.拉力的功率是
D.滑轮组的机械效率是
10.某建筑工地上,一台起重机内将重的物体匀速提升,起重机吊臂上的滑轮组如图所示,滑轮组的机械效率为。下列分析错误的是 ( )
A.拉力的大小为 B.有用功的大小为
C.额外功的大小为 D.拉力的功率为
11.如图所示,用一个滑轮组匀速提升重为的物体,物体在内运动规律如图乙中图像,其中内拉绳的力为。
(1)在内所做的有用功是 ,滑轮组的机械效率是 。
(2)后,内继续拉绳,则拉力 ;滑轮组的机械效率 ;拉力的功率 。(均选填“变大”、“变小”或“不变” (不计绳重和摩擦)
考点五 滑轮(组)机械效率的测量实验
12.在“测量滑轮组的机械效率”实验中,小丽用同一滑轮组提升不同的物体,如图甲、乙所示,实验数据记录如下:
实验次数 物体重力 提升高度 拉力 绳端移动的距离 机械效率
1 3 0.1 2.0 0.3
2 6 0.1 ① 0.3 ②
(1)实验中要竖直向上 拉动弹簧测力计。
(2)图乙中弹簧测力计的示数为 ,表格中②处数据应为 。分析实验数据可知:滑轮组的机械效率和 有关。
(3)如图丙所示,将滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率 (选填“变大”、“不变”或“变小” 。
13.在“探究动滑轮工作时的特点”活动中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,在正确操作的情况下,测得的实验数据如下。
实验 序号 钩码重 钩码上升 高度 拉力 绳端移动的 距离
① 1.0 10 1.1 20
② 2.0 10 1.7 20
③ 3.0 10 2.3 20
(1)实验时,用手竖直向上 拉动弹簧测力计,读出弹簧测力计的示数。
(2)分析表中数据发现,使用动滑轮提升物体时,拉力不等于物体重力的一半,而是大于物体重力的一半,其主要原因是 。
(3)第①次实验中,动滑轮的机械效率为 (结果保留一位小数)。
(4)分析表中实验数据可知,同一动滑轮,所提升物重增大,机械效率将 (选填“增大”、“减小”或“不变” 。
(5)若在第③次实验中,不小心使钩码多上升了,但仍用表格中的数据进行计算,测得的机械效率将 (变大变小不变)。
(6)在某一次测量中,弹簧测力计不是沿竖直向上拉,而是斜向上拉,其他条件不变,动滑轮的机械效率将 (变大变小不变)。
考点六 杠杆的机械效率
14.小明用如图所示的装置研究“杠杆的机械效率”实验时,将重为的钩码挂在铁质杠杆上点,弹簧测力计作用于点,现竖直向上匀速拉动弹簧测力计,杠杆的机械效率;若仅将弹簧测力计改挂到点,仍将钩码竖直向上匀速提升的高度,杠杆的机械效率为,则 ( )
A. B. C. D.无法确定
15.如图所示,弹簧测力计的示数为 ,钩码的重力为,钩码上升的高度为,测力计竖直向上移动的距离为,此时杠杆的机械效率为 。忽略杠杆转动轴的摩擦,仅将钩码的悬挂点从移到,若重物提升高度相同,则额外功与有用功的比值将 (增大减小不变),杠杆的机械效率将 。(增大减小不变)
16.如图所示,工人用一均匀杠杆将重为的货物匀速提高,如果动力臂与阻力臂之比为,而工人所用的拉力为。则在此过程中杠杆的机械效率为 (保留一位小数),如果克服摩擦做功,则此杠杆的自重为 。
17.如图所示,在测定杠杆机械效率的实验中,竖直向上匀速拉动弹簧测力计,使挂在杠杆下面的物块缓慢上升至虚线位置,测力计的示数为 ,测力计上升的高度为,物块重为,物块上升的高度为,则杠杆的机械效率为 ,如果变大,此杠杆机械效率将变 。
18.如图所示,一根均匀的细木棒,,为的中点.在点用始终竖直向上的的拉力将挂在点的重为的物体匀速提升.提升该物体做的有用功是 ,总功是 ,木棒的机械效率为 ,木棒重为 (不计摩擦),如果将拉力从点移动至点,则机械效率会 (增加、不变或减小)
19.小明用如图所示的实验装置研究“杠杆的机械效率”。实验时,将总重为的钩码挂在杠杆上的点,用竖直向上的力拉弹簧测力计,使钩码上升,弹簧测力计移动的距离为,则杠杆的机械效率 ;若增加钩码的重量,重复实验,则杠杆的机械效率将 (变大变小不变);若钩码的重量不变,将弹簧测力计移动到点竖直向上拉,仍将钩码匀速提升相同的高度,设此时弹簧测力计的示数为,杠杆的机械效率为,若不计转轴处的摩擦,则: , 。
考点七 杠杆机械效率的测量实验
20.小明用如图所示的装置探究杠杆的机械效率,每个钩码的质量为,为支点。
(1)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,拉力为,测得、两点上升的高度分别为、,则此次杠杆的机械效率 (用物理量的符号表示)。
(2)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度为,则弹簧测力计的示数将 (大于小于等于,下同),此次弹簧测力计做的功将 第一次做的功。
(3)他将3只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度仍为,则第3次杠杆的机械效率与前两次相比 (选填“最大”、“最小”或“三次相等” 。
21.用如图所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数为 ,钩码总重为,钩码上升高度为,测力计移动距离为,则杠杆的机械效率为 .请写出使用该杠杆做额外功的一个原因: 。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在、两点,测量并计算得到下表所示的两组数据:
次数 钩码 悬挂点 钩码总重 钩码移动距离 拉力 测力计移动距离 机械效率
1 点 1.5 0.10 0.7 0.30 71.4
2 点 2.0 0.15 1.2 0.30 83.3
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答: ;
22.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升(支点和杠杆的摩擦不计)。问:
(1)重为的钩码挂在点时,人的拉力为,钩码上升时,动力作用点上升,此时有用功为 ,总功为 ,机械效率为 。
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到点,再次缓慢提升杠杆使动力作用点仍然上升。问:人的拉力与第一次相比 (选填“变大”、“变小”或“不变” ;有用功与第一次相比 (选填“变大”、“变小”或“不变” ;额外功与第一次相比 (选填“变大”、“变小”或“不变” ;比较此时的机械效率 (选填“大于”、“等于”或“小于” 。
考点八 斜面的机械效率
23.如图所示,斜面长,高,小明用绳子在内将重的物体从其底端沿斜面向上匀速拉到顶端,拉力是。下列说法中正确的是 ( )
A.斜面上的摩擦力是 B.拉力所做的功是
C.拉力做功的功率是 D.斜面的机械效率是
24.如图所示,将一个物体从斜面底端匀速拉到斜面顶端,沿斜面向上的拉力大小为,斜面长,假如不用斜面,直接把物体匀速竖直提升至相同的高度所做的功是,则斜面的机械效率为 ,物体在斜面上所受的摩擦力为 。
考点九 斜面机械效率的测量实验
25.某实验小组的同学们在探究“斜面的机械效率”实验时,用弹簧测力计沿斜面匀速向上拉动物块,收集了下表中的实验数据。
实验次数 斜面的倾 斜程度 物块重 力 斜面高 度 拉力 斜面长 度 机械效 率
1 较缓 5 0.2 2.4 1
2 较陡 5 0.5 3.2 1
3 最陡 5 0.7 4.3 1
(1)分析表中的数据可得出:斜面越缓越 力(选填“省”或“费” 。
(2)该小组又进行了第4次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是和,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为,他们测得这种情况下斜面的机械效率为 。
(3)把第4次实验数据与表中数据综合分析可得出:斜面的机械效率与 和 有关。
(4)当用弹簧测力计沿斜面匀速向上拉动物块时,物块所受的拉力 物块所受的摩擦力(选填“大于”、“小于”或“等于” 。
26.用图示装置探究“斜面机械效率”,实验记录如表。
实验次数 物体种类 物重 斜面高 沿斜面的拉力 斜面长 机械效率
1 木块 4 15 1.1 90 60.6
2 小车 4 15 90
(1)沿斜面拉动物体时,应使其做 运动。
(2)根据图示测力计的示数,拉力为 ,可知第2次实验的机械效率为 .由实验可得初步结论:斜面倾斜程度相同时, 越小,机械效率越大。
(3)第1次实验中,木块所受摩擦力为 。
第十一章 简单机械和功
11.5 机械效率
【本节目标】
知道有用功、额外功、总功;
理解机械效率定义、大小范围、表示方法、公式、影响因素;
知道有用功、额外功、总功关系式;
理解机械效率的计算及公式。
题型汇总:机械效率的概念、机械效率大小的比较和计算、滑轮组的机械效率和实验、杠杆的机械效率和实验、斜面的机械效率和实验。
【知识要点】
有用功、额外功与总功
有用功:完成某项任务时有实用价值的功,即对人们有用的功。
额外功:对人没用但又不得不做的功。如:从井中打水时提水桶和绳子所做的功。
额外功产生的主要原因:提升重物时,克服机械自重、容器自重等所做的功,以及克服机械的摩擦所做的功。
总功:人们在达到一定目的的过程中,实际做的功,数值上等于有用功与额外功之和。
机械效率
定义:有用功与总功的比值。
公式:η= ×100%
η是一个没有单位的量,常用百分数表示。
机械效率是反映机械性能好坏的物理量,机械效率越高,这个机械的性能越好。机械效率只是反应有用功和总功的比值,只是一个比值关系,和做功多少、做功的距离、省力费力、做功快慢等因素无关;
各种简单机械的有用功、额外功、总功、机械效率
影响机械效率高低的因素
【典题精选】
考点一 机械效率的概念
1.下列关于机械效率说法正确的是 ( )
A.机械做功越快,机械效率就越高
B.省力越多的机械,机械效率越大
C.单位时间做功越多的机械,效率越高
D.额外功在总功中占比例越小的机械效率越高
【解答】解:、机械做功越快,表示功率越大,单位时间内做的功越多,但机械效率不一定就高,故说法不对;
、机械效率是指有用功占总功的百分比,与是否省力没有必然的联系,故说法不对;
、单位时间做功越多,说明功率越大,与机械效率无关,故说法不对;
、总功包括有用功和额外功,额外功在总功中占比例越小,则有用功在总功中占比例越大,机械效率越高,故说法正确。
故选:。
2.下列说法正确的是 ( )
A.机械效率高的机械,做功一定快
B.效率高的机械,做的有用功一定多
C.功率大的机械,做功一定快
D.功率大的机械,做功一定多
【解答】解:、机械效率高,说明有用功与总功的比值大,做功不一定快,故错;
、因为机械效率是有用功与总功的比值,所以做功多的机械,其机械效率不一定高,故错;
、功率是表示做功快慢的物理量,做功越快的机械,功率一定越大,故正确;
、由公式可知,不知道做功时间的长短,无法判断做功的多少,故错。
故选:。
考点二 机械效率的大小比较
3.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为,机械效率为;用乙滑轮所做的总功为,机械效率为.若不计绳重与摩擦,则 ( )
【解答】解:
(1)因为小明分别用甲、乙两滑轮把同一袋沙从地面提到二楼,所以两种情况的有用功相同;
(2)当有用功一定时,乙中所做的总功为对一袋沙所做的功,利用机械时做的额外功越少,则总功就越少,机械效率就越高;
又因为甲是动滑轮,甲中所做的总功还要加上对动滑轮所做的功,利用甲滑轮做的额外功多,则总功越多,机械效率越低。即,。
故选:。
4.两个完全相同的滑轮,其重力均为,分别用图甲、乙两种方式,将重的物体以相同的速度匀速竖直提升了,不计绳重和摩擦,则下列判断正确的是 ( )
A.做的功大于做的功 B.和做的功相等
C.做功的功率小于做功的功率 D.甲的机械效率小于乙的机械效率
【解答】解:由图可知,甲图中拉力,而乙图中拉力为;
设物体上升了,则甲图中拉力作用的距离为;乙图中物体上升的高度为;
则做功;
做功;
故的功小于的功;故、错误;
的功率;
的功率;
故做功的功率小于做功的功率;故正确;
因甲中拉力的功等于克服重力的功,故甲中没有额外功,故机械效率为,而乙中由于要拉动动滑轮,故克服动滑轮重力所做的功为额外功;故甲的机械效率大于乙的机械效率;
故错误;
故选:。
5.如图为了提升重物,我们选用了粗细均匀重为的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在、两处,每次用力让杠杆上升同样的高度,下列说法正确是 ( )
A.重物在点处做的有用功多,机械效率高
B.重物在和点处杠杆的机械效率相等
C.重物在点处做的有用功多,杠杆的机械效率高
D.重物在点处做的额外功多,杠杆的机械效率高
【解答】解:(1)利用杠杆提升重物,
有用功,
在、两处提升的是同一个重物,每次杠杆上升同样的高度,而重物上升的高度,
在、两处人做的有用功不相同,重物在点处做的有用功少,故选项错误。
(2)由图可知:在、两处提升重物,每次用力让杠杆上升同样的高度,而杠杆的重心上升的高度,
额外功:,
,故错误;
在、两处人对重物提升的高度不同,做的有用功不相同,而,
,
由,
可得.所以选项错误,选项正确。
故选:。
考点三 机械效率的计算
6.小明不小心将水桶掉入井中,用钩子将质量为的桶从离井口的深处匀速捞到井口,称出桶内水的质量为,这次捞桶的过程中,做的有用功是 ,额外功是 ,总功是 ,机械效率为 取。
【解答】解:有用功为:;
该过程中是为了打捞水桶,对水桶中的水所做的功为额外功,额外功为:
总功为:
机械效率为:。
故答案为:50;450;500;。
7.如图所示,搬运工人用滑轮组在内将重为的重物匀速提升,所用拉力为,则他拉力的功率是 ,滑轮组的机械效率是 。若定滑轮、动滑轮各增加一个组成新的滑轮组,将相同的重物提升相同的高度,机械效率将 (选填“增大”、“减小”或“不变”
【解答】解:(1)滑轮组由3段绳子承担,则绳子移动距离为:;
拉力做功为:
;拉力的功率为:;
(2)有用功为:
;
机械效率为:
;
(3)若定滑轮、动滑轮各增加一个组成新的滑轮组,将相同的重物提升相同的高度;此过程中,有用功不变,但是额外功会变大,故机械效率将减小;
故答案为:90;;减小
8.如图所示,此图为“测量滑轮组机械效率”的实验装置,钩码总重力为,小明用的拉力竖直向上匀速拉动细线(绳重和摩擦忽略不计)。
(1)若钩码内上升,则钩码上升的速度为多少?
(2)小明拉力做功的功率是多少?该滑轮组的机械效率是多少?
(3)当钩码总重力为时,该滑轮组的机械效率为多大?(结果保留一位小数)
【解答】解:(1)若钩码内上升,则钩码上升的速度:;
(2)已知:钩码重力,拉力,,时间,高度,钩码总重
由滑轮组结构得出承担物重的绳子股数,则;
此时拉力做的功是:;
故此时的功率是:;
此时有用功是:,
故此时的机械效率是:;
(2)在不计绳重和摩擦的情况下,,
动滑轮的重力是:
,
此时滑轮组的机械效率为:
。
答:(1)钩码上升的速度为;
(2)小明拉力做功的功率;该滑轮组的机械效率是;
(3)当钩码总重力为时,该滑轮组的机械效率。
考点四 滑轮(组)的机械效率
9.如图所示,用滑轮组提升重物时,重的重物在内匀速上升了。已知拉绳子的力为,不计绳重和摩擦,则提升重物的过程中 ( )
A.绳子自由端下降速度为
B.动滑轮的重力为
C.拉力的功率是
D.滑轮组的机械效率是
【解答】解:
、由图知,,绳子自由端被拉下的距离:,
绳子自由端下降的速度:,故错误;
、不计绳重和摩擦,拉力,则动滑轮的重力:,故错误;
、拉力做的总功:,
拉力做功的功率:,故错误;
、拉力做的有用功:
,
滑轮组的机械效率:
,故正确。
故选:。
10.某建筑工地上,一台起重机内将重的物体匀速提升,起重机吊臂上的滑轮组如图所示,滑轮组的机械效率为。下列分析错误的是 ( )
A.拉力的大小为 B.有用功的大小为
C.额外功的大小为 D.拉力的功率为
【解答】解:滑轮组承担物重绳子段数:,
、有用功:,故正确;
由得,
总功:,
拉力移动距离:,由得,
拉力:;故错误;
、额外功:,正确;
、拉力功率:,故正确。
故选:。
11.如图所示,用一个滑轮组匀速提升重为的物体,物体在内运动规律如图乙中图像,其中内拉绳的力为。
(1)在内所做的有用功是 ,滑轮组的机械效率是 。
(2)后,内继续拉绳,则拉力 ;滑轮组的机械效率 ;拉力的功率 。(均选填“变大”、“变小”或“不变” (不计绳重和摩擦)
【解答】解:(1)由物体的图像可知,物体在、做匀速直线运动,
物体在的速度,
在的速度;
物体在内上升的高度:
,
在内拉力所做的有用功:
,
由图知,,拉力端移动距离,
拉力做的总功:
,
滑轮组的机械效率:
;
(2)不计绳重和摩擦,在内拉绳还是匀速拉动,因为拉力端移动的速度等于物体提升速度的2倍,所以拉力端移动速度减小;
而拉力,所以拉力大小不变,
由可知拉力功率变小;
拉力不变、提升物重不变,由可知滑轮组机械效率不变。
故答案为:(1)400;;(2)不变;不变;变小。
考点五 滑轮(组)机械效率的测量实验
12.在“测量滑轮组的机械效率”实验中,小丽用同一滑轮组提升不同的物体,如图甲、乙所示,实验数据记录如下:
实验次数 物体重力 提升高度 拉力 绳端移动的距离 机械效率
1 3 0.1 2.0 0.3
2 6 0.1 ① 0.3 ②
(1)实验中要竖直向上 拉动弹簧测力计。
(2)图乙中弹簧测力计的示数为 ,表格中②处数据应为 。分析实验数据可知:滑轮组的机械效率和 有关。
(3)如图丙所示,将滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率 (选填“变大”、“不变”或“变小” 。
【解答】解:
(1)实验中要竖直向上匀速拉动弹簧测力计,使钩码升高,此时整体处于平衡状态,测力计示数才等于拉力大小,同时也便于测出测力计的拉力;
(2)由图可知,测力计分度值为,示数为;
第2次实验的有用功:;
总功:,
则第2次的机械效率为:;
所以①处数据应为3.2,②处数据应为;
根据表格中的数据可知,用相同的滑轮组提升不同的重物,物体的重力越大,机械效率越高,即滑轮组的机械效率和物体的重力有关;
(3)若将此滑轮组换一种绕绳方法,不计摩擦及绳重,额外功的来源是克服动滑轮自重做的功,
额外功:,
有用功:,
总功:,
此时滑轮组的机械效率:,改变绕绳方法时,与均不变,由上式知,滑轮组的机械效率不变。
故答案为:(1)匀速;(2)3.2;62.5;物体的重力;(3)不变。
13.在“探究动滑轮工作时的特点”活动中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,在正确操作的情况下,测得的实验数据如下。
实验 序号 钩码重 钩码上升 高度 拉力 绳端移动的 距离
① 1.0 10 1.1 20
② 2.0 10 1.7 20
③ 3.0 10 2.3 20
(1)实验时,用手竖直向上 拉动弹簧测力计,读出弹簧测力计的示数。
(2)分析表中数据发现,使用动滑轮提升物体时,拉力不等于物体重力的一半,而是大于物体重力的一半,其主要原因是 。
(3)第①次实验中,动滑轮的机械效率为 (结果保留一位小数)。
(4)分析表中实验数据可知,同一动滑轮,所提升物重增大,机械效率将 (选填“增大”、“减小”或“不变” 。
(5)若在第③次实验中,不小心使钩码多上升了,但仍用表格中的数据进行计算,测得的机械效率将 (变大变小不变)。
(6)在某一次测量中,弹簧测力计不是沿竖直向上拉,而是斜向上拉,其他条件不变,动滑轮的机械效率将 (变大变小不变)。
【解答】解:(1)实验时,用手竖直向上缓慢匀速拉动弹簧测力计,此时系统处于平衡状态,测力计示数才等于拉力大小;读出弹簧测力计的示数;
(2)由可知,由于动滑轮有重力,所以拉力大于物体重力的一半;
(3)第①次实验中,,,
动滑轮的机械效率为:
;
(4)同理,第②③次实验的机械效率分别为和,故分析表中实验数据可知,同一动滑轮,所提升物重增大,机械效率将增大;
(5)本实验中,,因,与提升钩码上升的高度无关,若在第③次实验中,不小心使钩码多上升了,但仍用表格中的数据进行计算,测得的机械效率将不变;
(6)当拉力的方向不在竖直方向上时,由于动力臂变短,会造成拉力偏大,从而使得总功变大,根据,在有用功不变的情况下,总功增大,所以机械效率变小。
故答案为:(1)缓慢;匀速;(2)动滑轮有重力;(3);(4)增大;(5)不变;(6)变小。
考点六 杠杆的机械效率
14.小明用如图所示的装置研究“杠杆的机械效率”实验时,将重为的钩码挂在铁质杠杆上点,弹簧测力计作用于点,现竖直向上匀速拉动弹簧测力计,杠杆的机械效率;若仅将弹簧测力计改挂到点,仍将钩码竖直向上匀速提升的高度,杠杆的机械效率为,则 ( )
A. B. C. D.无法确定
【解答】解:
原来弹簧测力计作用于点,竖直向上匀速拉动弹簧测力计时,测得杠杆的机械效率;将弹簧测力计移动到点时,仍将钩码竖直向上匀速提升相同的高度,根据可知有用功不变;
因杠杆的偏转角度不变,则杠杆重心上升的高度不变,根据可知,克服杠杆重和摩擦所做额外功不变;由于有用功和额外功都不变,所以总功也不变,根据可知杠杆的机械效率不变,即。
故选:。
15.如图所示,弹簧测力计的示数为 ,钩码的重力为,钩码上升的高度为,测力计竖直向上移动的距离为,此时杠杆的机械效率为 。忽略杠杆转动轴的摩擦,仅将钩码的悬挂点从移到,若重物提升高度相同,则额外功与有用功的比值将 (增大减小不变),杠杆的机械效率将 。(增大减小不变)
【解答】解:
(1)由图可知,弹簧测力计的分度值是,所以它的示数是。
(2)在实验过程中,有用功是:,
总功是:,
所以杠杆的机械效率:;
(3)杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,并且;
设杠杆重心升高的距离为,所以,,不变,不变,不变,
钩码从点到点,钩码还升高相同的高度,有用功不变;
杠杆上旋的角度减小,杠杆升高的距离变小,克服杠杆重力所做的额外功变小,所以额外功与有用功的比值将减小;
因为变小,所以也变小;根据可知,总功变小,有用功不变,所以增大。
故答案为:0.5;;减小;增大。
16.如图所示,工人用一均匀杠杆将重为的货物匀速提高,如果动力臂与阻力臂之比为,而工人所用的拉力为。则在此过程中杠杆的机械效率为 (保留一位小数),如果克服摩擦做功,则此杠杆的自重为 。
【解答】解:
(1)有用功:;
由题知,动力臂与阻力臂之比为,即,
则动力移动距离是阻力移动距离的二倍,所以拉力移动的距离,
拉力做的总功:,
杠杆的机械效率:;
(2)根据可知,拉力做的额外功:
,
已知克服摩擦做功,克服杠杆自重做的额外功:
,
由可知杠杆自重:
。
故答案为:;160。
17.如图所示,在测定杠杆机械效率的实验中,竖直向上匀速拉动弹簧测力计,使挂在杠杆下面的物块缓慢上升至虚线位置,测力计的示数为 ,测力计上升的高度为,物块重为,物块上升的高度为,则杠杆的机械效率为 ,如果变大,此杠杆机械效率将变 。
【解答】解:(1)由图可知,弹簧测力计的分度值是,测力计的示数为;
(2)有用功:;
总功:;
则杠杆的机械效率:。
(3)在阻力一定的情况下,物重越大,有用功占总功的比值越大,杠杆的机械效率越大。
所以,如果变大,此杠杆机械效率将变大。
故答案为:2.5;90;大。
18.如图所示,一根均匀的细木棒,,为的中点.在点用始终竖直向上的的拉力将挂在点的重为的物体匀速提升.提升该物体做的有用功是 ,总功是 ,木棒的机械效率为 ,木棒重为 (不计摩擦),如果将拉力从点移动至点,则机械效率会 (增加、不变或减小)
【解答】解:(1)提升该物体做的有用功:
;
(2)因为,所以;
提升该物体做的总功:
;
由;
(3)因为,
所以,克服木棒重力做的额外功:
,
因为,为的中点,所以;
所以,由相似三角形的知识可知,当物体上升时,点(重心)将上升;
不计摩擦和绳子重,由可得木棒重力:
。
(4)根据图示可知,将拉力从点移动至点,提升高度变小,点上升的高度变小,故有用功减小,额外功减小,总功减小,根据可知,机械效率不变。
故答案为:18;20;;10;不变。
19.小明用如图所示的实验装置研究“杠杆的机械效率”。实验时,将总重为的钩码挂在杠杆上的点,用竖直向上的力拉弹簧测力计,使钩码上升,弹簧测力计移动的距离为,则杠杆的机械效率 ;若增加钩码的重量,重复实验,则杠杆的机械效率将 (变大变小不变);若钩码的重量不变,将弹簧测力计移动到点竖直向上拉,仍将钩码匀速提升相同的高度,设此时弹簧测力计的示数为,杠杆的机械效率为,若不计转轴处的摩擦,则: , 。
【解答】解:(1)的钩码挂在杠杆上,现竖直向上匀速拉动弹簧测力计,钩码上升的高度为,弹簧测力计的示数为,其移动的距离为,
杠杆的机械效率:
;
(2)若增加钩码的重量,重复实验,因不计转轴处的摩擦,克服铁质杠杆重力做的功为额外功,则有用功增大,额外功不变,根据,则杠杆的机械效率将变大;
(3)根据原图示可知,若钩码的重量不变,将弹簧测力计移动到点时,阻力和阻力臂都不变,动力臂减小,由可知,动力将增大,即;
不计转轴处的摩擦,克服杠杆重力做的功为额外功,仍将钩码匀速提升的高度,由于有用功和额外功均不变,则总功也不变,根据,故机械效率不变,即。
故答案为:;变大;;。
考点七 杠杆机械效率的测量实验
20.小明用如图所示的装置探究杠杆的机械效率,每个钩码的质量为,为支点。
(1)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,拉力为,测得、两点上升的高度分别为、,则此次杠杆的机械效率 (用物理量的符号表示)。
(2)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度为,则弹簧测力计的示数将 (大于小于等于,下同),此次弹簧测力计做的功将 第一次做的功。
(3)他将3只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度仍为,则第3次杠杆的机械效率与前两次相比 (选填“最大”、“最小”或“三次相等” 。
【解答】解:(1)有用功为,总功,则机械效率的表达式。
(2)钩码的悬挂点在点时,由杠杆的平衡条件得;悬挂点移至点时,由杠杆的平衡条件得;从图中可以看出,由到力臂变大,所以弹簧测力计的示数变大,有用功不变,但杠杆提升的高度减小,额外功减小,又因为总功等于额外功与有用功之和,因此此次弹簧测力计做的功将小于第一次做的功。
(3)因为第1与第2的有用功相等,并且第2的额外功小,因为机械效率等于有用功与总功的比值,因此第1的机械效率小于第2的机械效率;
将3只钩码悬挂在点时,物体升高的高度不变,物重增加,由可得,有用功变大,但杠杆提升的高度与第2相同,额外功与第2相同,又因为机械效率等于有用功与总功的比值,因此第3的机械效率大于第2的机械效率。
综上所述,第3的机械效率最大。
故答案为:(1);(2)大于;小于;(3)最大。
21.用如图所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数为 ,钩码总重为,钩码上升高度为,测力计移动距离为,则杠杆的机械效率为 .请写出使用该杠杆做额外功的一个原因: 。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在、两点,测量并计算得到下表所示的两组数据:
次数 钩码 悬挂点 钩码总重 钩码移动距离 拉力 测力计移动距离 机械效率
1 点 1.5 0.10 0.7 0.30 71.4
2 点 2.0 0.15 1.2 0.30 83.3
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答: ;
【解答】解:(1)弹簧测力计每一个大格代表,每一个小格代表,指针超过5个小格,示数为;
用杠杆提起货物,对货物做的功是有用功,,
用杠杆提起货物,对整个杠杆做的功是总功,。
所以杠杆的机械效率:;
额外功产生的原因:克服机械的重做功、克服摩擦做功。
(2)题中悬挂点不同,物体的重力不同,变量不唯一,不能探究:“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”。
故答案为:(1)0.5;66.7;由于使用杠杆时需要克服杠杆自重做功;(2)不能。
22.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升(支点和杠杆的摩擦不计)。问:
(1)重为的钩码挂在点时,人的拉力为,钩码上升时,动力作用点上升,此时有用功为 ,总功为 ,机械效率为 。
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到点,再次缓慢提升杠杆使动力作用点仍然上升。问:人的拉力与第一次相比 (选填“变大”、“变小”或“不变” ;有用功与第一次相比 (选填“变大”、“变小”或“不变” ;额外功与第一次相比 (选填“变大”、“变小”或“不变” ;比较此时的机械效率 (选填“大于”、“等于”或“小于” 。
【解答】解:(1)有用功:;
总功:,
机械效率:;
(2)钩码的悬挂点在点时,由于杠杆的重力会阻碍杠杆转动,
则由杠杆的平衡条件得:;
悬挂点移至点时,由杠杆的平衡条件得,
观察比较可知,悬挂点移至点时,,即钩码重力的力臂变小,所以拉力也变小;
杠杆的机械效率:;
因为杠杆升高的高度不变,所以克服杠杆自重所做的额外功不变(即不变);由于悬挂点更接近支点,所以钩码提升的高度减小,根据可知,有用功减小;
从上面的表达式可知:减小、不变,所以变大,分母变大,就减小;即。
故答案为:(1)1.5;2;;
(2)变小;变小;不变;小于。
考点八 斜面的机械效率
23.如图所示,斜面长,高,小明用绳子在内将重的物体从其底端沿斜面向上匀速拉到顶端,拉力是。下列说法中正确的是 ( )
A.斜面上的摩擦力是 B.拉力所做的功是
C.拉力做功的功率是 D.斜面的机械效率是
【解答】解:(1)此过程所做有用功为:;
拉力所做总功为:;
故机械效率为:;
(2)拉力做功的功率为:;
(3)此过程所做额外功为:;
由变形得:
摩擦力为:。
故错误,正确。
故选:。
24.如图所示,将一个物体从斜面底端匀速拉到斜面顶端,沿斜面向上的拉力大小为,斜面长,假如不用斜面,直接把物体匀速竖直提升至相同的高度所做的功是,则斜面的机械效率为 ,物体在斜面上所受的摩擦力为 。
【解答】解:
(1)拉力做的有用功:,
拉力做的总功:,
斜面的机械效率:
;
(2)拉力做的额外功:
,
因为,
所以摩擦力大小:
。
故答案为:83.3;5。
考点九 斜面机械效率的测量实验
25.某实验小组的同学们在探究“斜面的机械效率”实验时,用弹簧测力计沿斜面匀速向上拉动物块,收集了下表中的实验数据。
实验次数 斜面的倾 斜程度 物块重 力 斜面高 度 拉力 斜面长 度 机械效 率
1 较缓 5 0.2 2.4 1
2 较陡 5 0.5 3.2 1
3 最陡 5 0.7 4.3 1
(1)分析表中的数据可得出:斜面越缓越 力(选填“省”或“费” 。
(2)该小组又进行了第4次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是和,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为,他们测得这种情况下斜面的机械效率为 。
(3)把第4次实验数据与表中数据综合分析可得出:斜面的机械效率与 和 有关。
(4)当用弹簧测力计沿斜面匀速向上拉动物块时,物块所受的拉力 物块所受的摩擦力(选填“大于”、“小于”或“等于” 。
【解答】解:(1)分析表中第二列与第五列对比斜面坡度与沿斜面拉力的变化情况可知,斜面越缓越越省力。
(2)这种情况下斜面的机械效率:
。
(3)分析表格中的第二列和第七列可知斜面的机械效率与倾斜程度有关,分析第2次和第4次实验数据可知斜面的机械效率与接触面的粗糙程度有关;
故斜面的机械效率与斜面倾斜程度和斜面粗糙程度有关。
(4)实验过程中,用弹簧测力计的拉力要同时克服摩擦力和物体的一部分重力,所以。
故答案为:(1)省; (2);(3)斜面倾斜程度;斜面粗糙程度; (4)大于。
26.用图示装置探究“斜面机械效率”,实验记录如表。
实验次数 物体种类 物重 斜面高 沿斜面的拉力 斜面长 机械效率
1 木块 4 15 1.1 90 60.6
2 小车 4 15 90
(1)沿斜面拉动物体时,应使其做 运动。
(2)根据图示测力计的示数,拉力为 ,可知第2次实验的机械效率为 .由实验可得初步结论:斜面倾斜程度相同时, 越小,机械效率越大。
(3)第1次实验中,木块所受摩擦力为 。
【解答】解:
(1)沿斜面拉动物体时,为使弹簧测力计的示数稳定,便于读数,所以应尽量使物体做匀速直线运动;
(2)由图可知:弹簧测力计的分度值为,示数为,
则第2次实验斜面的机械效率;
比较两次的机械效率可知,第2次机械效率大,斜面的倾斜程度相同,小车所受的摩擦力小,由此可得结论:斜面倾斜程度相同时,摩擦力越小,机械效率越大;
(3)由第1次实验的数据可知,
沿斜面拉木块做的有用功,
拉力做的总功,
则额外功,
由得,木块所受摩擦力。
故答案为:(1)匀速直线;(2)0.7;95.2;摩擦力;(3)0.43。
11.5 机械效率
【本节目标】
知道有用功、额外功、总功;
理解机械效率定义、大小范围、表示方法、公式、影响因素;
知道有用功、额外功、总功关系式;
理解机械效率的计算及公式。
题型汇总:机械效率的概念、机械效率大小的比较和计算、滑轮组的机械效率和实验、杠杆的机械效率和实验、斜面的机械效率和实验。
【知识要点】
有用功、额外功与总功
有用功:完成某项任务时有实用价值的功,即对人们有用的功。
额外功:对人没用但又不得不做的功。如:从井中打水时提水桶和绳子所做的功。
额外功产生的主要原因:提升重物时,克服机械自重、容器自重等所做的功,以及克服机械的摩擦所做的功。
总功:人们在达到一定目的的过程中,实际做的功,数值上等于有用功与额外功之和。
机械效率
定义:有用功与总功的比值。
公式:η= ×100%
η是一个没有单位的量,常用百分数表示。
机械效率是反映机械性能好坏的物理量,机械效率越高,这个机械的性能越好。机械效率只是反应有用功和总功的比值,只是一个比值关系,和做功多少、做功的距离、省力费力、做功快慢等因素无关;
各种简单机械的有用功、额外功、总功、机械效率
影响机械效率高低的因素
【典题精选】
考点一 机械效率的概念
1.下列关于机械效率说法正确的是 ( )
A.机械做功越快,机械效率就越高
B.省力越多的机械,机械效率越大
C.单位时间做功越多的机械,效率越高
D.额外功在总功中占比例越小的机械效率越高
2.下列说法正确的是 ( )
A.机械效率高的机械,做功一定快
B.效率高的机械,做的有用功一定多
C.功率大的机械,做功一定快
D.功率大的机械,做功一定多
考点二 机械效率的大小比较
3.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为,机械效率为;用乙滑轮所做的总功为,机械效率为.若不计绳重与摩擦,则 ( )
4.两个完全相同的滑轮,其重力均为,分别用图甲、乙两种方式,将重的物体以相同的速度匀速竖直提升了,不计绳重和摩擦,则下列判断正确的是 ( )
A.做的功大于做的功 B.和做的功相等
C.做功的功率小于做功的功率 D.甲的机械效率小于乙的机械效率
5.如图为了提升重物,我们选用了粗细均匀重为的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在、两处,每次用力让杠杆上升同样的高度,下列说法正确是 ( )
A.重物在点处做的有用功多,机械效率高
B.重物在和点处杠杆的机械效率相等
C.重物在点处做的有用功多,杠杆的机械效率高
D.重物在点处做的额外功多,杠杆的机械效率高
考点三 机械效率的计算
6.小明不小心将水桶掉入井中,用钩子将质量为的桶从离井口的深处匀速捞到井口,称出桶内水的质量为,这次捞桶的过程中,做的有用功是 ,额外功是 ,总功是 ,机械效率为 取。
7.如图所示,搬运工人用滑轮组在内将重为的重物匀速提升,所用拉力为,则他拉力的功率是 ,滑轮组的机械效率是 。若定滑轮、动滑轮各增加一个组成新的滑轮组,将相同的重物提升相同的高度,机械效率将 (选填“增大”、“减小”或“不变”
8.如图所示,此图为“测量滑轮组机械效率”的实验装置,钩码总重力为,小明用的拉力竖直向上匀速拉动细线(绳重和摩擦忽略不计)。
(1)若钩码内上升,则钩码上升的速度为多少?
(2)小明拉力做功的功率是多少?该滑轮组的机械效率是多少?
(3)当钩码总重力为时,该滑轮组的机械效率为多大?(结果保留一位小数)
考点四 滑轮(组)的机械效率
9.如图所示,用滑轮组提升重物时,重的重物在内匀速上升了。已知拉绳子的力为,不计绳重和摩擦,则提升重物的过程中 ( )
A.绳子自由端下降速度为
B.动滑轮的重力为
C.拉力的功率是
D.滑轮组的机械效率是
10.某建筑工地上,一台起重机内将重的物体匀速提升,起重机吊臂上的滑轮组如图所示,滑轮组的机械效率为。下列分析错误的是 ( )
A.拉力的大小为 B.有用功的大小为
C.额外功的大小为 D.拉力的功率为
11.如图所示,用一个滑轮组匀速提升重为的物体,物体在内运动规律如图乙中图像,其中内拉绳的力为。
(1)在内所做的有用功是 ,滑轮组的机械效率是 。
(2)后,内继续拉绳,则拉力 ;滑轮组的机械效率 ;拉力的功率 。(均选填“变大”、“变小”或“不变” (不计绳重和摩擦)
考点五 滑轮(组)机械效率的测量实验
12.在“测量滑轮组的机械效率”实验中,小丽用同一滑轮组提升不同的物体,如图甲、乙所示,实验数据记录如下:
实验次数 物体重力 提升高度 拉力 绳端移动的距离 机械效率
1 3 0.1 2.0 0.3
2 6 0.1 ① 0.3 ②
(1)实验中要竖直向上 拉动弹簧测力计。
(2)图乙中弹簧测力计的示数为 ,表格中②处数据应为 。分析实验数据可知:滑轮组的机械效率和 有关。
(3)如图丙所示,将滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率 (选填“变大”、“不变”或“变小” 。
13.在“探究动滑轮工作时的特点”活动中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,在正确操作的情况下,测得的实验数据如下。
实验 序号 钩码重 钩码上升 高度 拉力 绳端移动的 距离
① 1.0 10 1.1 20
② 2.0 10 1.7 20
③ 3.0 10 2.3 20
(1)实验时,用手竖直向上 拉动弹簧测力计,读出弹簧测力计的示数。
(2)分析表中数据发现,使用动滑轮提升物体时,拉力不等于物体重力的一半,而是大于物体重力的一半,其主要原因是 。
(3)第①次实验中,动滑轮的机械效率为 (结果保留一位小数)。
(4)分析表中实验数据可知,同一动滑轮,所提升物重增大,机械效率将 (选填“增大”、“减小”或“不变” 。
(5)若在第③次实验中,不小心使钩码多上升了,但仍用表格中的数据进行计算,测得的机械效率将 (变大变小不变)。
(6)在某一次测量中,弹簧测力计不是沿竖直向上拉,而是斜向上拉,其他条件不变,动滑轮的机械效率将 (变大变小不变)。
考点六 杠杆的机械效率
14.小明用如图所示的装置研究“杠杆的机械效率”实验时,将重为的钩码挂在铁质杠杆上点,弹簧测力计作用于点,现竖直向上匀速拉动弹簧测力计,杠杆的机械效率;若仅将弹簧测力计改挂到点,仍将钩码竖直向上匀速提升的高度,杠杆的机械效率为,则 ( )
A. B. C. D.无法确定
15.如图所示,弹簧测力计的示数为 ,钩码的重力为,钩码上升的高度为,测力计竖直向上移动的距离为,此时杠杆的机械效率为 。忽略杠杆转动轴的摩擦,仅将钩码的悬挂点从移到,若重物提升高度相同,则额外功与有用功的比值将 (增大减小不变),杠杆的机械效率将 。(增大减小不变)
16.如图所示,工人用一均匀杠杆将重为的货物匀速提高,如果动力臂与阻力臂之比为,而工人所用的拉力为。则在此过程中杠杆的机械效率为 (保留一位小数),如果克服摩擦做功,则此杠杆的自重为 。
17.如图所示,在测定杠杆机械效率的实验中,竖直向上匀速拉动弹簧测力计,使挂在杠杆下面的物块缓慢上升至虚线位置,测力计的示数为 ,测力计上升的高度为,物块重为,物块上升的高度为,则杠杆的机械效率为 ,如果变大,此杠杆机械效率将变 。
18.如图所示,一根均匀的细木棒,,为的中点.在点用始终竖直向上的的拉力将挂在点的重为的物体匀速提升.提升该物体做的有用功是 ,总功是 ,木棒的机械效率为 ,木棒重为 (不计摩擦),如果将拉力从点移动至点,则机械效率会 (增加、不变或减小)
19.小明用如图所示的实验装置研究“杠杆的机械效率”。实验时,将总重为的钩码挂在杠杆上的点,用竖直向上的力拉弹簧测力计,使钩码上升,弹簧测力计移动的距离为,则杠杆的机械效率 ;若增加钩码的重量,重复实验,则杠杆的机械效率将 (变大变小不变);若钩码的重量不变,将弹簧测力计移动到点竖直向上拉,仍将钩码匀速提升相同的高度,设此时弹簧测力计的示数为,杠杆的机械效率为,若不计转轴处的摩擦,则: , 。
考点七 杠杆机械效率的测量实验
20.小明用如图所示的装置探究杠杆的机械效率,每个钩码的质量为,为支点。
(1)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,拉力为,测得、两点上升的高度分别为、,则此次杠杆的机械效率 (用物理量的符号表示)。
(2)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度为,则弹簧测力计的示数将 (大于小于等于,下同),此次弹簧测力计做的功将 第一次做的功。
(3)他将3只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度仍为,则第3次杠杆的机械效率与前两次相比 (选填“最大”、“最小”或“三次相等” 。
21.用如图所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数为 ,钩码总重为,钩码上升高度为,测力计移动距离为,则杠杆的机械效率为 .请写出使用该杠杆做额外功的一个原因: 。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在、两点,测量并计算得到下表所示的两组数据:
次数 钩码 悬挂点 钩码总重 钩码移动距离 拉力 测力计移动距离 机械效率
1 点 1.5 0.10 0.7 0.30 71.4
2 点 2.0 0.15 1.2 0.30 83.3
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答: ;
22.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升(支点和杠杆的摩擦不计)。问:
(1)重为的钩码挂在点时,人的拉力为,钩码上升时,动力作用点上升,此时有用功为 ,总功为 ,机械效率为 。
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到点,再次缓慢提升杠杆使动力作用点仍然上升。问:人的拉力与第一次相比 (选填“变大”、“变小”或“不变” ;有用功与第一次相比 (选填“变大”、“变小”或“不变” ;额外功与第一次相比 (选填“变大”、“变小”或“不变” ;比较此时的机械效率 (选填“大于”、“等于”或“小于” 。
考点八 斜面的机械效率
23.如图所示,斜面长,高,小明用绳子在内将重的物体从其底端沿斜面向上匀速拉到顶端,拉力是。下列说法中正确的是 ( )
A.斜面上的摩擦力是 B.拉力所做的功是
C.拉力做功的功率是 D.斜面的机械效率是
24.如图所示,将一个物体从斜面底端匀速拉到斜面顶端,沿斜面向上的拉力大小为,斜面长,假如不用斜面,直接把物体匀速竖直提升至相同的高度所做的功是,则斜面的机械效率为 ,物体在斜面上所受的摩擦力为 。
考点九 斜面机械效率的测量实验
25.某实验小组的同学们在探究“斜面的机械效率”实验时,用弹簧测力计沿斜面匀速向上拉动物块,收集了下表中的实验数据。
实验次数 斜面的倾 斜程度 物块重 力 斜面高 度 拉力 斜面长 度 机械效 率
1 较缓 5 0.2 2.4 1
2 较陡 5 0.5 3.2 1
3 最陡 5 0.7 4.3 1
(1)分析表中的数据可得出:斜面越缓越 力(选填“省”或“费” 。
(2)该小组又进行了第4次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是和,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为,他们测得这种情况下斜面的机械效率为 。
(3)把第4次实验数据与表中数据综合分析可得出:斜面的机械效率与 和 有关。
(4)当用弹簧测力计沿斜面匀速向上拉动物块时,物块所受的拉力 物块所受的摩擦力(选填“大于”、“小于”或“等于” 。
26.用图示装置探究“斜面机械效率”,实验记录如表。
实验次数 物体种类 物重 斜面高 沿斜面的拉力 斜面长 机械效率
1 木块 4 15 1.1 90 60.6
2 小车 4 15 90
(1)沿斜面拉动物体时,应使其做 运动。
(2)根据图示测力计的示数,拉力为 ,可知第2次实验的机械效率为 .由实验可得初步结论:斜面倾斜程度相同时, 越小,机械效率越大。
(3)第1次实验中,木块所受摩擦力为 。
第十一章 简单机械和功
11.5 机械效率
【本节目标】
知道有用功、额外功、总功;
理解机械效率定义、大小范围、表示方法、公式、影响因素;
知道有用功、额外功、总功关系式;
理解机械效率的计算及公式。
题型汇总:机械效率的概念、机械效率大小的比较和计算、滑轮组的机械效率和实验、杠杆的机械效率和实验、斜面的机械效率和实验。
【知识要点】
有用功、额外功与总功
有用功:完成某项任务时有实用价值的功,即对人们有用的功。
额外功:对人没用但又不得不做的功。如:从井中打水时提水桶和绳子所做的功。
额外功产生的主要原因:提升重物时,克服机械自重、容器自重等所做的功,以及克服机械的摩擦所做的功。
总功:人们在达到一定目的的过程中,实际做的功,数值上等于有用功与额外功之和。
机械效率
定义:有用功与总功的比值。
公式:η= ×100%
η是一个没有单位的量,常用百分数表示。
机械效率是反映机械性能好坏的物理量,机械效率越高,这个机械的性能越好。机械效率只是反应有用功和总功的比值,只是一个比值关系,和做功多少、做功的距离、省力费力、做功快慢等因素无关;
各种简单机械的有用功、额外功、总功、机械效率
影响机械效率高低的因素
【典题精选】
考点一 机械效率的概念
1.下列关于机械效率说法正确的是 ( )
A.机械做功越快,机械效率就越高
B.省力越多的机械,机械效率越大
C.单位时间做功越多的机械,效率越高
D.额外功在总功中占比例越小的机械效率越高
【解答】解:、机械做功越快,表示功率越大,单位时间内做的功越多,但机械效率不一定就高,故说法不对;
、机械效率是指有用功占总功的百分比,与是否省力没有必然的联系,故说法不对;
、单位时间做功越多,说明功率越大,与机械效率无关,故说法不对;
、总功包括有用功和额外功,额外功在总功中占比例越小,则有用功在总功中占比例越大,机械效率越高,故说法正确。
故选:。
2.下列说法正确的是 ( )
A.机械效率高的机械,做功一定快
B.效率高的机械,做的有用功一定多
C.功率大的机械,做功一定快
D.功率大的机械,做功一定多
【解答】解:、机械效率高,说明有用功与总功的比值大,做功不一定快,故错;
、因为机械效率是有用功与总功的比值,所以做功多的机械,其机械效率不一定高,故错;
、功率是表示做功快慢的物理量,做功越快的机械,功率一定越大,故正确;
、由公式可知,不知道做功时间的长短,无法判断做功的多少,故错。
故选:。
考点二 机械效率的大小比较
3.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为,机械效率为;用乙滑轮所做的总功为,机械效率为.若不计绳重与摩擦,则 ( )
【解答】解:
(1)因为小明分别用甲、乙两滑轮把同一袋沙从地面提到二楼,所以两种情况的有用功相同;
(2)当有用功一定时,乙中所做的总功为对一袋沙所做的功,利用机械时做的额外功越少,则总功就越少,机械效率就越高;
又因为甲是动滑轮,甲中所做的总功还要加上对动滑轮所做的功,利用甲滑轮做的额外功多,则总功越多,机械效率越低。即,。
故选:。
4.两个完全相同的滑轮,其重力均为,分别用图甲、乙两种方式,将重的物体以相同的速度匀速竖直提升了,不计绳重和摩擦,则下列判断正确的是 ( )
A.做的功大于做的功 B.和做的功相等
C.做功的功率小于做功的功率 D.甲的机械效率小于乙的机械效率
【解答】解:由图可知,甲图中拉力,而乙图中拉力为;
设物体上升了,则甲图中拉力作用的距离为;乙图中物体上升的高度为;
则做功;
做功;
故的功小于的功;故、错误;
的功率;
的功率;
故做功的功率小于做功的功率;故正确;
因甲中拉力的功等于克服重力的功,故甲中没有额外功,故机械效率为,而乙中由于要拉动动滑轮,故克服动滑轮重力所做的功为额外功;故甲的机械效率大于乙的机械效率;
故错误;
故选:。
5.如图为了提升重物,我们选用了粗细均匀重为的杠杆,不计杠杆支点处的摩擦,先后把同一个重物挂在、两处,每次用力让杠杆上升同样的高度,下列说法正确是 ( )
A.重物在点处做的有用功多,机械效率高
B.重物在和点处杠杆的机械效率相等
C.重物在点处做的有用功多,杠杆的机械效率高
D.重物在点处做的额外功多,杠杆的机械效率高
【解答】解:(1)利用杠杆提升重物,
有用功,
在、两处提升的是同一个重物,每次杠杆上升同样的高度,而重物上升的高度,
在、两处人做的有用功不相同,重物在点处做的有用功少,故选项错误。
(2)由图可知:在、两处提升重物,每次用力让杠杆上升同样的高度,而杠杆的重心上升的高度,
额外功:,
,故错误;
在、两处人对重物提升的高度不同,做的有用功不相同,而,
,
由,
可得.所以选项错误,选项正确。
故选:。
考点三 机械效率的计算
6.小明不小心将水桶掉入井中,用钩子将质量为的桶从离井口的深处匀速捞到井口,称出桶内水的质量为,这次捞桶的过程中,做的有用功是 ,额外功是 ,总功是 ,机械效率为 取。
【解答】解:有用功为:;
该过程中是为了打捞水桶,对水桶中的水所做的功为额外功,额外功为:
总功为:
机械效率为:。
故答案为:50;450;500;。
7.如图所示,搬运工人用滑轮组在内将重为的重物匀速提升,所用拉力为,则他拉力的功率是 ,滑轮组的机械效率是 。若定滑轮、动滑轮各增加一个组成新的滑轮组,将相同的重物提升相同的高度,机械效率将 (选填“增大”、“减小”或“不变”
【解答】解:(1)滑轮组由3段绳子承担,则绳子移动距离为:;
拉力做功为:
;拉力的功率为:;
(2)有用功为:
;
机械效率为:
;
(3)若定滑轮、动滑轮各增加一个组成新的滑轮组,将相同的重物提升相同的高度;此过程中,有用功不变,但是额外功会变大,故机械效率将减小;
故答案为:90;;减小
8.如图所示,此图为“测量滑轮组机械效率”的实验装置,钩码总重力为,小明用的拉力竖直向上匀速拉动细线(绳重和摩擦忽略不计)。
(1)若钩码内上升,则钩码上升的速度为多少?
(2)小明拉力做功的功率是多少?该滑轮组的机械效率是多少?
(3)当钩码总重力为时,该滑轮组的机械效率为多大?(结果保留一位小数)
【解答】解:(1)若钩码内上升,则钩码上升的速度:;
(2)已知:钩码重力,拉力,,时间,高度,钩码总重
由滑轮组结构得出承担物重的绳子股数,则;
此时拉力做的功是:;
故此时的功率是:;
此时有用功是:,
故此时的机械效率是:;
(2)在不计绳重和摩擦的情况下,,
动滑轮的重力是:
,
此时滑轮组的机械效率为:
。
答:(1)钩码上升的速度为;
(2)小明拉力做功的功率;该滑轮组的机械效率是;
(3)当钩码总重力为时,该滑轮组的机械效率。
考点四 滑轮(组)的机械效率
9.如图所示,用滑轮组提升重物时,重的重物在内匀速上升了。已知拉绳子的力为,不计绳重和摩擦,则提升重物的过程中 ( )
A.绳子自由端下降速度为
B.动滑轮的重力为
C.拉力的功率是
D.滑轮组的机械效率是
【解答】解:
、由图知,,绳子自由端被拉下的距离:,
绳子自由端下降的速度:,故错误;
、不计绳重和摩擦,拉力,则动滑轮的重力:,故错误;
、拉力做的总功:,
拉力做功的功率:,故错误;
、拉力做的有用功:
,
滑轮组的机械效率:
,故正确。
故选:。
10.某建筑工地上,一台起重机内将重的物体匀速提升,起重机吊臂上的滑轮组如图所示,滑轮组的机械效率为。下列分析错误的是 ( )
A.拉力的大小为 B.有用功的大小为
C.额外功的大小为 D.拉力的功率为
【解答】解:滑轮组承担物重绳子段数:,
、有用功:,故正确;
由得,
总功:,
拉力移动距离:,由得,
拉力:;故错误;
、额外功:,正确;
、拉力功率:,故正确。
故选:。
11.如图所示,用一个滑轮组匀速提升重为的物体,物体在内运动规律如图乙中图像,其中内拉绳的力为。
(1)在内所做的有用功是 ,滑轮组的机械效率是 。
(2)后,内继续拉绳,则拉力 ;滑轮组的机械效率 ;拉力的功率 。(均选填“变大”、“变小”或“不变” (不计绳重和摩擦)
【解答】解:(1)由物体的图像可知,物体在、做匀速直线运动,
物体在的速度,
在的速度;
物体在内上升的高度:
,
在内拉力所做的有用功:
,
由图知,,拉力端移动距离,
拉力做的总功:
,
滑轮组的机械效率:
;
(2)不计绳重和摩擦,在内拉绳还是匀速拉动,因为拉力端移动的速度等于物体提升速度的2倍,所以拉力端移动速度减小;
而拉力,所以拉力大小不变,
由可知拉力功率变小;
拉力不变、提升物重不变,由可知滑轮组机械效率不变。
故答案为:(1)400;;(2)不变;不变;变小。
考点五 滑轮(组)机械效率的测量实验
12.在“测量滑轮组的机械效率”实验中,小丽用同一滑轮组提升不同的物体,如图甲、乙所示,实验数据记录如下:
实验次数 物体重力 提升高度 拉力 绳端移动的距离 机械效率
1 3 0.1 2.0 0.3
2 6 0.1 ① 0.3 ②
(1)实验中要竖直向上 拉动弹簧测力计。
(2)图乙中弹簧测力计的示数为 ,表格中②处数据应为 。分析实验数据可知:滑轮组的机械效率和 有关。
(3)如图丙所示,将滑轮组换一种绕绳方法,不计摩擦及绳重,提升相同的物体时,滑轮组的机械效率 (选填“变大”、“不变”或“变小” 。
【解答】解:
(1)实验中要竖直向上匀速拉动弹簧测力计,使钩码升高,此时整体处于平衡状态,测力计示数才等于拉力大小,同时也便于测出测力计的拉力;
(2)由图可知,测力计分度值为,示数为;
第2次实验的有用功:;
总功:,
则第2次的机械效率为:;
所以①处数据应为3.2,②处数据应为;
根据表格中的数据可知,用相同的滑轮组提升不同的重物,物体的重力越大,机械效率越高,即滑轮组的机械效率和物体的重力有关;
(3)若将此滑轮组换一种绕绳方法,不计摩擦及绳重,额外功的来源是克服动滑轮自重做的功,
额外功:,
有用功:,
总功:,
此时滑轮组的机械效率:,改变绕绳方法时,与均不变,由上式知,滑轮组的机械效率不变。
故答案为:(1)匀速;(2)3.2;62.5;物体的重力;(3)不变。
13.在“探究动滑轮工作时的特点”活动中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,在正确操作的情况下,测得的实验数据如下。
实验 序号 钩码重 钩码上升 高度 拉力 绳端移动的 距离
① 1.0 10 1.1 20
② 2.0 10 1.7 20
③ 3.0 10 2.3 20
(1)实验时,用手竖直向上 拉动弹簧测力计,读出弹簧测力计的示数。
(2)分析表中数据发现,使用动滑轮提升物体时,拉力不等于物体重力的一半,而是大于物体重力的一半,其主要原因是 。
(3)第①次实验中,动滑轮的机械效率为 (结果保留一位小数)。
(4)分析表中实验数据可知,同一动滑轮,所提升物重增大,机械效率将 (选填“增大”、“减小”或“不变” 。
(5)若在第③次实验中,不小心使钩码多上升了,但仍用表格中的数据进行计算,测得的机械效率将 (变大变小不变)。
(6)在某一次测量中,弹簧测力计不是沿竖直向上拉,而是斜向上拉,其他条件不变,动滑轮的机械效率将 (变大变小不变)。
【解答】解:(1)实验时,用手竖直向上缓慢匀速拉动弹簧测力计,此时系统处于平衡状态,测力计示数才等于拉力大小;读出弹簧测力计的示数;
(2)由可知,由于动滑轮有重力,所以拉力大于物体重力的一半;
(3)第①次实验中,,,
动滑轮的机械效率为:
;
(4)同理,第②③次实验的机械效率分别为和,故分析表中实验数据可知,同一动滑轮,所提升物重增大,机械效率将增大;
(5)本实验中,,因,与提升钩码上升的高度无关,若在第③次实验中,不小心使钩码多上升了,但仍用表格中的数据进行计算,测得的机械效率将不变;
(6)当拉力的方向不在竖直方向上时,由于动力臂变短,会造成拉力偏大,从而使得总功变大,根据,在有用功不变的情况下,总功增大,所以机械效率变小。
故答案为:(1)缓慢;匀速;(2)动滑轮有重力;(3);(4)增大;(5)不变;(6)变小。
考点六 杠杆的机械效率
14.小明用如图所示的装置研究“杠杆的机械效率”实验时,将重为的钩码挂在铁质杠杆上点,弹簧测力计作用于点,现竖直向上匀速拉动弹簧测力计,杠杆的机械效率;若仅将弹簧测力计改挂到点,仍将钩码竖直向上匀速提升的高度,杠杆的机械效率为,则 ( )
A. B. C. D.无法确定
【解答】解:
原来弹簧测力计作用于点,竖直向上匀速拉动弹簧测力计时,测得杠杆的机械效率;将弹簧测力计移动到点时,仍将钩码竖直向上匀速提升相同的高度,根据可知有用功不变;
因杠杆的偏转角度不变,则杠杆重心上升的高度不变,根据可知,克服杠杆重和摩擦所做额外功不变;由于有用功和额外功都不变,所以总功也不变,根据可知杠杆的机械效率不变,即。
故选:。
15.如图所示,弹簧测力计的示数为 ,钩码的重力为,钩码上升的高度为,测力计竖直向上移动的距离为,此时杠杆的机械效率为 。忽略杠杆转动轴的摩擦,仅将钩码的悬挂点从移到,若重物提升高度相同,则额外功与有用功的比值将 (增大减小不变),杠杆的机械效率将 。(增大减小不变)
【解答】解:
(1)由图可知,弹簧测力计的分度值是,所以它的示数是。
(2)在实验过程中,有用功是:,
总功是:,
所以杠杆的机械效率:;
(3)杠杆提升钩码时,对钩码做有用功,克服杠杆重做额外功,并且;
设杠杆重心升高的距离为,所以,,不变,不变,不变,
钩码从点到点,钩码还升高相同的高度,有用功不变;
杠杆上旋的角度减小,杠杆升高的距离变小,克服杠杆重力所做的额外功变小,所以额外功与有用功的比值将减小;
因为变小,所以也变小;根据可知,总功变小,有用功不变,所以增大。
故答案为:0.5;;减小;增大。
16.如图所示,工人用一均匀杠杆将重为的货物匀速提高,如果动力臂与阻力臂之比为,而工人所用的拉力为。则在此过程中杠杆的机械效率为 (保留一位小数),如果克服摩擦做功,则此杠杆的自重为 。
【解答】解:
(1)有用功:;
由题知,动力臂与阻力臂之比为,即,
则动力移动距离是阻力移动距离的二倍,所以拉力移动的距离,
拉力做的总功:,
杠杆的机械效率:;
(2)根据可知,拉力做的额外功:
,
已知克服摩擦做功,克服杠杆自重做的额外功:
,
由可知杠杆自重:
。
故答案为:;160。
17.如图所示,在测定杠杆机械效率的实验中,竖直向上匀速拉动弹簧测力计,使挂在杠杆下面的物块缓慢上升至虚线位置,测力计的示数为 ,测力计上升的高度为,物块重为,物块上升的高度为,则杠杆的机械效率为 ,如果变大,此杠杆机械效率将变 。
【解答】解:(1)由图可知,弹簧测力计的分度值是,测力计的示数为;
(2)有用功:;
总功:;
则杠杆的机械效率:。
(3)在阻力一定的情况下,物重越大,有用功占总功的比值越大,杠杆的机械效率越大。
所以,如果变大,此杠杆机械效率将变大。
故答案为:2.5;90;大。
18.如图所示,一根均匀的细木棒,,为的中点.在点用始终竖直向上的的拉力将挂在点的重为的物体匀速提升.提升该物体做的有用功是 ,总功是 ,木棒的机械效率为 ,木棒重为 (不计摩擦),如果将拉力从点移动至点,则机械效率会 (增加、不变或减小)
【解答】解:(1)提升该物体做的有用功:
;
(2)因为,所以;
提升该物体做的总功:
;
由;
(3)因为,
所以,克服木棒重力做的额外功:
,
因为,为的中点,所以;
所以,由相似三角形的知识可知,当物体上升时,点(重心)将上升;
不计摩擦和绳子重,由可得木棒重力:
。
(4)根据图示可知,将拉力从点移动至点,提升高度变小,点上升的高度变小,故有用功减小,额外功减小,总功减小,根据可知,机械效率不变。
故答案为:18;20;;10;不变。
19.小明用如图所示的实验装置研究“杠杆的机械效率”。实验时,将总重为的钩码挂在杠杆上的点,用竖直向上的力拉弹簧测力计,使钩码上升,弹簧测力计移动的距离为,则杠杆的机械效率 ;若增加钩码的重量,重复实验,则杠杆的机械效率将 (变大变小不变);若钩码的重量不变,将弹簧测力计移动到点竖直向上拉,仍将钩码匀速提升相同的高度,设此时弹簧测力计的示数为,杠杆的机械效率为,若不计转轴处的摩擦,则: , 。
【解答】解:(1)的钩码挂在杠杆上,现竖直向上匀速拉动弹簧测力计,钩码上升的高度为,弹簧测力计的示数为,其移动的距离为,
杠杆的机械效率:
;
(2)若增加钩码的重量,重复实验,因不计转轴处的摩擦,克服铁质杠杆重力做的功为额外功,则有用功增大,额外功不变,根据,则杠杆的机械效率将变大;
(3)根据原图示可知,若钩码的重量不变,将弹簧测力计移动到点时,阻力和阻力臂都不变,动力臂减小,由可知,动力将增大,即;
不计转轴处的摩擦,克服杠杆重力做的功为额外功,仍将钩码匀速提升的高度,由于有用功和额外功均不变,则总功也不变,根据,故机械效率不变,即。
故答案为:;变大;;。
考点七 杠杆机械效率的测量实验
20.小明用如图所示的装置探究杠杆的机械效率,每个钩码的质量为,为支点。
(1)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,拉力为,测得、两点上升的高度分别为、,则此次杠杆的机械效率 (用物理量的符号表示)。
(2)他将2只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度为,则弹簧测力计的示数将 (大于小于等于,下同),此次弹簧测力计做的功将 第一次做的功。
(3)他将3只钩码悬挂在点,在点竖直向上匀速拉动弹簧测力计,使点上升高度仍为,则第3次杠杆的机械效率与前两次相比 (选填“最大”、“最小”或“三次相等” 。
【解答】解:(1)有用功为,总功,则机械效率的表达式。
(2)钩码的悬挂点在点时,由杠杆的平衡条件得;悬挂点移至点时,由杠杆的平衡条件得;从图中可以看出,由到力臂变大,所以弹簧测力计的示数变大,有用功不变,但杠杆提升的高度减小,额外功减小,又因为总功等于额外功与有用功之和,因此此次弹簧测力计做的功将小于第一次做的功。
(3)因为第1与第2的有用功相等,并且第2的额外功小,因为机械效率等于有用功与总功的比值,因此第1的机械效率小于第2的机械效率;
将3只钩码悬挂在点时,物体升高的高度不变,物重增加,由可得,有用功变大,但杠杆提升的高度与第2相同,额外功与第2相同,又因为机械效率等于有用功与总功的比值,因此第3的机械效率大于第2的机械效率。
综上所述,第3的机械效率最大。
故答案为:(1);(2)大于;小于;(3)最大。
21.用如图所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)实验中,将杠杆拉至图中虚线位置,测力计的示数为 ,钩码总重为,钩码上升高度为,测力计移动距离为,则杠杆的机械效率为 .请写出使用该杠杆做额外功的一个原因: 。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一位同学用该实验装置,先后将钩码挂在、两点,测量并计算得到下表所示的两组数据:
次数 钩码 悬挂点 钩码总重 钩码移动距离 拉力 测力计移动距离 机械效率
1 点 1.5 0.10 0.7 0.30 71.4
2 点 2.0 0.15 1.2 0.30 83.3
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”的结论?答: ;
【解答】解:(1)弹簧测力计每一个大格代表,每一个小格代表,指针超过5个小格,示数为;
用杠杆提起货物,对货物做的功是有用功,,
用杠杆提起货物,对整个杠杆做的功是总功,。
所以杠杆的机械效率:;
额外功产生的原因:克服机械的重做功、克服摩擦做功。
(2)题中悬挂点不同,物体的重力不同,变量不唯一,不能探究:“杠杆的机械效率与所挂钩码的重有关,钩码越重其效率越高”。
故答案为:(1)0.5;66.7;由于使用杠杆时需要克服杠杆自重做功;(2)不能。
22.小金用如图所示的实验装置测量杠杆的机械效率。实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升(支点和杠杆的摩擦不计)。问:
(1)重为的钩码挂在点时,人的拉力为,钩码上升时,动力作用点上升,此时有用功为 ,总功为 ,机械效率为 。
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到点,再次缓慢提升杠杆使动力作用点仍然上升。问:人的拉力与第一次相比 (选填“变大”、“变小”或“不变” ;有用功与第一次相比 (选填“变大”、“变小”或“不变” ;额外功与第一次相比 (选填“变大”、“变小”或“不变” ;比较此时的机械效率 (选填“大于”、“等于”或“小于” 。
【解答】解:(1)有用功:;
总功:,
机械效率:;
(2)钩码的悬挂点在点时,由于杠杆的重力会阻碍杠杆转动,
则由杠杆的平衡条件得:;
悬挂点移至点时,由杠杆的平衡条件得,
观察比较可知,悬挂点移至点时,,即钩码重力的力臂变小,所以拉力也变小;
杠杆的机械效率:;
因为杠杆升高的高度不变,所以克服杠杆自重所做的额外功不变(即不变);由于悬挂点更接近支点,所以钩码提升的高度减小,根据可知,有用功减小;
从上面的表达式可知:减小、不变,所以变大,分母变大,就减小;即。
故答案为:(1)1.5;2;;
(2)变小;变小;不变;小于。
考点八 斜面的机械效率
23.如图所示,斜面长,高,小明用绳子在内将重的物体从其底端沿斜面向上匀速拉到顶端,拉力是。下列说法中正确的是 ( )
A.斜面上的摩擦力是 B.拉力所做的功是
C.拉力做功的功率是 D.斜面的机械效率是
【解答】解:(1)此过程所做有用功为:;
拉力所做总功为:;
故机械效率为:;
(2)拉力做功的功率为:;
(3)此过程所做额外功为:;
由变形得:
摩擦力为:。
故错误,正确。
故选:。
24.如图所示,将一个物体从斜面底端匀速拉到斜面顶端,沿斜面向上的拉力大小为,斜面长,假如不用斜面,直接把物体匀速竖直提升至相同的高度所做的功是,则斜面的机械效率为 ,物体在斜面上所受的摩擦力为 。
【解答】解:
(1)拉力做的有用功:,
拉力做的总功:,
斜面的机械效率:
;
(2)拉力做的额外功:
,
因为,
所以摩擦力大小:
。
故答案为:83.3;5。
考点九 斜面机械效率的测量实验
25.某实验小组的同学们在探究“斜面的机械效率”实验时,用弹簧测力计沿斜面匀速向上拉动物块,收集了下表中的实验数据。
实验次数 斜面的倾 斜程度 物块重 力 斜面高 度 拉力 斜面长 度 机械效 率
1 较缓 5 0.2 2.4 1
2 较陡 5 0.5 3.2 1
3 最陡 5 0.7 4.3 1
(1)分析表中的数据可得出:斜面越缓越 力(选填“省”或“费” 。
(2)该小组又进行了第4次实验,他们在斜面上铺上棉布,使斜面变粗糙,保持斜面高和长分别是和,用弹簧测力计拉动同一物块沿斜面向上做匀速直线运动,读出此时弹簧测力计的示数为,他们测得这种情况下斜面的机械效率为 。
(3)把第4次实验数据与表中数据综合分析可得出:斜面的机械效率与 和 有关。
(4)当用弹簧测力计沿斜面匀速向上拉动物块时,物块所受的拉力 物块所受的摩擦力(选填“大于”、“小于”或“等于” 。
【解答】解:(1)分析表中第二列与第五列对比斜面坡度与沿斜面拉力的变化情况可知,斜面越缓越越省力。
(2)这种情况下斜面的机械效率:
。
(3)分析表格中的第二列和第七列可知斜面的机械效率与倾斜程度有关,分析第2次和第4次实验数据可知斜面的机械效率与接触面的粗糙程度有关;
故斜面的机械效率与斜面倾斜程度和斜面粗糙程度有关。
(4)实验过程中,用弹簧测力计的拉力要同时克服摩擦力和物体的一部分重力,所以。
故答案为:(1)省; (2);(3)斜面倾斜程度;斜面粗糙程度; (4)大于。
26.用图示装置探究“斜面机械效率”,实验记录如表。
实验次数 物体种类 物重 斜面高 沿斜面的拉力 斜面长 机械效率
1 木块 4 15 1.1 90 60.6
2 小车 4 15 90
(1)沿斜面拉动物体时,应使其做 运动。
(2)根据图示测力计的示数,拉力为 ,可知第2次实验的机械效率为 .由实验可得初步结论:斜面倾斜程度相同时, 越小,机械效率越大。
(3)第1次实验中,木块所受摩擦力为 。
【解答】解:
(1)沿斜面拉动物体时,为使弹簧测力计的示数稳定,便于读数,所以应尽量使物体做匀速直线运动;
(2)由图可知:弹簧测力计的分度值为,示数为,
则第2次实验斜面的机械效率;
比较两次的机械效率可知,第2次机械效率大,斜面的倾斜程度相同,小车所受的摩擦力小,由此可得结论:斜面倾斜程度相同时,摩擦力越小,机械效率越大;
(3)由第1次实验的数据可知,
沿斜面拉木块做的有用功,
拉力做的总功,
则额外功,
由得,木块所受摩擦力。
故答案为:(1)匀速直线;(2)0.7;95.2;摩擦力;(3)0.43。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
