人教版七年级上册 1.5.1 有理数的乘方 优质课件(共20张PPT)
文档属性
| 名称 | 人教版七年级上册 1.5.1 有理数的乘方 优质课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 20:56:58 | ||
图片预览






文档简介
(共20张PPT)
1.5 有理数的乘方
第一章 有理数
国王和大臣
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。第1格放2粒,第2格放4粒米,第3格放8粒米,然后是16粒、32粒、64粒……一直到第64格。”“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!” 你认为国王的国库里有这么多米吗
复习提问:
1.5.1 有理数的乘方
几个不是0的有理数相乘,积的符号是由什么确定的?
积的符号是由负因数的个数确定的,
当负因数的个数为偶数时,积的符号为正;
当负因数的个数为奇数时,积的符号为负.
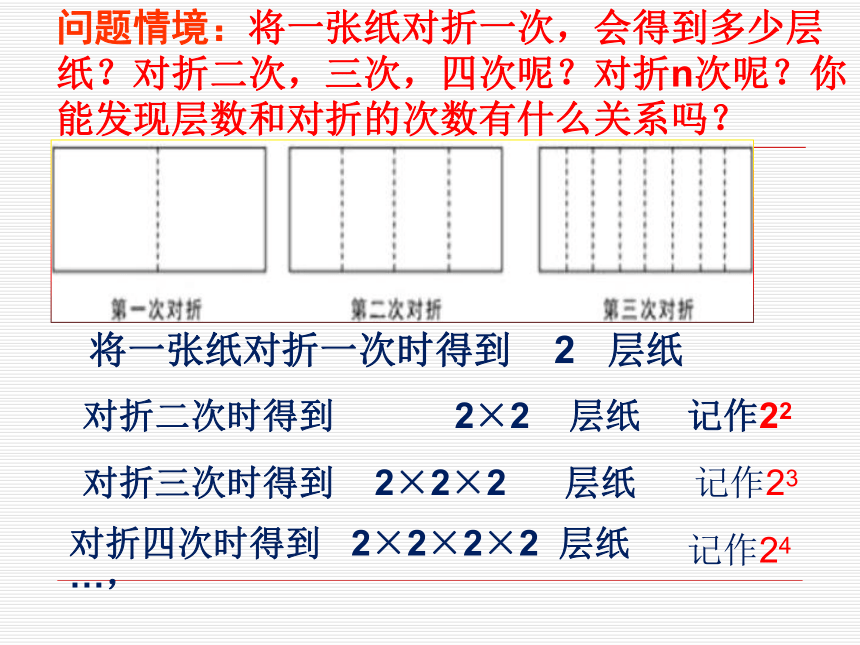
问题情境:将一张纸对折一次,会得到多少层纸?对折二次,三次,四次呢?对折n次呢?你能发现层数和对折的次数有什么关系吗?
将一张纸对折一次时得到 2 层纸
对折二次时得到 2×2 层纸
对折四次时得到 2×2×2×2 层纸
对折三次时得到 2×2×2 层纸
…,
记作22
记作23
记作24
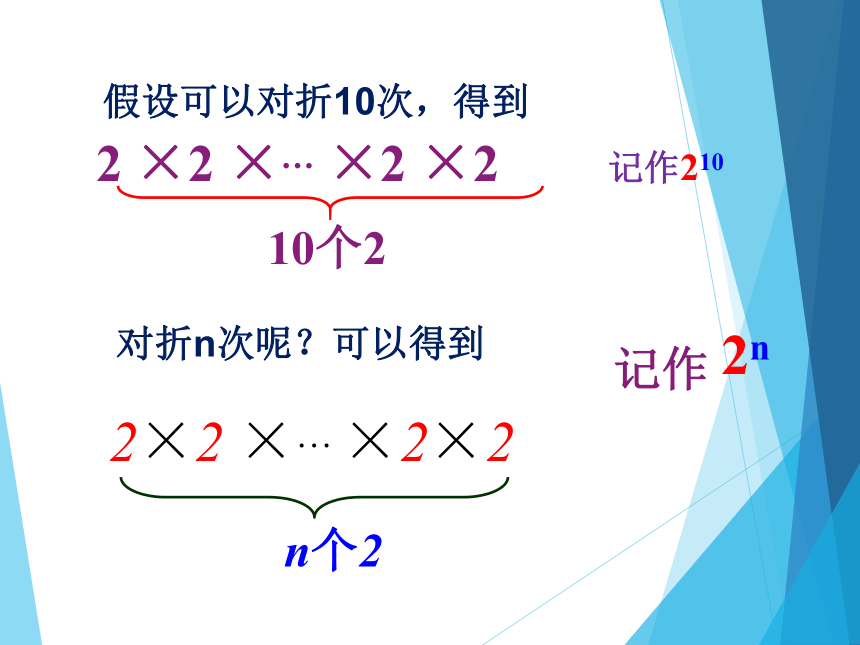
2 ×2 ×… ×2 ×2
10个2
记作
2n
假设可以对折10次,得到
记作210
对折n次呢?可以得到
2×2 ×… ×2×2
n个2
an
底数
指数
幂
n个a
an=
求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂,在an中,a叫作底数,n叫作指数,当 an 看作一个结果时,也可以读作 a 的 n次幂.
a×a ×… ×a ×a
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.
乘方也和加、减、乘、除一样是
一种运算,幂是乘方运算的结果,
下面是五种运算及运算结果的一览表。
运算
加
减
乘
除
乘方
运算
结果
幂
和
差
积
商
说出下列各式的底数、指数、及其意义
(-
)
3
)
(
2
口答练习一
把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3) ×(-1.3) ×(-1.3) ×(-1.3)
4. m·m ·m ·… ·m
2a个
例1 :计算
(1)(-4)3
(2)(-2)4=
当指数是 时,负数的幂是负数
奇数
当指数是 时负数的幂是正数
偶数
从例1,你发现负数的幂的正负有什么规律?
-64
16
(3)
=(-4)×( -4)×( -4)=
(-2) ×(-2) ×(-2) ×(-2)=
×
×
27
8
-
=
计算:
结论:
(-1)的偶数次幂为_1__
(-1)的奇数次幂为__-1_
1的任何次幂为__1__
0的正整数次幂为___0_
=1
=1
=1
=-1
=0
=0
-24和(-2)4的区别.
讨 论
-24表示有负的4个2相乘(或表示2的4次方的相反数),于是结果的符号应是负号;而(-2)4表示有4个-2相乘,当然有偶数个(4个)负因数,结果的符号应是正号.
解: -24=-1×24=-16
(-2)4=16
练习二
1 判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( ) ④
对
错
错
错
练习三
=1
=8×8×8=512
=(-5)×(-5)×(-5)=-125
=0.1×0.1×0.1=0.001
=(-10)×(-10)×(-10)×(-10)=10000
×
×
×
=
×
=
=
×
×
(1)正数的任何次幂是正数;
乘方运算的符号规律
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.
(3) 0的任何正整数次幂等于零;
1的任何次幂等于1.
(2)负数的偶次幂是正数;
负数的奇次幂是负数;
(4) (-1)的偶数次幂为_1__
(-1)的奇数次幂为__-1
本节课你学到了什么
1.有理数的乘方的意义和相关概念。
3.乘方的有关运算。
2.幂的底数是分数或负数时,底数应该添上括号.
1.5 有理数的乘方
第一章 有理数
国王和大臣
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。第1格放2粒,第2格放4粒米,第3格放8粒米,然后是16粒、32粒、64粒……一直到第64格。”“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!” 你认为国王的国库里有这么多米吗
复习提问:
1.5.1 有理数的乘方
几个不是0的有理数相乘,积的符号是由什么确定的?
积的符号是由负因数的个数确定的,
当负因数的个数为偶数时,积的符号为正;
当负因数的个数为奇数时,积的符号为负.
问题情境:将一张纸对折一次,会得到多少层纸?对折二次,三次,四次呢?对折n次呢?你能发现层数和对折的次数有什么关系吗?
将一张纸对折一次时得到 2 层纸
对折二次时得到 2×2 层纸
对折四次时得到 2×2×2×2 层纸
对折三次时得到 2×2×2 层纸
…,
记作22
记作23
记作24
2 ×2 ×… ×2 ×2
10个2
记作
2n
假设可以对折10次,得到
记作210
对折n次呢?可以得到
2×2 ×… ×2×2
n个2
an
底数
指数
幂
n个a
an=
求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂,在an中,a叫作底数,n叫作指数,当 an 看作一个结果时,也可以读作 a 的 n次幂.
a×a ×… ×a ×a
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.
乘方也和加、减、乘、除一样是
一种运算,幂是乘方运算的结果,
下面是五种运算及运算结果的一览表。
运算
加
减
乘
除
乘方
运算
结果
幂
和
差
积
商
说出下列各式的底数、指数、及其意义
(-
)
3
)
(
2
口答练习一
把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3) ×(-1.3) ×(-1.3) ×(-1.3)
4. m·m ·m ·… ·m
2a个
例1 :计算
(1)(-4)3
(2)(-2)4=
当指数是 时,负数的幂是负数
奇数
当指数是 时负数的幂是正数
偶数
从例1,你发现负数的幂的正负有什么规律?
-64
16
(3)
=(-4)×( -4)×( -4)=
(-2) ×(-2) ×(-2) ×(-2)=
×
×
27
8
-
=
计算:
结论:
(-1)的偶数次幂为_1__
(-1)的奇数次幂为__-1_
1的任何次幂为__1__
0的正整数次幂为___0_
=1
=1
=1
=-1
=0
=0
-24和(-2)4的区别.
讨 论
-24表示有负的4个2相乘(或表示2的4次方的相反数),于是结果的符号应是负号;而(-2)4表示有4个-2相乘,当然有偶数个(4个)负因数,结果的符号应是正号.
解: -24=-1×24=-16
(-2)4=16
练习二
1 判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( ) ④
对
错
错
错
练习三
=1
=8×8×8=512
=(-5)×(-5)×(-5)=-125
=0.1×0.1×0.1=0.001
=(-10)×(-10)×(-10)×(-10)=10000
×
×
×
=
×
=
=
×
×
(1)正数的任何次幂是正数;
乘方运算的符号规律
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.
(3) 0的任何正整数次幂等于零;
1的任何次幂等于1.
(2)负数的偶次幂是正数;
负数的奇次幂是负数;
(4) (-1)的偶数次幂为_1__
(-1)的奇数次幂为__-1
本节课你学到了什么
1.有理数的乘方的意义和相关概念。
3.乘方的有关运算。
2.幂的底数是分数或负数时,底数应该添上括号.
