四川省广安市2012-2013学年高二下学期期末考试数学(文)试题
文档属性
| 名称 | 四川省广安市2012-2013学年高二下学期期末考试数学(文)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-15 00:00:00 | ||
图片预览


文档简介
广安市2013年高二期末试题
数学(文科)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
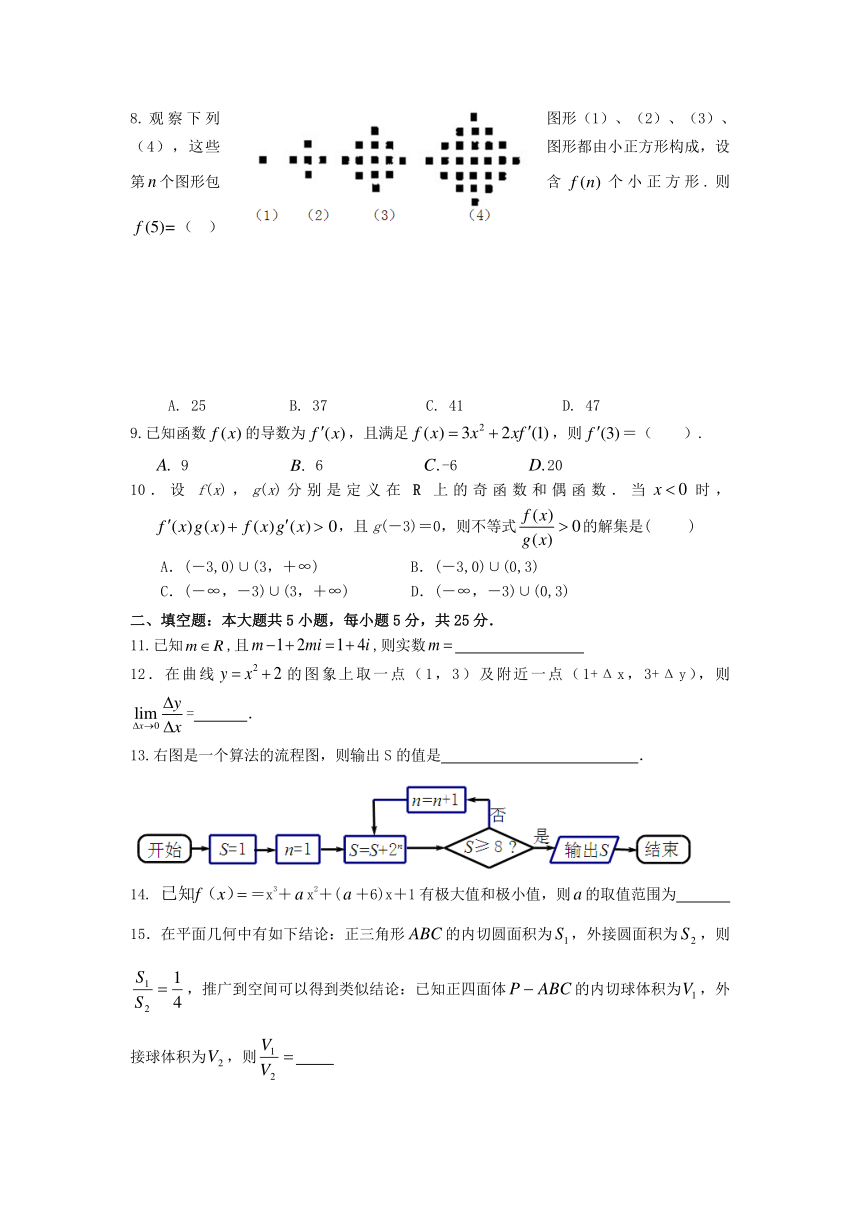
1.复数在复平面内所表示的点在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.曲线在点处的切线的斜率为 ( )
A.1 B.-1 C. D.
3.在曲线上切线倾斜角为的点是 ( )
A.(0,0) B.(2,4) C. D.
4.设复数z的共轭复数,若则= ( )
A. 5 B 25 C 625 D 不确定
5. 观察:32 – 1 =8, 52 – 1 = 24,72 – 1 = 48,92 – 1 =80,…,则第n个等式是 ( )
A. B.
C. D.
6.函数的定义域为开区间,导函数 在 内的图象如图所示,则函数在开区间内有极小值点 ( )
A.1个 B. 2个 C.3个 D.4个
7. 函数在区间上是 ( )
A.单调增函数 B .在上是增函数,在上是减函数
C. 单调减函数 D. 在上是减函数,在是增函数
8.观察下列图形(1)、(2)、(3)、(4),这些图形都由小正方形构成,设第个图形包含个小正方形.则( )
A. 25 B. 37 C. 41 D. 47
9.已知函数的导数为,且满足,则=( ).
9 6 -6 20
10.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当时,,且g(-3)=0,则不等式的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
二、填空题:本大题共5小题,每小题5分,共25分.
11.已知,且,则实数
12.在曲线的图象上取一点(1,3)及附近一点(1+Δx,3+Δy),则= .
13.右图是一个算法的流程图,则输出S的值是 .
14. =x3+x2+(+6)x+1有极大值和极小值,则的取值范围为
15.在平面几何中有如下结论:正三角形的内切圆面积为,外接圆面积为,则,推广到空间可以得到类似结论:已知正四面体的内切球体积为,外接球体积为,则
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)已知函数
(Ⅰ)求;
(Ⅱ)求的极大值.
18.(本小题满分12分)已知函数的图像经过点,曲线在点处的切线恰好与直线垂直.
(Ⅰ)求实数的值;
(Ⅱ)若函数在区间上单调递减,求的取值范围.
19.(本小题满分12分)
用反证法证明:如果,那么.
20.(本题13分)已知在区间[0,1]上是减函数,在区间上是增函数,又.
(1) 求的解析式;
(2) 若在区间上恒有≤5x成立,求m的取值范围。
21.(本小题满分14分)
已知函数,。
(Ⅰ)当时,求的单调区间;
(Ⅱ)若函数在上是减函数,求实数的取值范围;
(Ⅲ)令,是否存在负实数,当(e是自然对数的底数)时,函数的最小值是2,若存在,求出的值;若不存在,说明理由。
广安市2013年高二期末试题
数学(文科)答案
一、选择题:
1—5 C B D A C 6—10 A D C B A
二、填空题:
11、2, 12、2, 13、15 , 14、, 15、
三、解答题:
16. (本题12分)解. (1),,-------4分
(2),
列表如下:
0
0
极大值
极小值
可知,当x=-1时,f(x)取得极大值f(-1)=2, ----------------12分
17.解:(1)
解得
-----------------6分
(2)由题知,,解得
即 ----------------12分
18 . 解:(Ⅰ)的图象经过点 ∴---1分
∵,∴ -------------2分
由已知条件知 即 -------------4分
∴解 得: -------------6分
(Ⅱ)由(Ⅰ)知,
令,则 --------------8分
∵函数在区间上单调递减 ∴
,即 ---------------12分
19(本题12分)
证明二.假设,则,或. …………2分
若,显然,这与已知矛盾; . …………4分
若,则,这与已知矛盾;. ……10分
综上,假设不成立,故原命题成立。 . …………12分
20. (本题13分)解:(Ⅰ),
由已知, -----------------2分
即解得 -----------------4分
,,, -----5分
. ----------------7分
(Ⅱ)令,即,,
. -----------------10分
又在区间上恒成立,
. -----------------13分
21、(本题14分)解:(Ⅰ)当a=1时,由
但函数的定义域为
所以当,当
所以函数的单调递减区间为,
单调递增区间为 ………………4分
(Ⅱ)若函数在上是减函数,
则 在上恒成立,
因为x>0, 令 ,
有 得 得 ……………………8分
(III)假设存在负实数,使,即()有最小值2,
……………9分
(1) 当,即时,在上单调递减,在上单调递增
,,满足条件. ………11分
(2) 当,即时,,在上单调递减,
此时,(舍去),即无最小值.…13分
综上,存在负实数,使得当时,有最小值2. ……14分
数学(文科)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数在复平面内所表示的点在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.曲线在点处的切线的斜率为 ( )
A.1 B.-1 C. D.
3.在曲线上切线倾斜角为的点是 ( )
A.(0,0) B.(2,4) C. D.
4.设复数z的共轭复数,若则= ( )
A. 5 B 25 C 625 D 不确定
5. 观察:32 – 1 =8, 52 – 1 = 24,72 – 1 = 48,92 – 1 =80,…,则第n个等式是 ( )
A. B.
C. D.
6.函数的定义域为开区间,导函数 在 内的图象如图所示,则函数在开区间内有极小值点 ( )
A.1个 B. 2个 C.3个 D.4个
7. 函数在区间上是 ( )
A.单调增函数 B .在上是增函数,在上是减函数
C. 单调减函数 D. 在上是减函数,在是增函数
8.观察下列图形(1)、(2)、(3)、(4),这些图形都由小正方形构成,设第个图形包含个小正方形.则( )
A. 25 B. 37 C. 41 D. 47
9.已知函数的导数为,且满足,则=( ).
9 6 -6 20
10.设f(x),g(x)分别是定义在R上的奇函数和偶函数.当时,,且g(-3)=0,则不等式的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3)
二、填空题:本大题共5小题,每小题5分,共25分.
11.已知,且,则实数
12.在曲线的图象上取一点(1,3)及附近一点(1+Δx,3+Δy),则= .
13.右图是一个算法的流程图,则输出S的值是 .
14. =x3+x2+(+6)x+1有极大值和极小值,则的取值范围为
15.在平面几何中有如下结论:正三角形的内切圆面积为,外接圆面积为,则,推广到空间可以得到类似结论:已知正四面体的内切球体积为,外接球体积为,则
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)已知函数
(Ⅰ)求;
(Ⅱ)求的极大值.
18.(本小题满分12分)已知函数的图像经过点,曲线在点处的切线恰好与直线垂直.
(Ⅰ)求实数的值;
(Ⅱ)若函数在区间上单调递减,求的取值范围.
19.(本小题满分12分)
用反证法证明:如果,那么.
20.(本题13分)已知在区间[0,1]上是减函数,在区间上是增函数,又.
(1) 求的解析式;
(2) 若在区间上恒有≤5x成立,求m的取值范围。
21.(本小题满分14分)
已知函数,。
(Ⅰ)当时,求的单调区间;
(Ⅱ)若函数在上是减函数,求实数的取值范围;
(Ⅲ)令,是否存在负实数,当(e是自然对数的底数)时,函数的最小值是2,若存在,求出的值;若不存在,说明理由。
广安市2013年高二期末试题
数学(文科)答案
一、选择题:
1—5 C B D A C 6—10 A D C B A
二、填空题:
11、2, 12、2, 13、15 , 14、, 15、
三、解答题:
16. (本题12分)解. (1),,-------4分
(2),
列表如下:
0
0
极大值
极小值
可知,当x=-1时,f(x)取得极大值f(-1)=2, ----------------12分
17.解:(1)
解得
-----------------6分
(2)由题知,,解得
即 ----------------12分
18 . 解:(Ⅰ)的图象经过点 ∴---1分
∵,∴ -------------2分
由已知条件知 即 -------------4分
∴解 得: -------------6分
(Ⅱ)由(Ⅰ)知,
令,则 --------------8分
∵函数在区间上单调递减 ∴
,即 ---------------12分
19(本题12分)
证明二.假设,则,或. …………2分
若,显然,这与已知矛盾; . …………4分
若,则,这与已知矛盾;. ……10分
综上,假设不成立,故原命题成立。 . …………12分
20. (本题13分)解:(Ⅰ),
由已知, -----------------2分
即解得 -----------------4分
,,, -----5分
. ----------------7分
(Ⅱ)令,即,,
. -----------------10分
又在区间上恒成立,
. -----------------13分
21、(本题14分)解:(Ⅰ)当a=1时,由
但函数的定义域为
所以当,当
所以函数的单调递减区间为,
单调递增区间为 ………………4分
(Ⅱ)若函数在上是减函数,
则 在上恒成立,
因为x>0, 令 ,
有 得 得 ……………………8分
(III)假设存在负实数,使,即()有最小值2,
……………9分
(1) 当,即时,在上单调递减,在上单调递增
,,满足条件. ………11分
(2) 当,即时,,在上单调递减,
此时,(舍去),即无最小值.…13分
综上,存在负实数,使得当时,有最小值2. ……14分
同课章节目录
