23.1图形的旋转(1) 课件(共29张PPT)
文档属性
| 名称 | 23.1图形的旋转(1) 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 09:53:01 | ||
图片预览




文档简介
(共29张PPT)
人教版 九年级上册
23.1图形的旋转(1)
学习目标:
1.通过观察具体实例学习旋转概念,会画一个图形 作旋转后所得的图形;
2.探究旋转的性质,并在观察、猜想、验证、归纳、 概括的探究过程中,发展合情推理能力,进一步 体会图形运动中的变和不变.
·学习重点: 旋转的性质.
课件说明
本课是在学生已经学移、轴对称的有关知识的 基础上,进一步研究旋转的概念和旋转的性质,以及 应用旋转性质画一个图形作旋转后所得的图形.
课件说明
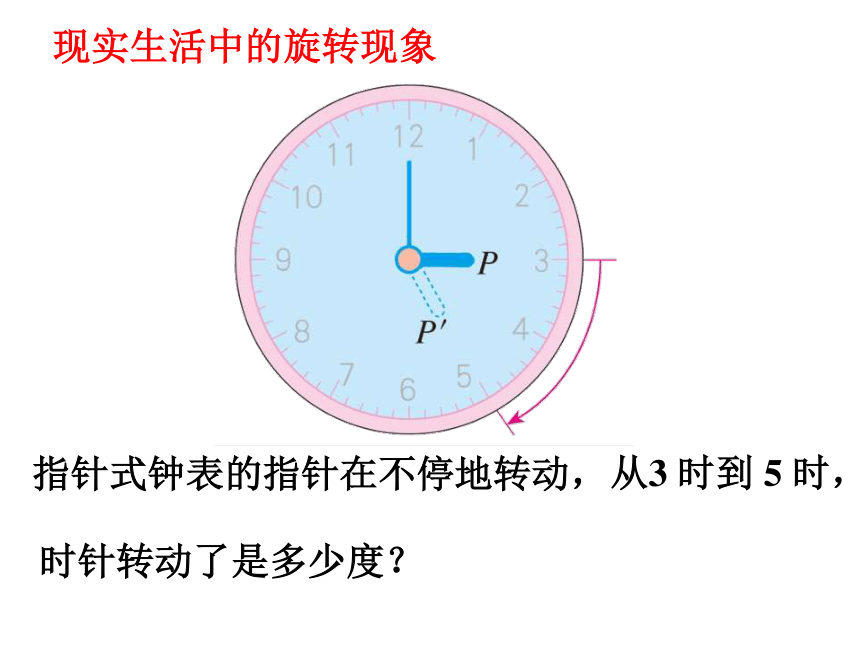
指针式钟表的指针在不停地转动,
时针转动了是多少度?
从3 时到 5 时,
现实生活中的旋转现象
风车风轮的每个叶片在风的吹动下转动到
新的位置.
现实生活中的旋转现象
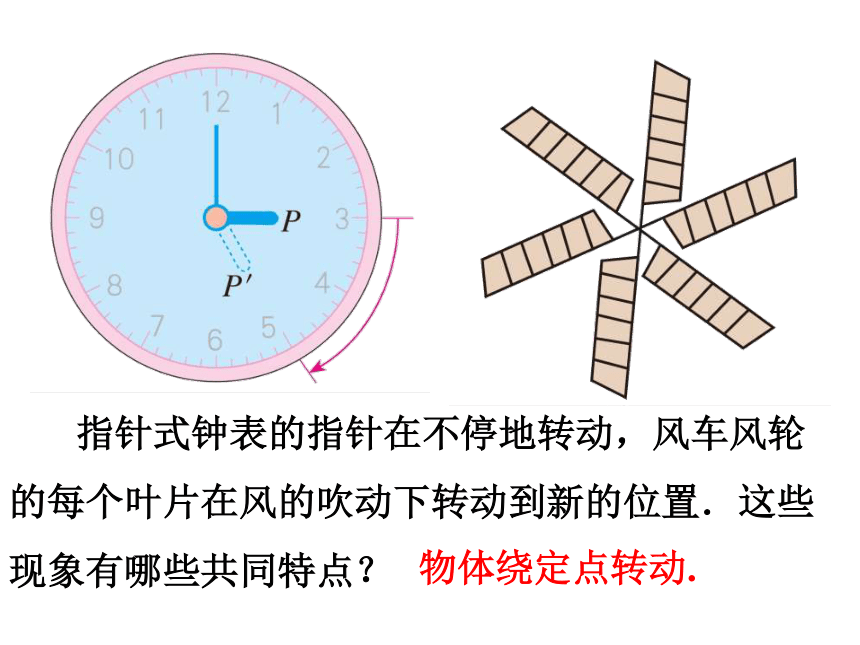
指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?
物体绕定点转动.
O
P′
P
120°
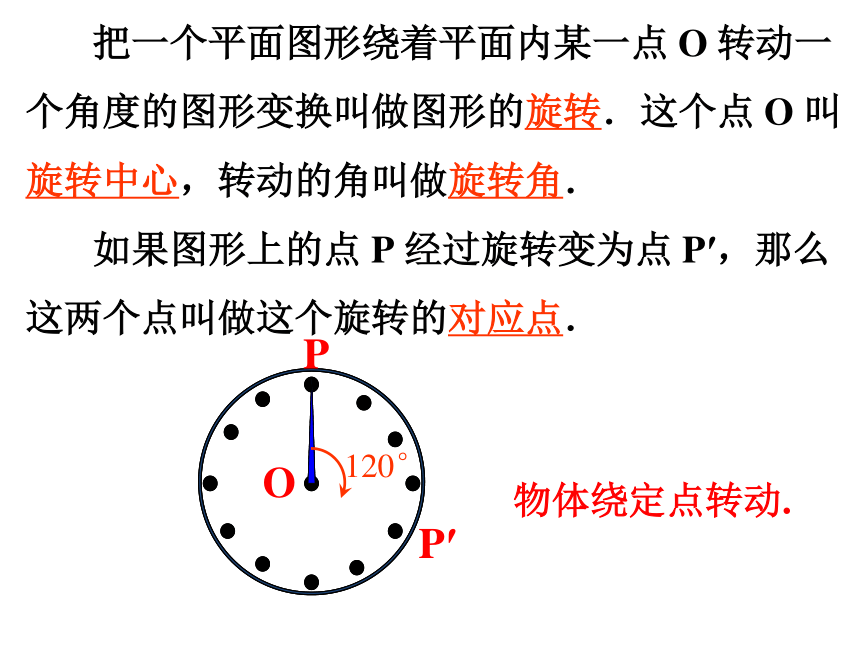
把一个平面图形绕着平面内某一点 O 转动一个角度的图形变换叫做图形的旋转.这个点 O 叫旋转中心,转动的角叫做旋转角. 如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
物体绕定点转动.
1.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转的旋转角是多少度?从上午 9 时到上午 10 时呢?
上午 6 时到上午 9 时,时针旋转的旋转角是60度;
上午 9 时到上午 10 时,时针旋转的旋转角是30度.
认识新知
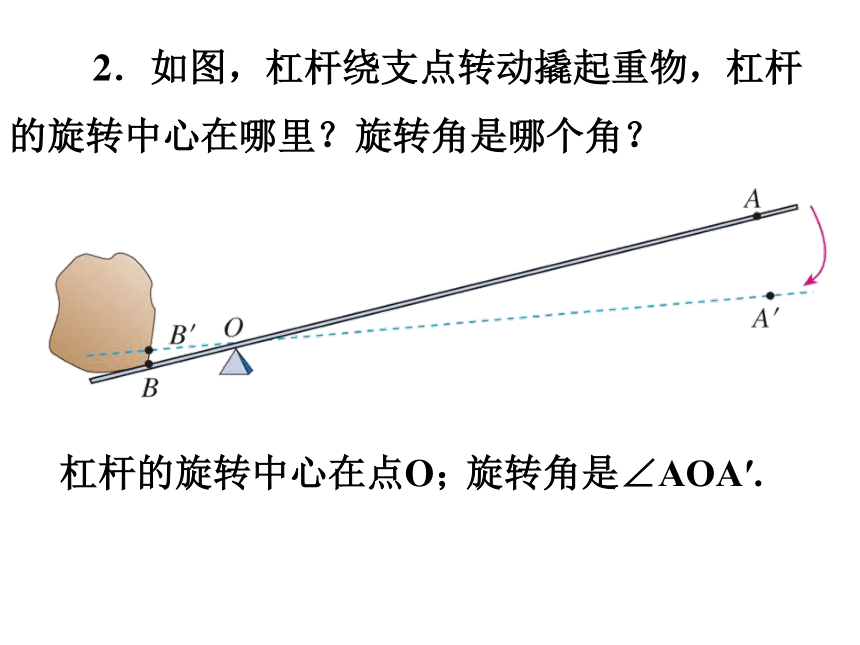
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
杠杆的旋转中心在点O;
旋转角是∠AOA′.
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O 作为旋转中心,硬纸板下面放一张白纸,先在纸上描出 这个挖掉的三角形图案(△ABC),然后围绕旋转中心 转动硬纸板,再描出这个挖掉的三角形(△A ′ B ′ C ′), 移开硬纸板.请同学们思考以下问题:
'
'
'
探究旋转的性质
(1)△A′B′C′ 可以
看作由△ABC以点O
为旋转中心,沿顺时针方向,旋转一定的角度得到的.
(1)△A′B′C′ 可以看作 △ABC 经过怎样的运动得到的?
A
B
C
A′
B′
C′
O
(2)线段 OA 和 OA' 有什么关系?∠AOA'和∠BOB'有什么关系?
(3)你还能发现哪些有类似关系的线段和角?
OA=
OA'
∠AOA'=
∠BOB'
OB=
OB'
OC=
OC'
∠AOA'=
∠COC'
∠BOB'=
∠COC'
A
B
C
A′
B′
C′
O
(4)△ABC和△A′B′C′ 的形状和大小有什么关系?
△ABC≌△A′B′C′
A
B
C
A′
B′
C′
O
1. 对应点到旋转中心的距离相等.
2. 对应点与旋转中心所连线段的
夹角等于旋转角.
3.旋转前、后的图形全等.
(5)把以上发现,用自己的语言归纳概括一下.
旋转的性质
A
B
C
A′
B′
C′
O
A
B
O
例1下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出△OAB 旋转后的图形 △OA ′ B ′吗?
A'
B'
例题解析
(1)如何画出旋转后的图形?
(2)如何确定旋转后的对应点的位置?
归纳
1.确定旋转中心;
2.确定旋转方向;
3.确定旋转角.
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于
旋转角.
例2 如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能画出旋转后的图形吗?试一试你有几种方法?
A
B
C
E
D
例题解析
延长CB,在CB的延长线上截取BF,使BF=DE,连接AF,
方法1:
F
则△ABF为所求图形.
A
B
C
E
D
方法2:
F
A
B
C
E
D
过点A作AF⊥AE,交CB的延长线于F,
则△ABF为所求图形.
1.下列图形中既是轴对称图形,又是旋转对称图形
的是( ).
A. (1)(2)(3)(4) B. (1)(2)(3)
C. (2)(3)(4) D. (1)(3)(4)
D
2.如图,将△AOB绕点O按逆时针方向旋转45°
得到△A ′ OB ′.若∠AOB=21°,则∠BOB ′
的度数是( ).
A. 21° B.24° C.45° D.66°
A
O
B
A ′
B ′
C
3.如图,将△ OAB绕点O逆时针旋转70°到
△OCD的位置若∠AOB=40°,则∠AOD
等于( ).
A.45° B.40° C. 35° D. 30°
A
O
B
C
D
D
4.如图,把正△ ABC 绕其中心O旋转一定角度后
与自身重合,则这个旋转角度至少为( ).
A.360° B.240° C.120° D.60°
A
B
C
O
C
5.如图,两块相同的直角三角板完全重合在一起,
∠A=30°,AC=10.把上面一块绕直角顶点B逆
时针旋转到△ABC的位置,点C在AC上,
则 BC ′ = ,CC ′ = .
A
C
B
A′
C′
5
5
6.将如图 的“十字星”图形绕其中心点O旋转,
当至少旋转 度后,所得图形与原图形重合.
O
90
7.如图,将直角三角形ABC绕直角顶点C顺时针
旋转90°,得到△A1B1C,连接AA1.若∠1=20°,
则∠CA1B1= .
A
C
B
A1
B1
1
25°
对比平移、轴对称,旋转的性质,它们有哪些相同点和不同点?
小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
23.1图形的旋转(1)
学习目标:
1.通过观察具体实例学习旋转概念,会画一个图形 作旋转后所得的图形;
2.探究旋转的性质,并在观察、猜想、验证、归纳、 概括的探究过程中,发展合情推理能力,进一步 体会图形运动中的变和不变.
·学习重点: 旋转的性质.
课件说明
本课是在学生已经学移、轴对称的有关知识的 基础上,进一步研究旋转的概念和旋转的性质,以及 应用旋转性质画一个图形作旋转后所得的图形.
课件说明
指针式钟表的指针在不停地转动,
时针转动了是多少度?
从3 时到 5 时,
现实生活中的旋转现象
风车风轮的每个叶片在风的吹动下转动到
新的位置.
现实生活中的旋转现象
指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?
物体绕定点转动.
O
P′
P
120°
把一个平面图形绕着平面内某一点 O 转动一个角度的图形变换叫做图形的旋转.这个点 O 叫旋转中心,转动的角叫做旋转角. 如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
物体绕定点转动.
1.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转的旋转角是多少度?从上午 9 时到上午 10 时呢?
上午 6 时到上午 9 时,时针旋转的旋转角是60度;
上午 9 时到上午 10 时,时针旋转的旋转角是30度.
认识新知
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
杠杆的旋转中心在点O;
旋转角是∠AOA′.
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O 作为旋转中心,硬纸板下面放一张白纸,先在纸上描出 这个挖掉的三角形图案(△ABC),然后围绕旋转中心 转动硬纸板,再描出这个挖掉的三角形(△A ′ B ′ C ′), 移开硬纸板.请同学们思考以下问题:
'
'
'
探究旋转的性质
(1)△A′B′C′ 可以
看作由△ABC以点O
为旋转中心,沿顺时针方向,旋转一定的角度得到的.
(1)△A′B′C′ 可以看作 △ABC 经过怎样的运动得到的?
A
B
C
A′
B′
C′
O
(2)线段 OA 和 OA' 有什么关系?∠AOA'和∠BOB'有什么关系?
(3)你还能发现哪些有类似关系的线段和角?
OA=
OA'
∠AOA'=
∠BOB'
OB=
OB'
OC=
OC'
∠AOA'=
∠COC'
∠BOB'=
∠COC'
A
B
C
A′
B′
C′
O
(4)△ABC和△A′B′C′ 的形状和大小有什么关系?
△ABC≌△A′B′C′
A
B
C
A′
B′
C′
O
1. 对应点到旋转中心的距离相等.
2. 对应点与旋转中心所连线段的
夹角等于旋转角.
3.旋转前、后的图形全等.
(5)把以上发现,用自己的语言归纳概括一下.
旋转的性质
A
B
C
A′
B′
C′
O
A
B
O
例1下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出△OAB 旋转后的图形 △OA ′ B ′吗?
A'
B'
例题解析
(1)如何画出旋转后的图形?
(2)如何确定旋转后的对应点的位置?
归纳
1.确定旋转中心;
2.确定旋转方向;
3.确定旋转角.
1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连线段的夹角等于
旋转角.
例2 如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,你能画出旋转后的图形吗?试一试你有几种方法?
A
B
C
E
D
例题解析
延长CB,在CB的延长线上截取BF,使BF=DE,连接AF,
方法1:
F
则△ABF为所求图形.
A
B
C
E
D
方法2:
F
A
B
C
E
D
过点A作AF⊥AE,交CB的延长线于F,
则△ABF为所求图形.
1.下列图形中既是轴对称图形,又是旋转对称图形
的是( ).
A. (1)(2)(3)(4) B. (1)(2)(3)
C. (2)(3)(4) D. (1)(3)(4)
D
2.如图,将△AOB绕点O按逆时针方向旋转45°
得到△A ′ OB ′.若∠AOB=21°,则∠BOB ′
的度数是( ).
A. 21° B.24° C.45° D.66°
A
O
B
A ′
B ′
C
3.如图,将△ OAB绕点O逆时针旋转70°到
△OCD的位置若∠AOB=40°,则∠AOD
等于( ).
A.45° B.40° C. 35° D. 30°
A
O
B
C
D
D
4.如图,把正△ ABC 绕其中心O旋转一定角度后
与自身重合,则这个旋转角度至少为( ).
A.360° B.240° C.120° D.60°
A
B
C
O
C
5.如图,两块相同的直角三角板完全重合在一起,
∠A=30°,AC=10.把上面一块绕直角顶点B逆
时针旋转到△ABC的位置,点C在AC上,
则 BC ′ = ,CC ′ = .
A
C
B
A′
C′
5
5
6.将如图 的“十字星”图形绕其中心点O旋转,
当至少旋转 度后,所得图形与原图形重合.
O
90
7.如图,将直角三角形ABC绕直角顶点C顺时针
旋转90°,得到△A1B1C,连接AA1.若∠1=20°,
则∠CA1B1= .
A
C
B
A1
B1
1
25°
对比平移、轴对称,旋转的性质,它们有哪些相同点和不同点?
小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
