23.1图形的旋转(2) 课件(共30张PPT)
文档属性
| 名称 | 23.1图形的旋转(2) 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 09:53:23 | ||
图片预览




文档简介
(共30张PPT)
人教版 九年级上册
23.1图形的旋转(2)
学习目标: 1.理解选择不同的旋转中心、不同的旋转角度对某 一图案作旋转,会出现不同的效果,掌握根据需 要用旋转的知识设计出美丽的图案; 2.复习图形旋转的基本性质,着重强调旋转中心和 旋转角,然后应用已学的知识作图,设计出美丽 的图案.
学习重点: 根据需要设计美丽图案.
课件说明
学生在上节课已经学习了旋转概念、旋转的性质.这 为本节学习奠定了一定的基础.这节课就来具体应用 一下.选择不同的旋转中心,不同的旋转角度,旋转 同一个图形,观察出现的不同效果.
选择不同的旋转中心或不同的旋转角,画出一个图形旋转后的图形.
课件说明
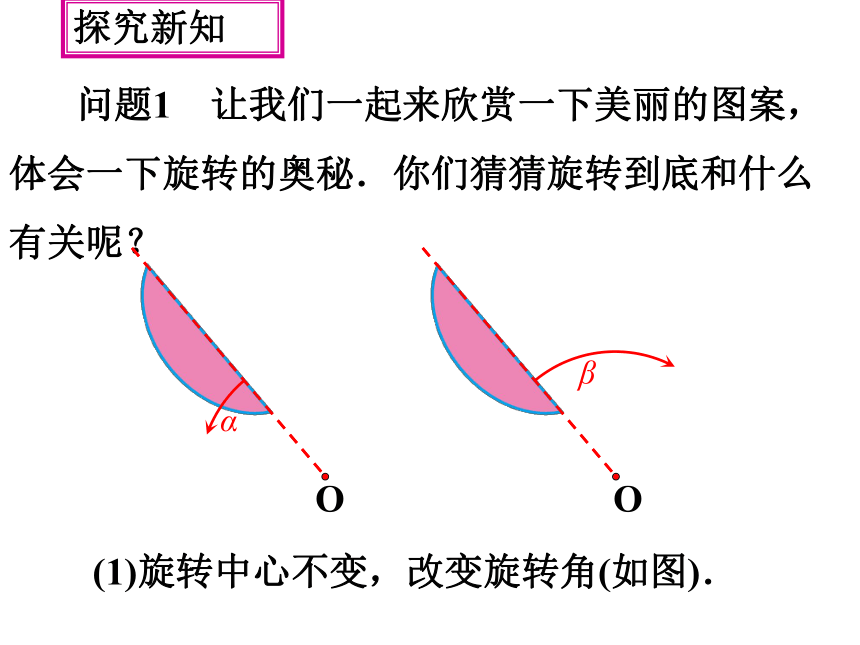
(1)旋转中心不变,改变旋转角(如图).
问题1 让我们一起来欣赏一下美丽的图案,体会一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
O
O
β
α
探究新知
O1
α
O2
α
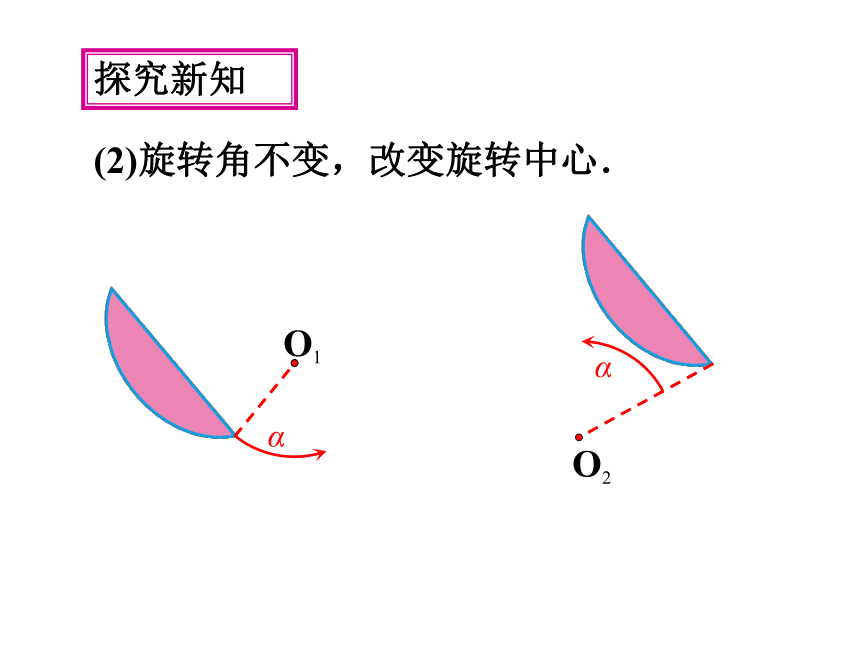
(2)旋转角不变,改变旋转中心.
探究新知
(3)美丽的图案是这样形成的.
探究新知
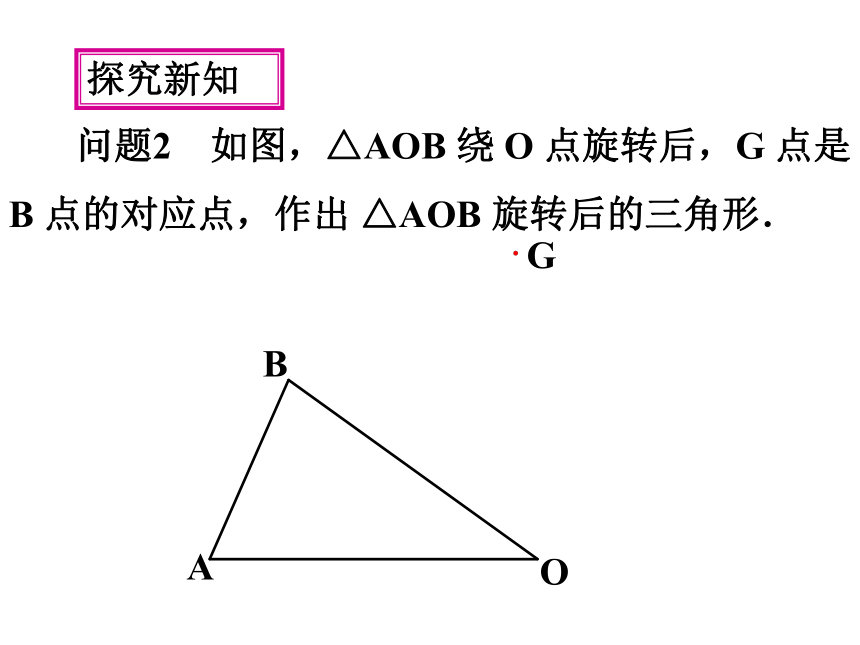
问题2 如图,△AOB 绕 O 点旋转后,G 点是 B 点的对应点,作出 △AOB 旋转后的三角形.
G
O
A
B
探究新知
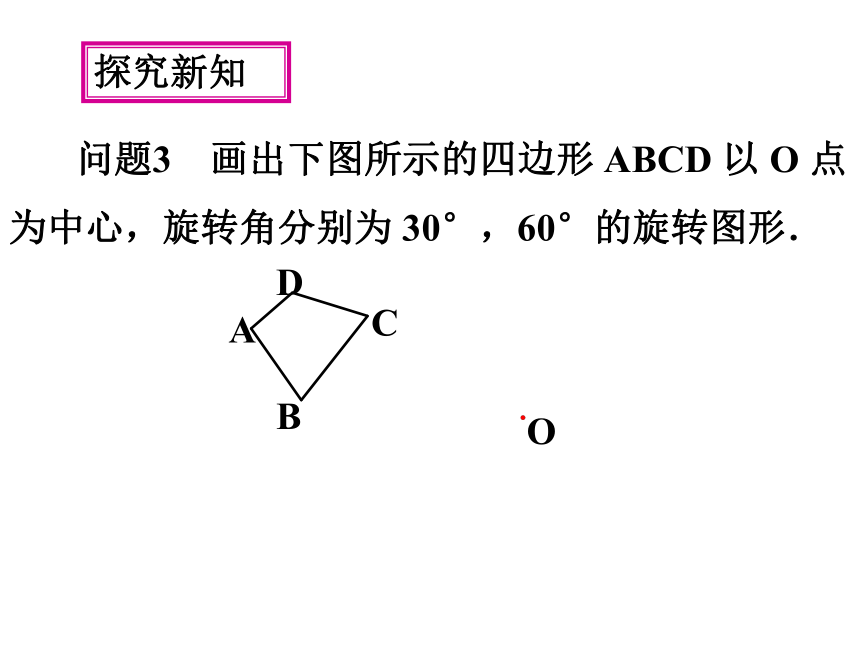
问题3 画出下图所示的四边形 ABCD 以 O 点为中心,旋转角分别为 30°,60°的旋转图形.
O
A
B
C
D
探究新知
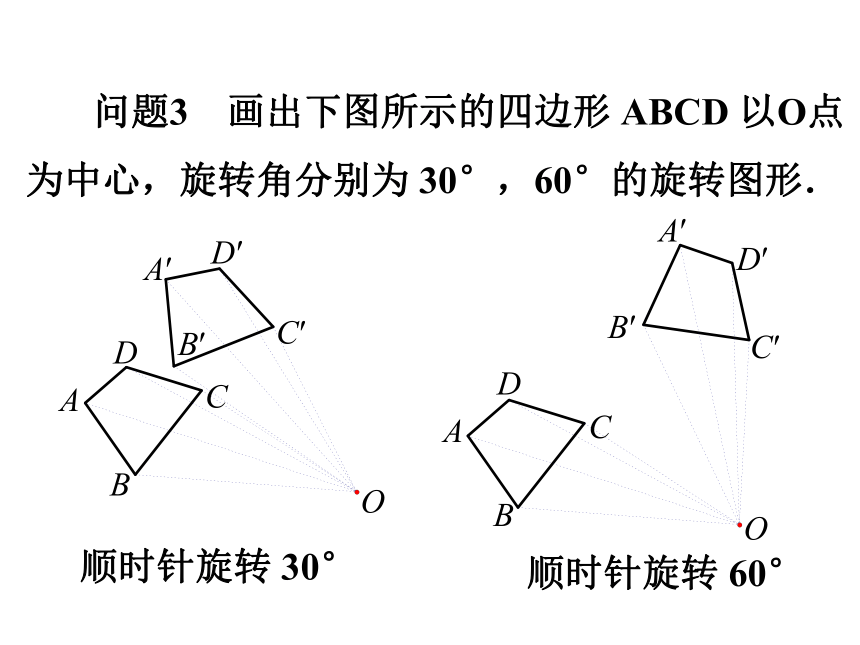
问题3 画出下图所示的四边形 ABCD 以O点为中心,旋转角分别为 30°,60°的旋转图形.
A
B
C
D
O
A′
B′
C′
D′
O
A
B
C
D
A′
D′
C′
B′
顺时针旋转 60°
顺时针旋转 30°
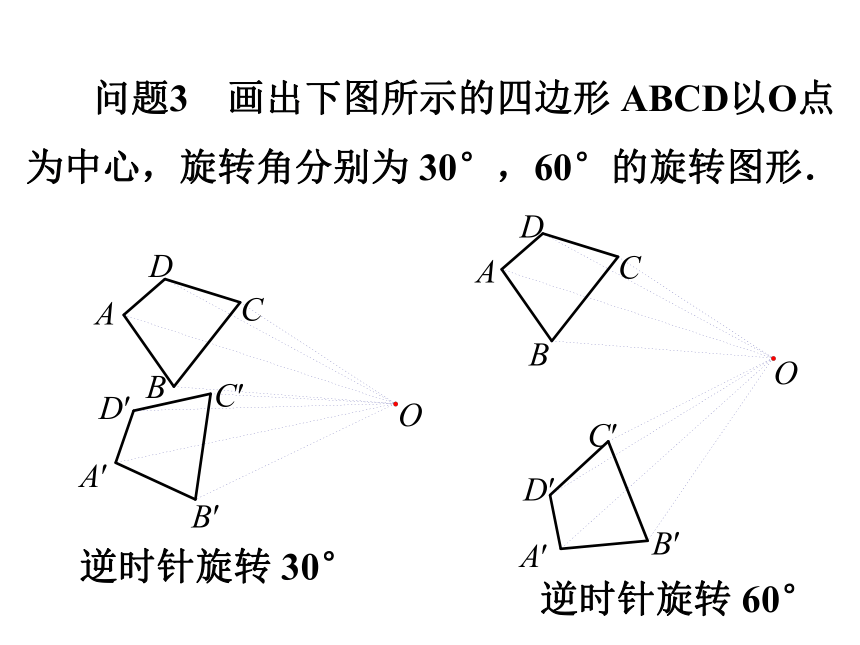
问题3 画出下图所示的四边形 ABCD以O点为中心,旋转角分别为 30°,60°的旋转图形.
O
A
B
C
D
B′
A′
D′
C′
O
A
B
C
D
B′
A′
D′
C′
逆时针旋转 60°
逆时针旋转 30°
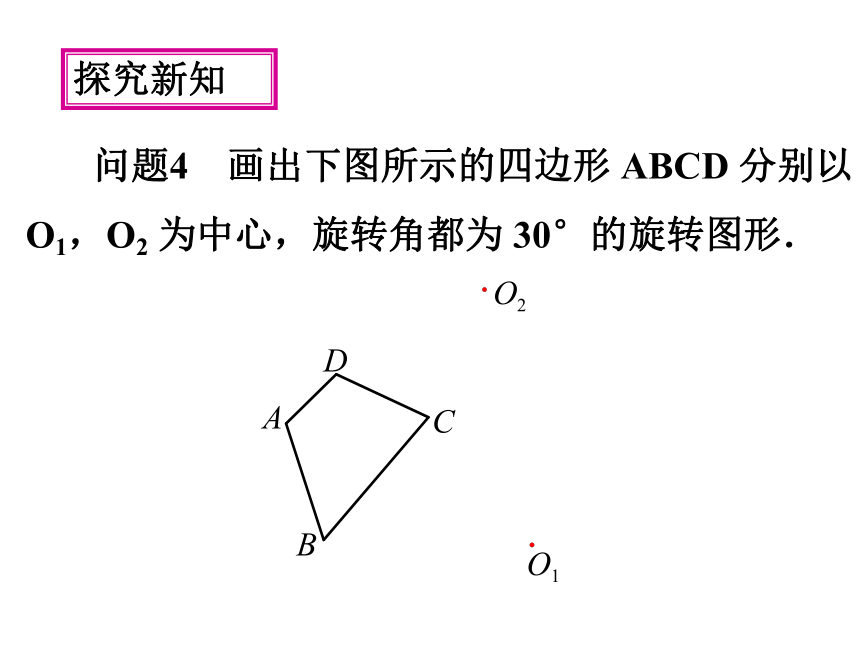
问题4 画出下图所示的四边形 ABCD 分别以 O1,O2 为中心,旋转角都为 30°的旋转图形.
探究新知
A
B
C
D
O1
O2
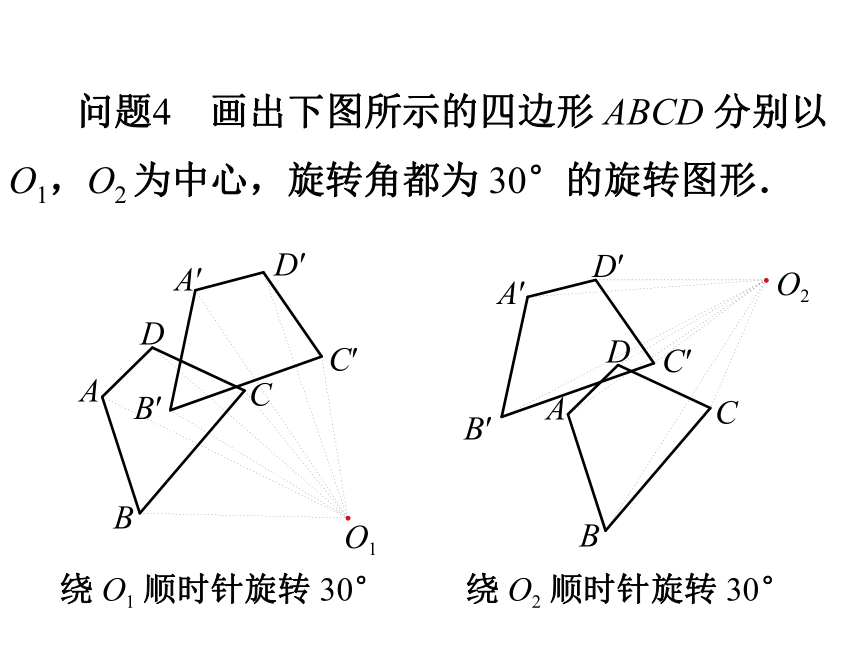
问题4 画出下图所示的四边形 ABCD 分别以 O1,O2 为中心,旋转角都为 30°的旋转图形.
A
B
C
D
O1
A′
B′
C′
D′
A
B
C
D
O2
A′
B′
D′
C′
绕 O1 顺时针旋转 30°
绕 O2 顺时针旋转 30°
问题4 画出下图所示的四边形 ABCD 分别以 O1, O2 为中心,旋转角都为 30°的旋转图形.
A
B
C
D
O1
A′
B′
C′
D′
A
B
C
D
O2
D′
A′
B′
C′
绕 O1 逆时针旋转 30°
绕 O2 逆时针旋转 30°
O
例1 如下图是某一种花的花瓣和中心,现以 O 为旋转中心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.
例题解析
例2 如图,如果这种花的一片花瓣,绕旋转中心点O′旋转,请同学画出旋转后的图形.
O′
例题解析
把一个三角形进行旋转:
(1)选择不同的旋转中心,不同的旋转角,看看旋 转的效果;
巩固练习
(2)改变三角形的形状,看看旋转的效果.
3.巩固练习
归纳小结
(1)本节课学了哪些主要内容? (2)怎样画一个图形关于一个点的旋转图形?
1.下列运动形式属于旋转的是( ).
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
C
巩固新知
2.点A(4,2)经过某种图形变换后得到点
B(-2,4),这种图形变换可以是( )
A.关于x轴对称
B.关于y轴对称
C.绕原点逆时针旋转90°
D.绕原点顺时针旋转90°
C
3.如图,线段AB 绕着点O旋转一定的角度
得线段A'B'.下列结论错误的是( ).
A.AB=A'B' B. ∠AOA'=∠BOB'
C.OB=OB' D. ∠AOB'=100°
D
A
B
O
A'
B'
4.如图 ,在△ABC中,∠BAC=30°,AB=8,
AC=6.将 △ ABC绕点A逆时针旋转60°得
到△AB1C1,连接 BC1,则BC1的长为( ).
A.6 B.8 C.10 D.12
B
A
C
B1
C1
C
5.请在图中画出线段AB以点O为旋转中心逆
时针分别旋转90°,180°,270°时对应
的图形.
A
B
O
AB以点O为旋转中心逆时针分别旋转90°,180°,270°时对应的图形分别是A1B1,
A2B2,
A3B3.
A1
B1
A2
B2
A3
B3
6.如图是某设计师设计的图案的一部分.请你运用
旋转变换的方法,在方格纸中画出将该图形绕点
O顺时针依次旋转90°,180°,270°后的图形,
你会得到一个美丽的中心对称图案.注意涂阴影
时不要涂错位置,否则不会出 现理想的效果.
O
7.如图,在△ ABC中,点E在 BC边上AE=AB,
将线段AC绕点A旋转到AF的位置,使得
∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC.
(2)若∠B=65°,∠C=28°,
求∠FGC的度数.
A
F
B
C
G
E
7.如图,在△ ABC中,点E在 BC边上AE=AB,
将线段AC绕点A旋转到AF的位置,使得
∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC.
A
F
B
C
G
E
∵∠CAF =∠BAE,
(1)证明:
∴∠CAF+∠EAC=∠BAE+∠EAC.
∴∠EAF=∠BAC.
∵AF=AC,
AE=AB,
∴△ABC ≌△AEF
∴EF=BC.
(SAS).
7.如图,在△ ABC中,点E在 BC边上AE=AB,
将线段AC绕点A旋转到AF的位置,使得
∠CAF=∠BAE,连接EF,EF与AC交于点G.
(2)若∠B=65°,∠C=28°,求∠FGC的度数.
A
F
B
C
G
E
(2)
∵AE=AB,
∠B=65°,
∴∠AEB=∠B=65°.
∴∠BAE=50°.
∴∠CAF=50°.
∵△ABC ≌△AEF
∴∠F=∠C=28°.
∵∠FGC=∠F+∠CAF,
∴∠FGC=28°+50°
=78°.
今天作业
教科书习题 23.1 第 1, 4,5 题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
23.1图形的旋转(2)
学习目标: 1.理解选择不同的旋转中心、不同的旋转角度对某 一图案作旋转,会出现不同的效果,掌握根据需 要用旋转的知识设计出美丽的图案; 2.复习图形旋转的基本性质,着重强调旋转中心和 旋转角,然后应用已学的知识作图,设计出美丽 的图案.
学习重点: 根据需要设计美丽图案.
课件说明
学生在上节课已经学习了旋转概念、旋转的性质.这 为本节学习奠定了一定的基础.这节课就来具体应用 一下.选择不同的旋转中心,不同的旋转角度,旋转 同一个图形,观察出现的不同效果.
选择不同的旋转中心或不同的旋转角,画出一个图形旋转后的图形.
课件说明
(1)旋转中心不变,改变旋转角(如图).
问题1 让我们一起来欣赏一下美丽的图案,体会一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
O
O
β
α
探究新知
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
探究新知
(3)美丽的图案是这样形成的.
探究新知
问题2 如图,△AOB 绕 O 点旋转后,G 点是 B 点的对应点,作出 △AOB 旋转后的三角形.
G
O
A
B
探究新知
问题3 画出下图所示的四边形 ABCD 以 O 点为中心,旋转角分别为 30°,60°的旋转图形.
O
A
B
C
D
探究新知
问题3 画出下图所示的四边形 ABCD 以O点为中心,旋转角分别为 30°,60°的旋转图形.
A
B
C
D
O
A′
B′
C′
D′
O
A
B
C
D
A′
D′
C′
B′
顺时针旋转 60°
顺时针旋转 30°
问题3 画出下图所示的四边形 ABCD以O点为中心,旋转角分别为 30°,60°的旋转图形.
O
A
B
C
D
B′
A′
D′
C′
O
A
B
C
D
B′
A′
D′
C′
逆时针旋转 60°
逆时针旋转 30°
问题4 画出下图所示的四边形 ABCD 分别以 O1,O2 为中心,旋转角都为 30°的旋转图形.
探究新知
A
B
C
D
O1
O2
问题4 画出下图所示的四边形 ABCD 分别以 O1,O2 为中心,旋转角都为 30°的旋转图形.
A
B
C
D
O1
A′
B′
C′
D′
A
B
C
D
O2
A′
B′
D′
C′
绕 O1 顺时针旋转 30°
绕 O2 顺时针旋转 30°
问题4 画出下图所示的四边形 ABCD 分别以 O1, O2 为中心,旋转角都为 30°的旋转图形.
A
B
C
D
O1
A′
B′
C′
D′
A
B
C
D
O2
D′
A′
B′
C′
绕 O1 逆时针旋转 30°
绕 O2 逆时针旋转 30°
O
例1 如下图是某一种花的花瓣和中心,现以 O 为旋转中心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.
例题解析
例2 如图,如果这种花的一片花瓣,绕旋转中心点O′旋转,请同学画出旋转后的图形.
O′
例题解析
把一个三角形进行旋转:
(1)选择不同的旋转中心,不同的旋转角,看看旋 转的效果;
巩固练习
(2)改变三角形的形状,看看旋转的效果.
3.巩固练习
归纳小结
(1)本节课学了哪些主要内容? (2)怎样画一个图形关于一个点的旋转图形?
1.下列运动形式属于旋转的是( ).
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
C
巩固新知
2.点A(4,2)经过某种图形变换后得到点
B(-2,4),这种图形变换可以是( )
A.关于x轴对称
B.关于y轴对称
C.绕原点逆时针旋转90°
D.绕原点顺时针旋转90°
C
3.如图,线段AB 绕着点O旋转一定的角度
得线段A'B'.下列结论错误的是( ).
A.AB=A'B' B. ∠AOA'=∠BOB'
C.OB=OB' D. ∠AOB'=100°
D
A
B
O
A'
B'
4.如图 ,在△ABC中,∠BAC=30°,AB=8,
AC=6.将 △ ABC绕点A逆时针旋转60°得
到△AB1C1,连接 BC1,则BC1的长为( ).
A.6 B.8 C.10 D.12
B
A
C
B1
C1
C
5.请在图中画出线段AB以点O为旋转中心逆
时针分别旋转90°,180°,270°时对应
的图形.
A
B
O
AB以点O为旋转中心逆时针分别旋转90°,180°,270°时对应的图形分别是A1B1,
A2B2,
A3B3.
A1
B1
A2
B2
A3
B3
6.如图是某设计师设计的图案的一部分.请你运用
旋转变换的方法,在方格纸中画出将该图形绕点
O顺时针依次旋转90°,180°,270°后的图形,
你会得到一个美丽的中心对称图案.注意涂阴影
时不要涂错位置,否则不会出 现理想的效果.
O
7.如图,在△ ABC中,点E在 BC边上AE=AB,
将线段AC绕点A旋转到AF的位置,使得
∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC.
(2)若∠B=65°,∠C=28°,
求∠FGC的度数.
A
F
B
C
G
E
7.如图,在△ ABC中,点E在 BC边上AE=AB,
将线段AC绕点A旋转到AF的位置,使得
∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC.
A
F
B
C
G
E
∵∠CAF =∠BAE,
(1)证明:
∴∠CAF+∠EAC=∠BAE+∠EAC.
∴∠EAF=∠BAC.
∵AF=AC,
AE=AB,
∴△ABC ≌△AEF
∴EF=BC.
(SAS).
7.如图,在△ ABC中,点E在 BC边上AE=AB,
将线段AC绕点A旋转到AF的位置,使得
∠CAF=∠BAE,连接EF,EF与AC交于点G.
(2)若∠B=65°,∠C=28°,求∠FGC的度数.
A
F
B
C
G
E
(2)
∵AE=AB,
∠B=65°,
∴∠AEB=∠B=65°.
∴∠BAE=50°.
∴∠CAF=50°.
∵△ABC ≌△AEF
∴∠F=∠C=28°.
∵∠FGC=∠F+∠CAF,
∴∠FGC=28°+50°
=78°.
今天作业
教科书习题 23.1 第 1, 4,5 题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
