第23章旋转 单元小结 课件(共32张PPT)
文档属性
| 名称 | 第23章旋转 单元小结 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
人教版 九年级上册
第23章 旋转 小结
学习目标:
1.总结和复习图形旋转、中心对称的基本性质的应
用及两个点关于原点对称时坐标之间的关系;
2.注意复习平移、轴对称、旋转的联系和区别,旋
转和中心对称的联系和区别,运用图形旋转、中
心对称的基本性质解一些简单问题.
教学重点:
复习图形旋转的基本性质和中心对称的基本性质及两个点关于原点对称时,它们坐标之间的关系.
课件说明
本章先学习了旋转的有关知识,要求能够从旋转的角度观察图形,进而认识特殊的旋转——中心对称,最后运用轴对称、平移、旋转的组合进行图案设计.
课件说明
(1)定义:在平面内,将某个图形绕一个 沿某方向转动一个 ,这样的图形变换称为旋转;这个定点称为 ,转动的角度称为 .
1.图形的旋转
(2)旋转的要素:
定点
角度
旋转中心
旋转角
旋转中心
旋转方向
旋转角
图形的旋转由 、
和 所决定.
知识回顾
③对应点到旋转中心的距离 .
①经过旋转,图形上的每一个点都绕 沿
相同方向旋转了相同的 .
②任意一对对应点与旋转中心的连线所成的角都是 .
(3)旋转的特征:
旋转中心
角度
旋转角
相等
知识回顾
图形的旋转由 、 和 所决定.
(1)定义:在平面内,将某个图形绕一个 沿某方向转动一个 ,这样的图形变换称为旋转;这个定点称为 ,转动的角度称为 .
1.图形的旋转
③对应点到旋转中心的距离 .
①经过旋转,图形上的每一个点都绕 沿
相同方向旋转了相同的 .
②任意一对对应点与旋转中心的连线所成的角都是 .
(2)旋转的要素:
(3)旋转的特征:
定点
角度
旋转中心
旋转角
旋转中心
旋转方向
旋转中心
旋转角
角度
旋转角
相等
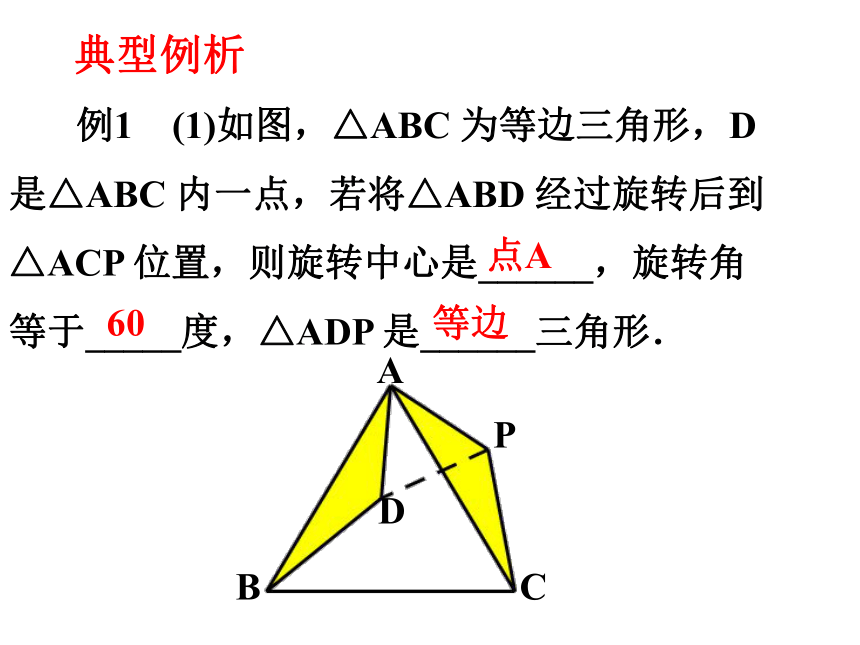
例1 (1)如图,△ABC 为等边三角形,D 是△ABC 内一点,若将△ABD 经过旋转后到△ACP 位置,则旋转中心是______,旋转角等于_____度,△ADP 是______三角形.
A
B
D
P
C
典型例析
点A
60
等边
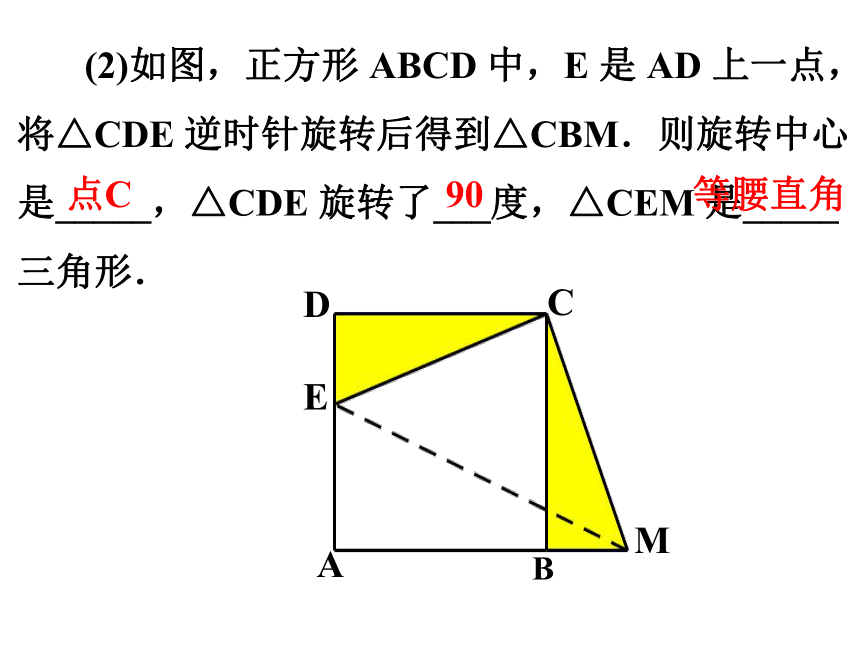
(2)如图,正方形 ABCD 中,E 是 AD 上一点,
将△CDE 逆时针旋转后得到△CBM.则旋转中心是_____,△CDE 旋转了___度,△CEM 是_____三角形.
D
A
E
B
C
M
点C
90
等腰直角
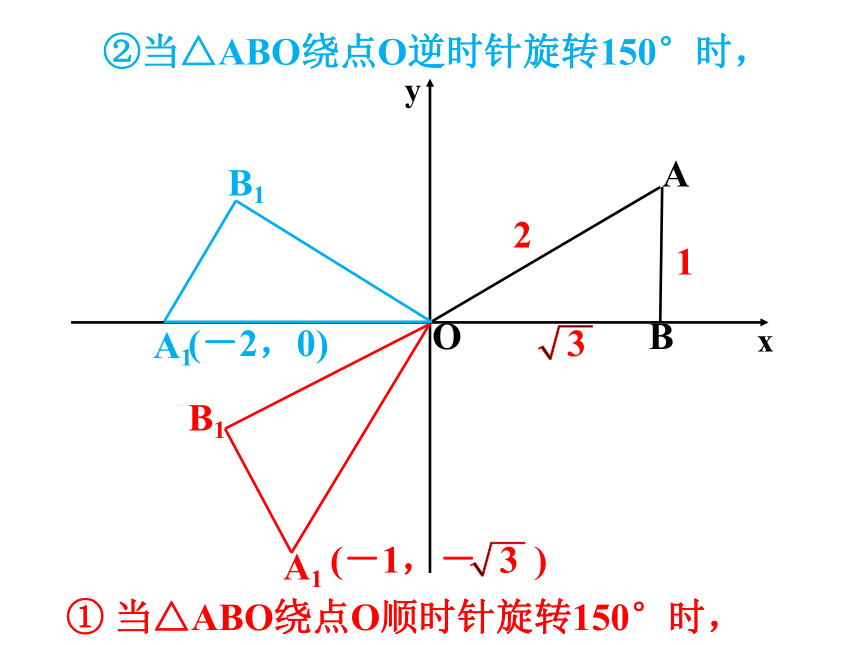
例2.如图,△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1 的坐标为( )
A.(-1,- )
B.(-1,- )或(-2,0)
C.(- ,-1)或(0,-2)
D.(- ,-1)
3
3
3
3
3
B
提示:
旋转150°要分旋转方向讨论
x
y
O
A
B
②当△ABO绕点O逆时针旋转150°时,
① 当△ABO绕点O顺时针旋转150°时,
B1
A1
B1
A1
1
2
3
(-1,- )
3
(-2,0)
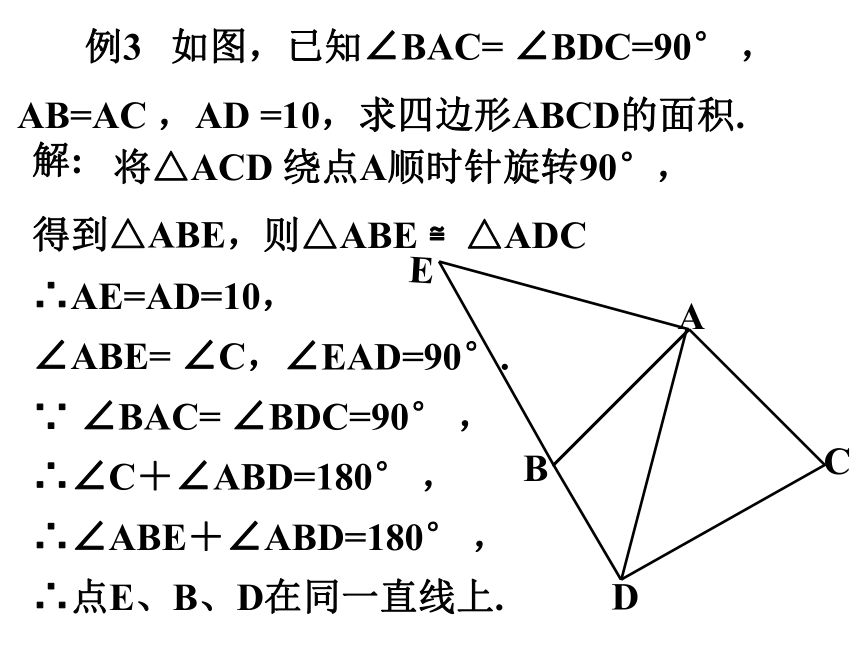
例3 如图,已知∠BAC= ∠BDC=90° ,AB=AC ,AD =10,求四边形ABCD的面积.
D
A
B
C
E
解:
将△ACD 绕点A顺时针旋转90°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD=10,
∠ABE= ∠C,
∵ ∠BAC= ∠BDC=90° ,
∴∠C+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
∠EAD=90°.
D
A
B
C
E
解:
将△ACD 绕点A顺时针旋转90°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD=10,
∠ABE= ∠C,
∵ ∠BAC= ∠BDC=90° ,
∴∠C+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
∴S四边形ABCD=
S△ACD +S△ABD
=S△ABE +S△ABD
=S△ADE
=50.
= AE · AD
1
2
= ×10×10
1
2
∠EAD=90°.
1.下列图形中,不是旋转对称图形的为( ).
A. B. C. D.
B
练习巩固
2.下列图形中,既是轴对称图形,又是中心对
称图形的是( ).
A B C D
D
3.在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为( )
A.(3,4) B.(-4,3)
C.(-3,4) D.(4,-3)
C
2.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
A.30° B.35° C.40° D.50°
A
4.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
A.60° B.75°
C.85° D.90°
C
5. 小明把如图1(1)所示的扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌倒过来,如图1(2),然后小明很快辨认出被倒过来的那张扑克牌是( )
A.方块5 B.梅花6 C.红桃7 D.黑桃8
D
6.如图,在平面直角坐标系中,点B在第一象限,
点A在x轴正半轴上,∠AOB=∠B=30°,OA=2.
将△AOB绕点O逆时针旋转90°,点B的对应点
B'的坐标是( ).
A.(-1, ) B.(- ,3)
C.(- , ) D.(-3, )
3
2+
3
3
3
3
2+
x
y
O
A
B
B'
C
7.如图,在平面直角坐标系中, Rt△ABC的直
角顶点C的坐标为(1,0),点A在x轴正半轴上,
且AC=2.将△ ABC先绕点C逆时针旋转90°,
再向左平移3个单位,则变换后点A的应对点的
坐标为 .
x
y
O
A
B
C
(-3, 2)
6.如图,△ABC 中,∠BAC=90°,AB=AC,P是BC的中点,E是AB上的任意一点,将△PAE绕点P顺时针旋转90°得到△PCF(点F在AC上),则下列结论正确的是 .(填序号)
①EF=AP;
②△EPF为等腰直角三角形;
③AE=CF;
④S四边形AEPF= S△ABC.
②
③
④
1
2
A
B
C
P
E
F
7.如图,△ABC按顺时针方向旋转一定角度后得
到△ADE.已知∠B=19°, ∠ ACB=37°.
(1)旋转中心是哪一点 旋转角是哪个角
旋转角等于多少度
(2)经过旋转,点B,C分别旋转到什么位
(3)AB与AD的长有什么关系 AC与AE
(4) ∠BAD与∠CAE 有什么关系
B
A
C
D
E
7.如图,△ABC按顺时针方向旋转一定角度后得
到△ADE.已知∠B=19°, ∠ ACB=37°.
(1)旋转中心是哪一点 旋转角是哪个角
旋转角等于多少度
(2)经过旋转,点B,C分别旋转到什么位置
B
A
C
D
E
答:(1)旋转中心是点A,旋转角是∠ BAD,
旋转角等于124度;
(2)经过旋转,点B,C
分别旋转到点D,点E;
7.如图,△ABC按顺时针方向旋转一定角度后得
到△ADE.已知∠B=19°, ∠ ACB=37°.
(3)AB与AD的长有什么关系 AC与AE
(4) ∠BAD与∠CAE 有什么关系
B
A
C
D
E
(3)AB=AD;AC=AE;
(4) ∠BAD=∠CAE.
8.已知:△ABC 中,A(-2,3),B(-3,1),
C(-1,2).请画出△ABC 关于原点 O 对称的△A1B1C1.
x
y
O
A
B
C
A1
B1
C1
9.如图,网格中小正方形的边长均为1,已知四
边形ABCD的顶点均在格点上.
(1)求作四边形A1B1C1D1,使四边形 A1B1C1D1与
四边形ABCD关于点O成中心对称图形.
(2)在(1)的基础上,连接A1D,求A1D的长.
A
D
B
C
O
A1
D1
C1
B1
(2)
∵A1B1=4,
DB1=7,
∠A1B1D=90°,
∴A1D2=
+DB12
A1B12
=42+72
=65
∴A1D=
65
四边形
A1B1C1D1
即为所求;
10.如图,已知△ABC 是等边三角形,
∠BDC=120° ,求证:BD+DC=AD.
D
A
B
C
证明:
将△ACD 绕点A顺时针旋转60°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD,
∠ABE= ∠ACD,
∠EAD=60°.
E
∵ ∠BAC=60°, ∠BDC=120° ,
∴∠ACD+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
D
A
B
C
证明:
将△ACD 绕点A顺时针旋转60°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD,
∠ABE= ∠ACD,
∠EAD=60°.
E
∵ ∠BAC=60°, ∠BDC=120° ,
∴∠ACD+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
∴△ACD 是等边三角形.
∴DE=AD
∵DE=BD+BE,
BE=CD,
∴BD+CD=DE .
∴BD+CD=AD .
1.平移、轴对称和旋转有什么区别与联系?
2.旋转和中心对称有什么区别与联系?
3.怎样利用旋转的定义和性质作图?
小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 九年级上册
第23章 旋转 小结
学习目标:
1.总结和复习图形旋转、中心对称的基本性质的应
用及两个点关于原点对称时坐标之间的关系;
2.注意复习平移、轴对称、旋转的联系和区别,旋
转和中心对称的联系和区别,运用图形旋转、中
心对称的基本性质解一些简单问题.
教学重点:
复习图形旋转的基本性质和中心对称的基本性质及两个点关于原点对称时,它们坐标之间的关系.
课件说明
本章先学习了旋转的有关知识,要求能够从旋转的角度观察图形,进而认识特殊的旋转——中心对称,最后运用轴对称、平移、旋转的组合进行图案设计.
课件说明
(1)定义:在平面内,将某个图形绕一个 沿某方向转动一个 ,这样的图形变换称为旋转;这个定点称为 ,转动的角度称为 .
1.图形的旋转
(2)旋转的要素:
定点
角度
旋转中心
旋转角
旋转中心
旋转方向
旋转角
图形的旋转由 、
和 所决定.
知识回顾
③对应点到旋转中心的距离 .
①经过旋转,图形上的每一个点都绕 沿
相同方向旋转了相同的 .
②任意一对对应点与旋转中心的连线所成的角都是 .
(3)旋转的特征:
旋转中心
角度
旋转角
相等
知识回顾
图形的旋转由 、 和 所决定.
(1)定义:在平面内,将某个图形绕一个 沿某方向转动一个 ,这样的图形变换称为旋转;这个定点称为 ,转动的角度称为 .
1.图形的旋转
③对应点到旋转中心的距离 .
①经过旋转,图形上的每一个点都绕 沿
相同方向旋转了相同的 .
②任意一对对应点与旋转中心的连线所成的角都是 .
(2)旋转的要素:
(3)旋转的特征:
定点
角度
旋转中心
旋转角
旋转中心
旋转方向
旋转中心
旋转角
角度
旋转角
相等
例1 (1)如图,△ABC 为等边三角形,D 是△ABC 内一点,若将△ABD 经过旋转后到△ACP 位置,则旋转中心是______,旋转角等于_____度,△ADP 是______三角形.
A
B
D
P
C
典型例析
点A
60
等边
(2)如图,正方形 ABCD 中,E 是 AD 上一点,
将△CDE 逆时针旋转后得到△CBM.则旋转中心是_____,△CDE 旋转了___度,△CEM 是_____三角形.
D
A
E
B
C
M
点C
90
等腰直角
例2.如图,△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1 的坐标为( )
A.(-1,- )
B.(-1,- )或(-2,0)
C.(- ,-1)或(0,-2)
D.(- ,-1)
3
3
3
3
3
B
提示:
旋转150°要分旋转方向讨论
x
y
O
A
B
②当△ABO绕点O逆时针旋转150°时,
① 当△ABO绕点O顺时针旋转150°时,
B1
A1
B1
A1
1
2
3
(-1,- )
3
(-2,0)
例3 如图,已知∠BAC= ∠BDC=90° ,AB=AC ,AD =10,求四边形ABCD的面积.
D
A
B
C
E
解:
将△ACD 绕点A顺时针旋转90°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD=10,
∠ABE= ∠C,
∵ ∠BAC= ∠BDC=90° ,
∴∠C+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
∠EAD=90°.
D
A
B
C
E
解:
将△ACD 绕点A顺时针旋转90°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD=10,
∠ABE= ∠C,
∵ ∠BAC= ∠BDC=90° ,
∴∠C+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
∴S四边形ABCD=
S△ACD +S△ABD
=S△ABE +S△ABD
=S△ADE
=50.
= AE · AD
1
2
= ×10×10
1
2
∠EAD=90°.
1.下列图形中,不是旋转对称图形的为( ).
A. B. C. D.
B
练习巩固
2.下列图形中,既是轴对称图形,又是中心对
称图形的是( ).
A B C D
D
3.在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为( )
A.(3,4) B.(-4,3)
C.(-3,4) D.(4,-3)
C
2.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
A.30° B.35° C.40° D.50°
A
4.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
A.60° B.75°
C.85° D.90°
C
5. 小明把如图1(1)所示的扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌倒过来,如图1(2),然后小明很快辨认出被倒过来的那张扑克牌是( )
A.方块5 B.梅花6 C.红桃7 D.黑桃8
D
6.如图,在平面直角坐标系中,点B在第一象限,
点A在x轴正半轴上,∠AOB=∠B=30°,OA=2.
将△AOB绕点O逆时针旋转90°,点B的对应点
B'的坐标是( ).
A.(-1, ) B.(- ,3)
C.(- , ) D.(-3, )
3
2+
3
3
3
3
2+
x
y
O
A
B
B'
C
7.如图,在平面直角坐标系中, Rt△ABC的直
角顶点C的坐标为(1,0),点A在x轴正半轴上,
且AC=2.将△ ABC先绕点C逆时针旋转90°,
再向左平移3个单位,则变换后点A的应对点的
坐标为 .
x
y
O
A
B
C
(-3, 2)
6.如图,△ABC 中,∠BAC=90°,AB=AC,P是BC的中点,E是AB上的任意一点,将△PAE绕点P顺时针旋转90°得到△PCF(点F在AC上),则下列结论正确的是 .(填序号)
①EF=AP;
②△EPF为等腰直角三角形;
③AE=CF;
④S四边形AEPF= S△ABC.
②
③
④
1
2
A
B
C
P
E
F
7.如图,△ABC按顺时针方向旋转一定角度后得
到△ADE.已知∠B=19°, ∠ ACB=37°.
(1)旋转中心是哪一点 旋转角是哪个角
旋转角等于多少度
(2)经过旋转,点B,C分别旋转到什么位
(3)AB与AD的长有什么关系 AC与AE
(4) ∠BAD与∠CAE 有什么关系
B
A
C
D
E
7.如图,△ABC按顺时针方向旋转一定角度后得
到△ADE.已知∠B=19°, ∠ ACB=37°.
(1)旋转中心是哪一点 旋转角是哪个角
旋转角等于多少度
(2)经过旋转,点B,C分别旋转到什么位置
B
A
C
D
E
答:(1)旋转中心是点A,旋转角是∠ BAD,
旋转角等于124度;
(2)经过旋转,点B,C
分别旋转到点D,点E;
7.如图,△ABC按顺时针方向旋转一定角度后得
到△ADE.已知∠B=19°, ∠ ACB=37°.
(3)AB与AD的长有什么关系 AC与AE
(4) ∠BAD与∠CAE 有什么关系
B
A
C
D
E
(3)AB=AD;AC=AE;
(4) ∠BAD=∠CAE.
8.已知:△ABC 中,A(-2,3),B(-3,1),
C(-1,2).请画出△ABC 关于原点 O 对称的△A1B1C1.
x
y
O
A
B
C
A1
B1
C1
9.如图,网格中小正方形的边长均为1,已知四
边形ABCD的顶点均在格点上.
(1)求作四边形A1B1C1D1,使四边形 A1B1C1D1与
四边形ABCD关于点O成中心对称图形.
(2)在(1)的基础上,连接A1D,求A1D的长.
A
D
B
C
O
A1
D1
C1
B1
(2)
∵A1B1=4,
DB1=7,
∠A1B1D=90°,
∴A1D2=
+DB12
A1B12
=42+72
=65
∴A1D=
65
四边形
A1B1C1D1
即为所求;
10.如图,已知△ABC 是等边三角形,
∠BDC=120° ,求证:BD+DC=AD.
D
A
B
C
证明:
将△ACD 绕点A顺时针旋转60°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD,
∠ABE= ∠ACD,
∠EAD=60°.
E
∵ ∠BAC=60°, ∠BDC=120° ,
∴∠ACD+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
D
A
B
C
证明:
将△ACD 绕点A顺时针旋转60°,
得到△ABE,
则△ABE ≌△ADC
∴AE=AD,
∠ABE= ∠ACD,
∠EAD=60°.
E
∵ ∠BAC=60°, ∠BDC=120° ,
∴∠ACD+∠ABD=180° ,
∴∠ABE+∠ABD=180° ,
∴点E、B、D在同一直线上.
∴△ACD 是等边三角形.
∴DE=AD
∵DE=BD+BE,
BE=CD,
∴BD+CD=DE .
∴BD+CD=AD .
1.平移、轴对称和旋转有什么区别与联系?
2.旋转和中心对称有什么区别与联系?
3.怎样利用旋转的定义和性质作图?
小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
