苏教版2019高中数学必修1 第1章 集合 §1.3 交集、并集 课件(共61张PPT)
文档属性
| 名称 | 苏教版2019高中数学必修1 第1章 集合 §1.3 交集、并集 课件(共61张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 09:29:36 | ||
图片预览







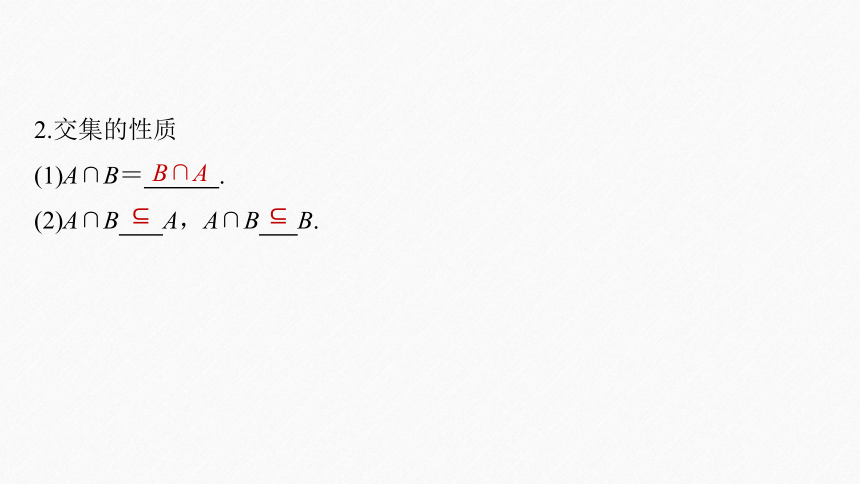



文档简介
(共61张PPT)
§1.3 交集、并集
第1章 集 合
学习目标
1.理解两个集合的并集与交集的含义,会求两个简单集合的并集和交集.
2.能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
3.掌握区间的表示方法.
导语
通过上节课的学习,我们知道集合A在集合S的补集 SA是由给定的两个集合A,S得到的一个新集合.这种用两个给定集合按照某种规则得到一个新集合的过程,称为集合的运算.本节课我们学习集合的另两种运算:集合的交集、补集.
课时对点练
一、交集
二、并集
三、区间及其表示
随堂演练
内容索引
交集
一
问题1 某超市进了两次货,第一次进的货是圆珠笔、钢笔、橡皮、笔记本、方便面、汽水共6种,第二次进的货是圆珠笔、铅笔、火腿肠、方便面共4种,我们用集合A表示第一次进货的品种,用集合B表示第二次进货的品种,通过观察,你能用集合C表示两次进货一样的品种吗?并讨论集合A,B与集合C的关系.
提示 A={圆珠笔,钢笔,橡皮,笔记本,方便面,汽水},B={圆珠笔,铅笔,火腿肠,方便面},则C={圆珠笔,方便面},容易发现集合C是由所有既属于集合A又属于集合B的元素组成的.
知识梳理
1.交集的概念
自然语言 一般地,由所有属于集合A 属于集合B的元素构成的集合,称为A与B的交集,记作 (读作“A交B”)
符号语言 A∩B=_________________
图形语言
且
A∩B
{x|x∈A,且x∈B}
2.交集的性质
(1)A∩B= .
(2)A∩B A,A∩B B.
B∩A
(1)A∩B仍是一个集合.
(2)文字语言中“所有”的含义:A∩B中任一元素都是A与B的公共元素,A与B的公共元素都属于A∩B.
(3)如果两个集合没有公共元素,不能说两个集合没有交集,而是A∩B= .
注意点:
(1)已知集合A={1,2,3,4},B={y|y=3x-2,x∈A},则A∩B等于
A.{1} B.{4} C.{1,3} D.{1,4}
例1
√
因为集合B中,x∈A,
所以当x=1时,y=3-2=1;
当x=2时,y=3×2-2=4;
当x=3时,y=3×3-2=7;
当x=4时,y=3×4-2=10.
即B={1,4,7,10}.
又因为A={1,2,3,4},所以A∩B={1,4}.
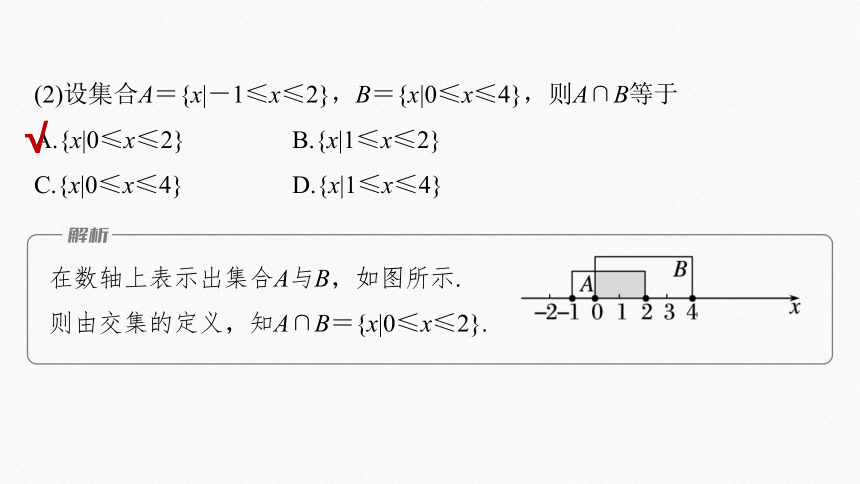
在数轴上表示出集合A与B,如图所示.
则由交集的定义,知A∩B={x|0≤x≤2}.
(2)设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于
A.{x|0≤x≤2} B.{x|1≤x≤2}
C.{x|0≤x≤4} D.{x|1≤x≤4}
√
交集运算的注意点
若A,B是无限连续的数集,多利用数轴来求解.但要注意,利用数轴表示不等式时,含有端点的值用实心点表示,不含有端点的值用空心点表示.
反思感悟
跟踪训练1
(1) 若A={x|1≤x≤10,x∈N},B={x|x2+x-6=0,x∈Z},则图中阴影部分表示的集合为
A.{2} B.{3}
C.{-3,2} D.{-2,3}
易知A={1,2,3,4,5,6,7,8,9,10},B={-3,2},图中阴影部分表示的集合为A∩B={2}.
√
因为A={x|-23},
所以A∩B={x|-2(2)若集合A={x|-23},则A∩B等于
A.{x|-2C.{x|-1√
并集
二
问题2 对于问题1中的集合A与集合B,你能用集合D表示两次一共进货的品种吗?并讨论集合A,B与集合D的关系.
提示 由A={圆珠笔,钢笔,橡皮,笔记本,方便面,汽水},B={圆珠笔,铅笔,火腿肠,方便面}知,集合D={圆珠笔,钢笔,橡皮,笔记本,方便面,汽水,铅笔,火腿肠},可见,集合D是由所有属于集合A或属于集合B的元素组成的.
知识梳理
1.并集的概念
自然语言 一般地,由所有属于集合A 属于集合B的元素构成的集合,称为A与B的并集,记作 (读作“A并B”)
符号语言 A∪B=_________________
图形语言
或者
A∪B
{x|x∈A,或x∈B}
2.并集的性质
(1)A∪B B∪A.
(2)A A∪B,B A∪B.
=
(1)A∪B仍是一个集合.
(2)并集符号语言中的“或”包含三种情况:①x∈A且x B;②x∈A且x∈B;③x A且x∈B.
(3)对概念中“所有”的理解,要注意集合元素的互异性.
注意点:
(1)若集合A={x|x>-1},B={x|-2A.{x|x>-2} B.{x|x>-1}
C.{x|-2例2
√
在数轴上表示出集合A与B,如图所示,故A∪B={x|x>-2}.
(2)已知集合A={x|-3∵A∪B=A,∴B A,∴分B= 和B≠ 两种情况讨论.
①当B= 时,k+1>2k-1,∴k<2.
②当B≠ 时,则根据题意画数轴如图所示,
(1)并集的运算技巧
①若集合中元素个数有限,则直接根据并集的定义求解,但要注意集合中元素的互异性.
②若集合中元素个数无限,可借助数轴,利用数轴分析法求解,但要注意是否去掉端点值.
反思感悟
(2)利用集合交集、并集的性质解题的技巧
①在进行集合运算时,若条件中出现A∩B=A或A∪B=B,应转化为A B,然后用集合间的关系解决问题,并注意A= 的情况.
②集合运算常用的性质:A∪B=B A B;A∩B=A A B;A∩B=A∪B A=B.
反思感悟
(1)已知集合A={x|-2A.{x|-2C.{x|1跟踪训练2
√
因为集合A={x|-2所以A∪B={x|-2(2)设集合M={x|0由M∩N=M∪N,得N=M.
2
解得t=2.
区间及其表示
三
知识梳理
1.区间概念(a,b为实数,且a定义 名称 符号 数轴表示
{x|a≤x≤b} 闭区间 ______
{x|a{x|a≤x{x|a[a,b]
(a,b)
[a,b)
(a,b]
2.其他区间的表示
定义 R {x|x≥a} {x|x>a} {x|x≤a} {x|x区间 ____________ _________ _________ _________ _________
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
(1)区间只能表示连续的数集,开闭不能混淆.
(2)区间是实数集的一种表示形式,集合的运算仍然成立.
(3)用数轴表示区间时,要特别注意实心点与空心点的区别.
(4)∞是一个符号,而不是一个数.
注意点:
把下列数集用区间表示:
(1){x|x≥-1};
例3
{x|x≥-1}=[-1,+∞).
(2){x|x<0};
{x|x<0}=(-∞,0).
(3){x|-1{x|-1(4){x|0{x|0用区间表示数集的方法
(1)区间左端点值小于右端点值.
(2)区间两端点之间用“,”隔开.
(3)含端点值的一端用中括号,不含端点值的一端用小括号.
(4)以“-∞”“+∞”为区间的一端时,这端必须用小括号.
反思感悟
(1)集合{x|-2跟踪训练3
(-2,0)∪(0,2]
{x|-2=(-2,0)∪(0,2].
(2)已知区间(a2+a+1,7],则实数a的取值范围是________.
(-3,2)
由题意可知a2+a+1<7,
即a2+a-6<0,
解得-3所以实数a的取值范围是(-3,2).
课堂
小结
1.知识清单:
(1)交集、并集的概念及运算.
(2)交集、并集运算的性质.
(3)求参数值或范围.
(4)区间及其表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:由交集、并集的关系求解参数时漏掉对集合为空集的讨论.
随堂演练
1.将集合A={x|1A.(1,3) B.(1,3]
C.[1,3) D.[1,3]
√
1
2
3
4
集合A为左开右闭区间,可表示为(1,3].
2.(多选)满足{1}∪B={1,2}的集合B可能等于
A.{2} B.{1}
C.{1,2} D.{1,2,3}
√
1
2
3
4
∵{1}∪B={1,2},
∴B可能为{2}或{1,2}.
√
3.已知集合M={-1,0,1},N={0,1,2},则M∪N=__________.
1
2
3
4
M∪N表示所有属于M或属于N的元素构成的集合,故M∪N={-1,0,1,2}.
{-1,0,1,2}
4.若集合A={x|-11
2
3
4
R
{x|4≤x<5}
借助数轴可知A∪B=R,A∩B={x|4≤x<5}.
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.已知集合M={-1,0,1},P={0,1,2,3},则图中阴影部分所表示的集合是
A.{0,1} B.{0}
C.{-1,2,3} D.{-1,0,1,2,3}
√
由Venn图,可知阴影部分所表示的集合是M∪P.
因为M={-1,0,1},P={0,1,2,3},
故M∪P={-1,0,1,2,3}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知集合A={x|x≤5,x∈R},B={x|x>1,x∈R},那么A∩B等于
A.{1,2,3,4,5} B.{2,3,4,5}
C.{2,3,4} D.{x|1√
∵A={x|x≤5,x∈R},B={x|x>1,x∈R},
∴A∩B={x|11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则A∩ UB等于
A.{3} B.{2,5}
C.{1,4,6} D.{2,3,5}
√
由题意知, UB={2,5},
则A∩( UB)={2,3,5}∩{2,5}={2,5}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.(多选)若集合M N,则下列结论正确的是
A.M∩N=M B.M∪N=N
C.M M∩N D.( NM)∩N=M
√
因为M N,
所以M∩N=M,M∪N=N,M M∩N,( NM)∩N= NM,故选ABC.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.已知集合A={x|1≤x<3},B={y|y≤m},且A∩B= ,则实数m应满足
A.m<1 B.m≤1 C.m≥3 D.m>3
√
∵集合A={x|1≤x<3},B={y|y≤m},A∩B= ,∴m<1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)若集合A={-1,2,3,4},B={1,2,3,5},则
A.A∩B={2,3}
B.A∪B={-1,1,2,3,4,5}
C.A B
D.A∩B=A∪B
√
因为A={-1,2,3,4},B={1,2,3,5},
所以A∩B={2,3},A∪B={-1,1,2,3,4,5},故选A,B.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设全集U=R,A=(0,+∞),B=(1,+∞),则A∩( UB)=_____.
∵U=R,B=(1,+∞),
∴ UB=(-∞,1].
又∵A=(0,+∞),
∴A∩( UB)=(0,+∞)∩(-∞,1]=(0,1].
(0,1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是__________.(用区间表示)
因为A∪B=R,画出数轴(图略)可知表示实数a的点必须与表示1的点重合或在表示1的点的左边,所以a≤1.
(-∞,1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知集合A={x|3≤x<7},B={x|2(1)A∪B;
由集合A={x|3≤x<7},B={x|2得到A∪B={x|21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)C∩B.
由集合B={x|2则C∩B={x|21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知集合A={x|1(1)当m=-1时,求A∪B;
当m=-1时,B={x|-1∴A∪B={x|-1(2)若A∩B=A,求实数m的取值范围.
∵A∩B=A,∴A B,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.设集合S={x|x<-1,或x>5},T={x|aA.-3C.a≤-3或a≥-1 D.a<-3或a>-1
√
∴-31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知全集U,集合M,N是U的子集,且M?N,则下列结论中一定正确的是
A.( UM)∪( UN)=U
B.M∩( UN)=
C.M∪( UN)=U
D.( UM)∩N=
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
集合M,N是U的子集,且M?N,
对于A,( UM)∪( UN)= UM,故A不正确;
对于B,M∩( UN)= ,故B正确;
对于C,M∪( UN)≠U,不包括属于N且不属于M的部分,故C不正确;
对于D,( UM)∩N≠ ,其交集为属于N且不属于M的部分,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.已知集合A={x|x<1,或x>5},B={x|a≤x≤b},且A∪B=R,A∩B={x|5A.-1 B.7
C.-4 D.-5
√
如图所示,
可知a=1,b=6,2a-b=-4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知集合A={-2,3,4,6},集合B={3,a,a2},若B A,则实数a=_____;若A∩B={3,4},则实数a=______.
∵集合A={-2,3,4,6},
集合B={3,a,a2},B A,∴a=-2.
∵A∩B={3,4},∴a=4或a2=4,
∴a=±2或4.
当a=-2时,B={3,-2,4},不符合题意;
当a=2或4时,B={3,2,4}或{3,4,16},符合题意,
∴实数a=2或4.
2或4
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_____.
设所求人数为x,则只喜爱乒乓球运动的人数为10-(15-x)=x-5,故15+(x-5)=30-8,解得x=12.
12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.在①B ( RA),②( RA)∪B=R,③A∩B=B这三个条件中任选一个,补充在下面问题中.若问题中的实数a存在,求a的取值范围;若问题中的实数a不存在,请说明理由.
已知集合A={x|1≤x≤4},B={x|a+11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
集合A={x|1≤x≤4}.
若选①: RA={x|x<1,或x>4},
由B ( RA)得,
当B= 时,a+1≥2a-1,解得a≤2;
解得a∈ 或a≥3,
所以实数a的取值范围是[3,+∞).
综上,存在实数a,使得B ( RA),且a的取值范围为(-∞,2]∪[3,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若选②:
RA={x|x<1,或x>4},
由( RA)∪B=R,得B≠ ,
所以不存在实数a,使得( RA)∪B=R.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若选③:
由A∩B=B,可知B A,
当B= 时,a+1≥2a-1,解得a≤2;
综上,存在实数a,使得A∩B=B,
§1.3 交集、并集
第1章 集 合
学习目标
1.理解两个集合的并集与交集的含义,会求两个简单集合的并集和交集.
2.能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
3.掌握区间的表示方法.
导语
通过上节课的学习,我们知道集合A在集合S的补集 SA是由给定的两个集合A,S得到的一个新集合.这种用两个给定集合按照某种规则得到一个新集合的过程,称为集合的运算.本节课我们学习集合的另两种运算:集合的交集、补集.
课时对点练
一、交集
二、并集
三、区间及其表示
随堂演练
内容索引
交集
一
问题1 某超市进了两次货,第一次进的货是圆珠笔、钢笔、橡皮、笔记本、方便面、汽水共6种,第二次进的货是圆珠笔、铅笔、火腿肠、方便面共4种,我们用集合A表示第一次进货的品种,用集合B表示第二次进货的品种,通过观察,你能用集合C表示两次进货一样的品种吗?并讨论集合A,B与集合C的关系.
提示 A={圆珠笔,钢笔,橡皮,笔记本,方便面,汽水},B={圆珠笔,铅笔,火腿肠,方便面},则C={圆珠笔,方便面},容易发现集合C是由所有既属于集合A又属于集合B的元素组成的.
知识梳理
1.交集的概念
自然语言 一般地,由所有属于集合A 属于集合B的元素构成的集合,称为A与B的交集,记作 (读作“A交B”)
符号语言 A∩B=_________________
图形语言
且
A∩B
{x|x∈A,且x∈B}
2.交集的性质
(1)A∩B= .
(2)A∩B A,A∩B B.
B∩A
(1)A∩B仍是一个集合.
(2)文字语言中“所有”的含义:A∩B中任一元素都是A与B的公共元素,A与B的公共元素都属于A∩B.
(3)如果两个集合没有公共元素,不能说两个集合没有交集,而是A∩B= .
注意点:
(1)已知集合A={1,2,3,4},B={y|y=3x-2,x∈A},则A∩B等于
A.{1} B.{4} C.{1,3} D.{1,4}
例1
√
因为集合B中,x∈A,
所以当x=1时,y=3-2=1;
当x=2时,y=3×2-2=4;
当x=3时,y=3×3-2=7;
当x=4时,y=3×4-2=10.
即B={1,4,7,10}.
又因为A={1,2,3,4},所以A∩B={1,4}.
在数轴上表示出集合A与B,如图所示.
则由交集的定义,知A∩B={x|0≤x≤2}.
(2)设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A∩B等于
A.{x|0≤x≤2} B.{x|1≤x≤2}
C.{x|0≤x≤4} D.{x|1≤x≤4}
√
交集运算的注意点
若A,B是无限连续的数集,多利用数轴来求解.但要注意,利用数轴表示不等式时,含有端点的值用实心点表示,不含有端点的值用空心点表示.
反思感悟
跟踪训练1
(1) 若A={x|1≤x≤10,x∈N},B={x|x2+x-6=0,x∈Z},则图中阴影部分表示的集合为
A.{2} B.{3}
C.{-3,2} D.{-2,3}
易知A={1,2,3,4,5,6,7,8,9,10},B={-3,2},图中阴影部分表示的集合为A∩B={2}.
√
因为A={x|-2
所以A∩B={x|-2
A.{x|-2
并集
二
问题2 对于问题1中的集合A与集合B,你能用集合D表示两次一共进货的品种吗?并讨论集合A,B与集合D的关系.
提示 由A={圆珠笔,钢笔,橡皮,笔记本,方便面,汽水},B={圆珠笔,铅笔,火腿肠,方便面}知,集合D={圆珠笔,钢笔,橡皮,笔记本,方便面,汽水,铅笔,火腿肠},可见,集合D是由所有属于集合A或属于集合B的元素组成的.
知识梳理
1.并集的概念
自然语言 一般地,由所有属于集合A 属于集合B的元素构成的集合,称为A与B的并集,记作 (读作“A并B”)
符号语言 A∪B=_________________
图形语言
或者
A∪B
{x|x∈A,或x∈B}
2.并集的性质
(1)A∪B B∪A.
(2)A A∪B,B A∪B.
=
(1)A∪B仍是一个集合.
(2)并集符号语言中的“或”包含三种情况:①x∈A且x B;②x∈A且x∈B;③x A且x∈B.
(3)对概念中“所有”的理解,要注意集合元素的互异性.
注意点:
(1)若集合A={x|x>-1},B={x|-2
C.{x|-2
√
在数轴上表示出集合A与B,如图所示,故A∪B={x|x>-2}.
(2)已知集合A={x|-3
①当B= 时,k+1>2k-1,∴k<2.
②当B≠ 时,则根据题意画数轴如图所示,
(1)并集的运算技巧
①若集合中元素个数有限,则直接根据并集的定义求解,但要注意集合中元素的互异性.
②若集合中元素个数无限,可借助数轴,利用数轴分析法求解,但要注意是否去掉端点值.
反思感悟
(2)利用集合交集、并集的性质解题的技巧
①在进行集合运算时,若条件中出现A∩B=A或A∪B=B,应转化为A B,然后用集合间的关系解决问题,并注意A= 的情况.
②集合运算常用的性质:A∪B=B A B;A∩B=A A B;A∩B=A∪B A=B.
反思感悟
(1)已知集合A={x|-2
√
因为集合A={x|-2
2
解得t=2.
区间及其表示
三
知识梳理
1.区间概念(a,b为实数,且a
{x|a≤x≤b} 闭区间 ______
{x|a
(a,b)
[a,b)
(a,b]
2.其他区间的表示
定义 R {x|x≥a} {x|x>a} {x|x≤a} {x|x
(-∞,+∞)
[a,+∞)
(a,+∞)
(-∞,a]
(-∞,a)
(1)区间只能表示连续的数集,开闭不能混淆.
(2)区间是实数集的一种表示形式,集合的运算仍然成立.
(3)用数轴表示区间时,要特别注意实心点与空心点的区别.
(4)∞是一个符号,而不是一个数.
注意点:
把下列数集用区间表示:
(1){x|x≥-1};
例3
{x|x≥-1}=[-1,+∞).
(2){x|x<0};
{x|x<0}=(-∞,0).
(3){x|-1
(1)区间左端点值小于右端点值.
(2)区间两端点之间用“,”隔开.
(3)含端点值的一端用中括号,不含端点值的一端用小括号.
(4)以“-∞”“+∞”为区间的一端时,这端必须用小括号.
反思感悟
(1)集合{x|-2
(-2,0)∪(0,2]
{x|-2
(2)已知区间(a2+a+1,7],则实数a的取值范围是________.
(-3,2)
由题意可知a2+a+1<7,
即a2+a-6<0,
解得-3
课堂
小结
1.知识清单:
(1)交集、并集的概念及运算.
(2)交集、并集运算的性质.
(3)求参数值或范围.
(4)区间及其表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:由交集、并集的关系求解参数时漏掉对集合为空集的讨论.
随堂演练
1.将集合A={x|1
C.[1,3) D.[1,3]
√
1
2
3
4
集合A为左开右闭区间,可表示为(1,3].
2.(多选)满足{1}∪B={1,2}的集合B可能等于
A.{2} B.{1}
C.{1,2} D.{1,2,3}
√
1
2
3
4
∵{1}∪B={1,2},
∴B可能为{2}或{1,2}.
√
3.已知集合M={-1,0,1},N={0,1,2},则M∪N=__________.
1
2
3
4
M∪N表示所有属于M或属于N的元素构成的集合,故M∪N={-1,0,1,2}.
{-1,0,1,2}
4.若集合A={x|-1
2
3
4
R
{x|4≤x<5}
借助数轴可知A∪B=R,A∩B={x|4≤x<5}.
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.已知集合M={-1,0,1},P={0,1,2,3},则图中阴影部分所表示的集合是
A.{0,1} B.{0}
C.{-1,2,3} D.{-1,0,1,2,3}
√
由Venn图,可知阴影部分所表示的集合是M∪P.
因为M={-1,0,1},P={0,1,2,3},
故M∪P={-1,0,1,2,3}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知集合A={x|x≤5,x∈R},B={x|x>1,x∈R},那么A∩B等于
A.{1,2,3,4,5} B.{2,3,4,5}
C.{2,3,4} D.{x|1
∵A={x|x≤5,x∈R},B={x|x>1,x∈R},
∴A∩B={x|1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则A∩ UB等于
A.{3} B.{2,5}
C.{1,4,6} D.{2,3,5}
√
由题意知, UB={2,5},
则A∩( UB)={2,3,5}∩{2,5}={2,5}.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.(多选)若集合M N,则下列结论正确的是
A.M∩N=M B.M∪N=N
C.M M∩N D.( NM)∩N=M
√
因为M N,
所以M∩N=M,M∪N=N,M M∩N,( NM)∩N= NM,故选ABC.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.已知集合A={x|1≤x<3},B={y|y≤m},且A∩B= ,则实数m应满足
A.m<1 B.m≤1 C.m≥3 D.m>3
√
∵集合A={x|1≤x<3},B={y|y≤m},A∩B= ,∴m<1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)若集合A={-1,2,3,4},B={1,2,3,5},则
A.A∩B={2,3}
B.A∪B={-1,1,2,3,4,5}
C.A B
D.A∩B=A∪B
√
因为A={-1,2,3,4},B={1,2,3,5},
所以A∩B={2,3},A∪B={-1,1,2,3,4,5},故选A,B.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设全集U=R,A=(0,+∞),B=(1,+∞),则A∩( UB)=_____.
∵U=R,B=(1,+∞),
∴ UB=(-∞,1].
又∵A=(0,+∞),
∴A∩( UB)=(0,+∞)∩(-∞,1]=(0,1].
(0,1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知集合A={x|x≤1},B={x|x≥a},且A∪B=R,则实数a的取值范围是__________.(用区间表示)
因为A∪B=R,画出数轴(图略)可知表示实数a的点必须与表示1的点重合或在表示1的点的左边,所以a≤1.
(-∞,1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知集合A={x|3≤x<7},B={x|2
由集合A={x|3≤x<7},B={x|2
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)C∩B.
由集合B={x|2
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知集合A={x|1
当m=-1时,B={x|-1
∵A∩B=A,∴A B,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
11.设集合S={x|x<-1,或x>5},T={x|a
√
∴-3
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知全集U,集合M,N是U的子集,且M?N,则下列结论中一定正确的是
A.( UM)∪( UN)=U
B.M∩( UN)=
C.M∪( UN)=U
D.( UM)∩N=
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
集合M,N是U的子集,且M?N,
对于A,( UM)∪( UN)= UM,故A不正确;
对于B,M∩( UN)= ,故B正确;
对于C,M∪( UN)≠U,不包括属于N且不属于M的部分,故C不正确;
对于D,( UM)∩N≠ ,其交集为属于N且不属于M的部分,故D不正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.已知集合A={x|x<1,或x>5},B={x|a≤x≤b},且A∪B=R,A∩B={x|5
C.-4 D.-5
√
如图所示,
可知a=1,b=6,2a-b=-4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知集合A={-2,3,4,6},集合B={3,a,a2},若B A,则实数a=_____;若A∩B={3,4},则实数a=______.
∵集合A={-2,3,4,6},
集合B={3,a,a2},B A,∴a=-2.
∵A∩B={3,4},∴a=4或a2=4,
∴a=±2或4.
当a=-2时,B={3,-2,4},不符合题意;
当a=2或4时,B={3,2,4}或{3,4,16},符合题意,
∴实数a=2或4.
2或4
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_____.
设所求人数为x,则只喜爱乒乓球运动的人数为10-(15-x)=x-5,故15+(x-5)=30-8,解得x=12.
12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.在①B ( RA),②( RA)∪B=R,③A∩B=B这三个条件中任选一个,补充在下面问题中.若问题中的实数a存在,求a的取值范围;若问题中的实数a不存在,请说明理由.
已知集合A={x|1≤x≤4},B={x|a+1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
集合A={x|1≤x≤4}.
若选①: RA={x|x<1,或x>4},
由B ( RA)得,
当B= 时,a+1≥2a-1,解得a≤2;
解得a∈ 或a≥3,
所以实数a的取值范围是[3,+∞).
综上,存在实数a,使得B ( RA),且a的取值范围为(-∞,2]∪[3,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若选②:
RA={x|x<1,或x>4},
由( RA)∪B=R,得B≠ ,
所以不存在实数a,使得( RA)∪B=R.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若选③:
由A∩B=B,可知B A,
当B= 时,a+1≥2a-1,解得a≤2;
综上,存在实数a,使得A∩B=B,
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
