人教版七年级上册1.5.1 乘方课件(共23张PPT)
文档属性
| 名称 | 人教版七年级上册1.5.1 乘方课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 09:18:48 | ||
图片预览







文档简介
(共23张PPT)
(第1课时 乘方 )
几个不是0的有理数相乘,积的符号是由什么确定的?
积的符号是由负因数的个数确定的,
若负因数的个数为偶数时,积的符号为正;
当负因数的个数为奇数时,积的符号为负.
计算:
思考:
如图,一正方形的边长为a, 则它的面积为 .
a·a
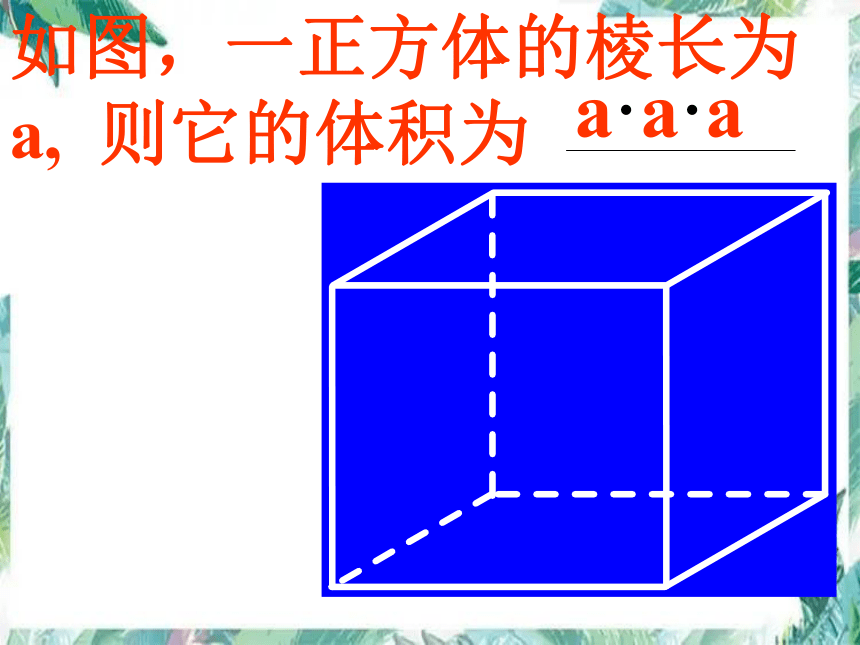
如图,一正方体的棱长为a, 则它的体积为
a·a·a
2个 相加可记为:
3个 相加可记为:
4个 相加可记为:
个 相加可记为:
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
探究新知
个
个
计算时,在这个积中有100个a相乘。这么长的算式有简单的记法吗?
这个式子有什么特点:
100个相同的因数a相乘.
个
100
一般地,n个相同的因数a相乘,
记作 ,读作a的n次方。
a ·a · … ·a ·a
n个
an
记作
an
即
个相同的因数 相乘,即
我们把它记作 ;
即
这种求 个 的积的运算,叫做乘方。
相同因数
乘方的结果叫做幂。
在 中, 叫做底数, 叫做指数。
幂
指数
相同因数的个数
底数
相同因数
读作 的 次方,也可以读作 的 次幂。
指数
底数
幂
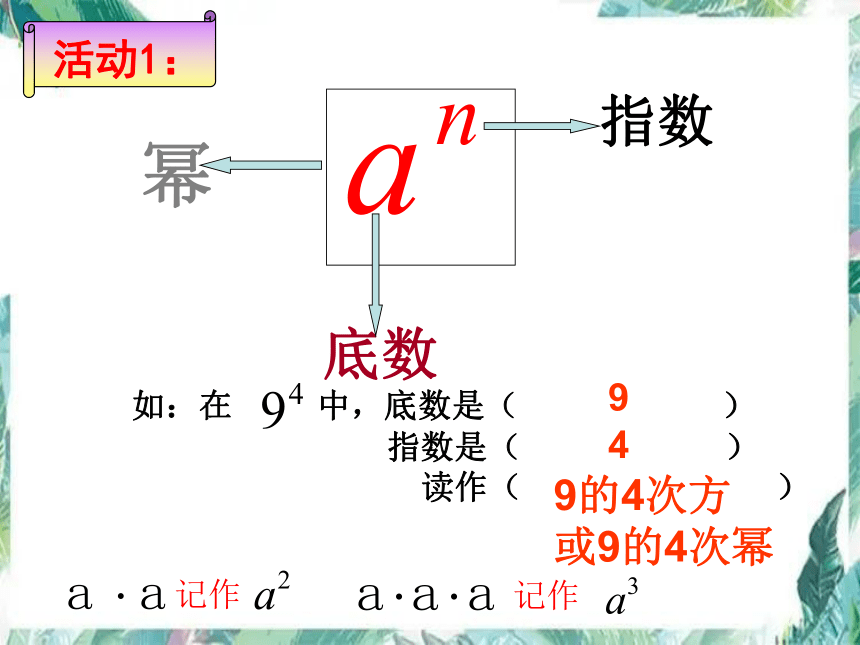
如:在 中,底数是( )
指数是( )
读作( )
9
4
9的4次方
或9的4次幂
活动1:
记作
记作
说出下列各式的底数和指数,并把他们读出来。
说一说:
底数是8,指数3,读作:8的3次方。
底数是-9,指数是5,
读作:-9的5次方。
想一想,说一说:
8
0
123
一个数可以看作这个数本身的一次方,指数1通常省略不写。
0的任何正整数次幂都是0。
指出下列每个的底数和指数。
,6
练一练:
请指出下列各组
数的异同。
注意:
(1)负数的乘方,在书写时一定要把整个负数, 用小括号括起来.这也是辨认底数的方法。
(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来.
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、
练习2:
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
思考:用乘方式子怎么表示 的相反数?
的相反数是
解:
例1:计算
讲解例题:
例2:计算:
解:
如果幂的底数是正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都正数
正数的任何次幂是正数;
得出:
正
负
例3:
9
-32
1
负数的奇次幂是___数
负数的偶次幂是___数。
思考:这四个幂,底数都是负数,为什么两个幂是正数,而另两个是负数呢?是由什么数来确定它们的正负呢?
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数。
正数的任何次幂是正数;
0的任何正整数次幂是0;
归纳:
计算:
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
1
-1
25
-0.001
-27
7、一个数的平方为16,这个数可能是几?一个数的平方可能是零吗?
巩固练习:
回顾与小结
本节课里你学到了什么?
1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的; 2、有理数的乘方的意义和相关概念;
幂的底数是分数或负数时,底数应该添上括号.
3、乘方的性质
(1)负数的奇次幂是负数;
负数的偶次幂是正数;
(2)正数的任何次幂都是正数;
(3)0的任何正整数次幂都是0。
3.乘方的有关运算
进行乘方运算应先确定符号后再计算。
(第1课时 乘方 )
几个不是0的有理数相乘,积的符号是由什么确定的?
积的符号是由负因数的个数确定的,
若负因数的个数为偶数时,积的符号为正;
当负因数的个数为奇数时,积的符号为负.
计算:
思考:
如图,一正方形的边长为a, 则它的面积为 .
a·a
如图,一正方体的棱长为a, 则它的体积为
a·a·a
2个 相加可记为:
3个 相加可记为:
4个 相加可记为:
个 相加可记为:
边长为 的正方形的面积可记为:
那么4个 相乘可记为:
棱长为 的正方体的体积可记为:
个 相乘又可记为:
探究新知
个
个
计算时,在这个积中有100个a相乘。这么长的算式有简单的记法吗?
这个式子有什么特点:
100个相同的因数a相乘.
个
100
一般地,n个相同的因数a相乘,
记作 ,读作a的n次方。
a ·a · … ·a ·a
n个
an
记作
an
即
个相同的因数 相乘,即
我们把它记作 ;
即
这种求 个 的积的运算,叫做乘方。
相同因数
乘方的结果叫做幂。
在 中, 叫做底数, 叫做指数。
幂
指数
相同因数的个数
底数
相同因数
读作 的 次方,也可以读作 的 次幂。
指数
底数
幂
如:在 中,底数是( )
指数是( )
读作( )
9
4
9的4次方
或9的4次幂
活动1:
记作
记作
说出下列各式的底数和指数,并把他们读出来。
说一说:
底数是8,指数3,读作:8的3次方。
底数是-9,指数是5,
读作:-9的5次方。
想一想,说一说:
8
0
123
一个数可以看作这个数本身的一次方,指数1通常省略不写。
0的任何正整数次幂都是0。
指出下列每个的底数和指数。
,6
练一练:
请指出下列各组
数的异同。
注意:
(1)负数的乘方,在书写时一定要把整个负数, 用小括号括起来.这也是辨认底数的方法。
(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来.
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、
练习2:
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
思考:用乘方式子怎么表示 的相反数?
的相反数是
解:
例1:计算
讲解例题:
例2:计算:
解:
如果幂的底数是正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都正数
正数的任何次幂是正数;
得出:
正
负
例3:
9
-32
1
负数的奇次幂是___数
负数的偶次幂是___数。
思考:这四个幂,底数都是负数,为什么两个幂是正数,而另两个是负数呢?是由什么数来确定它们的正负呢?
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数。
正数的任何次幂是正数;
0的任何正整数次幂是0;
归纳:
计算:
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
1
-1
25
-0.001
-27
7、一个数的平方为16,这个数可能是几?一个数的平方可能是零吗?
巩固练习:
回顾与小结
本节课里你学到了什么?
1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的; 2、有理数的乘方的意义和相关概念;
幂的底数是分数或负数时,底数应该添上括号.
3、乘方的性质
(1)负数的奇次幂是负数;
负数的偶次幂是正数;
(2)正数的任何次幂都是正数;
(3)0的任何正整数次幂都是0。
3.乘方的有关运算
进行乘方运算应先确定符号后再计算。
