苏教版2019高中数学必修1 第3章 培优课 基本不等式的综合问题 课件(共64张PPT)
文档属性
| 名称 | 苏教版2019高中数学必修1 第3章 培优课 基本不等式的综合问题 课件(共64张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-14 12:33:51 | ||
图片预览





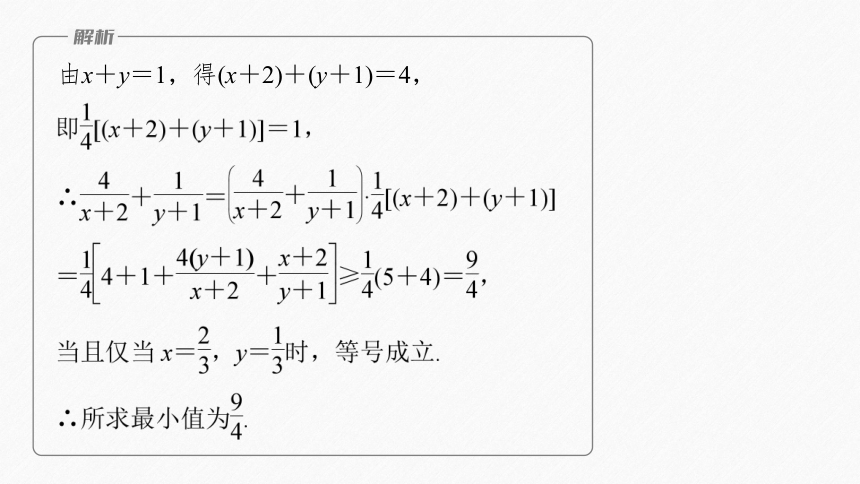

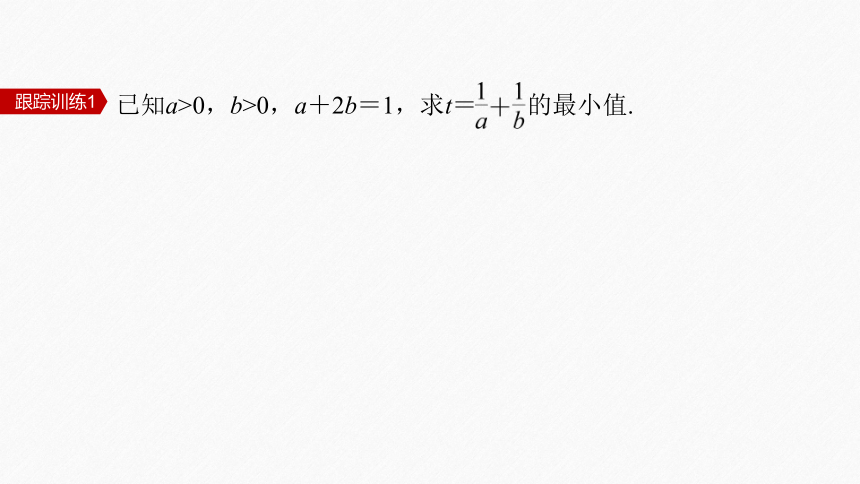




文档简介
(共64张PPT)
培优课 基本不等式的综合问题
第3章 不等式
基本不等式 (a,b≥0)在求最值中的应用广泛,方法
灵活多变,常见考查情形有常数代换法求最值、消元法求最值、换元法求最值等.
课时对点练
一、常数代换法求最值
二、消元法求最值
三、换元法求最值
随堂演练
内容索引
常数代换法求最值
一
例1
√
由x+y=1,得(x+2)+(y+1)=4,
常数代换法解题的关键是通过代数式的变形,构造和式或积式为定值的式子,然后利用基本不等式求解最值.应用此种方法求解最值时,应把“1”的表达式与所求最值的表达式相乘求积或相除求商.
反思感悟
已知a>0,b>0,a+2b=1,求t= 的最小值.
跟踪训练1
因为a>0,b>0,a+2b=1,
消元法求最值
二
已知x>0,y>0,x+2y+2xy=8,求x+2y的最小值.
例2
所以x+2y的最小值为4.
延伸探究 已知x>0,y>0,满足xy=x+y+3,求xy的最小值.
所以xy的最小值为9.
含有多个变量的条件最值问题的解决方法
对含有多个变量的条件最值问题,若无法直接利用基本不等式求解,可尝试减少变量的个数,即用其中一个变量表示另一个,再代入代数式中转化为只含有一个变量的最值问题.
反思感悟
已知a>0,b>0,且2a+b=ab-1,则a+2b的最小值为________.
跟踪训练2
换元法求最值
三
已知x,y为正实数,且x+2y=4,则 的最小值为____.
例3
令x+2=a,2y+2=b,则a+b=8,
2
=1+ ≥2,当且仅当a=b=4时取等号,此时x=2,y=1.
故所求最小值为2.
换元法求最值的思路
观察已知与所求的结构特点,通过配凑系数,合理的变换新元,将问题转化为熟悉的模型,将问题明朗化,从而使问题得以解决.
反思感悟
已知a>0,b>0且a+b=3.式子 的最小值是___.
跟踪训练3
2
令a+2 020=x,b+2 021=y,
则x>2 020,y>2 021且x+y=4 044,
∴所求最小值为2.
课堂
小结
1.知识清单:
(1)常数代换法求最值.
(2)消元法求最值.
(3)换元法求最值.
2.方法归纳:常数代换法、消元法、换元法.
3.常见误区:一正、二定、三相等,常因缺少条件或符号导致错误.
随堂演练
1.y= (x>1)的最小值为
A.8 B.2 C.6 D.12
√
1
2
3
4
令t=x-1>0,∴x=t+1,
∴ymin=8.
1
2
3
4
2.已知x>0,y>0, =1,则使不等式x+y≥m恒成立的实数m的取值范
围是
A.m≥18 B.m≤18
C.m≥16 D.m≤16
√
即x=4,y=12时,等号成立,
又不等式x+y≥m恒成立,所以只需m≤16.
1
2
3
4
1
2
3
4
3.若正数x,y满足x2+xy-2=0,则3x+y的最小值是
A.4 B.2
C.2 D.4
√
因为x2+xy-2=0,
当且仅当x=1时等号成立.所以3x+y的最小值是4.
1
2
3
4
4.已知x,y为正实数,且x+y=2,则 的最小值为________.
1
2
3
4
∵x,y是正实数,且x+y=2,
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.若x>4,则y=
A.有最大值10 B.有最小值10
C.有最大值6 D.有最小值6
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为x>4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)已知a>0,b>0,a+b=1,对于代数式 ,下列说法正
确的是
A.最小值为9
B.最大值是9
C.当a=b= 时取得最小值
D.当a=b= 时取得最大值
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知a>0,b>0, ,若不等式2a+b≥9m恒成立,则m的最大值为
A.8 B.7 C.6 D.5
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴9m≤54,即m≤6.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为a>b>c,所以a-b>0,b-c>0,
当且仅当a-b=b-c时,等号成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵正数x,y满足x+4y-xy=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知a>0,b>0,则下列不等式中成立的是
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当且仅当a=b时,等号成立,B成立;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当且仅当a=b时,等号成立,C不成立;
当且仅当a=b时,等号成立,D成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.若a,b都是正数,且a+b=1,则(a+1)(b+1)的最大值是_____.
因为a,b都是正数,且a+b=1,
当且仅当a+1=b+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知t>0,则函数y= 的最小值为______.
当且仅当t=1时,等号成立.
故y的最小值为-2.
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知正数x,y满足x+2y=2.求 的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由于x+2y=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知a>0,b>0,a+3b=1.若m>a2+9b2+7ab恒成立,求实数m的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵a>0,b>0,a+3b=1,
∴a2+9b2+7ab=(a+3b)2+ab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设4x+y=a,x+y=b,
当a=2b,即2x=y时等号成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知x>0,y>0,且x+y=2,若4x+1-mxy≥0恒成立,则m的最大值为
A.6 B.4 C.8 D.2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为x+y=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设0A.9 B.
C.5 D.2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵00,
由基本不等式可得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.一家商店使用一架两臂不等长的天平秤黄金,一位顾客到店里购买10 g黄金,售货员先将5 g的砝码放在天平的左盘中,取出一些黄金放在天平右盘中使天平平衡;再将5 g的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次秤得的黄金交给顾客,你认为顾客购得的黄金是
A.大于10 g B.大于等于10 g
C.小于10 g D.小于等于10 g
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由于天平两臂不等长,
可设天平左臂长为a(a>0),右臂长为b(b>0),则a≠b,
再设先称得黄金为x g,后称得黄金为y g,
则bx=5a,ay=5b,
当且仅当 ,即a=b时等号成立,但a≠b,等号不成立,即x+y>10,
因此,顾客购得的黄金大于10 g.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由条件可得c=a2-3ab+4b2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
培优课 基本不等式的综合问题
第3章 不等式
基本不等式 (a,b≥0)在求最值中的应用广泛,方法
灵活多变,常见考查情形有常数代换法求最值、消元法求最值、换元法求最值等.
课时对点练
一、常数代换法求最值
二、消元法求最值
三、换元法求最值
随堂演练
内容索引
常数代换法求最值
一
例1
√
由x+y=1,得(x+2)+(y+1)=4,
常数代换法解题的关键是通过代数式的变形,构造和式或积式为定值的式子,然后利用基本不等式求解最值.应用此种方法求解最值时,应把“1”的表达式与所求最值的表达式相乘求积或相除求商.
反思感悟
已知a>0,b>0,a+2b=1,求t= 的最小值.
跟踪训练1
因为a>0,b>0,a+2b=1,
消元法求最值
二
已知x>0,y>0,x+2y+2xy=8,求x+2y的最小值.
例2
所以x+2y的最小值为4.
延伸探究 已知x>0,y>0,满足xy=x+y+3,求xy的最小值.
所以xy的最小值为9.
含有多个变量的条件最值问题的解决方法
对含有多个变量的条件最值问题,若无法直接利用基本不等式求解,可尝试减少变量的个数,即用其中一个变量表示另一个,再代入代数式中转化为只含有一个变量的最值问题.
反思感悟
已知a>0,b>0,且2a+b=ab-1,则a+2b的最小值为________.
跟踪训练2
换元法求最值
三
已知x,y为正实数,且x+2y=4,则 的最小值为____.
例3
令x+2=a,2y+2=b,则a+b=8,
2
=1+ ≥2,当且仅当a=b=4时取等号,此时x=2,y=1.
故所求最小值为2.
换元法求最值的思路
观察已知与所求的结构特点,通过配凑系数,合理的变换新元,将问题转化为熟悉的模型,将问题明朗化,从而使问题得以解决.
反思感悟
已知a>0,b>0且a+b=3.式子 的最小值是___.
跟踪训练3
2
令a+2 020=x,b+2 021=y,
则x>2 020,y>2 021且x+y=4 044,
∴所求最小值为2.
课堂
小结
1.知识清单:
(1)常数代换法求最值.
(2)消元法求最值.
(3)换元法求最值.
2.方法归纳:常数代换法、消元法、换元法.
3.常见误区:一正、二定、三相等,常因缺少条件或符号导致错误.
随堂演练
1.y= (x>1)的最小值为
A.8 B.2 C.6 D.12
√
1
2
3
4
令t=x-1>0,∴x=t+1,
∴ymin=8.
1
2
3
4
2.已知x>0,y>0, =1,则使不等式x+y≥m恒成立的实数m的取值范
围是
A.m≥18 B.m≤18
C.m≥16 D.m≤16
√
即x=4,y=12时,等号成立,
又不等式x+y≥m恒成立,所以只需m≤16.
1
2
3
4
1
2
3
4
3.若正数x,y满足x2+xy-2=0,则3x+y的最小值是
A.4 B.2
C.2 D.4
√
因为x2+xy-2=0,
当且仅当x=1时等号成立.所以3x+y的最小值是4.
1
2
3
4
4.已知x,y为正实数,且x+y=2,则 的最小值为________.
1
2
3
4
∵x,y是正实数,且x+y=2,
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1.若x>4,则y=
A.有最大值10 B.有最小值10
C.有最大值6 D.有最小值6
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为x>4,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)已知a>0,b>0,a+b=1,对于代数式 ,下列说法正
确的是
A.最小值为9
B.最大值是9
C.当a=b= 时取得最小值
D.当a=b= 时取得最大值
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知a>0,b>0, ,若不等式2a+b≥9m恒成立,则m的最大值为
A.8 B.7 C.6 D.5
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴9m≤54,即m≤6.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为a>b>c,所以a-b>0,b-c>0,
当且仅当a-b=b-c时,等号成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵正数x,y满足x+4y-xy=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知a>0,b>0,则下列不等式中成立的是
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当且仅当a=b时,等号成立,B成立;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当且仅当a=b时,等号成立,C不成立;
当且仅当a=b时,等号成立,D成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.若a,b都是正数,且a+b=1,则(a+1)(b+1)的最大值是_____.
因为a,b都是正数,且a+b=1,
当且仅当a+1=b+1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知t>0,则函数y= 的最小值为______.
当且仅当t=1时,等号成立.
故y的最小值为-2.
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知正数x,y满足x+2y=2.求 的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由于x+2y=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知a>0,b>0,a+3b=1.若m>a2+9b2+7ab恒成立,求实数m的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵a>0,b>0,a+3b=1,
∴a2+9b2+7ab=(a+3b)2+ab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设4x+y=a,x+y=b,
当a=2b,即2x=y时等号成立.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知x>0,y>0,且x+y=2,若4x+1-mxy≥0恒成立,则m的最大值为
A.6 B.4 C.8 D.2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为x+y=2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设0
C.5 D.2
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵0
由基本不等式可得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.一家商店使用一架两臂不等长的天平秤黄金,一位顾客到店里购买10 g黄金,售货员先将5 g的砝码放在天平的左盘中,取出一些黄金放在天平右盘中使天平平衡;再将5 g的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次秤得的黄金交给顾客,你认为顾客购得的黄金是
A.大于10 g B.大于等于10 g
C.小于10 g D.小于等于10 g
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由于天平两臂不等长,
可设天平左臂长为a(a>0),右臂长为b(b>0),则a≠b,
再设先称得黄金为x g,后称得黄金为y g,
则bx=5a,ay=5b,
当且仅当 ,即a=b时等号成立,但a≠b,等号不成立,即x+y>10,
因此,顾客购得的黄金大于10 g.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由条件可得c=a2-3ab+4b2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
