2022-2023学年沪科版七年级数学上册课件1.2数轴、相反数和绝对值(第3课时绝对值) 课件(共12张PPT)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学上册课件1.2数轴、相反数和绝对值(第3课时绝对值) 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
第1章 有理数
1.2 数轴、相反数、绝对值
第3课时 绝对值
学 习 目 标
2
1
3
会利用绝对值的定义求有理数的绝对值;(重点)
渗透数形结合、分类讨论的数学思想.(难点)
借助数轴理解绝对值的概念,并了解绝对值的几何意义;
温故知新
1、只有符号不同的两个数叫互为相反数。
2、数轴上表示相反数的两个对应点,分别位于原点两侧,且它们到原点的距离相等。
3、符号的化简:“数负号,偶正奇负”。
a–b的相反数是_b-a__。
若a与b互为相反数,则a+b=0_。
π有相反数吗?- π
知识讲解
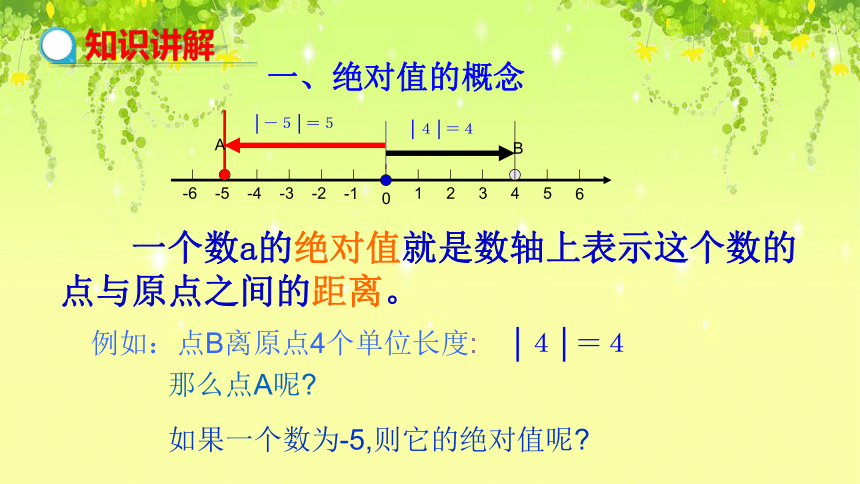
一、绝对值的概念
0
6
一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。
-1
-2
-3
-4
-5
-6
1
2
3
4
5
B
A
│-5│=5
│4│=4
例如:点B离原点4个单位长度:
│4│=4
那么点A呢
如果一个数为-5,则它的绝对值呢
知识讲解
例1 求下列各数的绝对值:
-21, +4/9, 0, -7.8 .
解:|-21|=21; |+4/9|=4/9;
|0|=0; |-7.8|=7.8 .
知识讲解
1、在数轴上标出到原点距离是6个单位长度的点,这样的点有几个?
2、求下列各数的绝对值.
| 30 |= |-30 |=
|+2.4|= |-2.4|=
| 15 |= |-15 |=
| 0 |=
练一练
知识讲解
想一想:
互为相反数的两个数的绝对值有什么关系?
相等
知识讲解
一个数的绝对值与这个数有什么关系
|a|=
a
-a
0
(a>0)
(a = 0)
(a < 0)
即
2、负数的绝对值是它的相反数; 如果a<0,那么|a|=-a;
3、0的绝对值是0.如果a=0,那么|a|=0
1、正数的绝对值是它本身; 如果a>0,那么 |a|=a;
二、绝对值的性质
随堂训练
一、基础训练
2、如果 |x| =8 ,求 x.
3、写出绝对值小于3.9的整数.
4、若 |m|=-m 则m是怎样的数?
1、求下列各数的绝对值.
(1)-38 (2)0.24
(3)a (a<0) (4) 3b(b<0)
8,-8
-3,-2,-1,0,1,2,3
非正数
二、尝试应用
随堂训练
1、下列说法正确的是 ( )
A、0是绝对值最小的数
B、绝对值较大的数较大
C、如果两个数的绝对值相等则这两个数一定相等
2、|x-3|+|y-2|=0成立的条件是( )
A、x=3
B、y=2
C、x=3 且y=2
A
C
1.一个数的绝对值是它本身,那么这个数一定是__________.
正数或零
4,3,2,1,0,-1,-2,-3,-4
2.绝对值小于5的整数有___个,分别
是——————————————————
9
三、拓展提高
随堂训练
3.已知:|a|=3,|b|=2 求a+b的值
解:5,-5,1,-1
1、绝对值 定义 :数轴上表示数a的点与原点的距离叫做数a的绝对值.记作 |a|.
2、绝对值 性质 : 正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0.
课堂小结
即
|a|=
a
-a
0
(a>0)
(a = 0)
(a < 0)
第1章 有理数
1.2 数轴、相反数、绝对值
第3课时 绝对值
学 习 目 标
2
1
3
会利用绝对值的定义求有理数的绝对值;(重点)
渗透数形结合、分类讨论的数学思想.(难点)
借助数轴理解绝对值的概念,并了解绝对值的几何意义;
温故知新
1、只有符号不同的两个数叫互为相反数。
2、数轴上表示相反数的两个对应点,分别位于原点两侧,且它们到原点的距离相等。
3、符号的化简:“数负号,偶正奇负”。
a–b的相反数是_b-a__。
若a与b互为相反数,则a+b=0_。
π有相反数吗?- π
知识讲解
一、绝对值的概念
0
6
一个数a的绝对值就是数轴上表示这个数的点与原点之间的距离。
-1
-2
-3
-4
-5
-6
1
2
3
4
5
B
A
│-5│=5
│4│=4
例如:点B离原点4个单位长度:
│4│=4
那么点A呢
如果一个数为-5,则它的绝对值呢
知识讲解
例1 求下列各数的绝对值:
-21, +4/9, 0, -7.8 .
解:|-21|=21; |+4/9|=4/9;
|0|=0; |-7.8|=7.8 .
知识讲解
1、在数轴上标出到原点距离是6个单位长度的点,这样的点有几个?
2、求下列各数的绝对值.
| 30 |= |-30 |=
|+2.4|= |-2.4|=
| 15 |= |-15 |=
| 0 |=
练一练
知识讲解
想一想:
互为相反数的两个数的绝对值有什么关系?
相等
知识讲解
一个数的绝对值与这个数有什么关系
|a|=
a
-a
0
(a>0)
(a = 0)
(a < 0)
即
2、负数的绝对值是它的相反数; 如果a<0,那么|a|=-a;
3、0的绝对值是0.如果a=0,那么|a|=0
1、正数的绝对值是它本身; 如果a>0,那么 |a|=a;
二、绝对值的性质
随堂训练
一、基础训练
2、如果 |x| =8 ,求 x.
3、写出绝对值小于3.9的整数.
4、若 |m|=-m 则m是怎样的数?
1、求下列各数的绝对值.
(1)-38 (2)0.24
(3)a (a<0) (4) 3b(b<0)
8,-8
-3,-2,-1,0,1,2,3
非正数
二、尝试应用
随堂训练
1、下列说法正确的是 ( )
A、0是绝对值最小的数
B、绝对值较大的数较大
C、如果两个数的绝对值相等则这两个数一定相等
2、|x-3|+|y-2|=0成立的条件是( )
A、x=3
B、y=2
C、x=3 且y=2
A
C
1.一个数的绝对值是它本身,那么这个数一定是__________.
正数或零
4,3,2,1,0,-1,-2,-3,-4
2.绝对值小于5的整数有___个,分别
是——————————————————
9
三、拓展提高
随堂训练
3.已知:|a|=3,|b|=2 求a+b的值
解:5,-5,1,-1
1、绝对值 定义 :数轴上表示数a的点与原点的距离叫做数a的绝对值.记作 |a|.
2、绝对值 性质 : 正数的绝对值是它本身;
负数的绝对值是它的相反数;
0 的绝对值是 0.
课堂小结
即
|a|=
a
-a
0
(a>0)
(a = 0)
(a < 0)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
