2.3 简谐振动的回复力与能量 人教版(2019)高中物理选择性必修一同步练习(含答案解析)
文档属性
| 名称 | 2.3 简谐振动的回复力与能量 人教版(2019)高中物理选择性必修一同步练习(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 449.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-16 00:00:00 | ||
图片预览


文档简介
2.3 简谐振动的回复力与能量人教版( 2019)高中物理选择性必修一同步练习
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共7小题,共28.0分)
如图所示,轻弹簧上端固定,下端悬吊一钢球,把钢球从平衡位置向下拉一段距离,由静止释放。以钢球平衡位置为坐标原点,竖直向上为正方向建立轴,当钢球在振动过程中某一次经过平衡位置时开始计时,钢球运动的位移时间图像如图所示。已知钢球振动过程中弹簧始终处于拉伸状态,则( )
A. 时刻钢球处于超重状态 B. 时刻钢球的速度方向向上
C. 时间内钢球的动能逐渐增大 D. 时间内钢球的机械能减小
如图所示,弹簧下面挂一质量为的物体,物体在竖直方向上做振幅为的简谐运动,当物体振动到最高点时,弹簧正好处于原长,弹簧在弹性限度内,则物体在振动过程中
A. 弹簧的弹性势能和物体动能总和不变
B. 物体在最低点时的加速度大小应为
C. 物体在最低点时所受弹簧的弹力大小应为
D. 弹簧的最大弹性势能等于
如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距。套在杆上的小球从中点以初速度向右运动,小球将做周期为的往复运动,则下列说法正确的是( )
A. 小球做简谐运动 B. 小球动能的变化周期为
C. 左端弹簧的弹性势能的变化周期为 D. 小球的运动周期与其初速度无关
光滑水平面上做简谐运动的弹簧振子的系统总能量表达式为,其中为弹簧的劲度系数,为简谐运动的振幅。若振子质量为,弹簧的劲度系数为。起振时系统具有势能和动能,则下列说法正确的是( )
A. 该振动的振幅为
B. 振子经过平衡位置时的速度为
C. 振子的最大加速度为
D. 若振子在位移最大处时,质量突变为,则振幅变大
甲、乙为竖直悬挂的两个弹簧振子,且悬挂振子的弹簧劲度系数相同,已知两球质量之比是,振动图像如图所示。则下列说法正确的是( )
A. 甲、乙两弹簧振子的振动频率之比是
B. 甲、乙两弹簧振子在内质点经过的路程之比是
C. 甲、乙两弹簧振子最大加速度之比是
D. 甲、乙两弹簧振子最大速度之比是
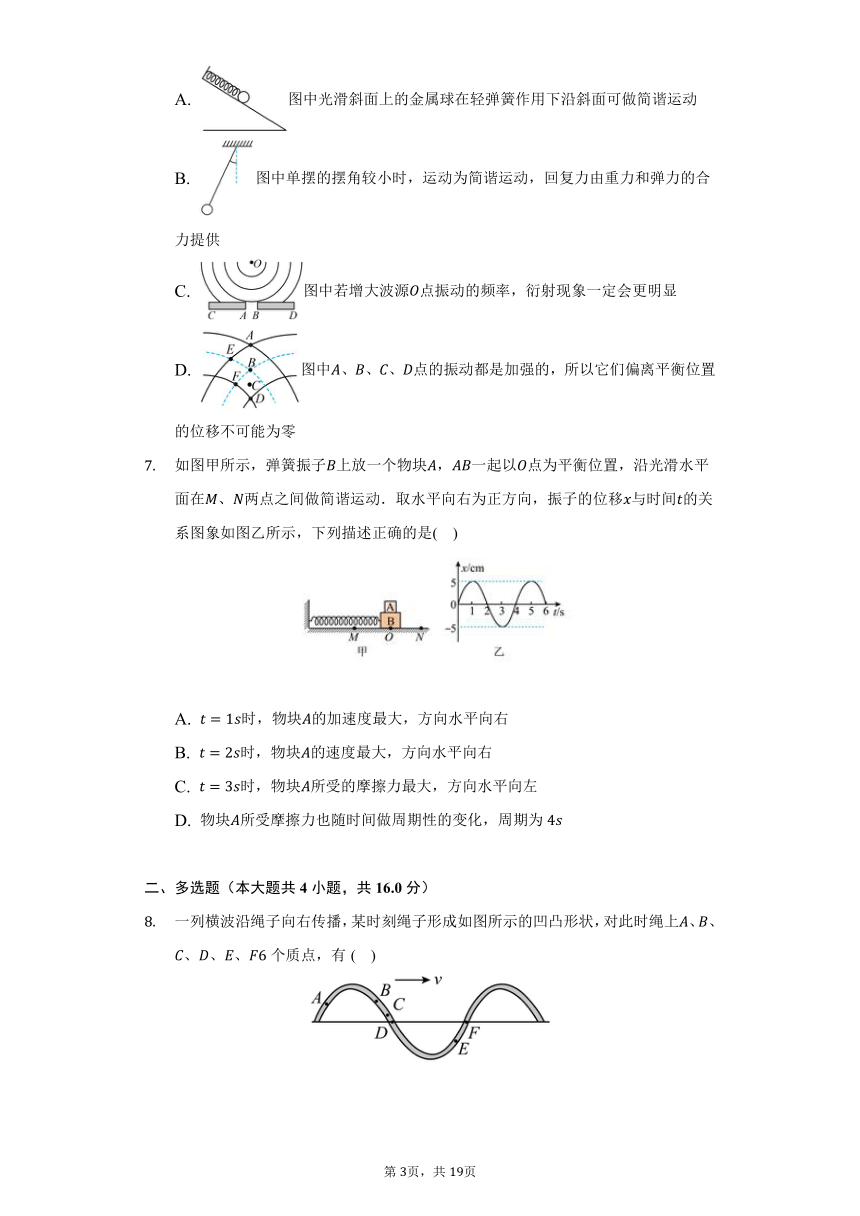
下列四幅图中关于机械振动和机械波的说法正确的是( )
A. 图中光滑斜面上的金属球在轻弹簧作用下沿斜面可做简谐运动
B. 图中单摆的摆角较小时,运动为简谐运动,回复力由重力和弹力的合力提供
C. 图中若增大波源点振动的频率,衍射现象一定会更明显
D. 图中、、、点的振动都是加强的,所以它们偏离平衡位置的位移不可能为零
如图甲所示,弹簧振子上放一个物块,一起以点为平衡位置,沿光滑水平面在、两点之间做简谐运动.取水平向右为正方向,振子的位移与时间的关系图象如图乙所示,下列描述正确的是( )
A. 时,物块的加速度最大,方向水平向右
B. 时,物块的速度最大,方向水平向右
C. 时,物块所受的摩擦力最大,方向水平向左
D. 物块所受摩擦力也随时间做周期性的变化,周期为
二、多选题(本大题共4小题,共16.0分)
一列横波沿绳子向右传播,某时刻绳子形成如图所示的凹凸形状,对此时绳上、、、、、个质点,有( )
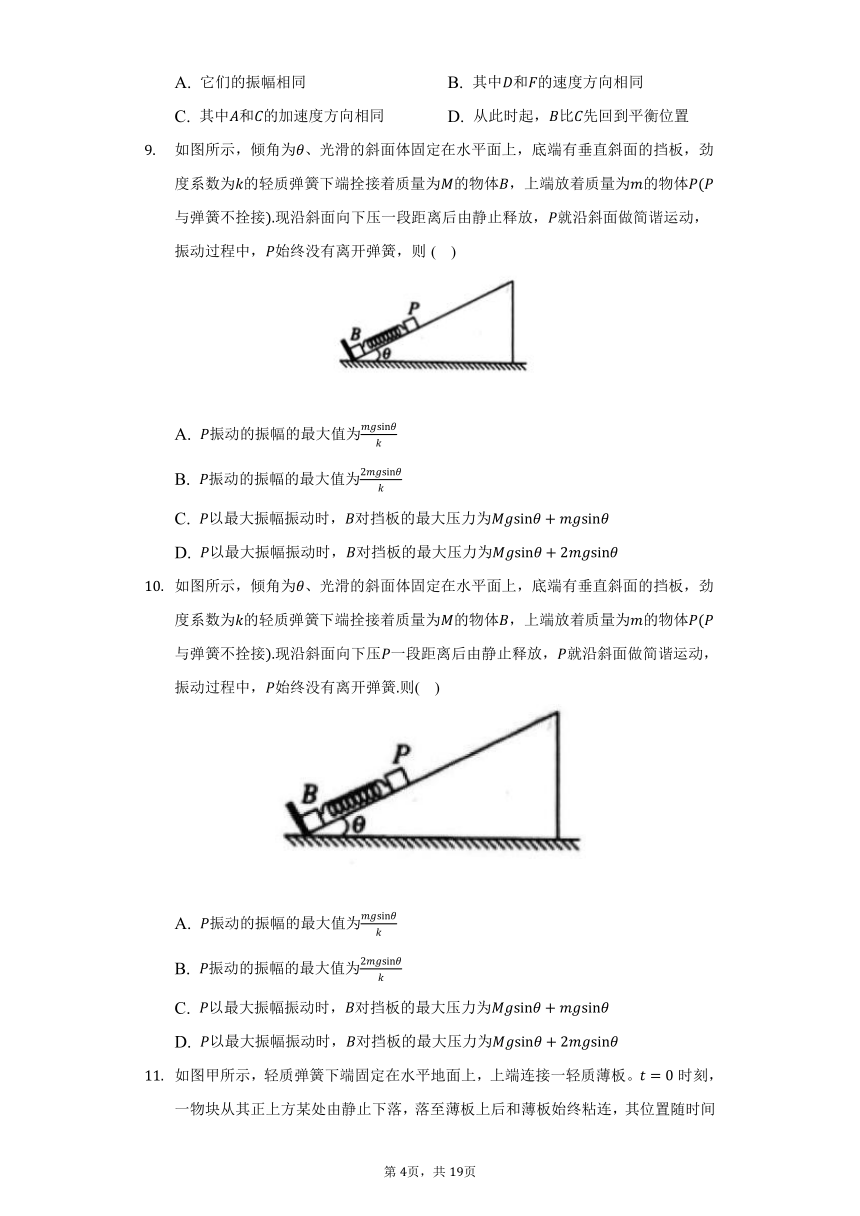
A. 它们的振幅相同 B. 其中和的速度方向相同
C. 其中和的加速度方向相同 D. 从此时起,比先回到平衡位置
如图所示,倾角为、光滑的斜面体固定在水平面上,底端有垂直斜面的挡板,劲度系数为的轻质弹簧下端拴接着质量为的物体,上端放着质量为的物体与弹簧不拴接现沿斜面向下压一段距离后由静止释放,就沿斜面做简谐运动,振动过程中,始终没有离开弹簧,则( )
A. 振动的振幅的最大值为
B. 振动的振幅的最大值为
C. 以最大振幅振动时,对挡板的最大压力为
D. 以最大振幅振动时,对挡板的最大压力为
如图所示,倾角为、光滑的斜面体固定在水平面上,底端有垂直斜面的挡板,劲度系数为的轻质弹簧下端拴接着质量为的物体,上端放着质量为的物体与弹簧不拴接现沿斜面向下压一段距离后由静止释放,就沿斜面做简谐运动,振动过程中,始终没有离开弹簧则( )
A. 振动的振幅的最大值为
B. 振动的振幅的最大值为
C. 以最大振幅振动时,对挡板的最大压力为
D. 以最大振幅振动时,对挡板的最大压力为
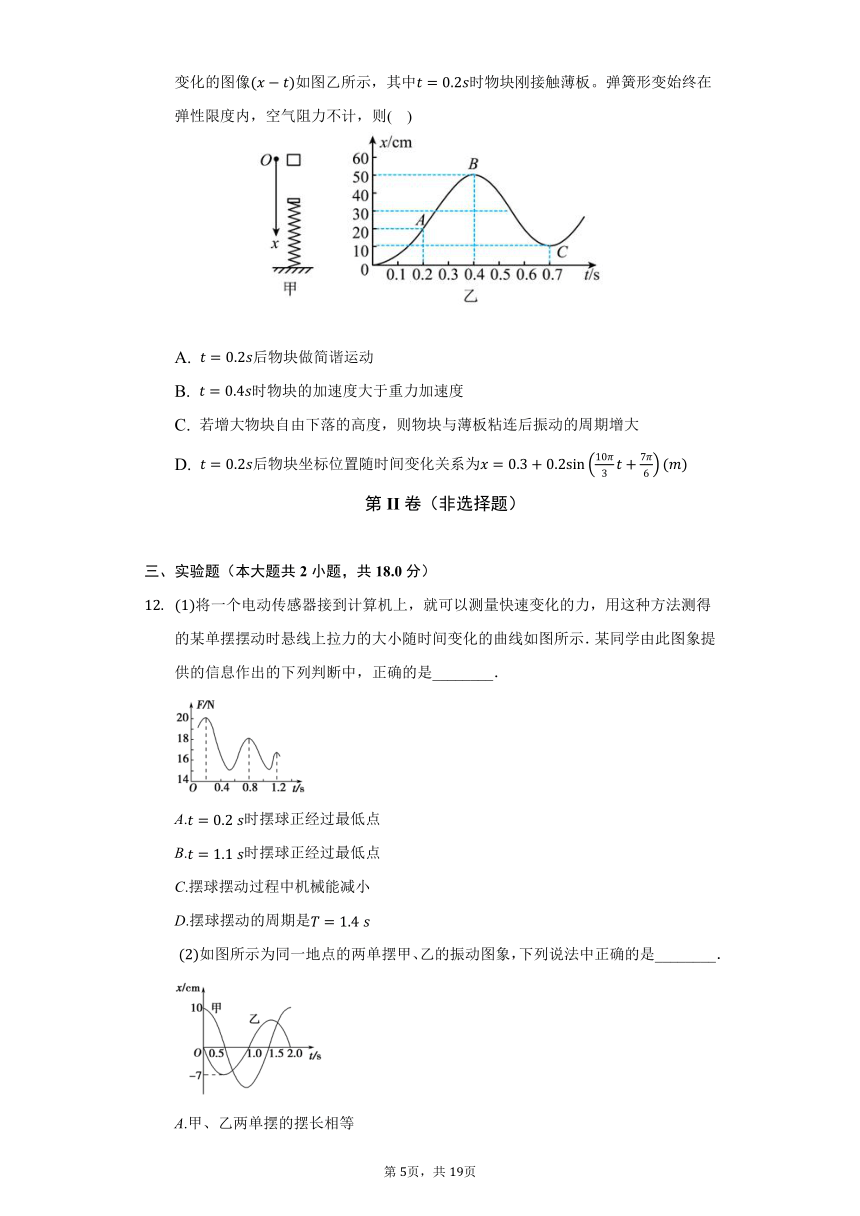
如图甲所示,轻质弹簧下端固定在水平地面上,上端连接一轻质薄板。时刻,一物块从其正上方某处由静止下落,落至薄板上后和薄板始终粘连,其位置随时间变化的图像如图乙所示,其中时物块刚接触薄板。弹簧形变始终在弹性限度内,空气阻力不计,则( )
A. 后物块做简谐运动
B. 时物块的加速度大于重力加速度
C. 若增大物块自由下落的高度,则物块与薄板粘连后振动的周期增大
D. 后物块坐标位置随时间变化关系为
第II卷(非选择题)
三、实验题(本大题共2小题,共18.0分)
将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示.某同学由此图象提供的信息作出的下列判断中,正确的是________.
A.时摆球正经过最低点
B.时摆球正经过最低点
C.摆球摆动过程中机械能减小
D.摆球摆动的周期是
如图所示为同一地点的两单摆甲、乙的振动图象,下列说法中正确的是________.
A.甲、乙两单摆的摆长相等
B.甲摆的振幅比乙摆大
C.甲摆的机械能比乙摆大
D.在时有正向最大加速度的是乙摆
根据水平弹簧振子图,可分析各个物理量的变化关系如下,填写表格中个空位:
振子的运动
位移 方向 向右 向左 向左 向右
大小 减小 减小 增大
回复力 方向 向右 向右 向左
大小 增大 减小 增大
加速度 方向 向左 向右 向右
大小 减小 增大 减小
速度 方向 向左 向左 向右 向右
大小 增大 减小 增大 减小
振子的动能 增大 减小 增大 减小
弹簧的势能 减小 增大 增大
系统总能量 不变 不变 不变 不变
质点在外力作用下沿竖直方向做简谐运动,带动、、各个质点依次上下运动,把振动从绳左端传到右端,已知时质点开始向上振动,时质点到达上方最大位移处,质点开始向上运动,时,质点振动方向______,质点的振动方向_______填“向上”“向下”“向左”或“向右”。
如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
实验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量________填选项前的符号,间接地解决这个问题.
A.小球开始释放高度
B.小球抛出点距地面的高度
C.小球做平抛运动的射程
图中点是小球抛出点在地面上的垂直投影,实验时先让入射球多次从斜轨上位置静止释放,找到其平均落地点的位置,测量平抛射程,然后,把被碰小球静置于轨道的水平部分,再将入射球从斜轨上位置静止释放,与小球相碰,并多次重复.
接下来要完成的必要步骤是________填选项前的符号
A.用天平测量两个小球的质量、
B.测量小球开始释放高度
C.测量抛出点距地面的高度
D.分别找到、相碰后平均落地点的位置、
E.测量平抛射程、
若两球相碰前后的动量守恒,其表达式可表示为______________用中测量的量表示;
若碰撞是弹性碰撞,那么还应满足的表达式为________________用中测量的量表示.
四、计算题(本大题共3小题,共30.0分)
如图所示,倾角为的斜面体斜面光滑且足够长固定在水平地面上,斜面顶端与劲度系数为、自然长度为的轻质弹簧相连,弹簧的另一端连接着质量为的物块.压缩弹簧使其长度为时将物块由静止开始释放物块做简谐运动,重力加速度为.
求物块处于平衡位置时弹簧的长度;
物块做简谐运动的振幅是多少;
选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标系,用表示物块相对于平衡位置的位移,证明物块做简谐运动.已知做简谐运动的物体所受的回复力满足
将一测力传感器连接到计算机上就可以测量快速变化的力。图甲中点为单摆的固定悬点,现将小摆球可视为质点拉至点,此时细线处于张紧状态,释放摆球,则摆球将在竖直平面内的、、之间来回摆动,其中点为运动中的最低位置,,小于且是未知量。图乙表示由计算机得到的小球对摆线的拉力大小随时间变化的曲线,且图中时刻为摆球从点开始运动的时刻。试根据力学规律和题中包括图中所给的信息求:取
单摆的振动周期和摆长;
摆球的质量;
摆球运动过程中的最大速度。
弹簧振子以点为平衡位置,在、两点间做简谐运动,在时刻,振子从、间的点以速度向点运动;在时,振子速度第一次变为;在时,振子速度第二次变为,已知、之间的距离为.
求弹簧振子的振幅;
求弹簧振子振动周期和频率;
求振子在内通过的路程及末的位移大小.
答案和解析
1.【答案】
【解析】解:、时刻,钢球位于平衡位置上方,位移为正,所以加速度为负,有向下的加速度,处于失重状态,故错误;
、时刻,钢球位于平衡位置下方,正在远离平衡位置,速度方向向下,故错误;
、时间内,钢球的速度先增大后减小,动能先增大后减小,故错误;
、时间内,钢球克服弹力做功,根据能量守恒定律可知,钢球的机械能减小,故正确。
故选:。
分析钢球的位移方向,从而找到其加速度方向,再根据超重和失重条件进行分析;
根据图像分析钢球的运动方向;
衡位置钢球的速度增大,远离平衡位置钢球的速度减小;
分析钢球的做功情况,从而分析出钢球的机械能变化情况。
解决该题的关键是知道简谐运动的加速度与位移方向相反,掌握简谐运动的速度变化情况,掌握机械能守恒条件。
2.【答案】
【解析】
【分析】
只有重力和弹力做功,系统机械能守恒,弹簧的弹性势能、物体的动能、重力势能之和不变;在最低点弹性势能最大,根据能量守恒定律,求出最低点的弹性势能.
解决本题的关键抓住简谐运动的对称性以及灵活运用能量守恒定律和机械能守恒定律.
【解答】
A.在运动的过程中,只有重力和弹力做功,系统机械能守恒,弹簧的弹性势能、物体的动能、重力势能之和不变。弹簧的弹性势能是变化的,故物体的重力势能和物体动能总和是变化的,故A错误;
小球在简谐运动的平衡位置处,,所以在最低点时,形变量为,弹力大小为。加速度大小为,故BC错误;
D.从最高点到最低点,动能变化为,重力势能减小,则弹性势能增加而初位置弹性势能为,在最低点弹性势能最大,为故D正确。
故选D。
3.【答案】
【解析】
【分析】
根据简谐运动的特点分析出小球的运动是否属于简谐运动;
分析出小球压缩弹簧过程中的受力特点和速度变化特点,由此完成分析;
分阶段分析出小球在匀速阶段的时间和与弹簧作用阶段的时间与速度的关系,最后完成分析。
本题主要考查了简谐运动的相关应用,理解简谐运动的回复力和位移的关系,同时熟记简谐运动的周期公式即可完成解答。
【解答】
A.物体做简谐运动的条件是在运动过程中所受回复力与位移成正比,且方向始终指向平衡位置,可知小球在杆中点到接触弹簧过程中,所受合力为零,故小球不是做简谐运动,故A错误;
假设杆中点为,小球向右压缩弹簧至最大压缩量时的位置为,小球向左压缩弹簧至最大压缩量时的位置为,可知小球做周期为的往复运动,运动过程为,根据对称性可知小球从与,这两个过程的动能变化完全一致,两根弹簧的总弹性势能的变化完全一致,故小球动能的变化周期为,两根弹簧的总弹性势能的变化周期为,其中一根弹簧的弹性势能变化的周期为,故B错误,C正确;
D.小球的初速度为时,可知小球在匀速阶段的时间变为原来的倍,接触弹簧过程,根据弹簧振子的周期公式可知,接触弹簧过程中所用时间与速度无关,故D错误。
故选C。
4.【答案】
【解析】
【分析】
本题考查弹簧振子,振动系统的机械能守恒,即动能与弹性势能之和守恒,根据最大位移处求,根据平衡位置处求速度。
最大位移处加速度最大,根据牛顿第二定律求解加速度。
【解答】
A、根据题意,系统具有总能量,因为弹簧振子在光滑水平面上做简谐振动,弹簧的最大伸长量等于振幅,有,
解得,故A错误;
B、振子经过平衡位置时,弹簧伸长量为零,弹性势能为零,振子经过平衡位置时的动能,根据,解得,故B错误;
C、弹簧的最大加速度大小为,故C正确;
D、振子在最大位移处时系统只有弹性势能,质量突变为,振动系统的总能量不变,振幅不变,故D错误。
故选C。
5.【答案】
【解析】
【分析】
本题结合弹簧振子的振动图像考查弹簧振子的振动规律。解决问题的关键是能从振动图像读取有关信息,比如周期,振幅,熟悉描述振动的物理量之间的关系。
【解答】
从图中直接可以看出甲的振幅为,乙的振幅,甲的周期,乙的周期。
、甲、乙两弹簧振子的振动周期之比为,根据,两者的频率之比为,故错误;
、甲振动了个周期,路程为,乙振动了个周期,路程为,故路程之比为,故正确;
、根据胡克定律可知,甲、乙的最大回复力之比为,又因为两球质量之比是,根据牛顿第二定律可知,甲、乙两弹簧振子最大加速度之比是,故错误;
、经分析,当到达平衡位置时,速度最大,设此时最大速度为,甲弹簧振子的弹簧伸长量为,在最低点时的弹簧伸长量为,则有: ,从最低点到平衡位置时,根据动能定理得: ,又因为 ,联立解得,所以最大速度之比为,故错误。
6.【答案】
【解析】
【分析】
用简谐运动的条件和机械波的特点分析;
根据单摆运动的特点进行分析;
当孔、缝的宽度与波长差不多或者比波长小时,就能够发生明显的衍射现象,这是发生明显衍射的条件;
频率相同的两列水波的叠加:当波峰与波峰、波谷与波谷相遇时振动是加强的;当波峰与波谷相遇时振动是减弱的。
【解答】
、光滑斜面上的金属球做简谐运动,回复力由弹簧弹力与重力沿斜面方向的分力的合力提供,故正确;
、单摆的摆角较小时,运动为简谐运动,回复力由重力沿切线方向的分力提供,故错误;
、若增大波源点振动的频率,由可知波长变短,衍射现象会更不明显,故错误;
、点和点是波峰与波峰、点是波谷与波谷相遇的点,都是振动加强的点,在它们连线上的点也是振动加强点,它们的振幅最大,但是在振动过程中位移会不断变化,当他们振动到平衡位置时,位移为零,故错误。
7.【答案】
【解析】
【分析】
根据弹簧振子的图象,当振子在平衡位置时速度最大,加速度为零;当偏离平衡位置距离最大时,速度为零,加速度最大;其中加速度方向始终指向平衡位置,速度方向看下一时刻的运动情况即可判断。
本题考查了弹簧振子的简谐振动图象,解题的关键是把握住振动图象中,速度、加速度的大小与方向的判断,有一定规律性,平时注意积累。
【解答】
A.时,物块处于振幅最大处,方向指向平衡位置,因此加速度最大且方向为负方向,水平向左,故A错误;
B.时,物块处于平衡位置,速度最大,下一时刻向下运动,速度方向为负方向,水平向左,故B错误;
C.时,物块处于负向振幅最大处,方向指向平衡位置,因此加速度最大且方向为正方向,水平向右,加速度大小相同,方向相同,故物块加速度最大,所受的摩擦力最大,方向水平向右,故C错误;
D.一起以点为平衡位置,沿光滑水平面在、两点之间做简谐运动,周期为,故物块所受回复力即摩擦力也随时间做周期性的变化,周期为,故D正确。
8.【答案】
【解析】
【分析】
该题考查波的图像相关知识。不考虑能量损耗,各质点振幅相同;根据“带动法”分析速度方向;根据回复力分析加速度方向;根据质点振动情况分析谁先到达平衡位置。
【解答】
A.各质点均做受迫振动,不考虑能量损耗,各质点振幅相同,故A正确;
B.根据“带动法”可知,此时速度方向向上,速度方向向下,故B错误;
C.和两质点均在平衡位置上方,回复力均向下,加速度方向均向下,故C正确;
D.此时和两质点都向上运动,比先到达最大位移处,先回到平衡位置,故D正确。
故选ACD。
9.【答案】
【解析】
【分析】
结合受力分析,确定的平衡位置,然后结合题目的条件即可求出振幅最大值;当运动至最低点时,弹簧的压缩量最大,结合受力情况即可求解对挡板的最大压力。
该题考查简谐振动的受力问题,掌握简谐运动的特点即可解答。
【解答】
若做简谐振动,则位于平衡位置时,沿斜面方向受到的合外力等于,而沿斜面的方向上有重力的分力和弹簧的弹力,可知二者大小相等,方向相反,即,所以,由题意,向上到达的最高点的位置时,弹簧的长度恰好等于原长是仍然能做简谐振动的最高点,所以的最大振幅,,故A正确,B错误;
以增大振幅振动时,由简谐振动的特点可知到达最低点时,弹簧的压缩量;以为研究对象,则受到重力、斜面的支持力、挡板的支持力和弹簧沿斜面向下的压力,沿斜面的方向,联立得,由牛顿第三定律可知以最大振幅振动时,对挡板的最大压力为,故C错误,D正确。
10.【答案】
【解析】
【分析】
结合受力分析,确定的平衡位置,然后结合题目的条件即可求出振幅最大值;当运动至最低点时,弹簧的压缩量最大,结合受力情况即可求解对挡板的最大压力。
该题考查简谐振动的受力问题,掌握简谐运动的特点即可解答。
【解答】
若做简谐振动,则位于平衡位置时,沿斜面方向受到的合外力等于,而沿斜面的方向上有重力的分力和弹簧的弹力,可知二者大小相等,方向相反,即,所以,由题意,向上到达的最高点的位置时,弹簧的长度恰好等于原长是仍然能做简谐振动的最高点,所以的最大振幅,,故A正确,B错误;
以增大振幅振动时,由简谐振动的特点可知到达最低点时,弹簧的压缩量;以为研究对象,则受到重力、斜面的支持力、挡板的支持力和弹簧沿斜面向下的压力,沿斜面的方向,联立得,由牛顿第三定律可知以最大振幅振动时,对挡板的最大压力为,故C错误,D正确。
11.【答案】
【解析】解:时物块刚接触薄板,落至薄板上后和薄板始终粘连,构成竖直方向的弹簧振子,并且从图像看,以后的图像为正弦函数曲线,故A正确;
B.薄板为轻质薄板,质量可忽略不计。由图乙可知,点是图像的最高点,点是图像最低点,根据简谐运动的对称性可知,最高点的加速度和最低点的加速度大小相等,即,由简谐运动的加速度满足
可知,与成正比,设点处的偏离平衡位置位移大小为,点处偏离平衡位置的位移大小为,有,所以,故,到点时,物块只受重力,,所以,故B正确;
C.弹簧振子的周期只与震动系统本身有关,与物块起始下落的高度无关,故物块与薄板粘连后震动周期不变,故C错误;
D.由图乙可知,
振幅为,后物块位置随时间变化关系式为
当时,,代入上式得
所以
故D正确。
故选:。
物块与薄板一起运动时是简谐运动,根据简谐运动的对称性确定物块的加速度;分析运动过程中物块的受力情况,根据牛顿第二定律分析加速度的变化;根据简谐运动的角速度,振幅可解得位置随时间的表达式。
解决本题的关键是要分析清楚物块的运动过程和受力情况,掌握简谐运动的对称性,来分析物块所受合外力的变化情况,掌握简谐运动的特点。
12.【答案】
【解析】
【分析】
摆球在摆动的过程中,在最低点时拉力最大,根据牛顿第二定律分析拉力与速度的关系,从而判断出机械能的变化.摆球在摆动的过程中,一个周期内两次经过最低点。
由图读出两单摆的周期,由单摆的周期公式分析摆长关系;由位移的最大值读出振幅;由于两摆的质量未知,无法比较机械能的大小;根据加速度与位移方向相反,确定加速度的方向。
【解答】
摆球经过最低点时,拉力最大,由图知在时,拉力最大,所以此时摆球经过最低点;在时,摆球的拉力最小,不是经过最低点,故A正确,B错误;
C.在最低点,根据牛顿第二定律得:,则在最低点的拉力减小,可知小球的速度减小,机械能减小,故C正确;
D.在一个周期内摆球两次经过最低点,根据图象知周期故D错误;
故选AC。
由图看出,两单摆的周期相同,同一地点相同,由单摆的周期公式得知,甲、乙两单摆的摆长相等.故A正确;
B.甲摆的振幅为,乙摆的振幅为,则甲摆的振幅比乙摆大.故B正确;
C.尽管甲摆的振幅比乙摆大,两摆的摆长也相等,但由于两摆的质量未知,无法比较机械能的大小.故C错误;
D.在时,甲摆经过平衡位置,振动的加速度为零,而乙摆的位移为负的最大,则乙摆具有正向最大加速度.故D正确;
故选ABD。
13.【答案】
振子的运动
位移 方向 向右 向左 向左 向右
大小 减小 增大 减小 增大
回复力 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
加速度 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
速度 方向 向左 向左 向右 向右
大小 增大 减小 增大 减小
振子的动能 增大 减小 增大 减小
弹簧的势能 减小 增大 减小 增大
系统总能量 不变 不变 不变 不变
向下向下
【解析】根据简谐振动规律解答即可,点为平衡位置,可判断位移的方向和大小的变化,回复力总是指向平衡位置,衡位置回复力减小,远离平衡位置回复力增大,根据牛顿第二定律,加速度的变化与回复力的变化时一致的,动能与弹性势能相互转化,衡位置弹性势能减小,动能增大,远离则反之。所以答案分别为增大、向右、减小、向左、增大、减小。
根据题意可知时质点开始向上振动,时,质点振动了,则其振动方向向下;振动从质点传播到质点经过,则质点到质点的距离为,所以则点到质点之间的距离为,波从质点传播到质点的时间为,故时,质点振动了,正向下振动。
小球碰前和碰后的速度都用平抛运动来测定,即而由知,每次竖直高度相等,平抛时间相等.即;则可得故只需测量射程,因而选C.
由表达式知:在已知时,需测量、、和,故必要步骤、、.
若为弹性碰撞,同时还满足机械能守恒.
14.【答案】解:物体平衡时,受重力、支持力和弹簧的弹力,根据平衡条件,有:
解得:
故弹簧的长度为;
物体做简谐运动的振幅为:
;
物体到达平衡位置下方位置时,弹力为:;
故合力为:;
故物体做简谐运动;
答:物块处于平衡位置时弹簧的长度为;
物块做简谐运动的振幅是;
证明如上.
【解析】物体平衡时,受重力、支持力和弹簧的弹力,三力平衡,根据平衡条件并结合正交分解法和胡克定律列式求解;
物块做简谐运动的振幅等于物体处于平衡位置时弹簧的伸长量与开始的压缩量的和;
简谐运动中,合力充当回复力,满足条件.
本题关键是对滑块受力分析,利用简谐运动的对称性求解弹簧最大伸长量,明确简谐运动的条件是回复力满足:.
15.【答案】解:小球在一个周期内两次经过最低点,根据该规律,则小球的周期:
由单摆的周期公式为:
解得:
摆球在点和点受力分析如图所示:
在最高点,有:
在最低点设小球的速度为,有:
从到,机械能守恒,由机械能守恒定律得:
联立三式并代入数据得:,
由知,摆球运动过程中的最大速度。
【解析】小球运动到最低点时,绳子的拉力最大,在一个周期内两次经过最低点,根据该规律,求出单摆的周期.再根据单摆的周期公式求出摆长;
小球在最高点时绳子的拉力最小,在最低点时绳子拉力最大,求出最高点和最低点绳子拉力的表达式,再结合动能定理或机械能守恒定律求出摆球的质量;
根据最低点时绳子的拉力最大,结合牛顿第二定律求出摆球的最大速度。
本题考查了单摆周期公式的应用,解决本题的关键掌握单摆的运动规律,知道单摆的周期公式,以及会灵活运用机械能守恒定律、牛顿第二定律解题。
16.【答案】解:弹簧振子以点为平衡位置,在、两点间做简谐运动,所以振幅是之间距离而,所以
由简谐运动的对称性可知到的时间与返回的时间是相等的,所以:;
同时由简谐振动的对称性可知:
又由于:
联立得:
所以:
内路程:
由的分析可知,从时刻,经过时间振子到达点;所以在时刻质点又一次到达点,所以质点的位移是。
答:弹簧振子的振幅是;
弹簧振子振动周期是,频率是;
振子在内通过的路程是;末的位移大小是。
【解析】本题在于关键分析质点的振动情况,确定点的运动方向和周期.写振动方程时要抓住三要素:振幅、角频率和初相位。
由、之间的距离得出振幅;
在时刻,振子从间的点以速度向点运动,经过它的速度大小第一次与相同,方向相反,再经过它的速度大小第二次与相同,方向与原来相反,质点运动到关于平衡位置对称的位置,求出周期。
由、之间的距离得出振幅,结合振子开始计时的位置,求出振子在内通过的路程;结合振子开始计时的位置然后求出末的位移大小。
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共7小题,共28.0分)
如图所示,轻弹簧上端固定,下端悬吊一钢球,把钢球从平衡位置向下拉一段距离,由静止释放。以钢球平衡位置为坐标原点,竖直向上为正方向建立轴,当钢球在振动过程中某一次经过平衡位置时开始计时,钢球运动的位移时间图像如图所示。已知钢球振动过程中弹簧始终处于拉伸状态,则( )
A. 时刻钢球处于超重状态 B. 时刻钢球的速度方向向上
C. 时间内钢球的动能逐渐增大 D. 时间内钢球的机械能减小
如图所示,弹簧下面挂一质量为的物体,物体在竖直方向上做振幅为的简谐运动,当物体振动到最高点时,弹簧正好处于原长,弹簧在弹性限度内,则物体在振动过程中
A. 弹簧的弹性势能和物体动能总和不变
B. 物体在最低点时的加速度大小应为
C. 物体在最低点时所受弹簧的弹力大小应为
D. 弹簧的最大弹性势能等于
如图所示,一根固定在墙上的水平光滑杆,两端分别固定着相同的轻弹簧,两弹簧自由端相距。套在杆上的小球从中点以初速度向右运动,小球将做周期为的往复运动,则下列说法正确的是( )
A. 小球做简谐运动 B. 小球动能的变化周期为
C. 左端弹簧的弹性势能的变化周期为 D. 小球的运动周期与其初速度无关
光滑水平面上做简谐运动的弹簧振子的系统总能量表达式为,其中为弹簧的劲度系数,为简谐运动的振幅。若振子质量为,弹簧的劲度系数为。起振时系统具有势能和动能,则下列说法正确的是( )
A. 该振动的振幅为
B. 振子经过平衡位置时的速度为
C. 振子的最大加速度为
D. 若振子在位移最大处时,质量突变为,则振幅变大
甲、乙为竖直悬挂的两个弹簧振子,且悬挂振子的弹簧劲度系数相同,已知两球质量之比是,振动图像如图所示。则下列说法正确的是( )
A. 甲、乙两弹簧振子的振动频率之比是
B. 甲、乙两弹簧振子在内质点经过的路程之比是
C. 甲、乙两弹簧振子最大加速度之比是
D. 甲、乙两弹簧振子最大速度之比是
下列四幅图中关于机械振动和机械波的说法正确的是( )
A. 图中光滑斜面上的金属球在轻弹簧作用下沿斜面可做简谐运动
B. 图中单摆的摆角较小时,运动为简谐运动,回复力由重力和弹力的合力提供
C. 图中若增大波源点振动的频率,衍射现象一定会更明显
D. 图中、、、点的振动都是加强的,所以它们偏离平衡位置的位移不可能为零
如图甲所示,弹簧振子上放一个物块,一起以点为平衡位置,沿光滑水平面在、两点之间做简谐运动.取水平向右为正方向,振子的位移与时间的关系图象如图乙所示,下列描述正确的是( )
A. 时,物块的加速度最大,方向水平向右
B. 时,物块的速度最大,方向水平向右
C. 时,物块所受的摩擦力最大,方向水平向左
D. 物块所受摩擦力也随时间做周期性的变化,周期为
二、多选题(本大题共4小题,共16.0分)
一列横波沿绳子向右传播,某时刻绳子形成如图所示的凹凸形状,对此时绳上、、、、、个质点,有( )
A. 它们的振幅相同 B. 其中和的速度方向相同
C. 其中和的加速度方向相同 D. 从此时起,比先回到平衡位置
如图所示,倾角为、光滑的斜面体固定在水平面上,底端有垂直斜面的挡板,劲度系数为的轻质弹簧下端拴接着质量为的物体,上端放着质量为的物体与弹簧不拴接现沿斜面向下压一段距离后由静止释放,就沿斜面做简谐运动,振动过程中,始终没有离开弹簧,则( )
A. 振动的振幅的最大值为
B. 振动的振幅的最大值为
C. 以最大振幅振动时,对挡板的最大压力为
D. 以最大振幅振动时,对挡板的最大压力为
如图所示,倾角为、光滑的斜面体固定在水平面上,底端有垂直斜面的挡板,劲度系数为的轻质弹簧下端拴接着质量为的物体,上端放着质量为的物体与弹簧不拴接现沿斜面向下压一段距离后由静止释放,就沿斜面做简谐运动,振动过程中,始终没有离开弹簧则( )
A. 振动的振幅的最大值为
B. 振动的振幅的最大值为
C. 以最大振幅振动时,对挡板的最大压力为
D. 以最大振幅振动时,对挡板的最大压力为
如图甲所示,轻质弹簧下端固定在水平地面上,上端连接一轻质薄板。时刻,一物块从其正上方某处由静止下落,落至薄板上后和薄板始终粘连,其位置随时间变化的图像如图乙所示,其中时物块刚接触薄板。弹簧形变始终在弹性限度内,空气阻力不计,则( )
A. 后物块做简谐运动
B. 时物块的加速度大于重力加速度
C. 若增大物块自由下落的高度,则物块与薄板粘连后振动的周期增大
D. 后物块坐标位置随时间变化关系为
第II卷(非选择题)
三、实验题(本大题共2小题,共18.0分)
将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示.某同学由此图象提供的信息作出的下列判断中,正确的是________.
A.时摆球正经过最低点
B.时摆球正经过最低点
C.摆球摆动过程中机械能减小
D.摆球摆动的周期是
如图所示为同一地点的两单摆甲、乙的振动图象,下列说法中正确的是________.
A.甲、乙两单摆的摆长相等
B.甲摆的振幅比乙摆大
C.甲摆的机械能比乙摆大
D.在时有正向最大加速度的是乙摆
根据水平弹簧振子图,可分析各个物理量的变化关系如下,填写表格中个空位:
振子的运动
位移 方向 向右 向左 向左 向右
大小 减小 减小 增大
回复力 方向 向右 向右 向左
大小 增大 减小 增大
加速度 方向 向左 向右 向右
大小 减小 增大 减小
速度 方向 向左 向左 向右 向右
大小 增大 减小 增大 减小
振子的动能 增大 减小 增大 减小
弹簧的势能 减小 增大 增大
系统总能量 不变 不变 不变 不变
质点在外力作用下沿竖直方向做简谐运动,带动、、各个质点依次上下运动,把振动从绳左端传到右端,已知时质点开始向上振动,时质点到达上方最大位移处,质点开始向上运动,时,质点振动方向______,质点的振动方向_______填“向上”“向下”“向左”或“向右”。
如图,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
实验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量________填选项前的符号,间接地解决这个问题.
A.小球开始释放高度
B.小球抛出点距地面的高度
C.小球做平抛运动的射程
图中点是小球抛出点在地面上的垂直投影,实验时先让入射球多次从斜轨上位置静止释放,找到其平均落地点的位置,测量平抛射程,然后,把被碰小球静置于轨道的水平部分,再将入射球从斜轨上位置静止释放,与小球相碰,并多次重复.
接下来要完成的必要步骤是________填选项前的符号
A.用天平测量两个小球的质量、
B.测量小球开始释放高度
C.测量抛出点距地面的高度
D.分别找到、相碰后平均落地点的位置、
E.测量平抛射程、
若两球相碰前后的动量守恒,其表达式可表示为______________用中测量的量表示;
若碰撞是弹性碰撞,那么还应满足的表达式为________________用中测量的量表示.
四、计算题(本大题共3小题,共30.0分)
如图所示,倾角为的斜面体斜面光滑且足够长固定在水平地面上,斜面顶端与劲度系数为、自然长度为的轻质弹簧相连,弹簧的另一端连接着质量为的物块.压缩弹簧使其长度为时将物块由静止开始释放物块做简谐运动,重力加速度为.
求物块处于平衡位置时弹簧的长度;
物块做简谐运动的振幅是多少;
选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标系,用表示物块相对于平衡位置的位移,证明物块做简谐运动.已知做简谐运动的物体所受的回复力满足
将一测力传感器连接到计算机上就可以测量快速变化的力。图甲中点为单摆的固定悬点,现将小摆球可视为质点拉至点,此时细线处于张紧状态,释放摆球,则摆球将在竖直平面内的、、之间来回摆动,其中点为运动中的最低位置,,小于且是未知量。图乙表示由计算机得到的小球对摆线的拉力大小随时间变化的曲线,且图中时刻为摆球从点开始运动的时刻。试根据力学规律和题中包括图中所给的信息求:取
单摆的振动周期和摆长;
摆球的质量;
摆球运动过程中的最大速度。
弹簧振子以点为平衡位置,在、两点间做简谐运动,在时刻,振子从、间的点以速度向点运动;在时,振子速度第一次变为;在时,振子速度第二次变为,已知、之间的距离为.
求弹簧振子的振幅;
求弹簧振子振动周期和频率;
求振子在内通过的路程及末的位移大小.
答案和解析
1.【答案】
【解析】解:、时刻,钢球位于平衡位置上方,位移为正,所以加速度为负,有向下的加速度,处于失重状态,故错误;
、时刻,钢球位于平衡位置下方,正在远离平衡位置,速度方向向下,故错误;
、时间内,钢球的速度先增大后减小,动能先增大后减小,故错误;
、时间内,钢球克服弹力做功,根据能量守恒定律可知,钢球的机械能减小,故正确。
故选:。
分析钢球的位移方向,从而找到其加速度方向,再根据超重和失重条件进行分析;
根据图像分析钢球的运动方向;
衡位置钢球的速度增大,远离平衡位置钢球的速度减小;
分析钢球的做功情况,从而分析出钢球的机械能变化情况。
解决该题的关键是知道简谐运动的加速度与位移方向相反,掌握简谐运动的速度变化情况,掌握机械能守恒条件。
2.【答案】
【解析】
【分析】
只有重力和弹力做功,系统机械能守恒,弹簧的弹性势能、物体的动能、重力势能之和不变;在最低点弹性势能最大,根据能量守恒定律,求出最低点的弹性势能.
解决本题的关键抓住简谐运动的对称性以及灵活运用能量守恒定律和机械能守恒定律.
【解答】
A.在运动的过程中,只有重力和弹力做功,系统机械能守恒,弹簧的弹性势能、物体的动能、重力势能之和不变。弹簧的弹性势能是变化的,故物体的重力势能和物体动能总和是变化的,故A错误;
小球在简谐运动的平衡位置处,,所以在最低点时,形变量为,弹力大小为。加速度大小为,故BC错误;
D.从最高点到最低点,动能变化为,重力势能减小,则弹性势能增加而初位置弹性势能为,在最低点弹性势能最大,为故D正确。
故选D。
3.【答案】
【解析】
【分析】
根据简谐运动的特点分析出小球的运动是否属于简谐运动;
分析出小球压缩弹簧过程中的受力特点和速度变化特点,由此完成分析;
分阶段分析出小球在匀速阶段的时间和与弹簧作用阶段的时间与速度的关系,最后完成分析。
本题主要考查了简谐运动的相关应用,理解简谐运动的回复力和位移的关系,同时熟记简谐运动的周期公式即可完成解答。
【解答】
A.物体做简谐运动的条件是在运动过程中所受回复力与位移成正比,且方向始终指向平衡位置,可知小球在杆中点到接触弹簧过程中,所受合力为零,故小球不是做简谐运动,故A错误;
假设杆中点为,小球向右压缩弹簧至最大压缩量时的位置为,小球向左压缩弹簧至最大压缩量时的位置为,可知小球做周期为的往复运动,运动过程为,根据对称性可知小球从与,这两个过程的动能变化完全一致,两根弹簧的总弹性势能的变化完全一致,故小球动能的变化周期为,两根弹簧的总弹性势能的变化周期为,其中一根弹簧的弹性势能变化的周期为,故B错误,C正确;
D.小球的初速度为时,可知小球在匀速阶段的时间变为原来的倍,接触弹簧过程,根据弹簧振子的周期公式可知,接触弹簧过程中所用时间与速度无关,故D错误。
故选C。
4.【答案】
【解析】
【分析】
本题考查弹簧振子,振动系统的机械能守恒,即动能与弹性势能之和守恒,根据最大位移处求,根据平衡位置处求速度。
最大位移处加速度最大,根据牛顿第二定律求解加速度。
【解答】
A、根据题意,系统具有总能量,因为弹簧振子在光滑水平面上做简谐振动,弹簧的最大伸长量等于振幅,有,
解得,故A错误;
B、振子经过平衡位置时,弹簧伸长量为零,弹性势能为零,振子经过平衡位置时的动能,根据,解得,故B错误;
C、弹簧的最大加速度大小为,故C正确;
D、振子在最大位移处时系统只有弹性势能,质量突变为,振动系统的总能量不变,振幅不变,故D错误。
故选C。
5.【答案】
【解析】
【分析】
本题结合弹簧振子的振动图像考查弹簧振子的振动规律。解决问题的关键是能从振动图像读取有关信息,比如周期,振幅,熟悉描述振动的物理量之间的关系。
【解答】
从图中直接可以看出甲的振幅为,乙的振幅,甲的周期,乙的周期。
、甲、乙两弹簧振子的振动周期之比为,根据,两者的频率之比为,故错误;
、甲振动了个周期,路程为,乙振动了个周期,路程为,故路程之比为,故正确;
、根据胡克定律可知,甲、乙的最大回复力之比为,又因为两球质量之比是,根据牛顿第二定律可知,甲、乙两弹簧振子最大加速度之比是,故错误;
、经分析,当到达平衡位置时,速度最大,设此时最大速度为,甲弹簧振子的弹簧伸长量为,在最低点时的弹簧伸长量为,则有: ,从最低点到平衡位置时,根据动能定理得: ,又因为 ,联立解得,所以最大速度之比为,故错误。
6.【答案】
【解析】
【分析】
用简谐运动的条件和机械波的特点分析;
根据单摆运动的特点进行分析;
当孔、缝的宽度与波长差不多或者比波长小时,就能够发生明显的衍射现象,这是发生明显衍射的条件;
频率相同的两列水波的叠加:当波峰与波峰、波谷与波谷相遇时振动是加强的;当波峰与波谷相遇时振动是减弱的。
【解答】
、光滑斜面上的金属球做简谐运动,回复力由弹簧弹力与重力沿斜面方向的分力的合力提供,故正确;
、单摆的摆角较小时,运动为简谐运动,回复力由重力沿切线方向的分力提供,故错误;
、若增大波源点振动的频率,由可知波长变短,衍射现象会更不明显,故错误;
、点和点是波峰与波峰、点是波谷与波谷相遇的点,都是振动加强的点,在它们连线上的点也是振动加强点,它们的振幅最大,但是在振动过程中位移会不断变化,当他们振动到平衡位置时,位移为零,故错误。
7.【答案】
【解析】
【分析】
根据弹簧振子的图象,当振子在平衡位置时速度最大,加速度为零;当偏离平衡位置距离最大时,速度为零,加速度最大;其中加速度方向始终指向平衡位置,速度方向看下一时刻的运动情况即可判断。
本题考查了弹簧振子的简谐振动图象,解题的关键是把握住振动图象中,速度、加速度的大小与方向的判断,有一定规律性,平时注意积累。
【解答】
A.时,物块处于振幅最大处,方向指向平衡位置,因此加速度最大且方向为负方向,水平向左,故A错误;
B.时,物块处于平衡位置,速度最大,下一时刻向下运动,速度方向为负方向,水平向左,故B错误;
C.时,物块处于负向振幅最大处,方向指向平衡位置,因此加速度最大且方向为正方向,水平向右,加速度大小相同,方向相同,故物块加速度最大,所受的摩擦力最大,方向水平向右,故C错误;
D.一起以点为平衡位置,沿光滑水平面在、两点之间做简谐运动,周期为,故物块所受回复力即摩擦力也随时间做周期性的变化,周期为,故D正确。
8.【答案】
【解析】
【分析】
该题考查波的图像相关知识。不考虑能量损耗,各质点振幅相同;根据“带动法”分析速度方向;根据回复力分析加速度方向;根据质点振动情况分析谁先到达平衡位置。
【解答】
A.各质点均做受迫振动,不考虑能量损耗,各质点振幅相同,故A正确;
B.根据“带动法”可知,此时速度方向向上,速度方向向下,故B错误;
C.和两质点均在平衡位置上方,回复力均向下,加速度方向均向下,故C正确;
D.此时和两质点都向上运动,比先到达最大位移处,先回到平衡位置,故D正确。
故选ACD。
9.【答案】
【解析】
【分析】
结合受力分析,确定的平衡位置,然后结合题目的条件即可求出振幅最大值;当运动至最低点时,弹簧的压缩量最大,结合受力情况即可求解对挡板的最大压力。
该题考查简谐振动的受力问题,掌握简谐运动的特点即可解答。
【解答】
若做简谐振动,则位于平衡位置时,沿斜面方向受到的合外力等于,而沿斜面的方向上有重力的分力和弹簧的弹力,可知二者大小相等,方向相反,即,所以,由题意,向上到达的最高点的位置时,弹簧的长度恰好等于原长是仍然能做简谐振动的最高点,所以的最大振幅,,故A正确,B错误;
以增大振幅振动时,由简谐振动的特点可知到达最低点时,弹簧的压缩量;以为研究对象,则受到重力、斜面的支持力、挡板的支持力和弹簧沿斜面向下的压力,沿斜面的方向,联立得,由牛顿第三定律可知以最大振幅振动时,对挡板的最大压力为,故C错误,D正确。
10.【答案】
【解析】
【分析】
结合受力分析,确定的平衡位置,然后结合题目的条件即可求出振幅最大值;当运动至最低点时,弹簧的压缩量最大,结合受力情况即可求解对挡板的最大压力。
该题考查简谐振动的受力问题,掌握简谐运动的特点即可解答。
【解答】
若做简谐振动,则位于平衡位置时,沿斜面方向受到的合外力等于,而沿斜面的方向上有重力的分力和弹簧的弹力,可知二者大小相等,方向相反,即,所以,由题意,向上到达的最高点的位置时,弹簧的长度恰好等于原长是仍然能做简谐振动的最高点,所以的最大振幅,,故A正确,B错误;
以增大振幅振动时,由简谐振动的特点可知到达最低点时,弹簧的压缩量;以为研究对象,则受到重力、斜面的支持力、挡板的支持力和弹簧沿斜面向下的压力,沿斜面的方向,联立得,由牛顿第三定律可知以最大振幅振动时,对挡板的最大压力为,故C错误,D正确。
11.【答案】
【解析】解:时物块刚接触薄板,落至薄板上后和薄板始终粘连,构成竖直方向的弹簧振子,并且从图像看,以后的图像为正弦函数曲线,故A正确;
B.薄板为轻质薄板,质量可忽略不计。由图乙可知,点是图像的最高点,点是图像最低点,根据简谐运动的对称性可知,最高点的加速度和最低点的加速度大小相等,即,由简谐运动的加速度满足
可知,与成正比,设点处的偏离平衡位置位移大小为,点处偏离平衡位置的位移大小为,有,所以,故,到点时,物块只受重力,,所以,故B正确;
C.弹簧振子的周期只与震动系统本身有关,与物块起始下落的高度无关,故物块与薄板粘连后震动周期不变,故C错误;
D.由图乙可知,
振幅为,后物块位置随时间变化关系式为
当时,,代入上式得
所以
故D正确。
故选:。
物块与薄板一起运动时是简谐运动,根据简谐运动的对称性确定物块的加速度;分析运动过程中物块的受力情况,根据牛顿第二定律分析加速度的变化;根据简谐运动的角速度,振幅可解得位置随时间的表达式。
解决本题的关键是要分析清楚物块的运动过程和受力情况,掌握简谐运动的对称性,来分析物块所受合外力的变化情况,掌握简谐运动的特点。
12.【答案】
【解析】
【分析】
摆球在摆动的过程中,在最低点时拉力最大,根据牛顿第二定律分析拉力与速度的关系,从而判断出机械能的变化.摆球在摆动的过程中,一个周期内两次经过最低点。
由图读出两单摆的周期,由单摆的周期公式分析摆长关系;由位移的最大值读出振幅;由于两摆的质量未知,无法比较机械能的大小;根据加速度与位移方向相反,确定加速度的方向。
【解答】
摆球经过最低点时,拉力最大,由图知在时,拉力最大,所以此时摆球经过最低点;在时,摆球的拉力最小,不是经过最低点,故A正确,B错误;
C.在最低点,根据牛顿第二定律得:,则在最低点的拉力减小,可知小球的速度减小,机械能减小,故C正确;
D.在一个周期内摆球两次经过最低点,根据图象知周期故D错误;
故选AC。
由图看出,两单摆的周期相同,同一地点相同,由单摆的周期公式得知,甲、乙两单摆的摆长相等.故A正确;
B.甲摆的振幅为,乙摆的振幅为,则甲摆的振幅比乙摆大.故B正确;
C.尽管甲摆的振幅比乙摆大,两摆的摆长也相等,但由于两摆的质量未知,无法比较机械能的大小.故C错误;
D.在时,甲摆经过平衡位置,振动的加速度为零,而乙摆的位移为负的最大,则乙摆具有正向最大加速度.故D正确;
故选ABD。
13.【答案】
振子的运动
位移 方向 向右 向左 向左 向右
大小 减小 增大 减小 增大
回复力 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
加速度 方向 向左 向右 向右 向左
大小 减小 增大 减小 增大
速度 方向 向左 向左 向右 向右
大小 增大 减小 增大 减小
振子的动能 增大 减小 增大 减小
弹簧的势能 减小 增大 减小 增大
系统总能量 不变 不变 不变 不变
向下向下
【解析】根据简谐振动规律解答即可,点为平衡位置,可判断位移的方向和大小的变化,回复力总是指向平衡位置,衡位置回复力减小,远离平衡位置回复力增大,根据牛顿第二定律,加速度的变化与回复力的变化时一致的,动能与弹性势能相互转化,衡位置弹性势能减小,动能增大,远离则反之。所以答案分别为增大、向右、减小、向左、增大、减小。
根据题意可知时质点开始向上振动,时,质点振动了,则其振动方向向下;振动从质点传播到质点经过,则质点到质点的距离为,所以则点到质点之间的距离为,波从质点传播到质点的时间为,故时,质点振动了,正向下振动。
小球碰前和碰后的速度都用平抛运动来测定,即而由知,每次竖直高度相等,平抛时间相等.即;则可得故只需测量射程,因而选C.
由表达式知:在已知时,需测量、、和,故必要步骤、、.
若为弹性碰撞,同时还满足机械能守恒.
14.【答案】解:物体平衡时,受重力、支持力和弹簧的弹力,根据平衡条件,有:
解得:
故弹簧的长度为;
物体做简谐运动的振幅为:
;
物体到达平衡位置下方位置时,弹力为:;
故合力为:;
故物体做简谐运动;
答:物块处于平衡位置时弹簧的长度为;
物块做简谐运动的振幅是;
证明如上.
【解析】物体平衡时,受重力、支持力和弹簧的弹力,三力平衡,根据平衡条件并结合正交分解法和胡克定律列式求解;
物块做简谐运动的振幅等于物体处于平衡位置时弹簧的伸长量与开始的压缩量的和;
简谐运动中,合力充当回复力,满足条件.
本题关键是对滑块受力分析,利用简谐运动的对称性求解弹簧最大伸长量,明确简谐运动的条件是回复力满足:.
15.【答案】解:小球在一个周期内两次经过最低点,根据该规律,则小球的周期:
由单摆的周期公式为:
解得:
摆球在点和点受力分析如图所示:
在最高点,有:
在最低点设小球的速度为,有:
从到,机械能守恒,由机械能守恒定律得:
联立三式并代入数据得:,
由知,摆球运动过程中的最大速度。
【解析】小球运动到最低点时,绳子的拉力最大,在一个周期内两次经过最低点,根据该规律,求出单摆的周期.再根据单摆的周期公式求出摆长;
小球在最高点时绳子的拉力最小,在最低点时绳子拉力最大,求出最高点和最低点绳子拉力的表达式,再结合动能定理或机械能守恒定律求出摆球的质量;
根据最低点时绳子的拉力最大,结合牛顿第二定律求出摆球的最大速度。
本题考查了单摆周期公式的应用,解决本题的关键掌握单摆的运动规律,知道单摆的周期公式,以及会灵活运用机械能守恒定律、牛顿第二定律解题。
16.【答案】解:弹簧振子以点为平衡位置,在、两点间做简谐运动,所以振幅是之间距离而,所以
由简谐运动的对称性可知到的时间与返回的时间是相等的,所以:;
同时由简谐振动的对称性可知:
又由于:
联立得:
所以:
内路程:
由的分析可知,从时刻,经过时间振子到达点;所以在时刻质点又一次到达点,所以质点的位移是。
答:弹簧振子的振幅是;
弹簧振子振动周期是,频率是;
振子在内通过的路程是;末的位移大小是。
【解析】本题在于关键分析质点的振动情况,确定点的运动方向和周期.写振动方程时要抓住三要素:振幅、角频率和初相位。
由、之间的距离得出振幅;
在时刻,振子从间的点以速度向点运动,经过它的速度大小第一次与相同,方向相反,再经过它的速度大小第二次与相同,方向与原来相反,质点运动到关于平衡位置对称的位置,求出周期。
由、之间的距离得出振幅,结合振子开始计时的位置,求出振子在内通过的路程;结合振子开始计时的位置然后求出末的位移大小。
第2页,共2页
第1页,共1页
