2.4单摆 人教版(2019)高中物理选择性必修一同步练习(含答案解析)
文档属性
| 名称 | 2.4单摆 人教版(2019)高中物理选择性必修一同步练习(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 303.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-07-16 10:38:29 | ||
图片预览




文档简介
2.4单摆人教版( 2019)高中物理选择性必修一同步练习
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共7小题,共28.0分)
有两个同学利用假期分别去参观位于合肥市的“中科大”和北京市的“北京大学”,他们各自在那里的物理实验室利用先进的系统较准确地探究了单摆周期和摆长的关系。然后他们通过互联网交流实验数据,并由计算机绘制了图象,如图甲所示。另外,去“北大”做研究的同学还利用计算机绘制了他实验用的、两个摆球的振动图象,如图乙所示。则下列说法正确的是( )
A. 甲图中“北大”的同学所测得的实验结果对应的图象是
B. 甲图中图线的斜率表示所在位置的重力加速度
C. 由乙图可知,、两摆球振动周期之比为
D. 由乙图可知,、两单摆摆长之比为
有两位同学利用假期分别去参观位于天津市的“南开大学”和上海市的“复旦大学”,他们各自利用那里的实验室中系统探究了单摆周期和摆长的关系。然后通过互联网交流实验数据,并用计算机绘制了如图甲所示的图像。另外,去“复旦大学”做研究的同学还利用计算机绘制了他实验用的、两个摆球的振动图像,如图乙所示。下列说法正确的是
A. 甲图中“南开大学”的同学所测得的实验结果对应的图线是
B. 甲图中图线的斜率表示对应所在位置的重力加速度的倒数
C. 由乙图可知,、两摆球振动周期之比为
D. 由乙图可知,时球振动方向沿轴负方向
将一个摆长为的单摆放在一个光滑的,倾角为的斜面上,其摆角为,如图下列说法正确的是( )
A. 摆球做简谐运动的回复力
B. 摆球做简谐运动的回复力为
C. 摆球做简谐运动的周期为
D. 摆球在运动过程中,经平衡位置时,线的拉力为
一个质量为的小球在半径为的光滑圆弧槽上来回运动,如图,圆弧槽的长度为了使小球振动的频率变为原来的,可以采用的办法是( )
A. 将减小为原来的
B. 将增大为原来的倍
C. 将圆弧长增大为原来的倍
D. 将减小为原来的
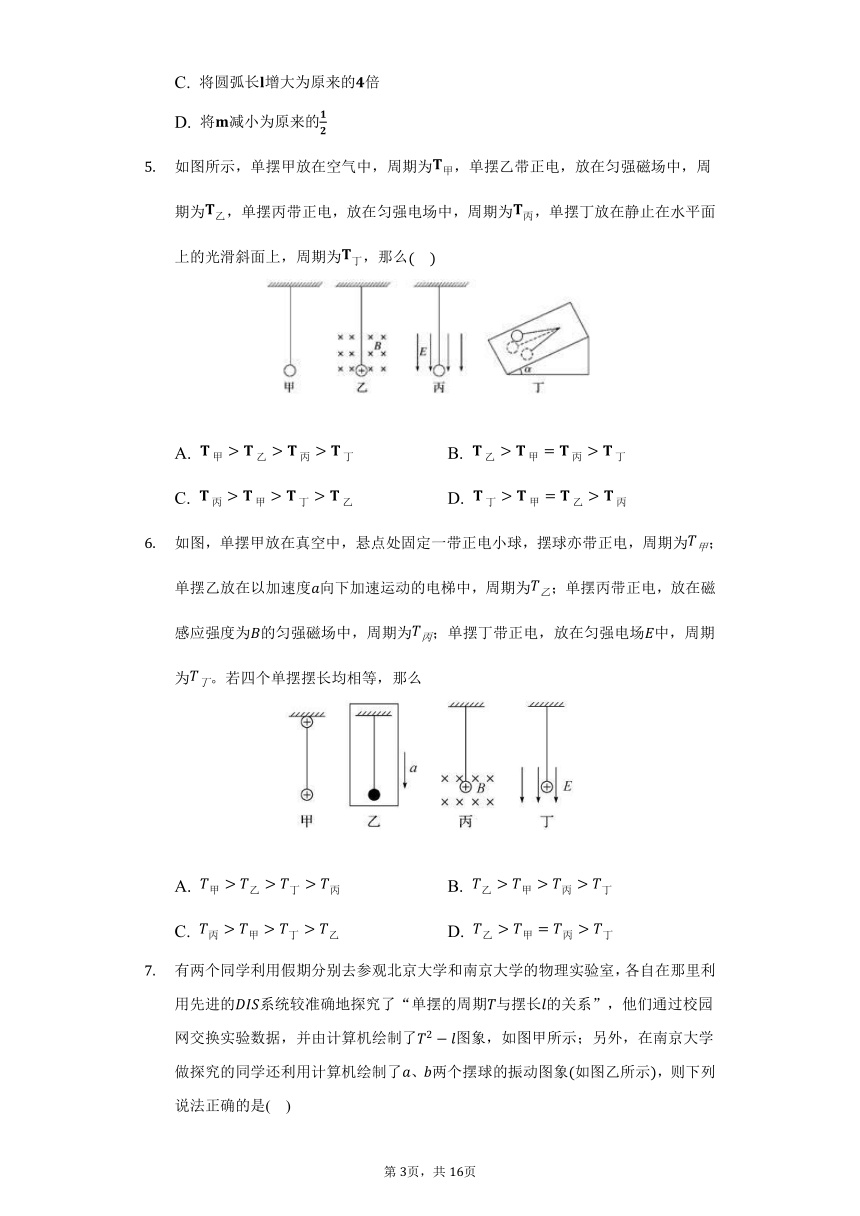
如图所示,单摆甲放在空气中,周期为,单摆乙带正电,放在匀强磁场中,周期为,单摆丙带正电,放在匀强电场中,周期为,单摆丁放在静止在水平面上的光滑斜面上,周期为,那么
A. B.
C. D.
如图,单摆甲放在真空中,悬点处固定一带正电小球,摆球亦带正电,周期为;单摆乙放在以加速度向下加速运动的电梯中,周期为;单摆丙带正电,放在磁感应强度为的匀强磁场中,周期为;单摆丁带正电,放在匀强电场中,周期为。若四个单摆摆长均相等,那么
A. B.
C. D.
有两个同学利用假期分别去参观北京大学和南京大学的物理实验室,各自在那里利用先进的系统较准确地探究了“单摆的周期与摆长的关系”,他们通过校园网交换实验数据,并由计算机绘制了图象,如图甲所示;另外,在南京大学做探究的同学还利用计算机绘制了、两个摆球的振动图象如图乙所示,则下列说法正确的是( )
A. 去北京大学的同学所测实验结果对应图甲中的线
B. 由图乙可知,两单摆摆长之比
C. 在时,球正沿轴负方向运动
D. 在时,球正沿轴正方向运动
二、多选题(本大题共4小题,共16.0分)
如图光滑圆弧槽半径为,为圆弧的最低点,圆弧的最高点到的距离远小于。两个可视为质点的小球和都由静止开始释放。设点到点的距离为,则以下所给的四个值中,可以使、两球在点相遇的是( )
A. B. C. D.
单摆在不同高度处做简谐运动的周期是不同的。摆长为的单摆,在海平面处做简谐运动的周期为;在海拔高度为的高山山顶做简谐运动的周期为;在运行轨道高度为的空间站做简谐运动的周期为。地球可视为半径为、质量为的均匀球体,万有引力常量为。则下列说法正确的是
A. B.
C. D.
如图所示,三根细线于点处打结,、两端固定在同一水平面上相距为的两点上,使成直角三角形,已知线长是,下端点系着一个小球忽略小球半径,下面说法正确的是( )
A. 让小球在纸面内摆动,周期
B. 让小球在垂直纸面方向摆动,周期
C. 让小球在纸面内摆动,周期
D. 让小球在垂直纸面内摆动,周期
多选下列说法正确的是( )
A. 在干涉现象中,振动加强点的位移总比减弱点的位移要大
B. 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关
C. 火车鸣笛向我们驶来时,我们听到的笛声频率将比声源发声的频率高
D. 当水波通过障碍物时,若障碍的尺寸与波长差不多,或比波长大的多时,将发生明显的衍射现象
第II卷(非选择题)
三、实验题(本大题共2小题,共18.0分)
学校物理兴趣小组在游览泰山时,发现一棵三位同学都合抱不过来的千年古树,他们想知道这颗古树的大小。由于他们未带卷尺,只备有救生绳较轻较细,于是他们利用单摆原理对古树的直径进行粗略测量。他们用救生绳绕树一周,截取长度等于树干周长的一段已预留出打结部分的长度,然后在这段救生绳的一端系一个小石块。接下来的操作步骤为:
Ⅰ将截下的救生绳的另一端固定在一根离地足够高的树枝上;
Ⅱ移动小石块,使伸直的救生绳偏离竖直方向一个小的角度小于,然后由静止释放,使小石块在同一竖直面内摆动;
Ⅲ从小石块经过平衡位置已经选定参考位置开始,用手机中的“秒表”软件计时记为第次经过平衡位置,至小石块第次经过平衡位置,测出这一过程所用的总时间为,计算出小石块摆动的周期。
根据步骤Ⅲ,可得小石块摆动的周期__________。
该地区同纬度海平面的重力加速度为,可得该树干的直径__________。
若空气阻力的影响可不计,同时小石块摆动的周期测量结果准确,考虑到泰山的海拔较高,则该树干直径的测量值__________填“”“”或“”真实值。
某同学用图甲所示的装置研究单摆运动的规律,让摆球在竖直平面内做摆动,用力传感器得到细线对摆球拉力的大小随时间变化的图线如图乙所示,且从最低点开始为计时起点由图乙中所给的数据结合力学规律可得
该同学先用游标卡尺测量小球的直径如图丙所示,其读数为___________;
由图像得该单摆的运动周期___________;
摆球的质量___________
四、计算题(本大题共3小题,共30.0分)
正在修建的楼房顶上固定一根不可伸长的细线垂到图示窗沿下,某同学想应用单摆原理测量窗的上沿到房顶的高度,他先将线的下端系上一个小球,当小球静止时,细线恰好与窗子上沿接触且保持竖直,球在最低点时,球心到窗上沿的距离为。他打开窗户,让小球在垂直于墙的竖直平面内作小角度摆动,如图所示,从小球第次通过图中的点开始计时到第次通过点共用时。当地重力加速度值取,根据以上数据,求:
该单摆的周期;
房顶到窗上沿的高度。
如图甲所示是一个单摆振动的情形,是它的平衡位置,、是摆球所能到达的最远位置.设摆球向右方向运动为正方向.图乙所示是这个单摆的振动图象.根据图象回答:
单摆振动的频率是多大?
若当地的重力加速度为,试求这个摆的摆长是多少?
如果摆球在处绳上拉力,在处绳上拉力,则摆球质量是多少?
正在修建的楼房顶上固定一根不可伸长的细线垂到图示窗沿下,某同学想应用单摆原理测量窗的上沿到房顶的高度,他先将线的下端系上一个小球,当小球静止时,细线恰好与窗子上沿接触且保持竖直,球在最低点时,球心到窗上沿的距离为。他打开窗户,让小球在垂直于墙的竖直平面内作小角度摆动,如图所示,从小球第次通过图中的点开始计用入到第次通过点共用时。当地重力加速度值取,根据以上数据,求:
该单摆的周期;
房顶到窗上沿的高度。
答案和解析
1.【答案】
【解析】
【分析】
根据两个摆球的振动图象得出周期的关系,结合单摆的周期公式求出两个单摆的摆长之比;根据单摆的周期公式得出关系式,结合图线的斜率比较重力加速度的大小,确定哪个图线是“北大”的同学测得。
本题考查了单摆的周期公式和图线的综合运用,通过图线得出单摆的周期之比是关键,知道图线斜率的物理意义。
【解答】
根据得,,知图线的斜率,图线的斜率较小,则图线对应的重力加速度较大,可知甲图中“北大”的同学所测得的实验结果对应的图象是,故AB错误;
C.周期等于完成一次全振动的时间,由乙图可知,、两单摆的周期之比为:,故C错误;
D.根据得,,因为、的周期之比为:,则摆长之比为:,故D正确。
故选D。
2.【答案】
【解析】
【分析】
根据两个摆球的振动图象得出周期的关系,结合单摆的周期公式求出两个单摆的摆长之比;根据单摆的周期公式得出关系式,结合图线的斜率比较重力加速度的大小,确定哪个图线是“南开大学”的同学测得。
本题考查了单摆的周期公式和图线的综合运用,通过图线得出单摆的周期之比是关键,知道图线斜率的物理意义。
【解答】
根据得:,知图线的斜率。图线的斜率较小,则图线对应的重力加速度较大。复旦的重力加速度比南开的重力加速度小。可知甲图中“南开大学”的同学所测得的实验结果对应的图象是。故AB错误;
C.周期等于完成一次全振动的时间,由乙图可知,、两单摆的周期之比为:,故C错误;
D.由乙图可知,时,球在平衡位置,经很短时间,其位移为负,故振动方向沿轴负方向。故D正确。
故选D。
3.【答案】
【解析】解:、、本题是类似单摆模型,回复力是重力的下滑分力的切向分量提供,重力的下滑分力为,下滑分力的切线分力为,故A正确,B错误;
C、类似单摆模型,等效重力加速度为,故周期为:,故C错误;
D、摆球在运动过程中,经平衡位置时,线的拉力和重力的下滑分力的合力提供向心力,故,故,故D错误;
故选:。
本题是类似单摆模型,小球做简谐运动,回复力是重力的下滑分力的切向分量提供,等效重力加速度为.
本题关键是建立运动模型,找出回复力来源,确定等效重力加速度,不难.
4.【答案】
【解析】
【分析】
该题考查了单摆的周期公式,会通过该公式分析对单摆周期的影响因素,知道单摆的运动摆角应不大于,对于该题,是把小球的运动看做单摆的条件.
【解答】
在小球来回运动的过程中,因,所以小球的运动是简谐运动,其摆长为,则其运动周期为:.
A、将减小为原来的,周期变为原来的原来的,频率则为原来的倍.选项A错误.
B、将增大为原来的倍,周期变为原来的倍,频率则为原来的,选项B正确.
C、将圆弧长增大为原来的倍,不会改变小球运动的周期和频率,选项C错误.
D、小球的周期和频率与质量没有关系,所以改变小球的质量,不会改变其运动的周期和频率,选项D错误.
故选:
5.【答案】
【解析】
【分析】
图乙中,合力的法向分量不变,故等效重力加速度为;图丙中,电场力向下,等效重力加速度为:;根据单摆周期公式列式求解。
本题关键是明确单摆模型的定义,知道单摆的周期公式,能够求解出等效重力加速度,不难。
【解答】
甲图为单摆,可知:;
对乙有电荷受到的洛伦兹力在法线方向没有分力,不影响单摆的周期,即:;
根据等效重力加速度的求法,在平衡位置处且相对静止时受力情况对丙有:,其等效重力加速度为,则;
对丁有:,其等效重力加速度为,则;
由此可知
故D正确,ABC错误。
6.【答案】
【解析】
【分析】
本题关键是明确单摆模型的定义,知道单摆的周期公式,能够求解出等效重力加速度,不难。
【解答】
根据单摆周期公式,知等效重力加速度越小,周期越大;
甲、丙中合力切线方向的分力为重力沿切线方向的分力,等效加速度,
乙图中的等效重力加速度,
丁图中的等效重力加速度,
,
故
故选:。
7.【答案】
【解析】
【分析】
由得,,知图象的斜率越大,则重力加速度越小;由知,两单摆摆长之比,摆球在最大位移时,速度为零。
解决本题的关键知道单摆的周期公式,以及知道图象的斜率表示什么,学会根据振动图线判断摆球速度和位移。
【解答】
A.由单摆的周期公式得图象的斜率,重力加速度越大,斜率越小,我们知道北京的重力加速度比南京的大,所以去北京大学的同学所测实验结果对应的图线是,故选项A错误;
B.从图乙可以得出,由知,两单摆摆长之比,故选项B正确;
C.从题图乙可以看出,时球正处在负最大位移处,此时的速度为零,故选项C错误;
D.时球正通过平衡位置,向负最大位移处运动,故选项D错误。
故选B。
8.【答案】
【解析】
【分析】
本题考查了关于单摆的周期的计算问题,学习中要注意各种的单摆模型,分析出球做简谐运动以及明确两球相遇时的时间之间的关系是解决该题的关键。
【解答】
解:由题意知球做简谐运动,球做自由落体运动,、两球相遇必在点。
球做简谐运动,周期
球从静止开始释放至到达点经历的时间为:
球落到点的时间:
因为相遇时
所以
当时,
当时,
当时,
故BC错误,AD正确。
故选:。
9.【答案】
【解析】分析:
根据单摆周期公式,结合重力加速度表达式分析即可。
解答:
设海平面处的重力加速度为,根据重力等于万有引力,解得,
在海平面处做简谐运动的周期为,故B正确,A错误
C.设海拔高度为的高山山顶的重力加速度为,根据重力等于万有引力,解得,在海平面处做简谐运动的周期为,故C正确
D.单摆在运行轨道高度为的空间站中处于完全失重状态,单摆能够摆动为空间站旋转产生的等效重力的效果,因此不能用单摆周期公式去计算在运行轨道高度为的空间站做简谐运动的周期,故D错误。
10.【答案】
【解析】
【分析】
单摆周期公式,当小球在纸面内做小角度振动时,圆心是点;当小球在垂直纸面方向做小角度振动时,圆心在墙壁上且在点正上方。
本题关键找出摆长,然后根据单摆的周期公式列式求解,基础题。
【解答】
、当小球在纸面内做小角度振动时,圆心是点,摆长为,故周期为,故A正确,C错误;
、当小球在垂直纸面方向做小角度振动时,圆心在墙壁上且在点正上方,摆长为,
故周期为,故B错误,D正确;
故选:。
11.【答案】
【解析】
【分析】
两列波发生干涉时,振动加强处的质点,振幅增大,但振动加强点仍在振动,位移仍在周期性变化;
受迫振动的周期等于驱动力的周期;
多普勒效应中声波靠近人过程中频率增加;
能够发生明显衍射的条件:只要障碍物或者小孔的几何尺寸小于波长,就能发生衍射现象。
本题考查机械振动等知识点,解决本题的关键是熟练掌握相关知识点。
【解答】
A.两列波发生干涉时,如果两列波的波峰在点相遇,质点的振动加强,振幅增大,但点仍振动,位移仍在周期性变化,故A错误;
B.受迫振动的周期等于驱动力的周期,故与摆长无关,故B正确;
C.火车鸣笛向我们驶来时,声波与人间距减小,间距越小声波频率越高,我们听到的笛声频率将比声源发声的频率高,故C正确;
D.能够发生明显衍射的条件:只要障碍物或者小孔的几何尺寸小于波长,就能发生衍射现象,故D错误。
故选BC。
12.【答案】
【解析】
【分析】
根据每经过两次平衡位置为一个周期即可求出周期的大小;
利用单摆周期公式得出摆长的大小,进而根据摆长与树干直径的关系求出树干直径;
根据单摆的周期公式判断出周期与摆长的关系即可得出结论。
本题是一道考查单摆运动的比较新颖的题目,但是本质上没变,还是要从单摆的本质上进行分析即可。
【解答】
根据根据每经过两次平衡位置为一个周期即可得出周期;
单摆周期公式可得摆长,根据圆周周长与半径的关系可知:,所以直径;
根据单摆周期公式可知,山顶的海拔较高,所以实际重力加速度较小,所以同纬度的重力加速度偏大,则测量值大于真实值。
故答案为:;;。
13.【答案】;;。
【解析】
【分析】
游标卡尺主尺与游标尺示数之和是游标卡尺示数;
当单摆经过最低点是速度最大,绳的拉力最大,一个周期单摆两次经过最低点;
根据圆周运动规律、动能定理求解;
【解答】
由图示游标卡尺可知,其示数为:;
当单摆经过最低点是速度最大,绳的拉力最大,一个周期单摆两次经过最低点;
结合图乙可知,;
设最大摆角为,有
从最高点到最低点由动能定理得
联立解得。
故答案为;;。
14.【答案】解:从小球第次通过图中的点开始计用入到第次通过点共用时,则周期为
球心到窗上沿的距离,由于该单摆在左右两侧摆动的摆长变化,故周期公式为
值取,代入数据解得,房顶到窗上沿的高度为:
答:该单摆的周期为;
房顶到窗上沿的高度为。
【解析】把秒表记录摆球一次全振动的时间作为周期,误差较大,应采用累积法测量周期;
根据单摆的周期公式列式求解房顶到窗上沿的高度.
本题关键建立单摆模型,明确测量原理,然后根据单摆的周期公式列式求解,基础题.
15.【答案】解:由图乙可知:
则
由,得:.
在点,摆球沿绳子方向受力平衡,有:
在点有:
从点到点根据机械能守恒有:
联立可得摆球质量:
答:单摆振动的频率是;
这个摆的摆长是;
摆球质量是.
【解析】单摆做简谐运动,完成一次全振动的时间为一个周期,图上相邻两个最大值之间的时间间隔为一个周期.由图象求出单摆的周期,然后求出频率。
已知单摆周期与当地的重力加速度,由单摆周期公式的变形公式可以求出摆长。
处绳子的拉力等于重力的切向分力,处绳子的张力和重力的合力提供向心力,根据牛顿第二定律和机械能守恒定律列式求解即可。
本题关键是明确摆球的运动学规律和动力学规律,然后结合牛顿第二定律和机械能守恒定律列式分析,不难。
16.【答案】解:从小球第次通过图中的点开始计用入到第次通过点共用时,则周期为
球心到窗上沿的距离,由于该单摆在左右两侧摆动的摆长变化,故周期公式为
值取,代入数据解得,房顶到窗上沿的高度为:
答:该单摆的周期为;
房顶到窗上沿的高度为。
【解析】把秒表记录摆球一次全振动的时间作为周期,误差较大,应采用累积法测量周期;
根据单摆的周期公式列式求解房顶到窗上沿的高度.
本题关键建立单摆模型,明确测量原理,然后根据单摆的周期公式列式求解,基础题.
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、单选题(本大题共7小题,共28.0分)
有两个同学利用假期分别去参观位于合肥市的“中科大”和北京市的“北京大学”,他们各自在那里的物理实验室利用先进的系统较准确地探究了单摆周期和摆长的关系。然后他们通过互联网交流实验数据,并由计算机绘制了图象,如图甲所示。另外,去“北大”做研究的同学还利用计算机绘制了他实验用的、两个摆球的振动图象,如图乙所示。则下列说法正确的是( )
A. 甲图中“北大”的同学所测得的实验结果对应的图象是
B. 甲图中图线的斜率表示所在位置的重力加速度
C. 由乙图可知,、两摆球振动周期之比为
D. 由乙图可知,、两单摆摆长之比为
有两位同学利用假期分别去参观位于天津市的“南开大学”和上海市的“复旦大学”,他们各自利用那里的实验室中系统探究了单摆周期和摆长的关系。然后通过互联网交流实验数据,并用计算机绘制了如图甲所示的图像。另外,去“复旦大学”做研究的同学还利用计算机绘制了他实验用的、两个摆球的振动图像,如图乙所示。下列说法正确的是
A. 甲图中“南开大学”的同学所测得的实验结果对应的图线是
B. 甲图中图线的斜率表示对应所在位置的重力加速度的倒数
C. 由乙图可知,、两摆球振动周期之比为
D. 由乙图可知,时球振动方向沿轴负方向
将一个摆长为的单摆放在一个光滑的,倾角为的斜面上,其摆角为,如图下列说法正确的是( )
A. 摆球做简谐运动的回复力
B. 摆球做简谐运动的回复力为
C. 摆球做简谐运动的周期为
D. 摆球在运动过程中,经平衡位置时,线的拉力为
一个质量为的小球在半径为的光滑圆弧槽上来回运动,如图,圆弧槽的长度为了使小球振动的频率变为原来的,可以采用的办法是( )
A. 将减小为原来的
B. 将增大为原来的倍
C. 将圆弧长增大为原来的倍
D. 将减小为原来的
如图所示,单摆甲放在空气中,周期为,单摆乙带正电,放在匀强磁场中,周期为,单摆丙带正电,放在匀强电场中,周期为,单摆丁放在静止在水平面上的光滑斜面上,周期为,那么
A. B.
C. D.
如图,单摆甲放在真空中,悬点处固定一带正电小球,摆球亦带正电,周期为;单摆乙放在以加速度向下加速运动的电梯中,周期为;单摆丙带正电,放在磁感应强度为的匀强磁场中,周期为;单摆丁带正电,放在匀强电场中,周期为。若四个单摆摆长均相等,那么
A. B.
C. D.
有两个同学利用假期分别去参观北京大学和南京大学的物理实验室,各自在那里利用先进的系统较准确地探究了“单摆的周期与摆长的关系”,他们通过校园网交换实验数据,并由计算机绘制了图象,如图甲所示;另外,在南京大学做探究的同学还利用计算机绘制了、两个摆球的振动图象如图乙所示,则下列说法正确的是( )
A. 去北京大学的同学所测实验结果对应图甲中的线
B. 由图乙可知,两单摆摆长之比
C. 在时,球正沿轴负方向运动
D. 在时,球正沿轴正方向运动
二、多选题(本大题共4小题,共16.0分)
如图光滑圆弧槽半径为,为圆弧的最低点,圆弧的最高点到的距离远小于。两个可视为质点的小球和都由静止开始释放。设点到点的距离为,则以下所给的四个值中,可以使、两球在点相遇的是( )
A. B. C. D.
单摆在不同高度处做简谐运动的周期是不同的。摆长为的单摆,在海平面处做简谐运动的周期为;在海拔高度为的高山山顶做简谐运动的周期为;在运行轨道高度为的空间站做简谐运动的周期为。地球可视为半径为、质量为的均匀球体,万有引力常量为。则下列说法正确的是
A. B.
C. D.
如图所示,三根细线于点处打结,、两端固定在同一水平面上相距为的两点上,使成直角三角形,已知线长是,下端点系着一个小球忽略小球半径,下面说法正确的是( )
A. 让小球在纸面内摆动,周期
B. 让小球在垂直纸面方向摆动,周期
C. 让小球在纸面内摆动,周期
D. 让小球在垂直纸面内摆动,周期
多选下列说法正确的是( )
A. 在干涉现象中,振动加强点的位移总比减弱点的位移要大
B. 单摆在周期性外力作用下做受迫振动,其振动周期与单摆的摆长无关
C. 火车鸣笛向我们驶来时,我们听到的笛声频率将比声源发声的频率高
D. 当水波通过障碍物时,若障碍的尺寸与波长差不多,或比波长大的多时,将发生明显的衍射现象
第II卷(非选择题)
三、实验题(本大题共2小题,共18.0分)
学校物理兴趣小组在游览泰山时,发现一棵三位同学都合抱不过来的千年古树,他们想知道这颗古树的大小。由于他们未带卷尺,只备有救生绳较轻较细,于是他们利用单摆原理对古树的直径进行粗略测量。他们用救生绳绕树一周,截取长度等于树干周长的一段已预留出打结部分的长度,然后在这段救生绳的一端系一个小石块。接下来的操作步骤为:
Ⅰ将截下的救生绳的另一端固定在一根离地足够高的树枝上;
Ⅱ移动小石块,使伸直的救生绳偏离竖直方向一个小的角度小于,然后由静止释放,使小石块在同一竖直面内摆动;
Ⅲ从小石块经过平衡位置已经选定参考位置开始,用手机中的“秒表”软件计时记为第次经过平衡位置,至小石块第次经过平衡位置,测出这一过程所用的总时间为,计算出小石块摆动的周期。
根据步骤Ⅲ,可得小石块摆动的周期__________。
该地区同纬度海平面的重力加速度为,可得该树干的直径__________。
若空气阻力的影响可不计,同时小石块摆动的周期测量结果准确,考虑到泰山的海拔较高,则该树干直径的测量值__________填“”“”或“”真实值。
某同学用图甲所示的装置研究单摆运动的规律,让摆球在竖直平面内做摆动,用力传感器得到细线对摆球拉力的大小随时间变化的图线如图乙所示,且从最低点开始为计时起点由图乙中所给的数据结合力学规律可得
该同学先用游标卡尺测量小球的直径如图丙所示,其读数为___________;
由图像得该单摆的运动周期___________;
摆球的质量___________
四、计算题(本大题共3小题,共30.0分)
正在修建的楼房顶上固定一根不可伸长的细线垂到图示窗沿下,某同学想应用单摆原理测量窗的上沿到房顶的高度,他先将线的下端系上一个小球,当小球静止时,细线恰好与窗子上沿接触且保持竖直,球在最低点时,球心到窗上沿的距离为。他打开窗户,让小球在垂直于墙的竖直平面内作小角度摆动,如图所示,从小球第次通过图中的点开始计时到第次通过点共用时。当地重力加速度值取,根据以上数据,求:
该单摆的周期;
房顶到窗上沿的高度。
如图甲所示是一个单摆振动的情形,是它的平衡位置,、是摆球所能到达的最远位置.设摆球向右方向运动为正方向.图乙所示是这个单摆的振动图象.根据图象回答:
单摆振动的频率是多大?
若当地的重力加速度为,试求这个摆的摆长是多少?
如果摆球在处绳上拉力,在处绳上拉力,则摆球质量是多少?
正在修建的楼房顶上固定一根不可伸长的细线垂到图示窗沿下,某同学想应用单摆原理测量窗的上沿到房顶的高度,他先将线的下端系上一个小球,当小球静止时,细线恰好与窗子上沿接触且保持竖直,球在最低点时,球心到窗上沿的距离为。他打开窗户,让小球在垂直于墙的竖直平面内作小角度摆动,如图所示,从小球第次通过图中的点开始计用入到第次通过点共用时。当地重力加速度值取,根据以上数据,求:
该单摆的周期;
房顶到窗上沿的高度。
答案和解析
1.【答案】
【解析】
【分析】
根据两个摆球的振动图象得出周期的关系,结合单摆的周期公式求出两个单摆的摆长之比;根据单摆的周期公式得出关系式,结合图线的斜率比较重力加速度的大小,确定哪个图线是“北大”的同学测得。
本题考查了单摆的周期公式和图线的综合运用,通过图线得出单摆的周期之比是关键,知道图线斜率的物理意义。
【解答】
根据得,,知图线的斜率,图线的斜率较小,则图线对应的重力加速度较大,可知甲图中“北大”的同学所测得的实验结果对应的图象是,故AB错误;
C.周期等于完成一次全振动的时间,由乙图可知,、两单摆的周期之比为:,故C错误;
D.根据得,,因为、的周期之比为:,则摆长之比为:,故D正确。
故选D。
2.【答案】
【解析】
【分析】
根据两个摆球的振动图象得出周期的关系,结合单摆的周期公式求出两个单摆的摆长之比;根据单摆的周期公式得出关系式,结合图线的斜率比较重力加速度的大小,确定哪个图线是“南开大学”的同学测得。
本题考查了单摆的周期公式和图线的综合运用,通过图线得出单摆的周期之比是关键,知道图线斜率的物理意义。
【解答】
根据得:,知图线的斜率。图线的斜率较小,则图线对应的重力加速度较大。复旦的重力加速度比南开的重力加速度小。可知甲图中“南开大学”的同学所测得的实验结果对应的图象是。故AB错误;
C.周期等于完成一次全振动的时间,由乙图可知,、两单摆的周期之比为:,故C错误;
D.由乙图可知,时,球在平衡位置,经很短时间,其位移为负,故振动方向沿轴负方向。故D正确。
故选D。
3.【答案】
【解析】解:、、本题是类似单摆模型,回复力是重力的下滑分力的切向分量提供,重力的下滑分力为,下滑分力的切线分力为,故A正确,B错误;
C、类似单摆模型,等效重力加速度为,故周期为:,故C错误;
D、摆球在运动过程中,经平衡位置时,线的拉力和重力的下滑分力的合力提供向心力,故,故,故D错误;
故选:。
本题是类似单摆模型,小球做简谐运动,回复力是重力的下滑分力的切向分量提供,等效重力加速度为.
本题关键是建立运动模型,找出回复力来源,确定等效重力加速度,不难.
4.【答案】
【解析】
【分析】
该题考查了单摆的周期公式,会通过该公式分析对单摆周期的影响因素,知道单摆的运动摆角应不大于,对于该题,是把小球的运动看做单摆的条件.
【解答】
在小球来回运动的过程中,因,所以小球的运动是简谐运动,其摆长为,则其运动周期为:.
A、将减小为原来的,周期变为原来的原来的,频率则为原来的倍.选项A错误.
B、将增大为原来的倍,周期变为原来的倍,频率则为原来的,选项B正确.
C、将圆弧长增大为原来的倍,不会改变小球运动的周期和频率,选项C错误.
D、小球的周期和频率与质量没有关系,所以改变小球的质量,不会改变其运动的周期和频率,选项D错误.
故选:
5.【答案】
【解析】
【分析】
图乙中,合力的法向分量不变,故等效重力加速度为;图丙中,电场力向下,等效重力加速度为:;根据单摆周期公式列式求解。
本题关键是明确单摆模型的定义,知道单摆的周期公式,能够求解出等效重力加速度,不难。
【解答】
甲图为单摆,可知:;
对乙有电荷受到的洛伦兹力在法线方向没有分力,不影响单摆的周期,即:;
根据等效重力加速度的求法,在平衡位置处且相对静止时受力情况对丙有:,其等效重力加速度为,则;
对丁有:,其等效重力加速度为,则;
由此可知
故D正确,ABC错误。
6.【答案】
【解析】
【分析】
本题关键是明确单摆模型的定义,知道单摆的周期公式,能够求解出等效重力加速度,不难。
【解答】
根据单摆周期公式,知等效重力加速度越小,周期越大;
甲、丙中合力切线方向的分力为重力沿切线方向的分力,等效加速度,
乙图中的等效重力加速度,
丁图中的等效重力加速度,
,
故
故选:。
7.【答案】
【解析】
【分析】
由得,,知图象的斜率越大,则重力加速度越小;由知,两单摆摆长之比,摆球在最大位移时,速度为零。
解决本题的关键知道单摆的周期公式,以及知道图象的斜率表示什么,学会根据振动图线判断摆球速度和位移。
【解答】
A.由单摆的周期公式得图象的斜率,重力加速度越大,斜率越小,我们知道北京的重力加速度比南京的大,所以去北京大学的同学所测实验结果对应的图线是,故选项A错误;
B.从图乙可以得出,由知,两单摆摆长之比,故选项B正确;
C.从题图乙可以看出,时球正处在负最大位移处,此时的速度为零,故选项C错误;
D.时球正通过平衡位置,向负最大位移处运动,故选项D错误。
故选B。
8.【答案】
【解析】
【分析】
本题考查了关于单摆的周期的计算问题,学习中要注意各种的单摆模型,分析出球做简谐运动以及明确两球相遇时的时间之间的关系是解决该题的关键。
【解答】
解:由题意知球做简谐运动,球做自由落体运动,、两球相遇必在点。
球做简谐运动,周期
球从静止开始释放至到达点经历的时间为:
球落到点的时间:
因为相遇时
所以
当时,
当时,
当时,
故BC错误,AD正确。
故选:。
9.【答案】
【解析】分析:
根据单摆周期公式,结合重力加速度表达式分析即可。
解答:
设海平面处的重力加速度为,根据重力等于万有引力,解得,
在海平面处做简谐运动的周期为,故B正确,A错误
C.设海拔高度为的高山山顶的重力加速度为,根据重力等于万有引力,解得,在海平面处做简谐运动的周期为,故C正确
D.单摆在运行轨道高度为的空间站中处于完全失重状态,单摆能够摆动为空间站旋转产生的等效重力的效果,因此不能用单摆周期公式去计算在运行轨道高度为的空间站做简谐运动的周期,故D错误。
10.【答案】
【解析】
【分析】
单摆周期公式,当小球在纸面内做小角度振动时,圆心是点;当小球在垂直纸面方向做小角度振动时,圆心在墙壁上且在点正上方。
本题关键找出摆长,然后根据单摆的周期公式列式求解,基础题。
【解答】
、当小球在纸面内做小角度振动时,圆心是点,摆长为,故周期为,故A正确,C错误;
、当小球在垂直纸面方向做小角度振动时,圆心在墙壁上且在点正上方,摆长为,
故周期为,故B错误,D正确;
故选:。
11.【答案】
【解析】
【分析】
两列波发生干涉时,振动加强处的质点,振幅增大,但振动加强点仍在振动,位移仍在周期性变化;
受迫振动的周期等于驱动力的周期;
多普勒效应中声波靠近人过程中频率增加;
能够发生明显衍射的条件:只要障碍物或者小孔的几何尺寸小于波长,就能发生衍射现象。
本题考查机械振动等知识点,解决本题的关键是熟练掌握相关知识点。
【解答】
A.两列波发生干涉时,如果两列波的波峰在点相遇,质点的振动加强,振幅增大,但点仍振动,位移仍在周期性变化,故A错误;
B.受迫振动的周期等于驱动力的周期,故与摆长无关,故B正确;
C.火车鸣笛向我们驶来时,声波与人间距减小,间距越小声波频率越高,我们听到的笛声频率将比声源发声的频率高,故C正确;
D.能够发生明显衍射的条件:只要障碍物或者小孔的几何尺寸小于波长,就能发生衍射现象,故D错误。
故选BC。
12.【答案】
【解析】
【分析】
根据每经过两次平衡位置为一个周期即可求出周期的大小;
利用单摆周期公式得出摆长的大小,进而根据摆长与树干直径的关系求出树干直径;
根据单摆的周期公式判断出周期与摆长的关系即可得出结论。
本题是一道考查单摆运动的比较新颖的题目,但是本质上没变,还是要从单摆的本质上进行分析即可。
【解答】
根据根据每经过两次平衡位置为一个周期即可得出周期;
单摆周期公式可得摆长,根据圆周周长与半径的关系可知:,所以直径;
根据单摆周期公式可知,山顶的海拔较高,所以实际重力加速度较小,所以同纬度的重力加速度偏大,则测量值大于真实值。
故答案为:;;。
13.【答案】;;。
【解析】
【分析】
游标卡尺主尺与游标尺示数之和是游标卡尺示数;
当单摆经过最低点是速度最大,绳的拉力最大,一个周期单摆两次经过最低点;
根据圆周运动规律、动能定理求解;
【解答】
由图示游标卡尺可知,其示数为:;
当单摆经过最低点是速度最大,绳的拉力最大,一个周期单摆两次经过最低点;
结合图乙可知,;
设最大摆角为,有
从最高点到最低点由动能定理得
联立解得。
故答案为;;。
14.【答案】解:从小球第次通过图中的点开始计用入到第次通过点共用时,则周期为
球心到窗上沿的距离,由于该单摆在左右两侧摆动的摆长变化,故周期公式为
值取,代入数据解得,房顶到窗上沿的高度为:
答:该单摆的周期为;
房顶到窗上沿的高度为。
【解析】把秒表记录摆球一次全振动的时间作为周期,误差较大,应采用累积法测量周期;
根据单摆的周期公式列式求解房顶到窗上沿的高度.
本题关键建立单摆模型,明确测量原理,然后根据单摆的周期公式列式求解,基础题.
15.【答案】解:由图乙可知:
则
由,得:.
在点,摆球沿绳子方向受力平衡,有:
在点有:
从点到点根据机械能守恒有:
联立可得摆球质量:
答:单摆振动的频率是;
这个摆的摆长是;
摆球质量是.
【解析】单摆做简谐运动,完成一次全振动的时间为一个周期,图上相邻两个最大值之间的时间间隔为一个周期.由图象求出单摆的周期,然后求出频率。
已知单摆周期与当地的重力加速度,由单摆周期公式的变形公式可以求出摆长。
处绳子的拉力等于重力的切向分力,处绳子的张力和重力的合力提供向心力,根据牛顿第二定律和机械能守恒定律列式求解即可。
本题关键是明确摆球的运动学规律和动力学规律,然后结合牛顿第二定律和机械能守恒定律列式分析,不难。
16.【答案】解:从小球第次通过图中的点开始计用入到第次通过点共用时,则周期为
球心到窗上沿的距离,由于该单摆在左右两侧摆动的摆长变化,故周期公式为
值取,代入数据解得,房顶到窗上沿的高度为:
答:该单摆的周期为;
房顶到窗上沿的高度为。
【解析】把秒表记录摆球一次全振动的时间作为周期,误差较大,应采用累积法测量周期;
根据单摆的周期公式列式求解房顶到窗上沿的高度.
本题关键建立单摆模型,明确测量原理,然后根据单摆的周期公式列式求解,基础题.
第2页,共2页
第1页,共1页
