安徽省滁州市定远县吴圩片2021-2022学年七年级下学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县吴圩片2021-2022学年七年级下学期期末考试数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 409.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 09:58:25 | ||
图片预览




文档简介
定远县吴圩片2021-2022学年度七年级教学质量调研试卷
数学试题
注意事项:
1.答题前,请将姓名、考生号、考点、考场号和座位号用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上。
2.全卷共4页。考试时间:120分钟;满分:150分
3.作答单项选择题时,选出每题答案后,用2B铅笔把答题卡上对应题目的信息点框涂黑;如需改动,用橡皮擦干净后,再选涂其它答案。作答非选择题时,用黑色字迹的钢笔或签字笔将答案写在答题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
4.考试结束后,请将答题卡交回。
第I卷(选择题 40分)
一、单项选择题(本大题共10小题,每小题4分,满分40分)
1.计算的平方根结果是( )
A.±2 B.±4 C.2 D.4
2.下列各数中,无理数的个数有( )
-0.3, ,,-π,(相邻两个1之间有1个0),3.1415926,,,(小数部分由连续的非负整数组成).
A.3个 B.4个 C.5个 D.6个
3.已知实数、,若,则下列结论中,不成立的是( )
A. B. C. D.
4.不等式组的解集在数轴上表示为( )
A. B.
C. D.
5.中国抗疫取得了巨大成就,也为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.新型冠状病毒的直径约0.00000009米,用科学记数法表示为( )
A. B. C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
8.若, ,则a,b,c的大小关系是( )
A.a>b=c B.a>c>b C.c>a>b D.b>c>a
9.如图,下列给出的条件中,能判定ACDE的是( )
A.∠A+∠2=180° B.∠1=∠A C.∠1=∠4 D.∠A=∠3
10.如图,已知,平分,平分,则下列结论中:
①;②;③;④,正确的有( )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个正数的两个平方根分别是和,则这个正数是__________.
12.已知不等式组,只有三个整数解,则a的取值范围是_________.
13.因式分解:2a2﹣4ab+2b2=_____.
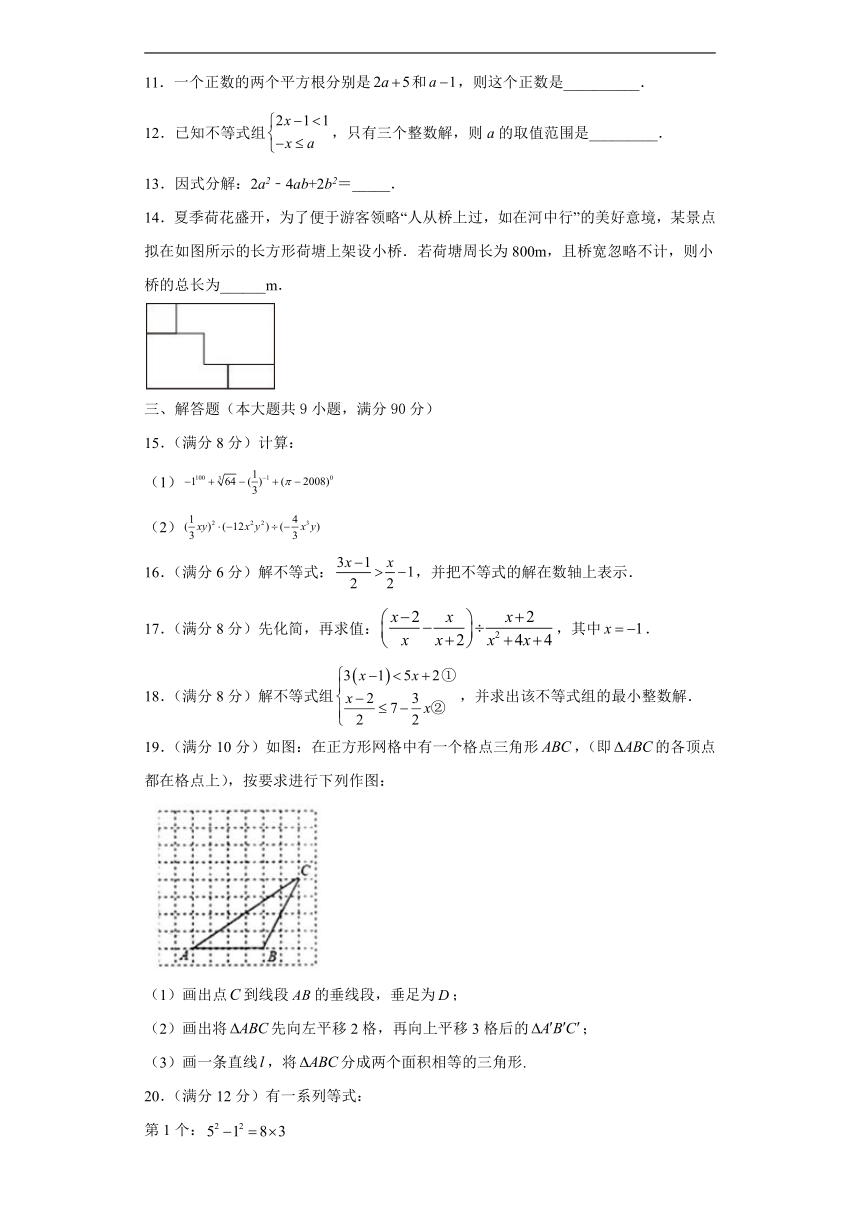
14.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为800m,且桥宽忽略不计,则小桥的总长为______m.
三、解答题(本大题共9小题,满分90分)
15.(满分8分)计算:
(1)
(2)
16.(满分6分)解不等式:,并把不等式的解在数轴上表示.
17.(满分8分)先化简,再求值:,其中.
18.(满分8分)解不等式组,并求出该不等式组的最小整数解.
19.(满分10分)如图:在正方形网格中有一个格点三角形,(即的各顶点都在格点上),按要求进行下列作图:
(1)画出点到线段的垂线段,垂足为;
(2)画出将先向左平移2格,再向上平移3格后的;
(3)画一条直线,将分成两个面积相等的三角形.
20.(满分12分)有一系列等式:
第1个:
第2个:
第3个:
第4个:
……
(1)请写出第5个等式:______.
(2)请写出第n个等式,并加以验证.
(3)依据上述规律,计算:.
21.(满分12分)2020年10月1日,中国﹣安徽滑板公开赛在中国刷业之都、安徽省体育滑板特色小镇——潜山市源潭镇举行,这一运动的兴起也带动了源潭镇的滑板销售.某超市第一次用3000元购进了若干块滑板,很快卖完,由于该滑板畅销,第二次购进时,每块滑板的批发价比第一次提高了20%,所以超市用6000元购进的滑板数量比第一次购进的数量只多了20块,问:
(1)第一次购进的滑板每块批发价是多少元?
(2)如果这两次所购滑板的售价相同,且全部售完后总利润不低于10%,那么每块滑板的售价至少是多少元?
22.(满分12分)阅读:多项式当取某些实数时,是完全平方式.
例如:时,, 发现: ;
时,,发现:;
时,, 发现:;
……
根据阅读解答以下问题:
分解因式:
若多项式是完全平方式,则之间存在某种关系,用等式表示之间的关系:
在实数范围内,若关于的多项式是完全平方式,求值.
求多项式:的最小值.
23.(满分14分)已知,点B为平面内一点,于B.
(1)如图,直接写出和之间的数量关系.
(2)如图,过点B作于点D,求证:.
(3)如图,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF那平分,BE平分,若,,求的度数.
参考答案
1.A 2.B 4.C 5.C 6.D 7.A 8.B 9.B 10.C
11.
12.2≤a<3
13.
14.400
15.(1)1;(2)
解:(1)
(2)解:原式
16.解:
去分母得:,
移项得:,
合并同类项得:,
系数化成1得:,
在数轴上表示为:
.
17.,4
【解析】原式
,
当时,原式.
18.x≤4,-2
解:解不等式①,得: ,
解不等式②,得:,
则不等式组的解集为:,
不等式组的最小整数解为.
19.【详解】
(1)如图所示:即为所求
(2)如图所示:,即为所求;
(3)如图所示:直线EC即为所求.(答案不唯一)
20.解:(1)第1个:,即;
第2个:,即;
第3个:,即;
第4个:,即;
∴第5个等式:,即
故答案为:;
(2)由(1)的规律可得,第n个等式:,验证如下
等式左侧==
等式右侧==
∴
(3)令4n-1=399
解得n=100
∴4n+1=401,4n-3=397
∴=
∴
=
=
=
=
=160800.
21.(1)100元;(2)元
解:(1)设第一次购进的滑板每块批发价是x元,则第二次购进的滑板每块批发价是元,
依题意得:
解得:x=100,
经检验,x=100是原方程的解,且符合题意.
答:第一次购进的滑板每块批发价是100元.
(2)第一次购进滑板的数量为3000÷100=30(块),
第二次购进滑板的数量为(块).
设每块滑板的售价为m元,
依题意得:,
解得:.
答:每块滑板的售价至少是元.
22.(1)(4x-3)2;(2)b2=4ac;(3)m=±20;(4)2.
【解析】(1)16x2-24x+9=(4x-3)2;
(2)b2=4ac;
故答案为(4x-3)2;b2=4ac;
(3)因为m2=4×4×25,
所以m=±20;
(4)x2+y2-4x+6y+15=(x-2)2+(y+3)2+2,
因为(x-2)2≥0,(y+3)2≥0,
所以当x=2,y=-3时,x2+y2-4x+6y+15有最小值2.
23. 【解析】 (1)如图1,
∵,
∴,
∵,
∴,
∴,,
故答案为:;
(2)如图2,过点B作,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,.
(3)如图3,过点B作,
∵BF平分,BE平分,
∴,,
由(2)知,
∴,设,,
则,,,
,
∴
∵,,
∴,
中,由得
,
∵,
∴,
∴,
∴,
∴.
数学试题
注意事项:
1.答题前,请将姓名、考生号、考点、考场号和座位号用黑色字迹的钢笔或签字笔填写在答题卡指定的位置上。
2.全卷共4页。考试时间:120分钟;满分:150分
3.作答单项选择题时,选出每题答案后,用2B铅笔把答题卡上对应题目的信息点框涂黑;如需改动,用橡皮擦干净后,再选涂其它答案。作答非选择题时,用黑色字迹的钢笔或签字笔将答案写在答题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
4.考试结束后,请将答题卡交回。
第I卷(选择题 40分)
一、单项选择题(本大题共10小题,每小题4分,满分40分)
1.计算的平方根结果是( )
A.±2 B.±4 C.2 D.4
2.下列各数中,无理数的个数有( )
-0.3, ,,-π,(相邻两个1之间有1个0),3.1415926,,,(小数部分由连续的非负整数组成).
A.3个 B.4个 C.5个 D.6个
3.已知实数、,若,则下列结论中,不成立的是( )
A. B. C. D.
4.不等式组的解集在数轴上表示为( )
A. B.
C. D.
5.中国抗疫取得了巨大成就,也为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.新型冠状病毒的直径约0.00000009米,用科学记数法表示为( )
A. B. C. D.
6.下列运算正确的是( )
A. B.
C. D.
7.如图,在边长为的正方形中挖掉一个边长为的小正方形,把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
A. B.
C. D.
8.若, ,则a,b,c的大小关系是( )
A.a>b=c B.a>c>b C.c>a>b D.b>c>a
9.如图,下列给出的条件中,能判定ACDE的是( )
A.∠A+∠2=180° B.∠1=∠A C.∠1=∠4 D.∠A=∠3
10.如图,已知,平分,平分,则下列结论中:
①;②;③;④,正确的有( )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.一个正数的两个平方根分别是和,则这个正数是__________.
12.已知不等式组,只有三个整数解,则a的取值范围是_________.
13.因式分解:2a2﹣4ab+2b2=_____.
14.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为800m,且桥宽忽略不计,则小桥的总长为______m.
三、解答题(本大题共9小题,满分90分)
15.(满分8分)计算:
(1)
(2)
16.(满分6分)解不等式:,并把不等式的解在数轴上表示.
17.(满分8分)先化简,再求值:,其中.
18.(满分8分)解不等式组,并求出该不等式组的最小整数解.
19.(满分10分)如图:在正方形网格中有一个格点三角形,(即的各顶点都在格点上),按要求进行下列作图:
(1)画出点到线段的垂线段,垂足为;
(2)画出将先向左平移2格,再向上平移3格后的;
(3)画一条直线,将分成两个面积相等的三角形.
20.(满分12分)有一系列等式:
第1个:
第2个:
第3个:
第4个:
……
(1)请写出第5个等式:______.
(2)请写出第n个等式,并加以验证.
(3)依据上述规律,计算:.
21.(满分12分)2020年10月1日,中国﹣安徽滑板公开赛在中国刷业之都、安徽省体育滑板特色小镇——潜山市源潭镇举行,这一运动的兴起也带动了源潭镇的滑板销售.某超市第一次用3000元购进了若干块滑板,很快卖完,由于该滑板畅销,第二次购进时,每块滑板的批发价比第一次提高了20%,所以超市用6000元购进的滑板数量比第一次购进的数量只多了20块,问:
(1)第一次购进的滑板每块批发价是多少元?
(2)如果这两次所购滑板的售价相同,且全部售完后总利润不低于10%,那么每块滑板的售价至少是多少元?
22.(满分12分)阅读:多项式当取某些实数时,是完全平方式.
例如:时,, 发现: ;
时,,发现:;
时,, 发现:;
……
根据阅读解答以下问题:
分解因式:
若多项式是完全平方式,则之间存在某种关系,用等式表示之间的关系:
在实数范围内,若关于的多项式是完全平方式,求值.
求多项式:的最小值.
23.(满分14分)已知,点B为平面内一点,于B.
(1)如图,直接写出和之间的数量关系.
(2)如图,过点B作于点D,求证:.
(3)如图,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF那平分,BE平分,若,,求的度数.
参考答案
1.A 2.B 4.C 5.C 6.D 7.A 8.B 9.B 10.C
11.
12.2≤a<3
13.
14.400
15.(1)1;(2)
解:(1)
(2)解:原式
16.解:
去分母得:,
移项得:,
合并同类项得:,
系数化成1得:,
在数轴上表示为:
.
17.,4
【解析】原式
,
当时,原式.
18.x≤4,-2
解:解不等式①,得: ,
解不等式②,得:,
则不等式组的解集为:,
不等式组的最小整数解为.
19.【详解】
(1)如图所示:即为所求
(2)如图所示:,即为所求;
(3)如图所示:直线EC即为所求.(答案不唯一)
20.解:(1)第1个:,即;
第2个:,即;
第3个:,即;
第4个:,即;
∴第5个等式:,即
故答案为:;
(2)由(1)的规律可得,第n个等式:,验证如下
等式左侧==
等式右侧==
∴
(3)令4n-1=399
解得n=100
∴4n+1=401,4n-3=397
∴=
∴
=
=
=
=
=160800.
21.(1)100元;(2)元
解:(1)设第一次购进的滑板每块批发价是x元,则第二次购进的滑板每块批发价是元,
依题意得:
解得:x=100,
经检验,x=100是原方程的解,且符合题意.
答:第一次购进的滑板每块批发价是100元.
(2)第一次购进滑板的数量为3000÷100=30(块),
第二次购进滑板的数量为(块).
设每块滑板的售价为m元,
依题意得:,
解得:.
答:每块滑板的售价至少是元.
22.(1)(4x-3)2;(2)b2=4ac;(3)m=±20;(4)2.
【解析】(1)16x2-24x+9=(4x-3)2;
(2)b2=4ac;
故答案为(4x-3)2;b2=4ac;
(3)因为m2=4×4×25,
所以m=±20;
(4)x2+y2-4x+6y+15=(x-2)2+(y+3)2+2,
因为(x-2)2≥0,(y+3)2≥0,
所以当x=2,y=-3时,x2+y2-4x+6y+15有最小值2.
23. 【解析】 (1)如图1,
∵,
∴,
∵,
∴,
∴,,
故答案为:;
(2)如图2,过点B作,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,.
(3)如图3,过点B作,
∵BF平分,BE平分,
∴,,
由(2)知,
∴,设,,
则,,,
,
∴
∵,,
∴,
中,由得
,
∵,
∴,
∴,
∴,
∴.
同课章节目录
