安徽省滁州市定远县育才学校2021-2022学年七年级下学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2021-2022学年七年级下学期期末考试数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-15 10:45:55 | ||
图片预览




文档简介
育才学校2021-2022学年下学期七年级期末考试
数学试题
时间:120分钟;满分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数,-,,,-,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.2020年春季,一种新型冠状病毒嗜虐着人们的健康,据了解,这种新型冠状病毒的直径约为125纳米,若1米纳米,则这种冠病毒的直径用科学记数法可表示为( )
A.米 B.米 C.米 D.米
3.实数a,b在数轴上对应的点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
4.下面计算错误的是( )
A. B.
C. D.
5.若(x+2)(2x-n)=2x2+mx-2,则( )
A.m=3,n=1; B.m=5,n=1; C.m=3,n=-1; D.m=5,n=-1;
6.一元一次不等式组的解集在数轴上表示正确的是( )
A. B.C. D.
7.如图 ,已知1 2 ,3 65 ,那么4 的度数是( )
A.65 B.95 C.105 D.115
8.若,,则的值为( ).
A.4 B.3 C.2 D.0
9.某人将2008看成了一个填数游戏式:2□□8.于是,他在每个框中各填写了一个两位数与,结果发现,所得到的六位数恰是一个完全立方数.则+=( )
A.40 B.50 C.60 D.70
10.若,则的值为( ).
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若,且,则=_________;
12.若与的和仍为单项式,则______.
13.若分式的值为0,则x的值为_____________.
14.RSA129是一个129位利用代数知识产生的数字密码.曾有人认为,RSA129是有史以来最难的密码系统,涉及数论里因数分解的知识,在我们的日常生活中,取款、上网等都需要密码,有一种用“因式分解”法产生的密码方便记忆.如,多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2).若取x=9,y=9时,则各因式的值分别是:x﹣y=0,x+y=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3﹣xy2,若取x=10,y=10,请按上述方法设计一个密码是 __________________.(设计一种即可)
三、解答题(本大题共9题,满分90分)
15.(5分)计算:
16.(6分)解不等式,并将它的解集在数轴上表示出来.
17.(7分)先化简,再求值:,其中x=3.
18.(10分)阅读材料:数形结合是把对形的研究和数的研究统一起来,著名数学家华罗庚先生专门对此赋词一首﹣﹣“数与形,本是相倚依,焉能分作两边飞.数无形时少直觉,形少数时难入微.数形结合百般好,隔离分家万事非:切莫忘,几何代数统一体,永远联系,切莫分离.”这首词形象、生动地强调数形结合的价值,也揭示了数形结合的本质.如图1,A、B、C是三种规格的纸片,用1张A型纸片,1张B型纸片,2张C型纸片,拼成如图2的正方形,用不同方法表示该正方形的面积,可以得到一个公式: (用a、b表示).
观察思考:如果用若干张A、B、C三种规格纸片进行拼图游戏,拼成一个长为(a+2b),宽为(a+b)的长方形,需要A型纸片 张,B型纸片 张,C型纸片 张.
19.(10分)已知:如图,∠1=∠2,∠C=∠D,点B、E分别在线段AC、DF上试说明∠A=∠F.
解:∵∠1=∠2(已知),
∠2=∠3( ),
∴∠1=∠3( ),
∴ ( ),
∴∠C= (两直线平行,同位角相等).
又∵∠C=∠D(已知),
∴ =∠D(等价代换),
∴AC ( ),
∴∠A=∠F ( ).
20.(12分)1261年,我国宋代数学家杨辉写了一本书﹣﹣《详解九章算法》,书中记载了一个用数字排成的三角形,如图1,这个数字三角形原名“开方作法本源图”,是1050~100年间北宋人贾宪做的.后来,我们就把这种数字三角形叫做贾宪三角或杨辉三角,杨辉三角实际是二项式乘方展开式的系数表,如图2所示.
(1)写出杨辉三角中的你所发现的规律(1条即可);
(2)写出(a+b)7展开式中的各项系数;
(3)已知(x﹣1)6=ax6+bx5+cx4+dx3+ex2+fx+1,求a+b+c+d+e+f的值.
21.(12分)我校组织七年级同学上午8:00乘车前往离学校120千米的开化“根博园”开展研学活动,共租了若干辆大巴车,若每辆车坐45人,则余下30人没有车坐;若每辆车坐50人,则最后一辆车还剩10个座位.
(1)七年级共有多少学生?共租了几辆大巴车?
(2)张老师因有事情,8:30从学校自驾汽车以大巴车1.6倍的速度追赶,追上大巴车后继续前行,结果比车队提前15分钟到达“根博园”,求张老师追上大巴车的地点到“根博园”的路程.
22.(14分)如图,已知AD∥BC,CE平分∠BCD,.
(1)CD与EF平行吗?写出证明过程;
(2)若DF平分∠ADC,求证:.
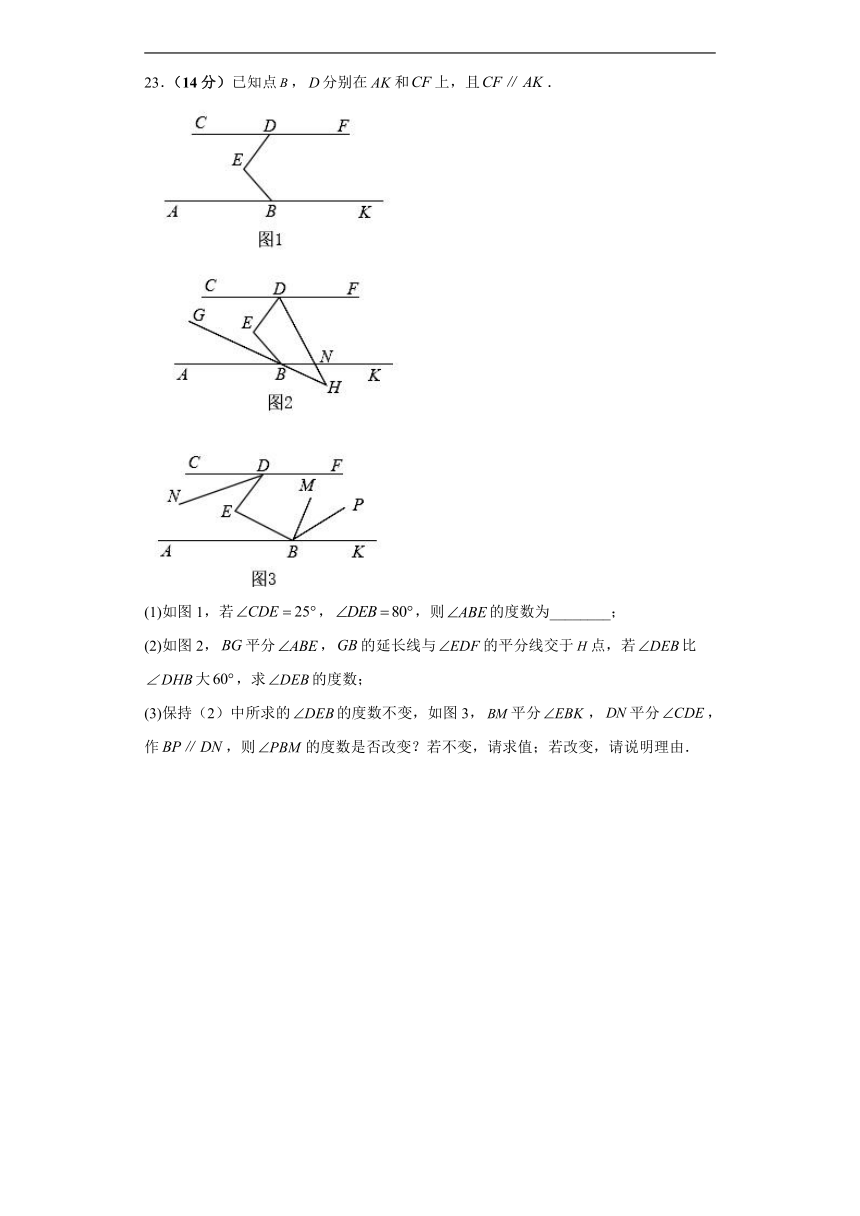
23.(14分)已知点,分别在和上,且.
(1)如图1,若,,则的度数为________;
(2)如图2,平分,的延长线与的平分线交于点,若比大,求的度数;
(3)保持(2)中所求的的度数不变,如图3,平分,平分,作,则的度数是否改变?若不变,请求值;若改变,请说明理由.
参考答案
1.C 2.C 3.D 4.B 5.A 6.A 7.D 8.C 9.D 10.B
11.5或者-5
12.
13.
14.101030(或103010或301010)
15.
解:原式
.
16. 解:
去括号得,x 2x+2≤0,
移项得,x 2x≤ 2,
合并得, x≤ 2,
系数化为1,得x≥2.
解集在数轴上表示为:
17.,
【解析】原式=
=
=.
当x=3时,原式=.
18.阅读材料:(a+b)2=a2+2ab+b2;观察思考:1,2,3.
【解析】阅读材料:大正方形的面积可表示为:(a+b)2或a2+2ab+b2,
则有(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
观察思考:由题意得,长方形的面积为:
(a+2b)(a+b)
=a2+ab+2ab+2b2
=a2+3ab+2b2,
故需要A型纸片1张,B型纸片2张,C型纸片3张.
故答案为:1,2,3.
19.对顶角相等;等量代换;BD;CE;同位角相等,两直线平行;∠ABD;∠ABD;DF;内错角相等,两直线平行;两直线平行,内错角相等.
【解析】∵∠1=∠2(已知),
∠3=∠2 (对顶角相等 ),
∴∠1=∠3 (等量代换 ),
∴BDCE(同位角相等,两直线平行 ),
∴∠C=∠ABD(两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠ABD=∠D(等量代换),
∴ACDF(内错角相等,两直线平行),
∴∠A=∠F (两直线平行,内错角相等).
故答案为:对顶角相等;等量代换;BD;CE;同位角相等,两直线平行;∠ABD;∠ABD;DF;内错角相等,两直线平行;两直线平行,内错角相等.
20.(1)第m行有m个数字(答案不唯一);(2)1,7,21,35,35,21,7,1;(3)﹣1.
【解析】(1)由图表可得:第m行有m个数字(答案不唯一);
(2)(a+b)7展开式中的各项系数为:1,7,21,35,35,21,7,1;
(3)当x=1时,(1﹣1)6=a+b+c+d+e+f+1=0,
∴a+b+c+d+e+f=﹣1;
21.(1)七年级共有390学生,共租了8辆大巴车.
(2)张老师追上大巴车的地点到“根博园”的路程为40千米.
【解析】 (1)设有x辆大巴车,根据题意得:
45x+30=50x-10.
解得:x=8,
∴共有学生45x+30=45×8+30=390(人),
答:七年级共有390学生,共租了8辆大巴车.
(2)设大巴车的的速度为y千米/小时,则张老师驾车的速度为1.6y千米/小时,根据题意得:
解得:y=60
经检验y=60是原方程的解,
1.6x=1.6×60=96,
∴大巴车的的速度为60千米/小时,则张老师驾车的速度为96千米/小时,
∴张老师追上大巴车的时间为:(小时),
∴张老师追上大巴车的地点到“根博园”的路程为:(千米).
22. (1)解:与平行.
平分,
,
又,
,
.
(2)平分,
,
,
,
,
,
,
,
.
23.(1)55° (2)100° (3)不变,40°
(1)解:如图1,过点E作,
∵,
∴,
∴∠CDE=∠DES,∠SEB=∠ABE,
∴∠CDE+∠ABE =∠DES+∠SEB=∠DEB,
∵∠CDE=25°,∠DEB=80°,
∴∠ABE =∠DEB-∠CDE=80°-25°=55°.
故答案为:55°.
(2)解:如图2,延长DE,交AB于点M,
则∠DEB=∠EMB+∠EBM,
∵,平分,
∴∠EMB=180°-∠MDF,∠EBM=2∠ABG=2∠HBN,∠MDH=∠HDF=∠HNK=∠MDF,
∵∠HBN+∠DHB=∠HNK,
∴∠DEB=(180°-∠MDF) +2∠HBN=180°-∠MDF+,
∴∠DEB=180°-∠MDF+∠MDF-2∠DHB=180°-2∠DHB,
∵,
∴∠DEB=180°-2(∠DEB-60°),
∴3∠DEB=300°,
解得∠DEB=100°.
(3)解:过点E作,则,
根据(1)得,∠DEB=∠CDE+∠ABE,
∵平分,平分,
∴∠DEB=2∠NDE+180°-2∠EBM,
∵∠DEB=100°,
∴∠EBM-∠NDE=40°,
∵,
∴∠DEQ=∠NDE,
∴∠EBM =40°+∠DEQ,
∵,
∴,
∴∠EBM+∠PBM +∠BEQ =180°,
∴40°+∠DEQ+∠PBM +∠BEQ =180°,
∴40°+∠DEB+∠PBM =180°,
∴∠PBM =180°-100°-40°=40°,
∴∠PBM 的度数不变,值为40°.
数学试题
时间:120分钟;满分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在实数,-,,,-,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.2020年春季,一种新型冠状病毒嗜虐着人们的健康,据了解,这种新型冠状病毒的直径约为125纳米,若1米纳米,则这种冠病毒的直径用科学记数法可表示为( )
A.米 B.米 C.米 D.米
3.实数a,b在数轴上对应的点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
4.下面计算错误的是( )
A. B.
C. D.
5.若(x+2)(2x-n)=2x2+mx-2,则( )
A.m=3,n=1; B.m=5,n=1; C.m=3,n=-1; D.m=5,n=-1;
6.一元一次不等式组的解集在数轴上表示正确的是( )
A. B.C. D.
7.如图 ,已知1 2 ,3 65 ,那么4 的度数是( )
A.65 B.95 C.105 D.115
8.若,,则的值为( ).
A.4 B.3 C.2 D.0
9.某人将2008看成了一个填数游戏式:2□□8.于是,他在每个框中各填写了一个两位数与,结果发现,所得到的六位数恰是一个完全立方数.则+=( )
A.40 B.50 C.60 D.70
10.若,则的值为( ).
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若,且,则=_________;
12.若与的和仍为单项式,则______.
13.若分式的值为0,则x的值为_____________.
14.RSA129是一个129位利用代数知识产生的数字密码.曾有人认为,RSA129是有史以来最难的密码系统,涉及数论里因数分解的知识,在我们的日常生活中,取款、上网等都需要密码,有一种用“因式分解”法产生的密码方便记忆.如,多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2).若取x=9,y=9时,则各因式的值分别是:x﹣y=0,x+y=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3﹣xy2,若取x=10,y=10,请按上述方法设计一个密码是 __________________.(设计一种即可)
三、解答题(本大题共9题,满分90分)
15.(5分)计算:
16.(6分)解不等式,并将它的解集在数轴上表示出来.
17.(7分)先化简,再求值:,其中x=3.
18.(10分)阅读材料:数形结合是把对形的研究和数的研究统一起来,著名数学家华罗庚先生专门对此赋词一首﹣﹣“数与形,本是相倚依,焉能分作两边飞.数无形时少直觉,形少数时难入微.数形结合百般好,隔离分家万事非:切莫忘,几何代数统一体,永远联系,切莫分离.”这首词形象、生动地强调数形结合的价值,也揭示了数形结合的本质.如图1,A、B、C是三种规格的纸片,用1张A型纸片,1张B型纸片,2张C型纸片,拼成如图2的正方形,用不同方法表示该正方形的面积,可以得到一个公式: (用a、b表示).
观察思考:如果用若干张A、B、C三种规格纸片进行拼图游戏,拼成一个长为(a+2b),宽为(a+b)的长方形,需要A型纸片 张,B型纸片 张,C型纸片 张.
19.(10分)已知:如图,∠1=∠2,∠C=∠D,点B、E分别在线段AC、DF上试说明∠A=∠F.
解:∵∠1=∠2(已知),
∠2=∠3( ),
∴∠1=∠3( ),
∴ ( ),
∴∠C= (两直线平行,同位角相等).
又∵∠C=∠D(已知),
∴ =∠D(等价代换),
∴AC ( ),
∴∠A=∠F ( ).
20.(12分)1261年,我国宋代数学家杨辉写了一本书﹣﹣《详解九章算法》,书中记载了一个用数字排成的三角形,如图1,这个数字三角形原名“开方作法本源图”,是1050~100年间北宋人贾宪做的.后来,我们就把这种数字三角形叫做贾宪三角或杨辉三角,杨辉三角实际是二项式乘方展开式的系数表,如图2所示.
(1)写出杨辉三角中的你所发现的规律(1条即可);
(2)写出(a+b)7展开式中的各项系数;
(3)已知(x﹣1)6=ax6+bx5+cx4+dx3+ex2+fx+1,求a+b+c+d+e+f的值.
21.(12分)我校组织七年级同学上午8:00乘车前往离学校120千米的开化“根博园”开展研学活动,共租了若干辆大巴车,若每辆车坐45人,则余下30人没有车坐;若每辆车坐50人,则最后一辆车还剩10个座位.
(1)七年级共有多少学生?共租了几辆大巴车?
(2)张老师因有事情,8:30从学校自驾汽车以大巴车1.6倍的速度追赶,追上大巴车后继续前行,结果比车队提前15分钟到达“根博园”,求张老师追上大巴车的地点到“根博园”的路程.
22.(14分)如图,已知AD∥BC,CE平分∠BCD,.
(1)CD与EF平行吗?写出证明过程;
(2)若DF平分∠ADC,求证:.
23.(14分)已知点,分别在和上,且.
(1)如图1,若,,则的度数为________;
(2)如图2,平分,的延长线与的平分线交于点,若比大,求的度数;
(3)保持(2)中所求的的度数不变,如图3,平分,平分,作,则的度数是否改变?若不变,请求值;若改变,请说明理由.
参考答案
1.C 2.C 3.D 4.B 5.A 6.A 7.D 8.C 9.D 10.B
11.5或者-5
12.
13.
14.101030(或103010或301010)
15.
解:原式
.
16. 解:
去括号得,x 2x+2≤0,
移项得,x 2x≤ 2,
合并得, x≤ 2,
系数化为1,得x≥2.
解集在数轴上表示为:
17.,
【解析】原式=
=
=.
当x=3时,原式=.
18.阅读材料:(a+b)2=a2+2ab+b2;观察思考:1,2,3.
【解析】阅读材料:大正方形的面积可表示为:(a+b)2或a2+2ab+b2,
则有(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
观察思考:由题意得,长方形的面积为:
(a+2b)(a+b)
=a2+ab+2ab+2b2
=a2+3ab+2b2,
故需要A型纸片1张,B型纸片2张,C型纸片3张.
故答案为:1,2,3.
19.对顶角相等;等量代换;BD;CE;同位角相等,两直线平行;∠ABD;∠ABD;DF;内错角相等,两直线平行;两直线平行,内错角相等.
【解析】∵∠1=∠2(已知),
∠3=∠2 (对顶角相等 ),
∴∠1=∠3 (等量代换 ),
∴BDCE(同位角相等,两直线平行 ),
∴∠C=∠ABD(两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠ABD=∠D(等量代换),
∴ACDF(内错角相等,两直线平行),
∴∠A=∠F (两直线平行,内错角相等).
故答案为:对顶角相等;等量代换;BD;CE;同位角相等,两直线平行;∠ABD;∠ABD;DF;内错角相等,两直线平行;两直线平行,内错角相等.
20.(1)第m行有m个数字(答案不唯一);(2)1,7,21,35,35,21,7,1;(3)﹣1.
【解析】(1)由图表可得:第m行有m个数字(答案不唯一);
(2)(a+b)7展开式中的各项系数为:1,7,21,35,35,21,7,1;
(3)当x=1时,(1﹣1)6=a+b+c+d+e+f+1=0,
∴a+b+c+d+e+f=﹣1;
21.(1)七年级共有390学生,共租了8辆大巴车.
(2)张老师追上大巴车的地点到“根博园”的路程为40千米.
【解析】 (1)设有x辆大巴车,根据题意得:
45x+30=50x-10.
解得:x=8,
∴共有学生45x+30=45×8+30=390(人),
答:七年级共有390学生,共租了8辆大巴车.
(2)设大巴车的的速度为y千米/小时,则张老师驾车的速度为1.6y千米/小时,根据题意得:
解得:y=60
经检验y=60是原方程的解,
1.6x=1.6×60=96,
∴大巴车的的速度为60千米/小时,则张老师驾车的速度为96千米/小时,
∴张老师追上大巴车的时间为:(小时),
∴张老师追上大巴车的地点到“根博园”的路程为:(千米).
22. (1)解:与平行.
平分,
,
又,
,
.
(2)平分,
,
,
,
,
,
,
,
.
23.(1)55° (2)100° (3)不变,40°
(1)解:如图1,过点E作,
∵,
∴,
∴∠CDE=∠DES,∠SEB=∠ABE,
∴∠CDE+∠ABE =∠DES+∠SEB=∠DEB,
∵∠CDE=25°,∠DEB=80°,
∴∠ABE =∠DEB-∠CDE=80°-25°=55°.
故答案为:55°.
(2)解:如图2,延长DE,交AB于点M,
则∠DEB=∠EMB+∠EBM,
∵,平分,
∴∠EMB=180°-∠MDF,∠EBM=2∠ABG=2∠HBN,∠MDH=∠HDF=∠HNK=∠MDF,
∵∠HBN+∠DHB=∠HNK,
∴∠DEB=(180°-∠MDF) +2∠HBN=180°-∠MDF+,
∴∠DEB=180°-∠MDF+∠MDF-2∠DHB=180°-2∠DHB,
∵,
∴∠DEB=180°-2(∠DEB-60°),
∴3∠DEB=300°,
解得∠DEB=100°.
(3)解:过点E作,则,
根据(1)得,∠DEB=∠CDE+∠ABE,
∵平分,平分,
∴∠DEB=2∠NDE+180°-2∠EBM,
∵∠DEB=100°,
∴∠EBM-∠NDE=40°,
∵,
∴∠DEQ=∠NDE,
∴∠EBM =40°+∠DEQ,
∵,
∴,
∴∠EBM+∠PBM +∠BEQ =180°,
∴40°+∠DEQ+∠PBM +∠BEQ =180°,
∴40°+∠DEB+∠PBM =180°,
∴∠PBM =180°-100°-40°=40°,
∴∠PBM 的度数不变,值为40°.
同课章节目录
