黑龙江省哈尔滨市香坊区2012-2013学年度八年级下学期期末调研测试数学试卷(word版)
文档属性
| 名称 | 黑龙江省哈尔滨市香坊区2012-2013学年度八年级下学期期末调研测试数学试卷(word版) |  | |
| 格式 | zip | ||
| 文件大小 | 265.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-07-17 21:34:52 | ||
图片预览




文档简介
香坊区2012—2013学年度下学期期末调研测试
八年级数学试卷
考生须知:本试卷分为第Ⅰ卷和第Ⅱ卷两部分. 第Ⅰ卷为选择题,满分为30分;第Ⅱ卷为填空题和选择题,满分为90分.本试卷共28道题,满分120分,考试时间为120分钟.
题号 一 二 三 总分
得分 21 22 23 24 25 26 27 28
得分
第Ⅰ卷 选择题(共30分)
一、单项选择题(每小题3分,共30分)
1.下列各式中最简二次根式为( )
(A) (B) (C) (D)
2.如果x=-3是方程的一个根,那么m的值是( )
(A)一4 (B)4 (C)3 (D)-3
3.下列计算正确的是( )
(A) (B) (C) (D)
4.关于x的一元二次方程的根的情况是( )
(A)方程没有实数根 (B)方程有两个相等的实数根
(C)方程有两个不相等的实数根 (D)以上答案都不对
5.将方程化成的形式是( )
(A) (B)
(C) (D)
6.如图所示,□ABCD的周长为l6cm,对角线AC与BD相
交于点O,交AD于E,连接CE,则ADCE的
周长为( )
(A)4cm (B)6cm (C)8cm (D)10cm
7.在一幅长90cm,宽40cm的风景画的四周的外边镶宽度相同的金色纸边,制成一幅挂图,
使风景画的面积是整个挂图面积的58%,设金色纸边的宽度为xcm,则可列方程为( )
(A)(90+x)(40+x)×58%=90x40 (B)(90+x)(40+2x)×58%=90x40
(C)(90+2x)(40+x)×58%=90x40 (D)(90+2x)(40+2x)×58%=90x40
8.关于反比例函数,下列说法中错误的是( )
(A)它的图象分布在一、三象限 (B)它的图象过点(-1,-3)
(C)当x>0时,y的值随x的增大两增大 (D)当x<0时,y的值随x的增大而减小
9.下列四个命题中假命题是( )
(A)对角线互相垂直的平行四边形是菱形
(B)对角线相等的平行四边形是矩形
(C)对角线互相垂直平分且相等的四边形是正方形
(D)对角线相等的四边形是平行四边形
10.在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过
C点作CEBD于E,延长AF、EC交于点H,下列结
论中:① AF=FH;②80=BF;③CA=C8;④ BE=3ED;
正确的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
得分
第Ⅱ卷 非选择题(共90分)
二、填空题:(每小题3分,共计30分)
11. 在函数中,自变量x的取值范围是________.
12.计算:_______.
13.一轮船以l6海里/时的速度从港口A出发沿着北偏东60°的方向航行,另一轮船以l2海里/时的速度同时从港口A出发沿着南偏东30°方向航行,离开港口2小时后两船相距_______ 海里.
14.已知关于x的方程的两个根分别是a和b,则a+b=__________.
15.如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB等于 _________ .
16.利用一面墙(墙的长度为12m),其它三面用40m长的篱笆,围成—个面积为l50㎡的长
方形的场地,则此长方形的场地的长为 __________m.(规定长要大于宽)
17.如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连接BD,过点A作BD的垂线,
交BC于E,若EC=3cm,CD= 4cm,则梯形ABCD的面积是_________cm
18.如图所示,将—些相同的棋子按如图所示的规律摆放:第l个图形有4个棋子,第2个图
形有8个棋子,第3个图形有l2个棋子,第四个图形有l6个棋子……,依此规律,第lO
个图形有_________个棋子.
19.菱形ABCD中,∠A=60°,AB=6,点P是菱形内一点,PB=PD=,则AP的长为_____.
20.如图,正方形ABCD的面积为l2,△ABE是等边三角形,点E在正方形ABCD内,在
对角线AC上有一点P,PD+PE的和最小,则这个最小值为_______.
三、解答题:(21~24题每题各6分,25、26题每题各8分,27、28题每题各10分,共计60分)
得分
21.(本题6分)
计算(1) (2)
得分
22.(本题6分)
解下列一元二次方程
(1) (2)
得分
23.(本题6分)
图1,图2均为正方形网格,每个小正方形的边长均为l,各个小正方形的顶点叫做格点,
请在下面的网格中按要求分别画图,使得每个图形的顶点均在格点上.
(1)画一个直角三角形,且三边长为,2,5;
(2)画一个边长为整数的等腰三角形,且面积等于l2.
得分
24.(本题6分)
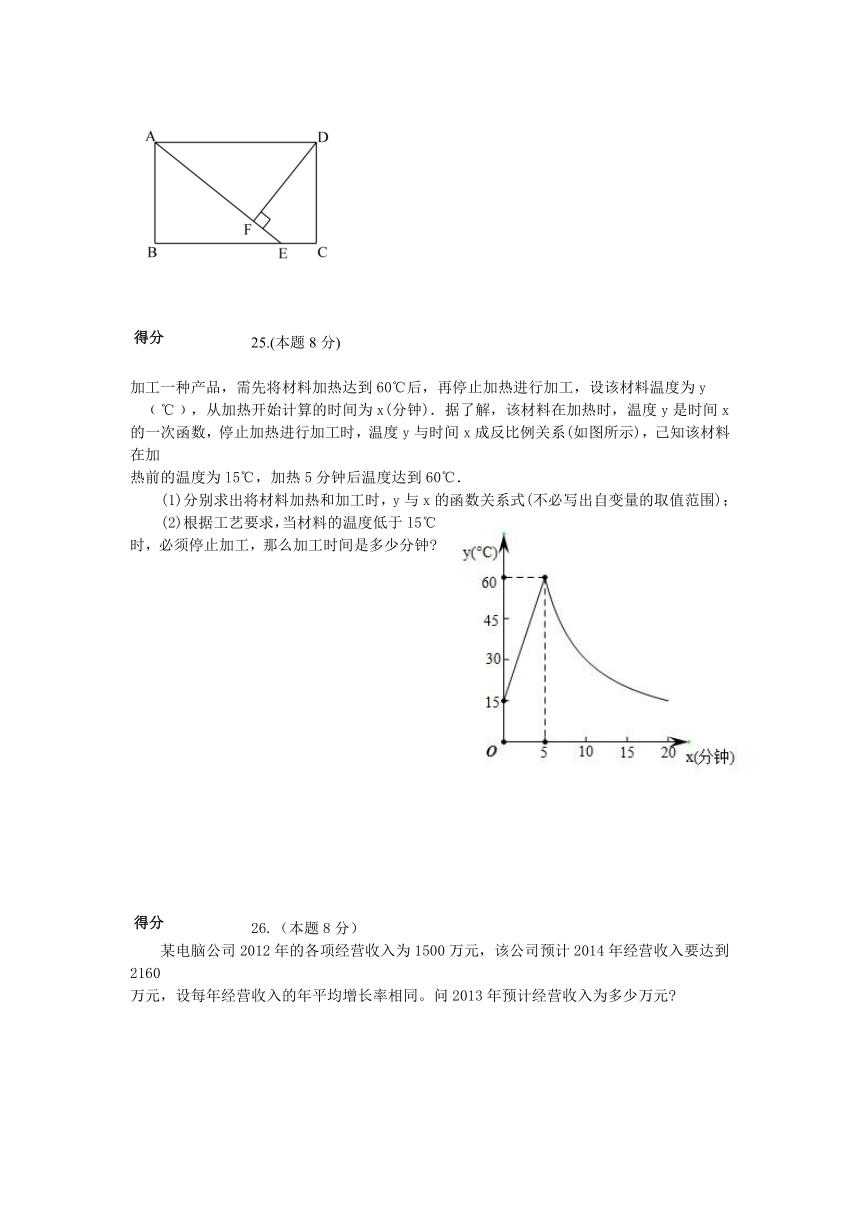
已知如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F.
求证:DF=DC.
得分
25.(本题8分)
加工一种产品,需先将材料加热达到60℃后,再停止加热进行加工,设该材料温度为y
﹙℃﹚,从加热开始计算的时间为x(分钟).据了解,该材料在加热时,温度y是时间x的一次函数,停止加热进行加工时,温度y与时间x成反比例关系(如图所示),己知该材料在加
热前的温度为l5℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和加工时,y与x的函数关系式(不必写出自变量的取值范围);
(2)根据工艺要求,当材料的温度低于l5℃时,必须停止加工,那么加工时间是多少分钟
得分
26.(本题8分)
某电脑公司2012年的各项经营收入为1500万元,该公司预计2014年经营收入要达到2160
万元,设每年经营收入的年平均增长率相同。问2013年预计经营收入为多少万元
得分
27.(本题10分)
如图,在平面直角坐标系中,点0为坐标原点,直线交x轴于点A,交y轴
于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
(1)求直线BD的解析式:
(2)过C作CH∥y轴交直线AB于点H,点P是射线CH上的一个动点,过点P作PE⊥CH,直线PE交直线BD于E、交直线BC于F,设线段EF的长为d(d≠0),点P的纵坐标为t,求d与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,取线段AB的中点M,y轴上有一点N.试问:是否存在这样的t的值,使四边形PEMN是平行四边形,若存在,请求出t的值;若不存在,请说明理由.
得分
28.(本题10分)
在四边形ABCD中,AD∥BC,AD=CD,点E在DC的延长线上,AE交BC边于点F,
且AE=AB.
(1)如图l,求证:∠B=∠E:
(2)如图2,在(1)的条件下,在BC上取一点M,使BM=CE,连接AM,过M作
MH⊥AE于H,连接CH,若∠BAE=∠EHC=60°,CF=2,求线段AH的长.
香坊区2012-2013学年度下学期
八年级数学期末调研测试参考答案及评分标准
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
选项 B B B A D C D C D C
二、填空题:
11.; 12.15; 13.40; 14.8; 15.22.5°;
16.15; 17.26; 18.40; 19.或; 20..
三、解答题:
21. (1) (2)
=…………2分 =…………2分
= …………1分 =…………1分
22.(1) (2)
△= …………1分
∴…………1分 ∴或
∴…1分 …1分 ∴…1分 …1分
23.
每个图形3分,如果有其他情况只要画对即可给分.
24.证明:∵四边形ABCD是矩形
∴AD//BC ∠B=90° AB=CD………………1分
∴∠DAF=∠AEB………………1分
∵DF⊥AE
∴∠DFA=∠B=90°………………1分
∴△DFA≌△ABE………………1分
∴DF=AB ………………1分
∴DF=CD………………1分
25.(1)当材料在加热时,
∵温度是时间的一次函数
∴设一次函数的解析式为
有图象可知,一次函数图象经过(0,15),(5,60)
代入可得: ………………1分 解得:………………1分
∴………………1分
当停止加热进行加工时,
∵温度与时间成反比例关系
∴设反比例函数的解析式为
有图象可知,反比例函数图象经过(5,60)
代入可得: 解得:………………2分
∴………………1分
(2)当时, ∴………………1分
∴加工时间为:分钟………………1分
答:加工时间是15分钟.
26. 解:设每年经营收入的平均增长率为。………………1分
………………3分
解得: ………………1分
(不合题意舍去)………………1分
∴1500×(1+20%)=1800(万元)………………2分
答:2013年预计经营中收入为1800万元。
27.(1)当时 则有 ∴A(-8,0) ∴AO=8
当时 则有 ∴B(0,6) ∴OB=6
在Rt△AOB中 则有AB=10
过点D作DG⊥AB于点G
∵BD平分∠ABO OB⊥OA ∴OD=DG
设OD=DG=
∵
∴
即:
∴ ∴D(-3,0)………………1分
设直线BD的解析式为
将B(0,6),D(-3,0)代入得:
解得:
∴直线BD的解析式为………………1分
(2)∵AC=AB=10 OA=8
∴OC=10-8=2
∴C(2,0)
设直线BC的解析式为
将B(0,6),C(2,0)代入
解得:
∴直线BC的解析式为
∵CH//轴 点P的纵坐标为
∴当时 则有 ∴
∴
∴E(,) F(,)………………2分
①当0≤<6时,EF= ∴………………1分
②当>6时,EF= ∴………………1分
(3)由点M为线段AB的中点
易求:M(-4,3)………………1分
∴MN=4
∵四边形PEMN是平行四边形
∴MN//PE MN=PE=4
由(2)得:E(,),P(2,)………………1分
∴PE==4 ………………1分
解得:=2………………1分
∴存在这样的=2,使得四边形PEMN是平行四边形.
28. (1)过点A作AG//CD交BC于点G,AP⊥BC于点P,AQ⊥CD于点Q,连接AC.
则有∠APG=∠AQE=90°………………1分
∵AD//BC
∴四边形AGCD是平行四边形
∵AD=CD………………1分
∴□AGCD是菱形
∴∠ACP=∠ACD ∴AP=AQ………………1分
∵AB=AE
∴Rt△APB≌Rt△AQE………………1分
∴∠B=∠E………………1分
(2)在HE上截取HK=CH,连接MK,AC.
∵∠KHC=60°
∴△KHC是等边三角形 ∠AHC=120°
∴CH=CK ∠HKC=60°
∵AB=AE ∠B=∠E BM=CE
∴△ABM≌△AEC………………1分
∴∠BAM=∠EAC AM=AC
∵∠BAE=60°
∴∠MAC=60°
∴△AMC是等边三角形
∴AC=CM ∠HCK=∠ACM=60°
∴∠MCK=∠ACH
∴△MCK≌△ACH………………1分
∴MK=AH ∠AHC=∠MKC=120°
∴∠MKF=120°-60°=60°
∵MH⊥AH
∴∠HMK=30°
∴设CH=CK=HK=
在Rt△MHK中,则有MK=AH=
在Rt△MHK中
∴MH=
利用面积法易求:MF=4………………1分
∴AM=MC=4+2=6
在Rt△AHM中
∴………………1分
解得: (舍去)
∴AH=2=………………1分
图①
图②
八年级数学试卷
考生须知:本试卷分为第Ⅰ卷和第Ⅱ卷两部分. 第Ⅰ卷为选择题,满分为30分;第Ⅱ卷为填空题和选择题,满分为90分.本试卷共28道题,满分120分,考试时间为120分钟.
题号 一 二 三 总分
得分 21 22 23 24 25 26 27 28
得分
第Ⅰ卷 选择题(共30分)
一、单项选择题(每小题3分,共30分)
1.下列各式中最简二次根式为( )
(A) (B) (C) (D)
2.如果x=-3是方程的一个根,那么m的值是( )
(A)一4 (B)4 (C)3 (D)-3
3.下列计算正确的是( )
(A) (B) (C) (D)
4.关于x的一元二次方程的根的情况是( )
(A)方程没有实数根 (B)方程有两个相等的实数根
(C)方程有两个不相等的实数根 (D)以上答案都不对
5.将方程化成的形式是( )
(A) (B)
(C) (D)
6.如图所示,□ABCD的周长为l6cm,对角线AC与BD相
交于点O,交AD于E,连接CE,则ADCE的
周长为( )
(A)4cm (B)6cm (C)8cm (D)10cm
7.在一幅长90cm,宽40cm的风景画的四周的外边镶宽度相同的金色纸边,制成一幅挂图,
使风景画的面积是整个挂图面积的58%,设金色纸边的宽度为xcm,则可列方程为( )
(A)(90+x)(40+x)×58%=90x40 (B)(90+x)(40+2x)×58%=90x40
(C)(90+2x)(40+x)×58%=90x40 (D)(90+2x)(40+2x)×58%=90x40
8.关于反比例函数,下列说法中错误的是( )
(A)它的图象分布在一、三象限 (B)它的图象过点(-1,-3)
(C)当x>0时,y的值随x的增大两增大 (D)当x<0时,y的值随x的增大而减小
9.下列四个命题中假命题是( )
(A)对角线互相垂直的平行四边形是菱形
(B)对角线相等的平行四边形是矩形
(C)对角线互相垂直平分且相等的四边形是正方形
(D)对角线相等的四边形是平行四边形
10.在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过
C点作CEBD于E,延长AF、EC交于点H,下列结
论中:① AF=FH;②80=BF;③CA=C8;④ BE=3ED;
正确的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
得分
第Ⅱ卷 非选择题(共90分)
二、填空题:(每小题3分,共计30分)
11. 在函数中,自变量x的取值范围是________.
12.计算:_______.
13.一轮船以l6海里/时的速度从港口A出发沿着北偏东60°的方向航行,另一轮船以l2海里/时的速度同时从港口A出发沿着南偏东30°方向航行,离开港口2小时后两船相距_______ 海里.
14.已知关于x的方程的两个根分别是a和b,则a+b=__________.
15.如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB等于 _________ .
16.利用一面墙(墙的长度为12m),其它三面用40m长的篱笆,围成—个面积为l50㎡的长
方形的场地,则此长方形的场地的长为 __________m.(规定长要大于宽)
17.如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连接BD,过点A作BD的垂线,
交BC于E,若EC=3cm,CD= 4cm,则梯形ABCD的面积是_________cm
18.如图所示,将—些相同的棋子按如图所示的规律摆放:第l个图形有4个棋子,第2个图
形有8个棋子,第3个图形有l2个棋子,第四个图形有l6个棋子……,依此规律,第lO
个图形有_________个棋子.
19.菱形ABCD中,∠A=60°,AB=6,点P是菱形内一点,PB=PD=,则AP的长为_____.
20.如图,正方形ABCD的面积为l2,△ABE是等边三角形,点E在正方形ABCD内,在
对角线AC上有一点P,PD+PE的和最小,则这个最小值为_______.
三、解答题:(21~24题每题各6分,25、26题每题各8分,27、28题每题各10分,共计60分)
得分
21.(本题6分)
计算(1) (2)
得分
22.(本题6分)
解下列一元二次方程
(1) (2)
得分
23.(本题6分)
图1,图2均为正方形网格,每个小正方形的边长均为l,各个小正方形的顶点叫做格点,
请在下面的网格中按要求分别画图,使得每个图形的顶点均在格点上.
(1)画一个直角三角形,且三边长为,2,5;
(2)画一个边长为整数的等腰三角形,且面积等于l2.
得分
24.(本题6分)
已知如图,矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE于F.
求证:DF=DC.
得分
25.(本题8分)
加工一种产品,需先将材料加热达到60℃后,再停止加热进行加工,设该材料温度为y
﹙℃﹚,从加热开始计算的时间为x(分钟).据了解,该材料在加热时,温度y是时间x的一次函数,停止加热进行加工时,温度y与时间x成反比例关系(如图所示),己知该材料在加
热前的温度为l5℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和加工时,y与x的函数关系式(不必写出自变量的取值范围);
(2)根据工艺要求,当材料的温度低于l5℃时,必须停止加工,那么加工时间是多少分钟
得分
26.(本题8分)
某电脑公司2012年的各项经营收入为1500万元,该公司预计2014年经营收入要达到2160
万元,设每年经营收入的年平均增长率相同。问2013年预计经营收入为多少万元
得分
27.(本题10分)
如图,在平面直角坐标系中,点0为坐标原点,直线交x轴于点A,交y轴
于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
(1)求直线BD的解析式:
(2)过C作CH∥y轴交直线AB于点H,点P是射线CH上的一个动点,过点P作PE⊥CH,直线PE交直线BD于E、交直线BC于F,设线段EF的长为d(d≠0),点P的纵坐标为t,求d与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,取线段AB的中点M,y轴上有一点N.试问:是否存在这样的t的值,使四边形PEMN是平行四边形,若存在,请求出t的值;若不存在,请说明理由.
得分
28.(本题10分)
在四边形ABCD中,AD∥BC,AD=CD,点E在DC的延长线上,AE交BC边于点F,
且AE=AB.
(1)如图l,求证:∠B=∠E:
(2)如图2,在(1)的条件下,在BC上取一点M,使BM=CE,连接AM,过M作
MH⊥AE于H,连接CH,若∠BAE=∠EHC=60°,CF=2,求线段AH的长.
香坊区2012-2013学年度下学期
八年级数学期末调研测试参考答案及评分标准
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
选项 B B B A D C D C D C
二、填空题:
11.; 12.15; 13.40; 14.8; 15.22.5°;
16.15; 17.26; 18.40; 19.或; 20..
三、解答题:
21. (1) (2)
=…………2分 =…………2分
= …………1分 =…………1分
22.(1) (2)
△= …………1分
∴…………1分 ∴或
∴…1分 …1分 ∴…1分 …1分
23.
每个图形3分,如果有其他情况只要画对即可给分.
24.证明:∵四边形ABCD是矩形
∴AD//BC ∠B=90° AB=CD………………1分
∴∠DAF=∠AEB………………1分
∵DF⊥AE
∴∠DFA=∠B=90°………………1分
∴△DFA≌△ABE………………1分
∴DF=AB ………………1分
∴DF=CD………………1分
25.(1)当材料在加热时,
∵温度是时间的一次函数
∴设一次函数的解析式为
有图象可知,一次函数图象经过(0,15),(5,60)
代入可得: ………………1分 解得:………………1分
∴………………1分
当停止加热进行加工时,
∵温度与时间成反比例关系
∴设反比例函数的解析式为
有图象可知,反比例函数图象经过(5,60)
代入可得: 解得:………………2分
∴………………1分
(2)当时, ∴………………1分
∴加工时间为:分钟………………1分
答:加工时间是15分钟.
26. 解:设每年经营收入的平均增长率为。………………1分
………………3分
解得: ………………1分
(不合题意舍去)………………1分
∴1500×(1+20%)=1800(万元)………………2分
答:2013年预计经营中收入为1800万元。
27.(1)当时 则有 ∴A(-8,0) ∴AO=8
当时 则有 ∴B(0,6) ∴OB=6
在Rt△AOB中 则有AB=10
过点D作DG⊥AB于点G
∵BD平分∠ABO OB⊥OA ∴OD=DG
设OD=DG=
∵
∴
即:
∴ ∴D(-3,0)………………1分
设直线BD的解析式为
将B(0,6),D(-3,0)代入得:
解得:
∴直线BD的解析式为………………1分
(2)∵AC=AB=10 OA=8
∴OC=10-8=2
∴C(2,0)
设直线BC的解析式为
将B(0,6),C(2,0)代入
解得:
∴直线BC的解析式为
∵CH//轴 点P的纵坐标为
∴当时 则有 ∴
∴
∴E(,) F(,)………………2分
①当0≤<6时,EF= ∴………………1分
②当>6时,EF= ∴………………1分
(3)由点M为线段AB的中点
易求:M(-4,3)………………1分
∴MN=4
∵四边形PEMN是平行四边形
∴MN//PE MN=PE=4
由(2)得:E(,),P(2,)………………1分
∴PE==4 ………………1分
解得:=2………………1分
∴存在这样的=2,使得四边形PEMN是平行四边形.
28. (1)过点A作AG//CD交BC于点G,AP⊥BC于点P,AQ⊥CD于点Q,连接AC.
则有∠APG=∠AQE=90°………………1分
∵AD//BC
∴四边形AGCD是平行四边形
∵AD=CD………………1分
∴□AGCD是菱形
∴∠ACP=∠ACD ∴AP=AQ………………1分
∵AB=AE
∴Rt△APB≌Rt△AQE………………1分
∴∠B=∠E………………1分
(2)在HE上截取HK=CH,连接MK,AC.
∵∠KHC=60°
∴△KHC是等边三角形 ∠AHC=120°
∴CH=CK ∠HKC=60°
∵AB=AE ∠B=∠E BM=CE
∴△ABM≌△AEC………………1分
∴∠BAM=∠EAC AM=AC
∵∠BAE=60°
∴∠MAC=60°
∴△AMC是等边三角形
∴AC=CM ∠HCK=∠ACM=60°
∴∠MCK=∠ACH
∴△MCK≌△ACH………………1分
∴MK=AH ∠AHC=∠MKC=120°
∴∠MKF=120°-60°=60°
∵MH⊥AH
∴∠HMK=30°
∴设CH=CK=HK=
在Rt△MHK中,则有MK=AH=
在Rt△MHK中
∴MH=
利用面积法易求:MF=4………………1分
∴AM=MC=4+2=6
在Rt△AHM中
∴………………1分
解得: (舍去)
∴AH=2=………………1分
图①
图②
同课章节目录
